Похожие презентации:
Аналитическое задание многогранников
1. Аналитическое задание многогранников
Неравенства ax + by + cz + d 0 и ax + by + cz + d 0определяют полупространства, на которые плоскость, заданная
уравнением ax + by + cz + d = 0, разбивает пространство.
Если грани выпуклого многогранника лежат в плоскостях,
задаваемых уравнениями
a1x + b1y + c1z + d1 = 0,
………………………..,
anx + bny + cnz + dn = 0,
то сам многогранник задается системой неравенств
a1 x b1 y c1 z d1 0,
...............................,
a x b y c z d 0.
n
n
n
n
2. Упражнение 1
Два полупространства задаются неравенствамиa1x + b1y + c1z + d1 0, a2x + b2y + c2z + d2 0. Как
будет задаваться пересечение этих полупространств?
Ответ: Системой этих неравенств.
3. Упражнение 2
Определите, какому полупространству 5x + 3y - z - 2 0 или5x + 3y - z - 2 0 принадлежит точка: а) А(1, 0, 0); б) B(0, 1, 0);
в) C(0, 0, 1).
Ответ: а) Первому; б) первому; в) второму.
4. Упражнение 3
Какой многогранник задается системой неравенств0 x 1,
0 y 1,
0 z 1?
Ответ: Куб.
5. Упражнение 4
Какую фигуру в пространстве задает следующая системанеравенств
0 x 3,
0 y 5,
0 z 4?
Ответ: Прямоугольный параллелепипед.
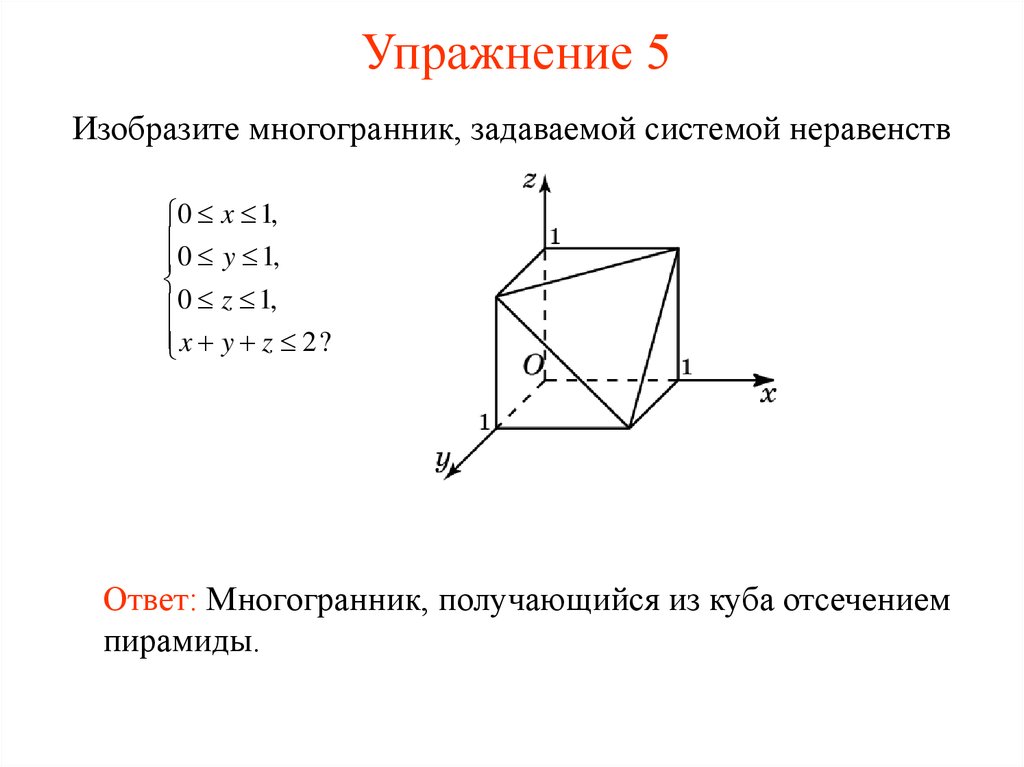
6. Упражнение 5
Изобразите многогранник, задаваемой системой неравенств0 x 1,
0 y 1,
0 z 1,
x y z 2?
Ответ: Многогранник, получающийся из куба отсечением
пирамиды.
7. Упражнение 6
Какой многогранник задается неравенством| x | | y | | z | 1?
Ответ: Октаэдр.
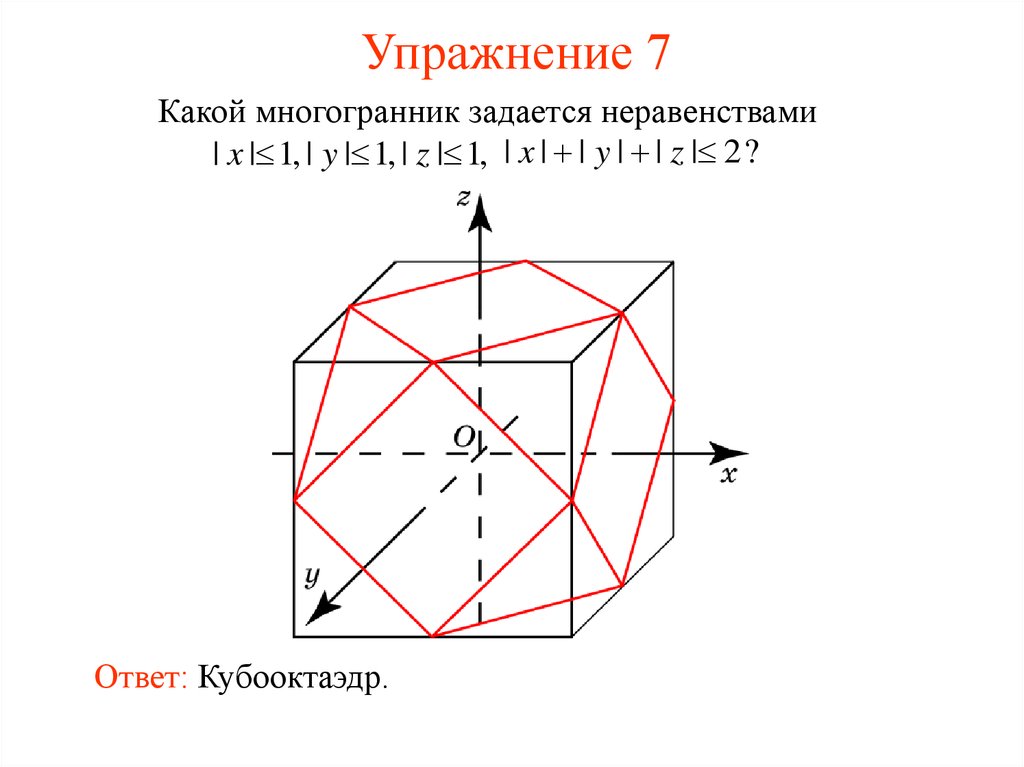
8. Упражнение 7
Какой многогранник задается неравенствами| x | 1, | y | 1, | z | 1, | x | | y | | z | 2?
Ответ: Кубооктаэдр.
9. Упражнение 8
Какие неравенства, задают правильный тетраэдр, вершиныкоторого имеют координаты: (1, 1, -1), (1, -1, 1), (-1, 1, 1), (-1, -1,-1).
Ответ: |x+y|+z 1, |x-y|-z 1.
10. Упражнение 9
Какая фигура в пространстве задается системой неравенств?x2 z 2 R2 ,
0 y h ?
Ответ: Цилиндр.
11. Упражнение 10
Напишите неравенства, определяющие конус с вершиной вточке S(0,0,h) и основание которого - круг радиуса R, лежащий в
плоскости Oxy.
h z 2
) , 0 z h.
Ответ: x y ( R
h
2
2
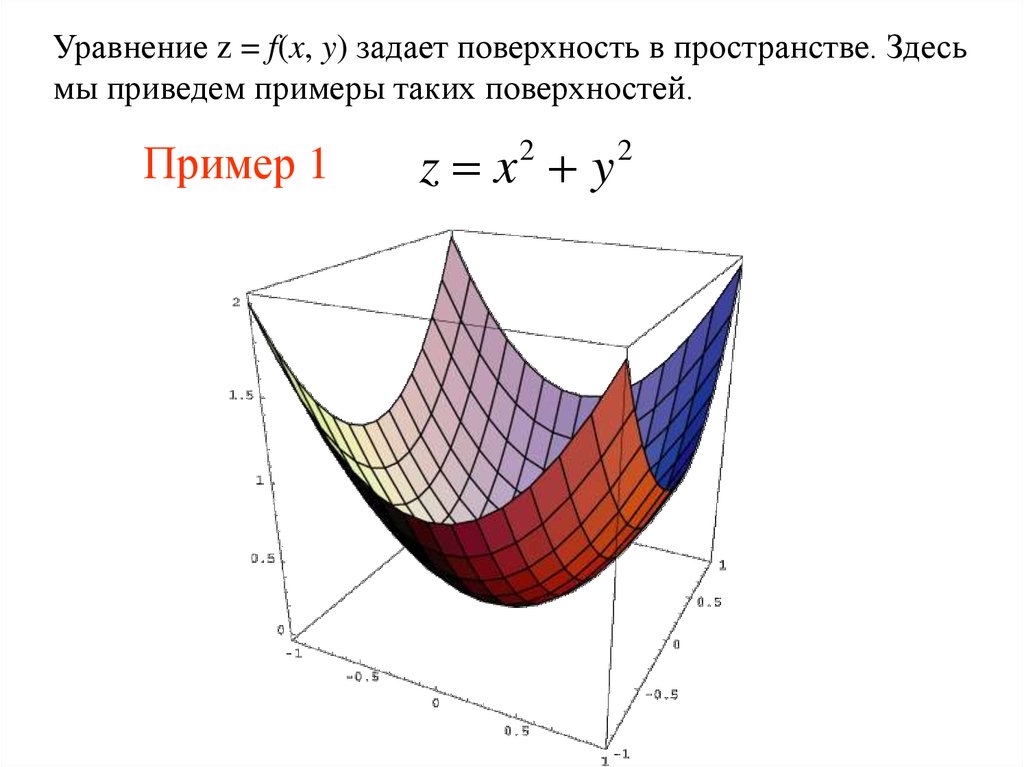
12. Пример 1
Уравнение z = f(x, y) задает поверхность в пространстве. Здесьмы приведем примеры таких поверхностей.
Пример 1
z x y
2
2
13. Пример 2
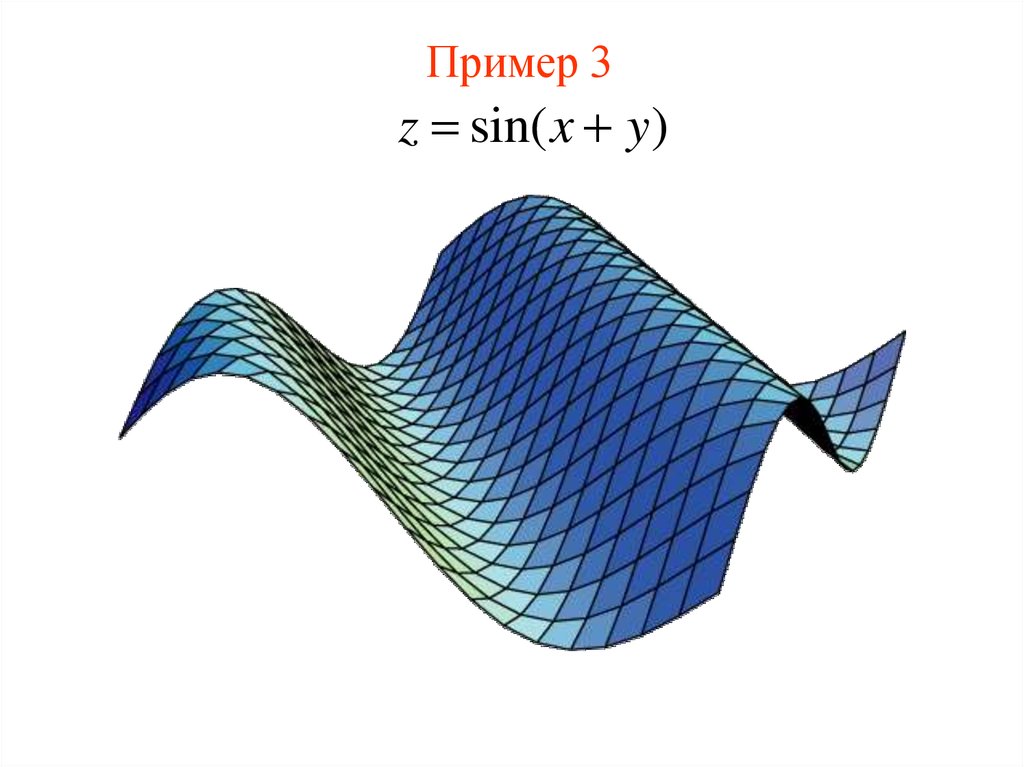
z x y14. Пример 3
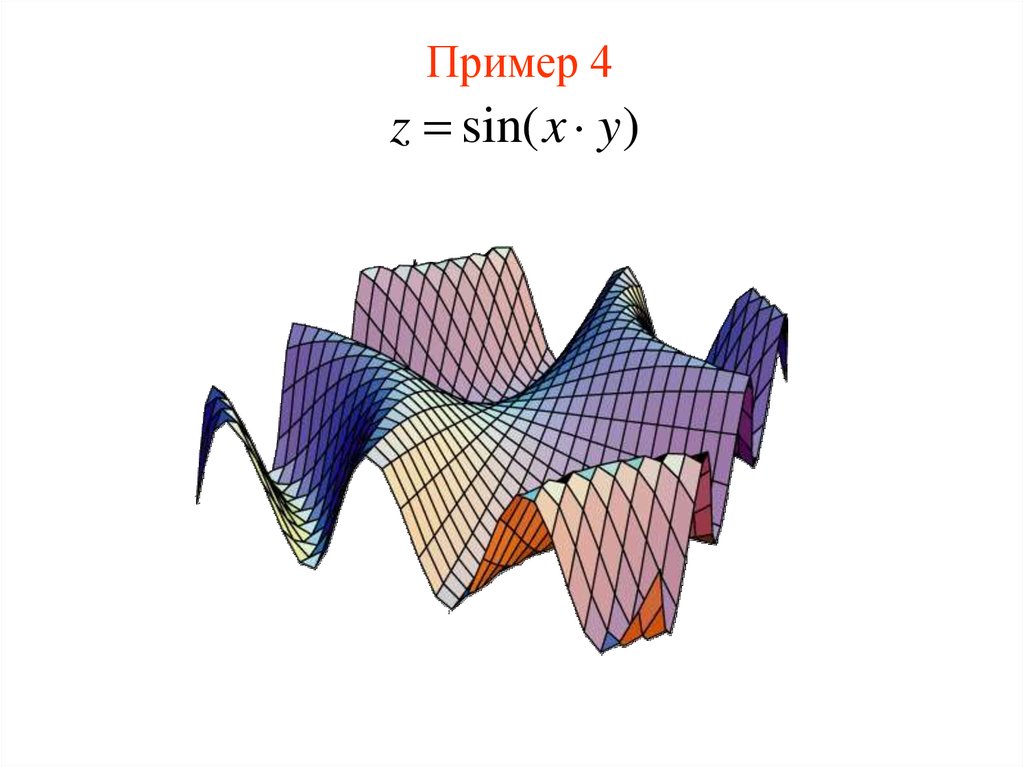
z sin( x y )15. Пример 4
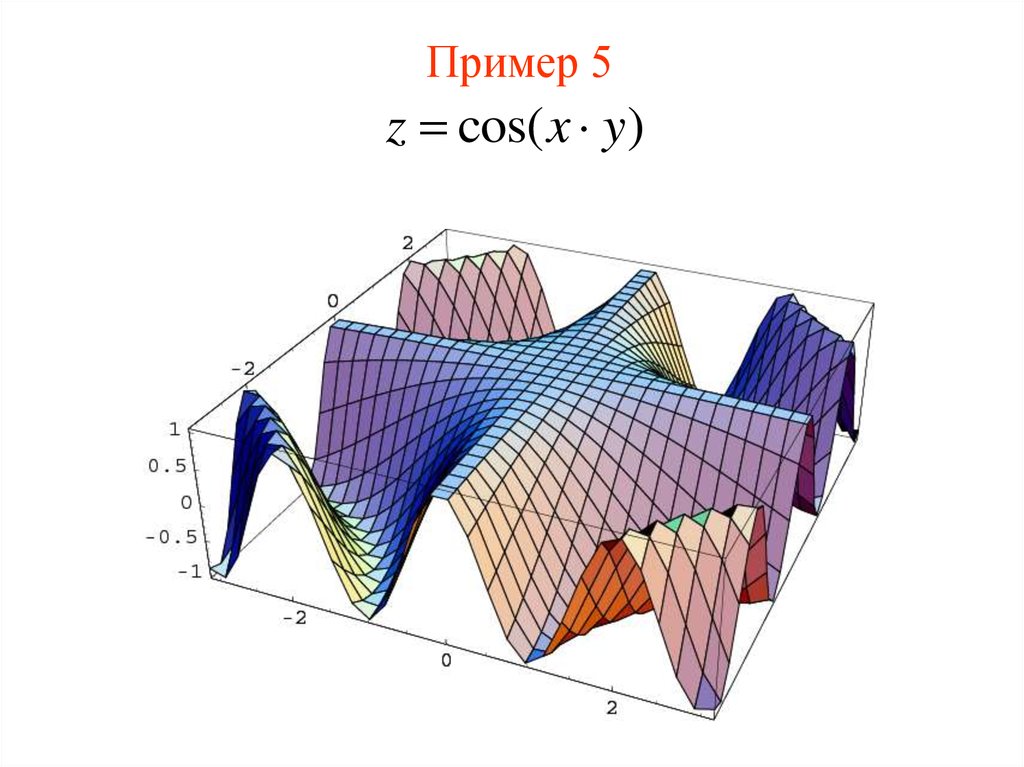
z sin( x y)16. Пример 5
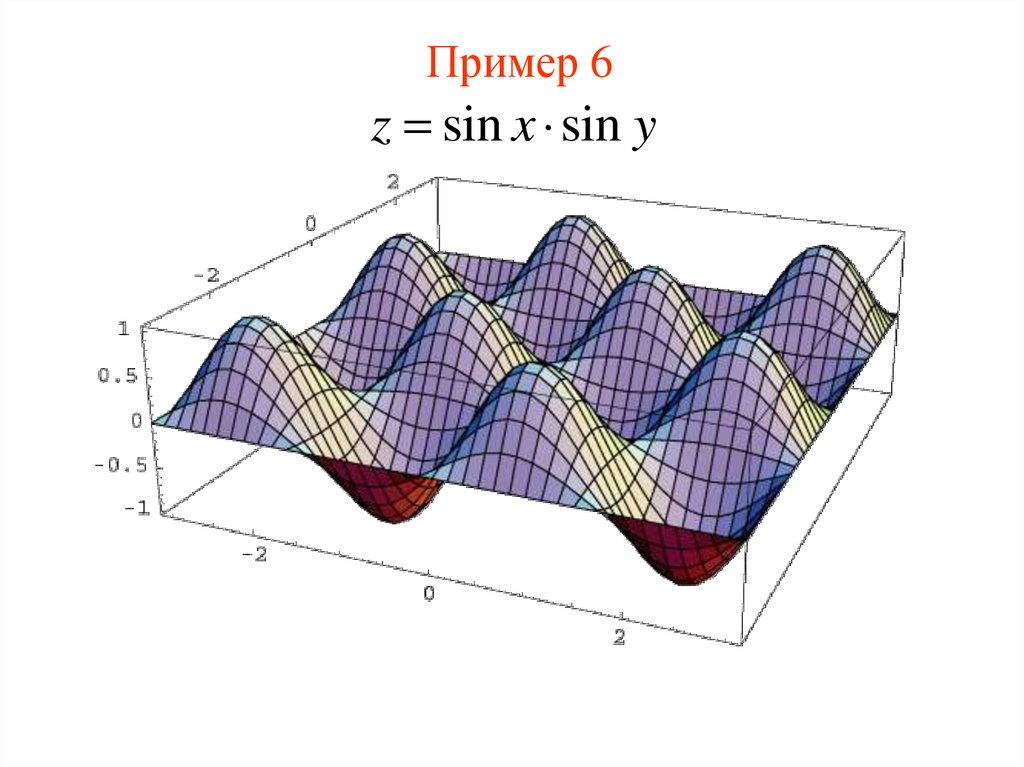
z cos( x y)17. Пример 6
z sin x sin y18. Пример 7
z sin x sin y2
2
19. Пример 8
z sin( x 1) sin( y 1)2
2
20. Упражнение 11
Найдите объем многогранника, координаты (x, y) точеккоторого удовлетворяют системе неравенств
0 x 2,
0 y 3,
0 z 4.
Ответ: 24.
21. Упражнение 12
Найдите объем многогранника, координаты (x, y) точеккоторого удовлетворяют системе неравенств
0 x 4,
0 y ,
0 z ,
2 y 3 z 6.
Ответ: 12.
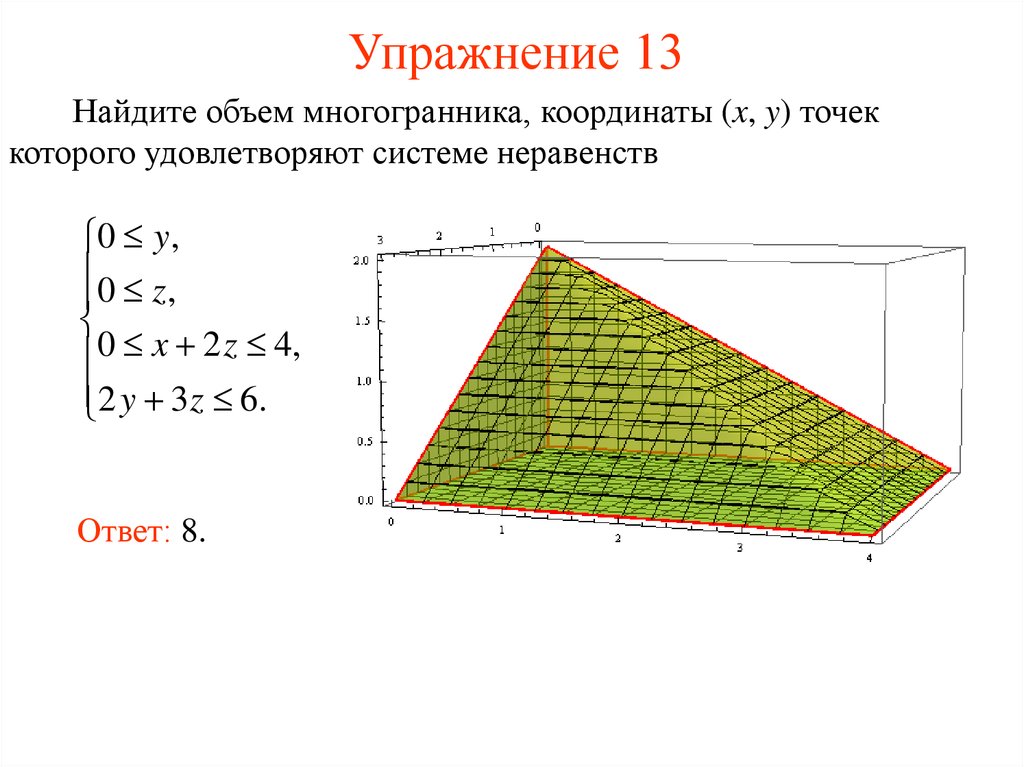
22. Упражнение 13
Найдите объем многогранника, координаты (x, y) точеккоторого удовлетворяют системе неравенств
0 y ,
0 z ,
0 x 2 z 4,
2 y 3 z 6.
Ответ: 8.
23. Упражнение 14
Найдите объем многогранника, координаты (x, y) точеккоторого удовлетворяют системе неравенств
x y z 6,
0 x,
0 y ,
0 z.
Ответ: 36.
24. Упражнение 15
Найдите прямую, проходящую через центр куба, для которойсумма квадратов расстояний от вершин данного куба до этой
прямой: а) максимальна; б) минимальна.
Решение. Пусть вершины куба имеют координаты (1, 1, 1), (-1, 1, 1),
(1, -1, 1), (1, 1, -1), (-1, -1, 1), (-1, 1, -1), (1, -1, -1), (-1, -1, -1) .
Единичный направляющий вектор прямой, проходящей через центр
куба с координатами (0, 0, 0) имеет координаты (x, y, z).
Тогда квадраты расстояний от вершин куба до этой прямой равны
соответственно 3 – (x + y + z)2, 3 – (– x + y + z)2, 3 – (x – y + z)2, 3 –
(x + y – z)2, 3 – (– x – y + z)2, 3 – (– x + y – z)2, 3 – (x – y – z)2, 3 – (– x
– y – z)2.
Возводя в квадрат, складывая и учитывая, что x2 + y2 + z2 =1,
получим, что сумма квадратов расстояний равна 16 и не зависит от
выбора прямой.
















 Математика
Математика








