Механика жидкостей и газов

1. МЕХАНИКА ЖИДКОСТЕЙ И ГАЗОВ

2. Основные понятия МЖГ

Изучает
условия
равновесия
и
закономерности движения текучих сред –
жидкостей и газов.
Допущения:
1. Текучие среды представляем как сплошную
(дискретным,
молекулярным
строением
пренебрегаем).
Следствием
полагаем
рассмотрение свойств в элементарном объеме
dV как в макроскопическом объеме.

3. Основные понятия МЖГ

dM
2. Плотность жидкости (газа)
dV
Если плотность постоянна, среда называется
несжимаемой.
Если плотность переменна, то и среда
сжимаема.
3. Идеальная среда лишена свойства вязкости
(внутреннего трения). Реальная среда
обладает свойствами вязкости (внутреннего
трения).

4.

5. Кинематика газов и жидкостей

w - вектор скорости;
Способ Лагранжа – указывается поведение с
течением времени каждой частицы, составляющей
поток.
Способ Эйлера – устанавливается, что
происходит в каждой точке потока в каждый
момент времени.
Стационарный поток (установившееся движение)
wx wy wz
0

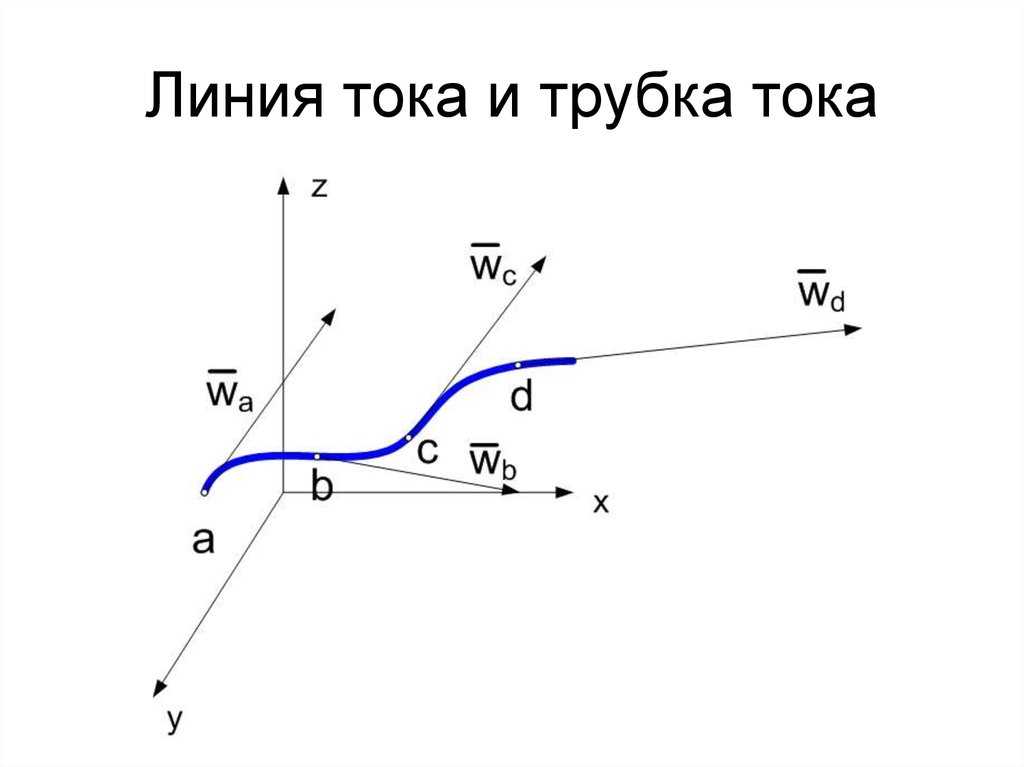
6. Линия тока и трубка тока

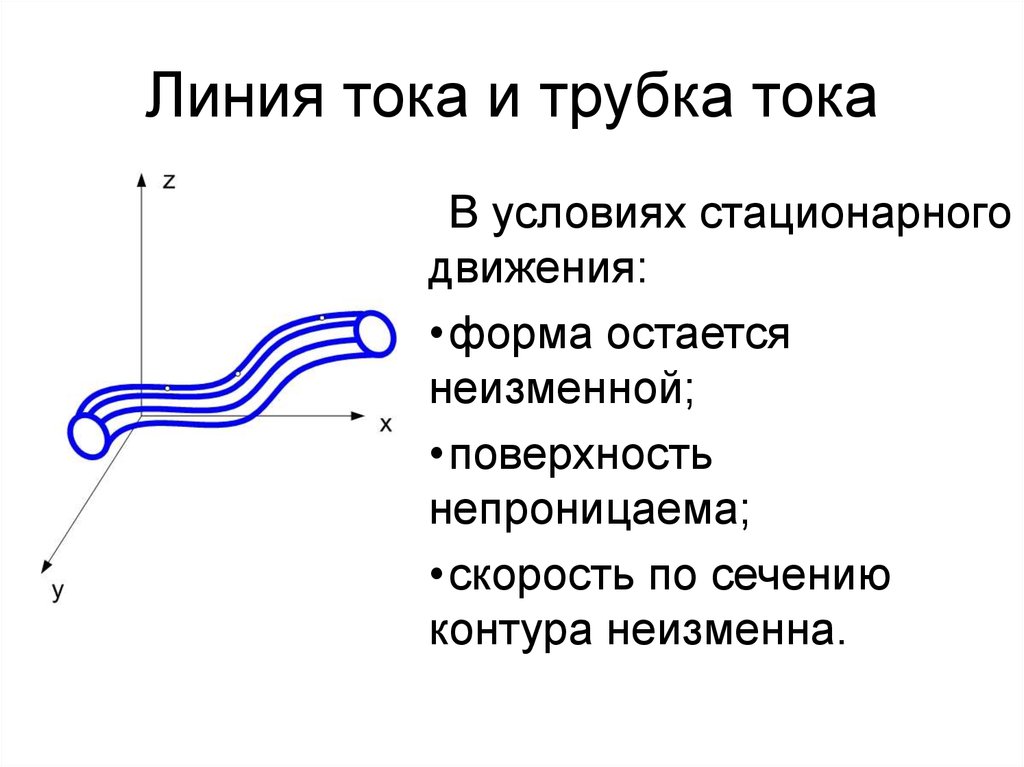
7. Линия тока и трубка тока

В условиях стационарного
движения:
•форма остается
неизменной;
•поверхность
непроницаема;
•скорость по сечению
контура неизменна.

8.

Важнейшая кинематическая
характеристика – вектор скорости. Это и
перемещения материальной точки
dl
w
d
и объем, проходящий через единицу
поверхности в единицу времени
2
dV
w
n
d dF

9.

Вектор плотности потока массы
кг
w [ 2 ]
мс
Представляет массу среды, проходящей
через единицу поверхности ,
расположенную по нормали по отношению к
данному вектору.

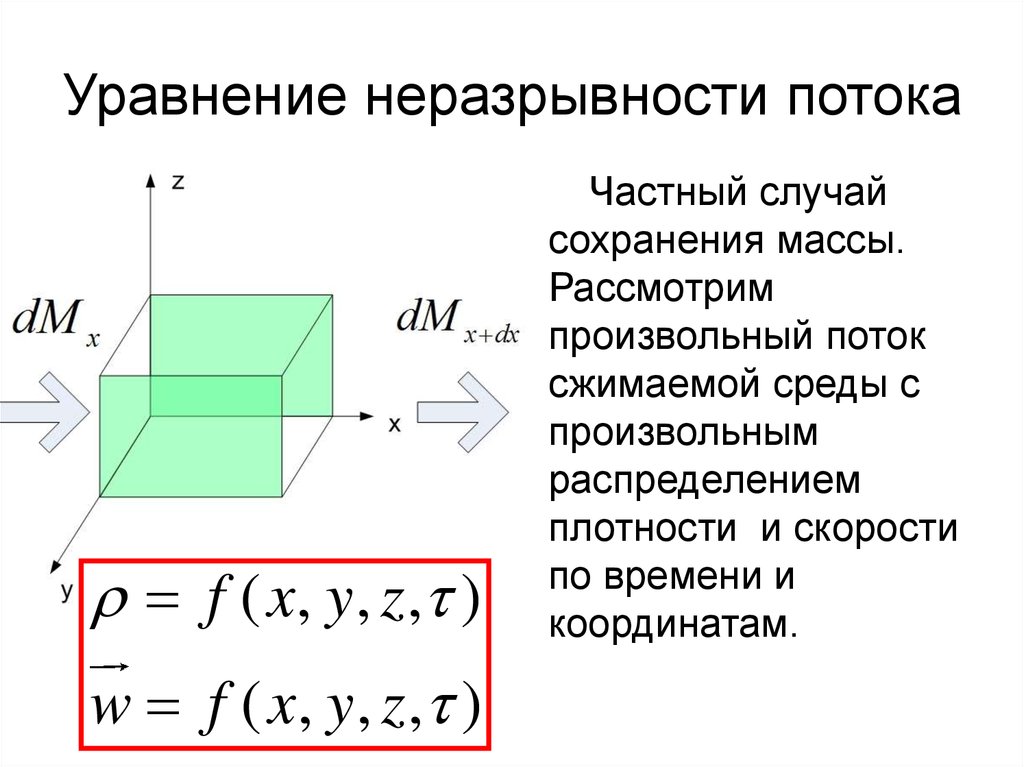
10. Уравнение неразрывности потока

f ( x , y , z , )
w f ( x , y , z , )
Частный случай
сохранения массы.
Рассмотрим
произвольный поток
сжимаемой среды с
произвольным
распределением
плотности и скорости
по времени и
координатам.

11. Уравнение неразрывности потока

Найдем
разность между
dM x wx dydzd
массой вещества,
поступающей в
wx
элементарный
dM x dx ( wx
dx )dydzd
кубик за время dτ,
x
и массой,
покинувшей его
за это же время.
d M x dM x dM x dx
2
( wx )
dVd
x

12. Уравнение неразрывности потока

Для всех осей элементарного кубика:
( wx ) ( w y ) ( wz )
d M
dVd
y
z
x
2
d M dVd
2

13. Уравнение неразрывности потока

В итоге получаем:
( wx ) ( wy ) ( wz )
y
z
x

14. Уравнение неразрывности потока

После упрощения и
интегрирования для
режима стационарного
течения (плоская
задача):
1
w wdF
FF
wF G const
w1 F1 w2 F2 ... const

15. Уравнение изменения давления в движущемся потоке (уравнение Бернулли)

• произвольно
выбираем точку
отсчета;
• произвольно
выбираем сечения;
• определяем
изменение энергии
потока в произвольно
выбранных сечениях.

16. Уравнение изменения давления в движущемся потоке (уравнение Бернулли)

В результате для
идеальной среды
получаем:
рст рдин ргеом const
В результате для
реальной среды
получаем:
рст рдин ргеом рпот const

17. Динамика реальной среды. Режимы движения реальной среды

Движение реальной среды (жидкости и
газа) характеризуется наличием сил
трения, а сама среда – вязкостью.
Выделяют ламинарный, переходный
и турбулентный режимы движения
среды.

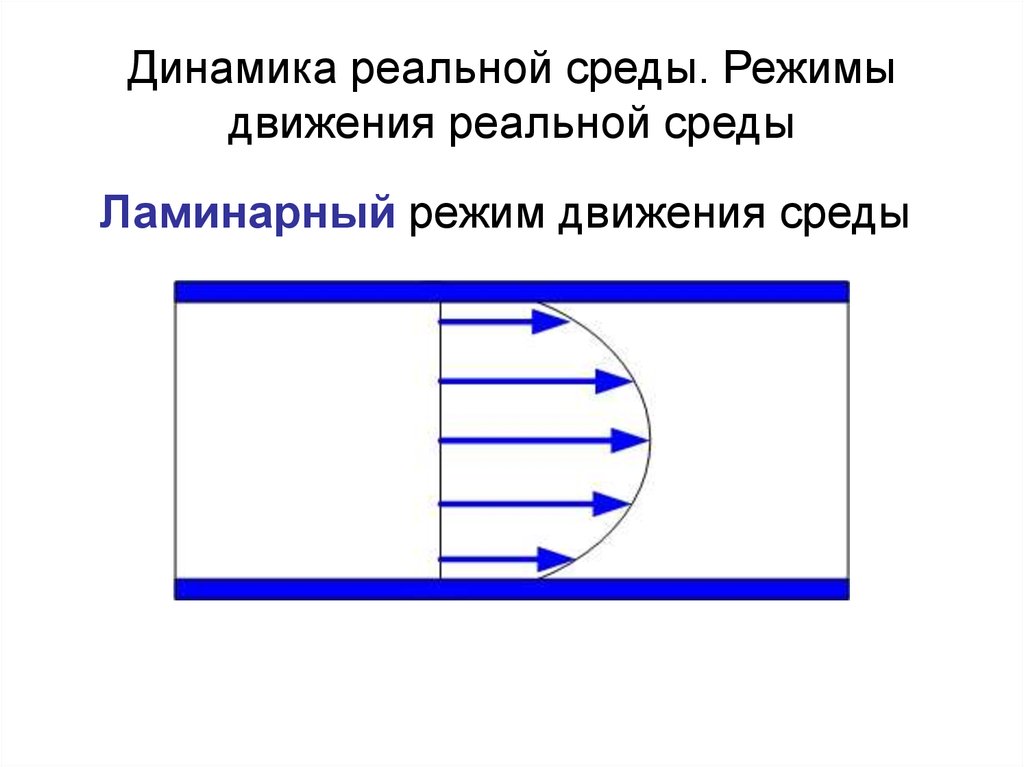
18. Динамика реальной среды. Режимы движения реальной среды

Ламинарный режим движения среды

19. Динамика реальной среды. Режимы движения реальной среды

Переходный режим движения среды

20. Динамика реальной среды. Режимы движения реальной среды

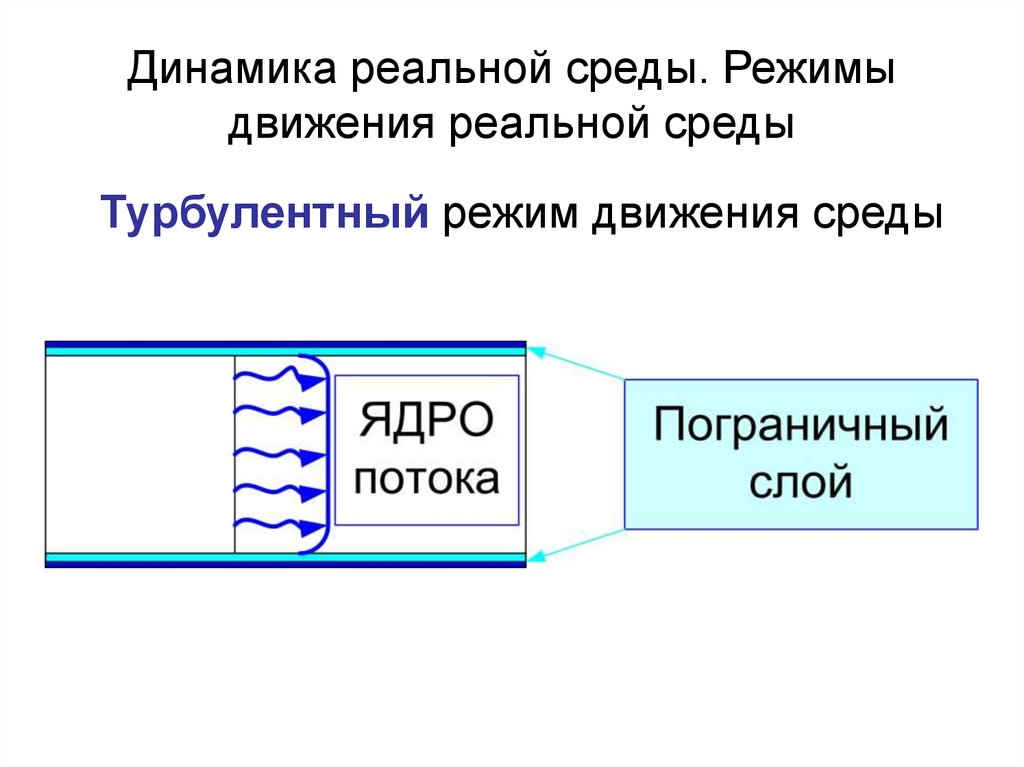
Турбулентный режим движения среды

21. Динамика реальной среды. Режимы движения реальной среды

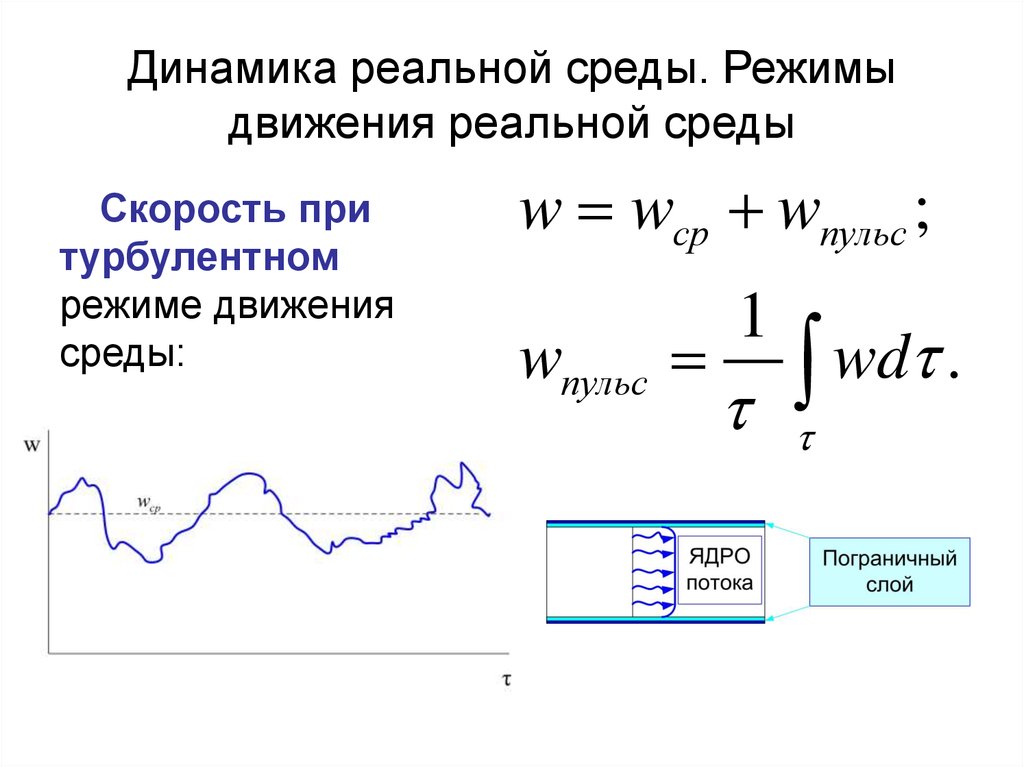
Скорость при
турбулентном
режиме движения
среды:
w wср wпульс ;
wпульс
1
wd
.

22. Динамика реальной среды. Режимы движения реальной среды

Число Рейнольдса
Re
wd
Ламинарный Re<2300
Переходный Re=2300…10000
Развитый турбулентный Re>10000

23. Потери давления на трение и на местных сопротивлениях

Основной расчетной формулой для потерь
напора при турбулентном течении среды
является уже приводившаяся эмпирическая
формула, называемая формулой ВейсбахаДарси и имеющая следующий вид:
2
Lw
Pтр
d 2

24. Потери давления на трение и на местных сопротивлениях

Коэффициент трения
f (Re, )
Относительная шероховатость
/d

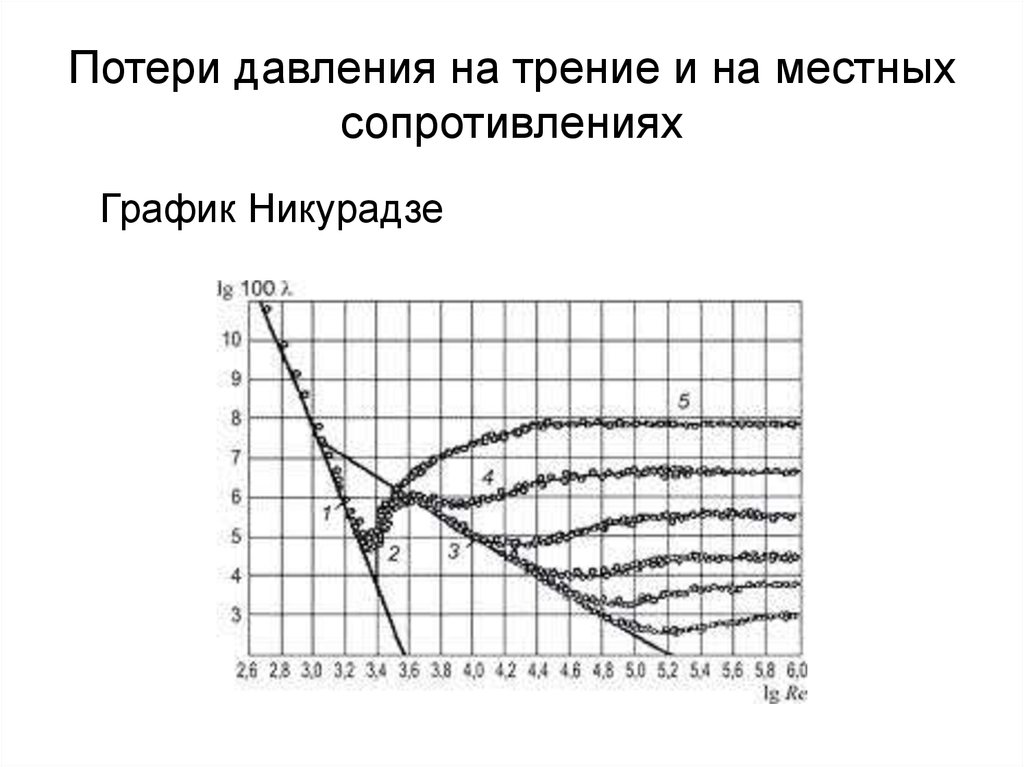
25. Потери давления на трение и на местных сопротивлениях

График Никурадзе

26. Потери давления на трение и на местных сопротивлениях

Потери давления на
местных сопротивлениях
2
w
Pмс
2