Похожие презентации:
Основы гидравлики
1.
Основы гидравлики2.
Гидравлика- наука, изучающая
законы равновесия
и движения жидкостей
Гидростатика
Учение о
равновесии
жидкостей
Гидродинамика
Учение о
движении
жидкостей
3.
Жидкости- физические тела, которые легко изменяют свою форму под
действием приложенных сил.
Для решения задач гидравлики
используют понятие об идеальной
Капельные
Газообразные
жидкости, т.е. жидкости абсолютно
несжимаемой и не обладающей
вязкостью.
характеризуются
малой сжимаемостью и
существенно изменяют свой объем при воздействии
относительно
небольшим
изменением
объема при
сжимающих
сил и изменении
температуры.
изменении температуры.
4.
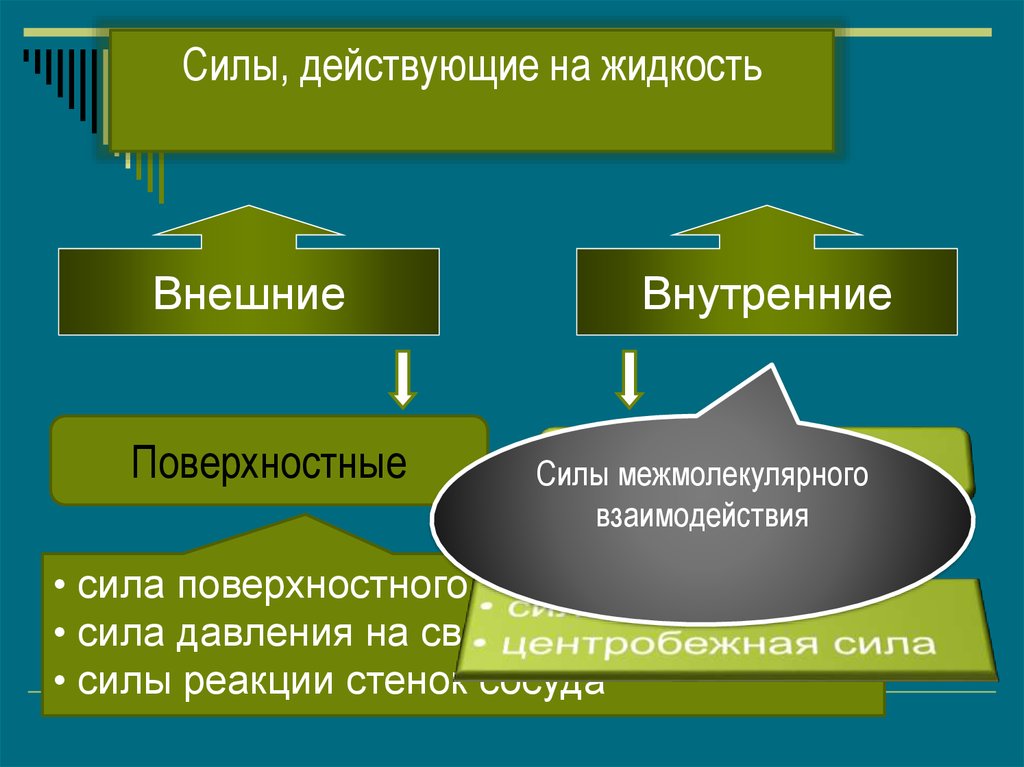
Силы, действующие на жидкостьВнешние
Поверхностные
Внутренние
Силы межмолекулярного
взаимодействия
• сила поверхностного натяжения
• сила давления на свободную поверхность
• силы реакции стенок сосуда
5.
ПлотностьУравнение состояния идеального газа
Сжимаемость
Поверхностное натяжение
Вязкость
Неньютоновские жидкости
Практические задачи
6.
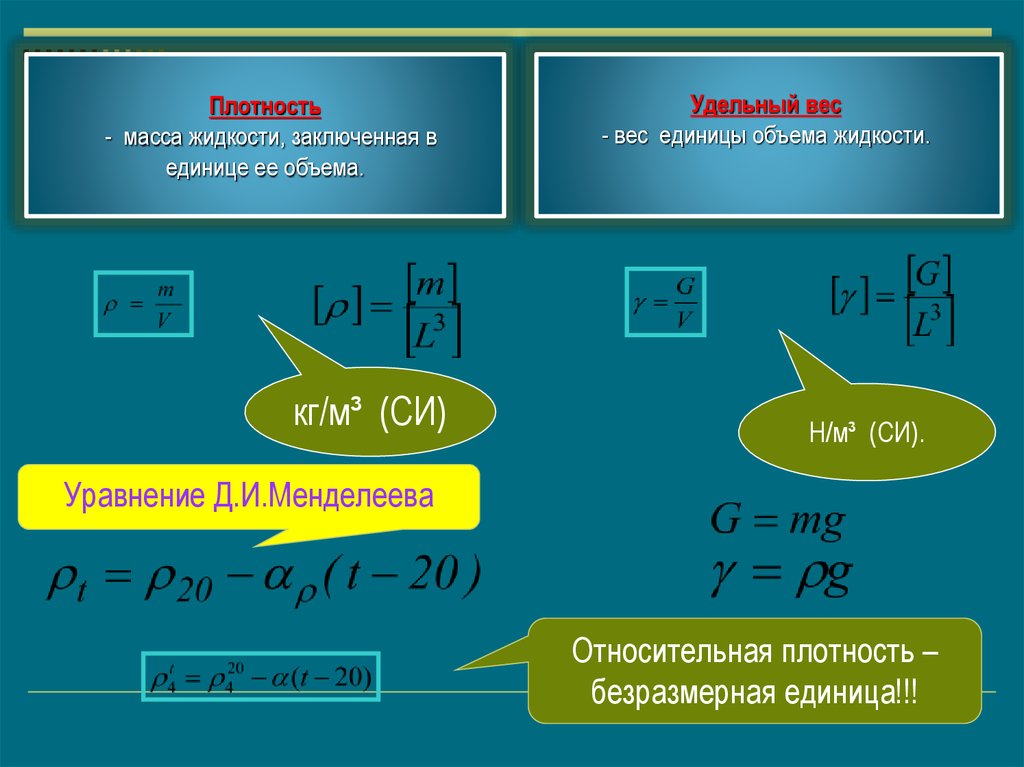
Плотность- масса жидкости, заключенная в
единице ее объема.
кг/м³ (СИ)
Удельный вес
- вес единицы объема жидкости.
Н/м³ (СИ).
Уравнение Д.И.Менделеева
Относительная плотность –
безразмерная единица!!!
7.
Сжимаемостьжидкостей характеризуется коэффициентом
сжимаемости
Модуль упругости
который равен отношению изменения относительного
объема жидкости к изменению давления:
(м2/Н).
Температурное расширение
(град-1)
– величина,
обратная коэффициенту сжимаемости.
Коэффициент сжимаемости и модуль
упругости изменяются в зависимости от
температуры и давления.
Для нефтепродуктов в среднем
для глинистых растворов
В гидравлических расчетах величиной
можно пренебречь, кроме тех случаев,
когда имеет место гидравлический удар.
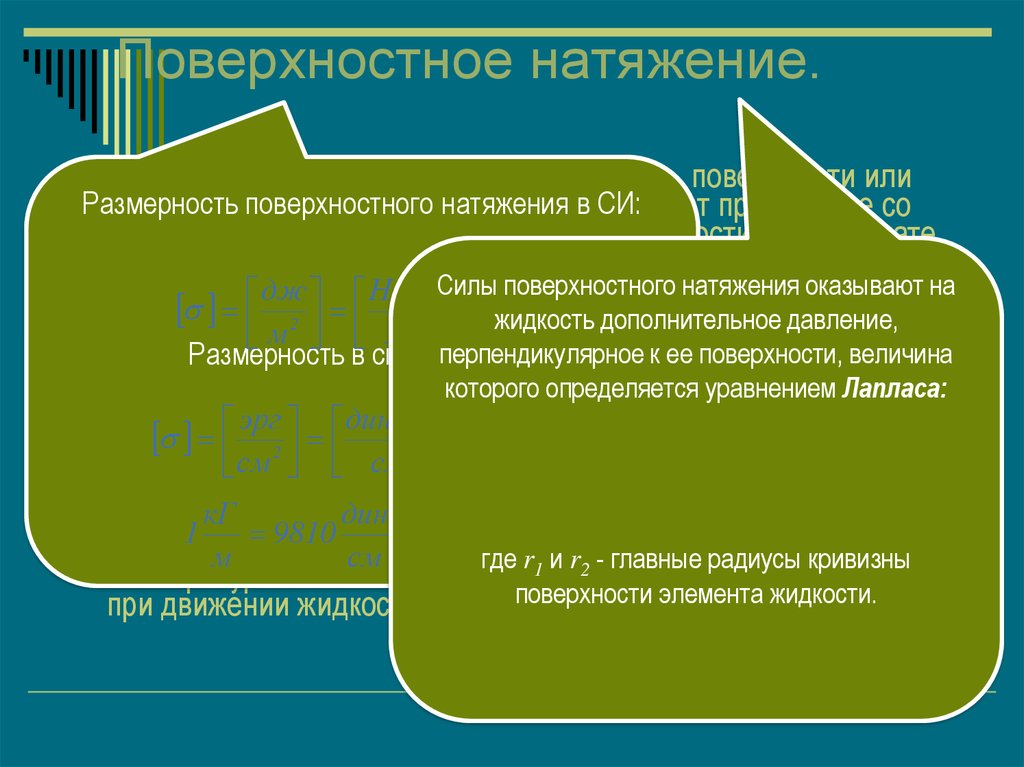
8. Поверхностное натяжение.
Молекулы жидкости, расположенные на ее поверхности илиРазмерность
поверхностного
натяжения
в СИ:
непосредственно
у поверхности,
испытывают
притяжение со
стороны молекул, находящихся внутри жидкости, в результате
чего возникает давление, направленное внутрь жидкости
поверхностного
натяжения оказывают на
дж ее
Нповерхности.
м Силы
Н
перпендикулярно
2 2 жидкость
дополнительное
давление,
Действие этих
жидкости
м м в стремлении
м сил
проявляется
перпендикулярное
к ееновой
поверхности,
величина
Размерность
в системе
СГС:
уменьшить
свою поверхность;
на создание
поверхности
требуется затратить некоторую
которогоработу.
определяется уравнением Лапласа:
см динжидкости
эрг дин
Поверхностным
натяжением
σ называют
работу, которую
для образования
см
см 2 надо
см 2 затратить
единицы новой поверхности жидкости при постоянной
температуре.
кГ
дин
Н
1
9810
9
,
81
1 1
Поверхностное
натяжение
уменьшается
с
повышением
радиусы
кривизны
м
см
м r1 и r2 -pглавные
где
температуры. Силы поверхностного
натяжения
учитывать
r1 нужно
rжидкости.
поверхности
элемента
2
при движении жидкости в капиллярах, при барботаже газа и т.п.
9. Вязкость
Вязкость является результатом действия трения междусоприкасающимися слоями жидкости, вследствие чего
эти слои движутся с различными скоростями.
Для расчета силы трения обычно используют закон Ньютона.
Этот закон обобщенно характеризует механические
свойства сплошных сред и распространяется на воду,
воздух, спирты и многие другие жидкости и газы.
Ньютоновскими называются жидкости, удовлетворяющие
обобщенному закону Ньютона в форме:
Tтр
w
F
n
10. Вязкость
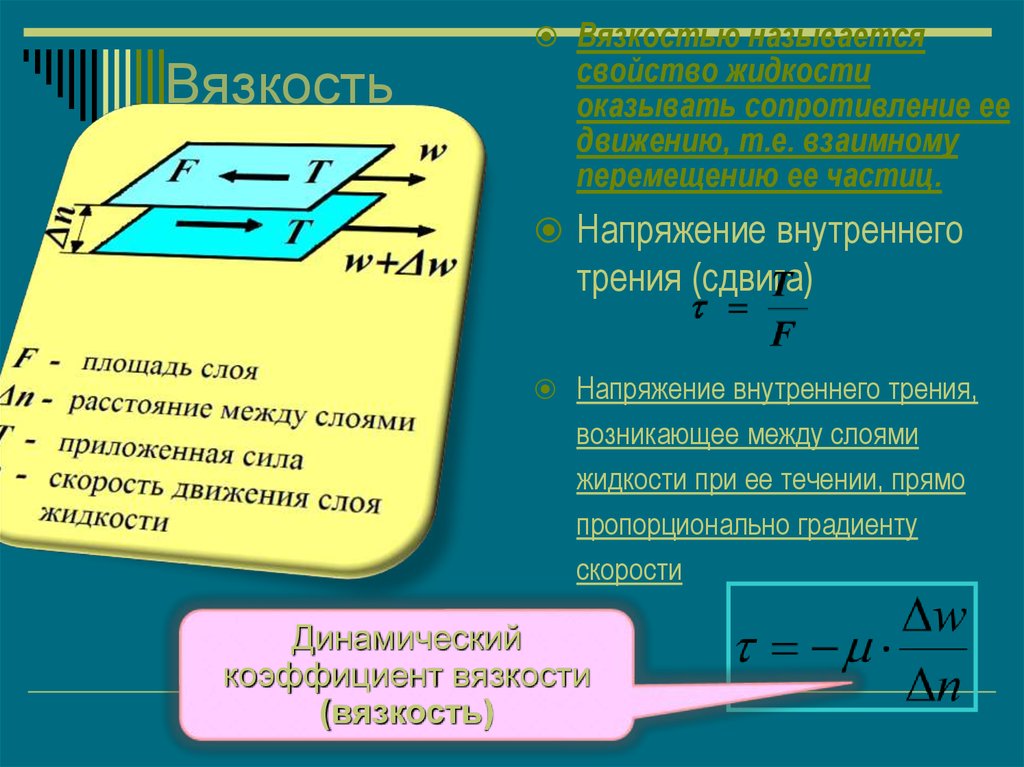
Вязкостью называетсясвойство жидкости
оказывать сопротивление ее
движению, т.е. взаимному
перемещению ее частиц.
Напряжение внутреннего
трения (сдвига)
Напряжение внутреннего трения,
возникающее между слоями
жидкости при ее течении, прямо
пропорционально градиенту
скорости
Динамический
коэффициент вязкости
(вязкость)
11.
Единицы измерения вязкости μ:Соотношение между Па*с и П:
Кинематический коэффициент вязкости или кинематическая вязкость ν:
Единицы измерения кинематической вязкости :
12. ГИДРОСТАТИКА
Гидростатическое давлениеАтмосферное давление
Дифференциальные уравнения равновесия Эйлера
Равновесие тела в покоящейся жидкости
Давление на плоскую стенку
Давление на криволинейную стенку
Практические задачи
13. Не для конспекта
Ответ. Злобный джинн, находящийся вгазообразном
состоянии
внутривбутылки, весь
Злобный
джинн,
находящийся
газообразном
состоянии
внутри
состоит из
маленьких
злобных молекул,
закупоренной
сильное
которые, как ибутылки,
молекулыоказывает
любого другого
газа,
давление
ее стенки,
дно и пробку.
ЧемИми
все на
время
беспорядочно
движутся.
давит джинн, если
в газообразном
джинн
и лупит во все стороны!
состоянии не имеет ни рук, ни ног, ниГ.Остер
других
частей тела?
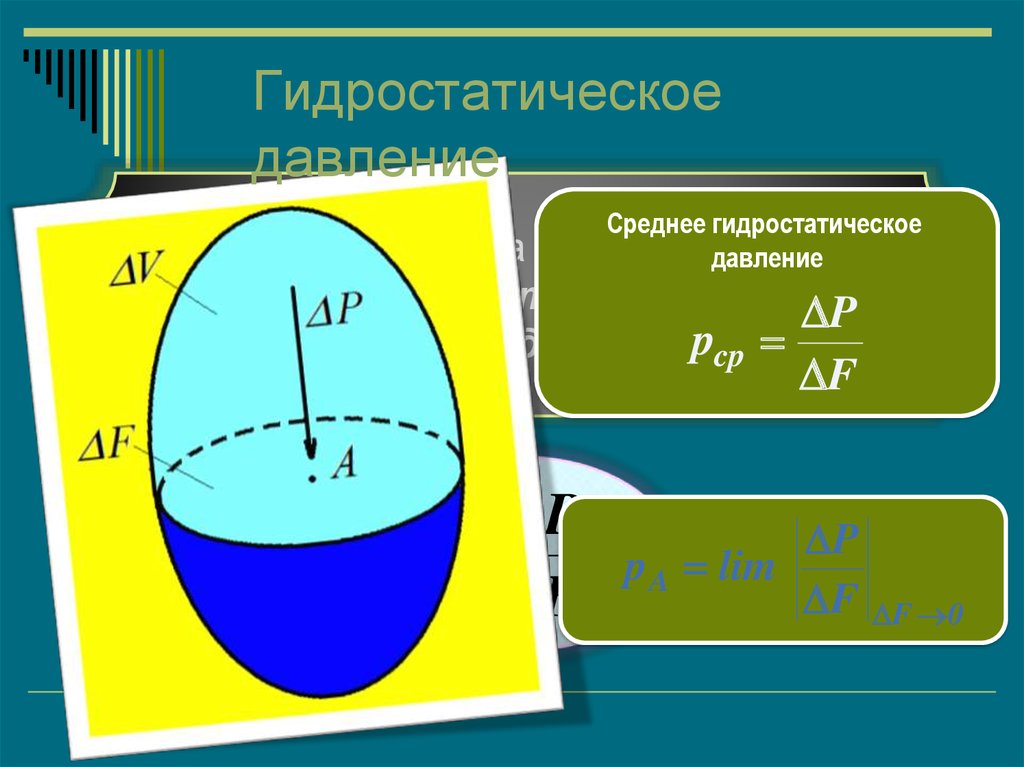
14. Гидростатическое давление
Среднее гидростатическоеединицу поверхности
давление
Давление жидкости на
называется гидростатическим давлением
P
pcp
или просто давлением.
F
P
p
F
P
p A lim
F
F 0
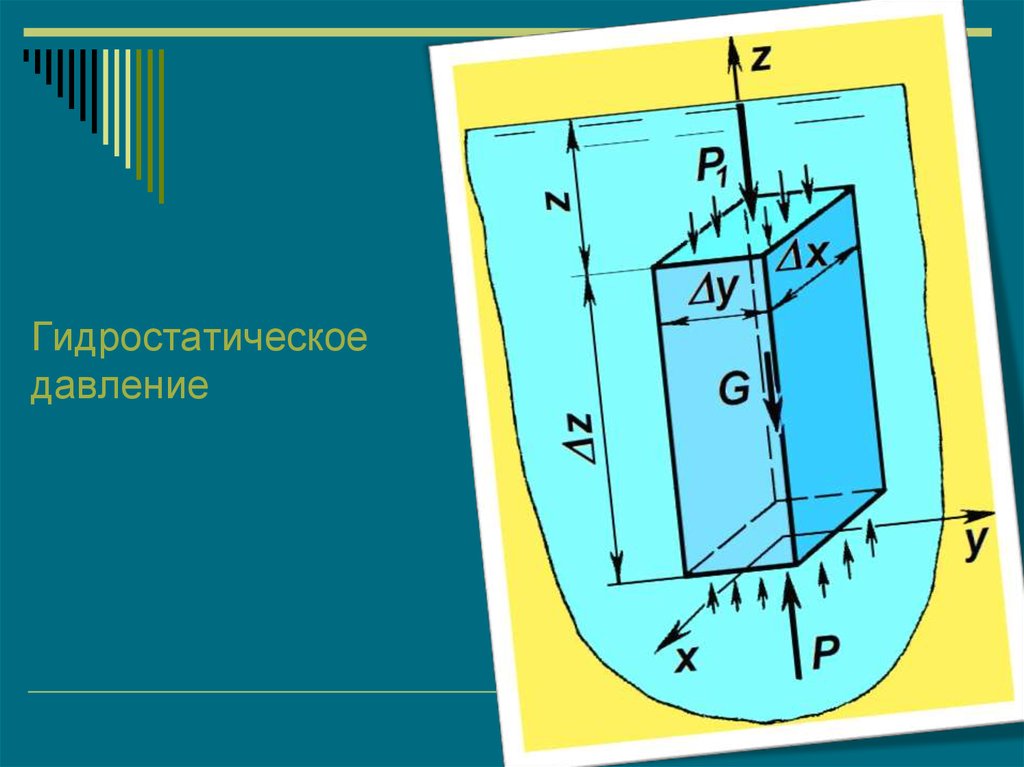
15. Гидростатическое давление
16.
Гидростатическое давлениеОчевидно, равнодействующая всех
сил, направленных вертикально,
будет равна нулю, так как тело
находится в равновесии.
P P1 G 0
p x y p1 x y g z x y 0
p p1 g z
Гидростатическое давление в жидкости
пропорционально высоте
ее слоя уравнение
основное
и на одинаковой глубине
имеет одну и ту же величину во всехгидростатики
точках жидкости.
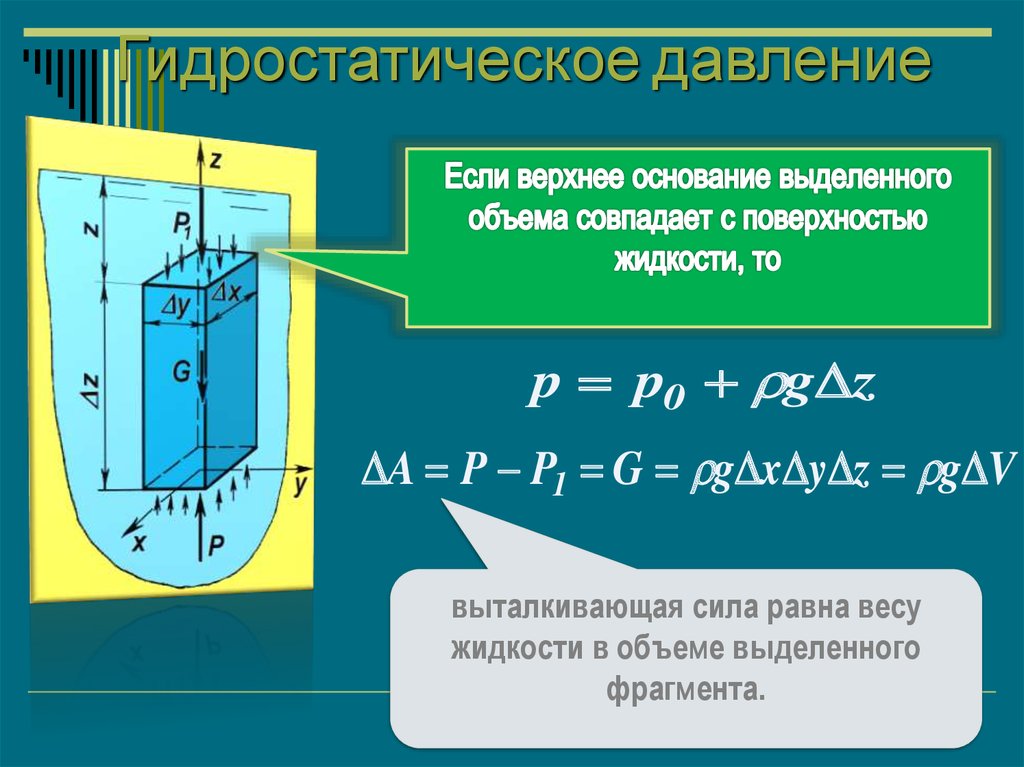
17.
Гидростатическое давлениеp p0 g z
A P P1 G g x y z g V
выталкивающая сила равна весу
жидкости в объеме выделенного
фрагмента.
18. Гидростатическое давление
В замкнутом сосуде давление, производимоеГидростатическое
давление
направлено
по
внешними силами
на жидкость
или газ,
нормали
к поверхности,
которую
оно
передается
без
изменения пона
всем
направлениям
действует,
величина
его в данной
точке
в каждуюаточку
жидкости
или газа.
не зависит от направления.
(закон Паскаля)
Если бы гидростатическое давление было направлено
Почему
еще никому не
удалось бы силы,
не по нормали
к поверхности,
то появились
надутьвдоль
квадратный
воздушный
действующие
поверхности,
что вызвало бы
шарик,
чтобы онОднако,
летал вэто
виде
перемещение
жидкости.
противоречит
куба? находится в покое.
условию, что жидкость
Вторая часть условия вытекает из основного
уравнения гидростатики: величина давления зависит
только от плотности жидкости и глубины погружения.
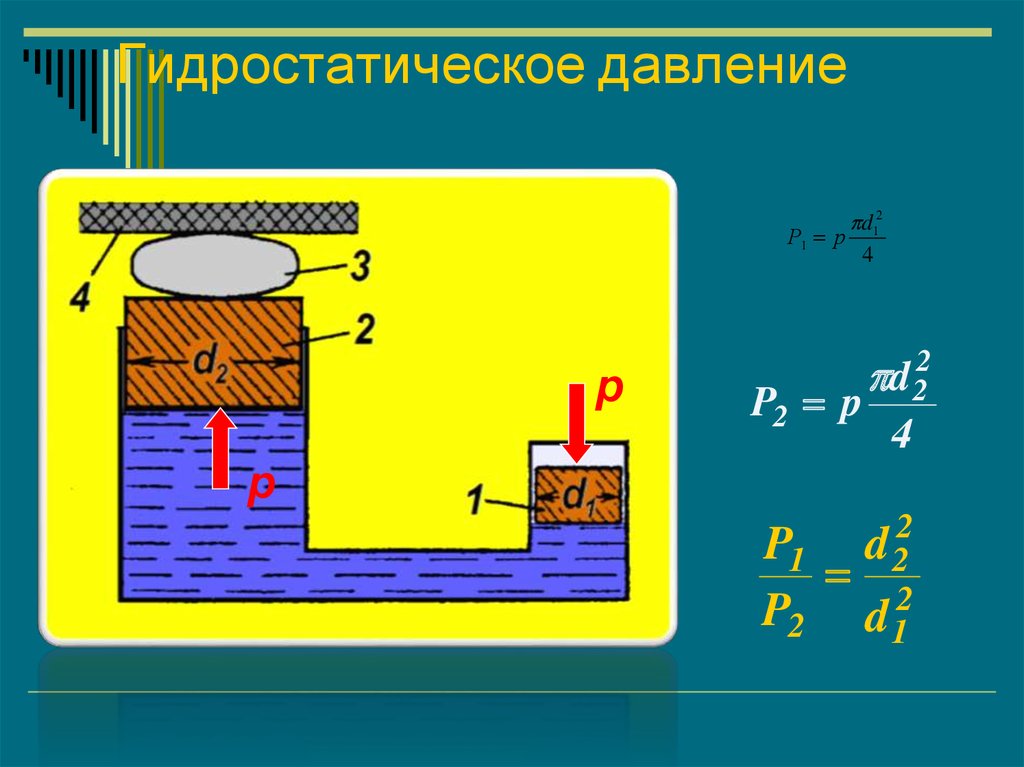
19. Гидростатическое давление
Р1 рр
d12
4
P2 p
р
P1
P2
d 22
4
2
d2
d 12
20. Атмосферное давление
Атмосферное давление - это сила,действуюшая со стороны воздушной атмосферы
на единицу площади поверхности Земли
в перпендикулярном к поверхности направлении.
Среднюю величину атмосферного давления
можно получить, если разделить вес всех молекул
воздуха на площадь поверхности Земли.
вес молекул воздуха
pатм площадь поверхности Земли
ратм
Н
101325 Па 101325 2 760 мм рт .ст .
м
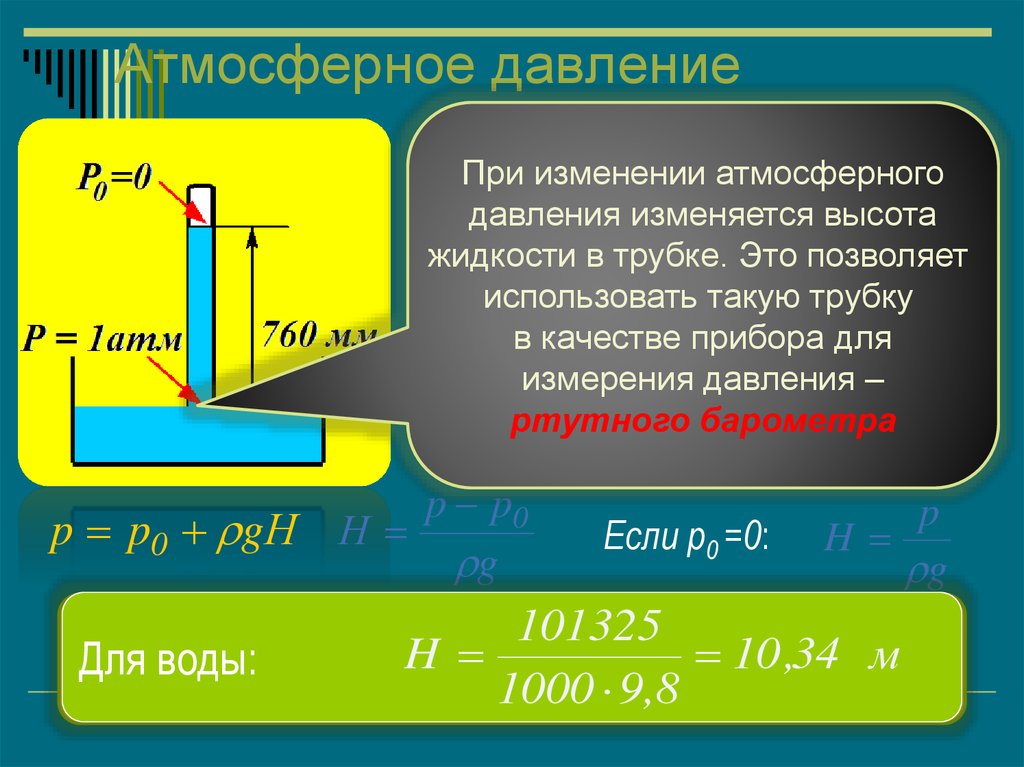
21. Атмосферное давление
ПриЕслиизменении
атмосферного
в жидкую ртуть опустить трубку,
давления
изменяется
высота
в которой создан
вакуум, то ртуть
под
действием
давленияЭто
поднимается
жидкости
в трубке.
позволяет
в ней на такую высоту, при которой
использовать
такую трубку
давление столба жидкости станет
в равным
качестве
прибора
для
внешнему
атмосферному
давлению на открытую
поверхность
измерения
давления
–
ртутногортути
барометра
p p0
p p0 gН Н
g
воды:
Для ртути:
Если р0 =0:
p
H
g
101325
101325
H
H
010
,76,34мм
1000 99,8
13600
,8
22. Атмосферное давление
Можно ли, пользуясьпоршневым насосом, через
шланг накачать воду из лужи во
дворе в большую химическую
аудиторию, которая находится
на третьем этаже института на
высоте примерно 15 м?
23. Атмосферное давление
давлениеpАтмосферное
gН
атм p
вх не только
должно поднять воду к насосу
на
но и создать
А высоту
сюдаH,носите
движение
жидкости и преодолеть
101325
воду
ведрами!
H силу
10 ,34
трения.
На практике
1000всасывания
9,8 насоса
высота
не превышает 5-6м
Торичелли: не насос втягивает воду, а атмосферное
давление её поднимает вверх, когда на всасывающей линии
насоса образуется разреженное пространство (рвх < ратм)
м
24. Давление абсолютное, избыточное и разрежение (вакуум).
p Н gНСоотношения
между единицамидавление:
измерения давления:
Абсолютное
1 атм (физ)= 760 мм рт.ст.=10,33 м вод.ст. =
= 1,033 кгс/см2
кгс/м2 = 101300
абс =10330ман
атмн/м2 (Па)
1 ат (техн) = 735,6 мм рт.ст. =10 м вод.ст. =1 кгс/см2 =
[ата]
[ати]
[атм]
=10000 кгс/м2
= 98100 н/м2.
р
р
р
Вакуум (разрежение)
Приборы для измерения давления (манометры, вакуумметры)
показывают не абсолютное давление внутри замкнутого объема, а
разность между абсолютным и атмосферным, или барометрическим,
давлением. Эту разность называют избыточным давлением [ати].
рвак ратм рабс
25.
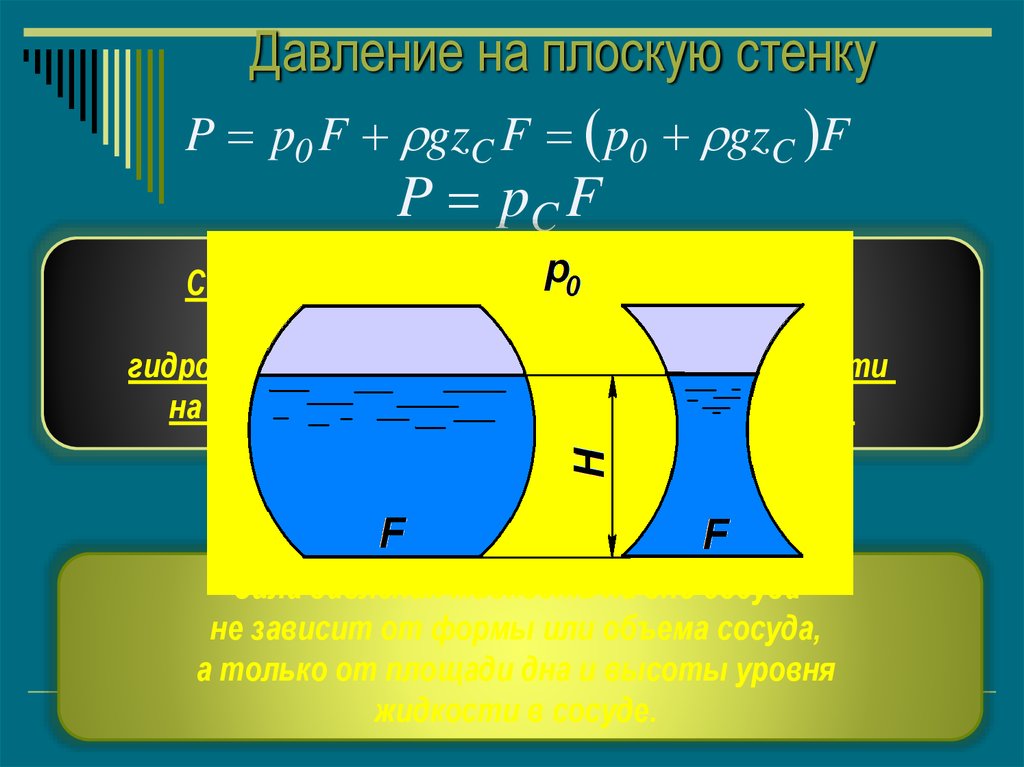
Давление на плоскую стенкуP p0 F gzC F p0 gzC F
P pC F
Сила давления жидкости на плоскую стенку
равна произведению величины
гидростатического давления в ее центре тяжести
на величину площади смоченной поверхности.
P p0 gH F
Cила давления жидкости на дно сосуда
не зависит от формы или объема сосуда,
а только от площади дна и высоты уровня
жидкости в сосуде.
26. ГИДРОДИНАМИКА
Основные характеристики движения жидкостейСкорость и расход жидкости
Уравнение неразрывности потока
(Материальный баланс потока)
Уравнение Бернулли (Энергетический баланс потока)
Режимы движения жидкости
Распределение скоростей по сечению потока при ламинарном и турбулентном
режимах
Элементы теории подобия
Некоторые практические приложения уравнения Бернулли
Движение жидкости в напорных трубопроводах и их расчет
Практические задачи
27.
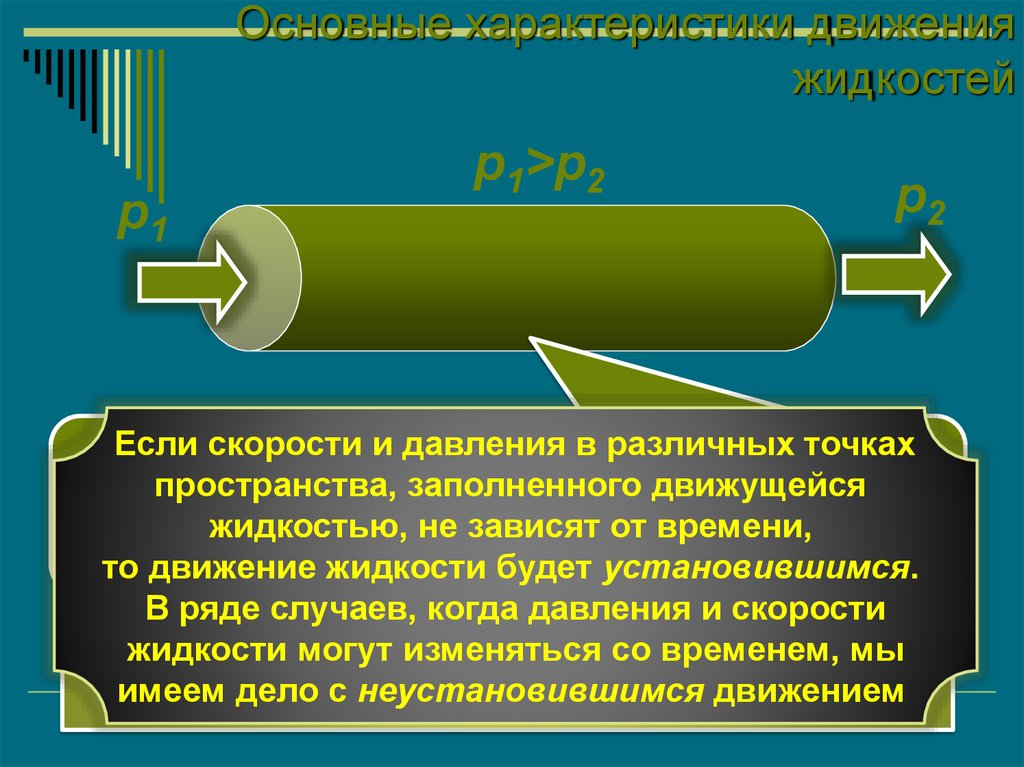
Основные характеристики движенияжидкостей
p1
p1>p2
p2
Если скорости
давления
различных
точках
Движущей
силойипри
течениивжидкостей
является
пространства, заполненного движущейся
разность давлений, которая создается с
жидкостью, не зависят от времени,
помощью насосов или компрессоров…
то движение жидкости будет установившимся.
В ряде случаев, когда давления и скорости
жидкости
изменяться
со временем,
…либомогут
вследствие
разностей
уровней мы
имеем дело
с неустановившимся
или
плотностей жидкости движением
28. Основные характеристики движения жидкостей
ЧастицаA
E
B
C
D
Скорости всех частиц жидкости,
находящихся в данный момент на
рассматриваемой линии тока,
касательны к ней.
Траектория
движения
частицы
Совокупность частиц
A,B,C,D,E и др., находящихся
в данный момент на одной
траектории, образует линию
тока.
При установившемся движении траектория отдельной
частицы и линия тока будут совпадать.
29.
Основные характеристики движенияжидкостей
Трубка тока - совокупность линий тока, проведенных
через площадку ΔF.
При ΔF → 0 трубка тока вырождается в линию тока.
При установившемся движении трубки тока остаются
неизменными.
30.
Основные характеристики движенияжидкостей
Поток жидкости – совокупность элементарных струек,
движущихся с разными скоростями
Живое сечение потока сечение потока, проведенное перпендикулярно
к направлению линий тока.
Напорное движение
Безнапорное движение
Смоченный периметр - часть периметра канала,
соприкасающаяся с движущимся потоком.
31.
Основные характеристики движенияжидкостей
Гидравлический (эквивалентный) радиус отношение площади живого сечения потока F к
смоченному периметру П
Гидравлический (эквивалентный) диаметр:
Для круглой трубы при сплошном заполнении ее
Понятия гидравлических радиуса и диаметра
жидкостью
позволяют использовать уравнения гидравлики
для трубопроводов (каналов), имеющих
некруглую форму поперечного сечения
32. Скорость и расход жидкости
Расход - количество жидкости, протекающее черезживое сечение потока в единицу времени.
Массовый m и объемный Q расходы связаны
соотношением
Если расход жидкости через поперечное сечение ΔFi
элементарной струйки составляет ΔQ, то средняя
скорость жидкости в данном сечении wi равна
Общий расход потока
Средняя скорость потока
Массовая скорость потока
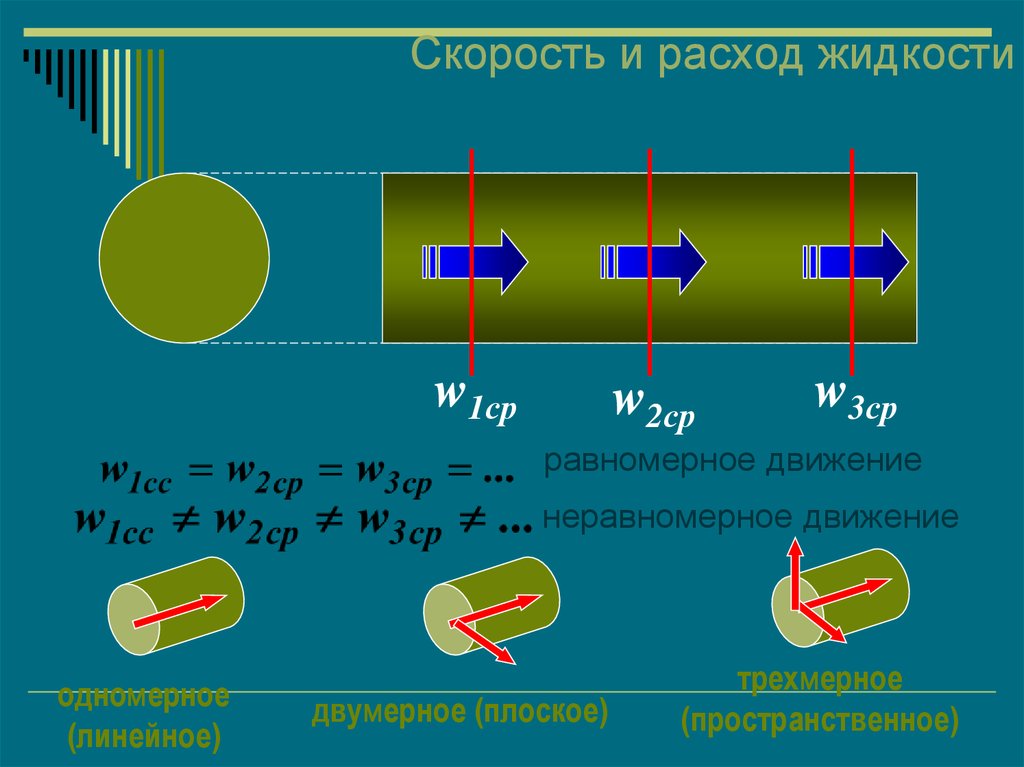
33. Скорость и расход жидкости
w1срw2ср
w3ср
равномерное движение
неравномерное движение
одномерное
(линейное)
двумерное (плоское)
трехмерное
(пространственное)
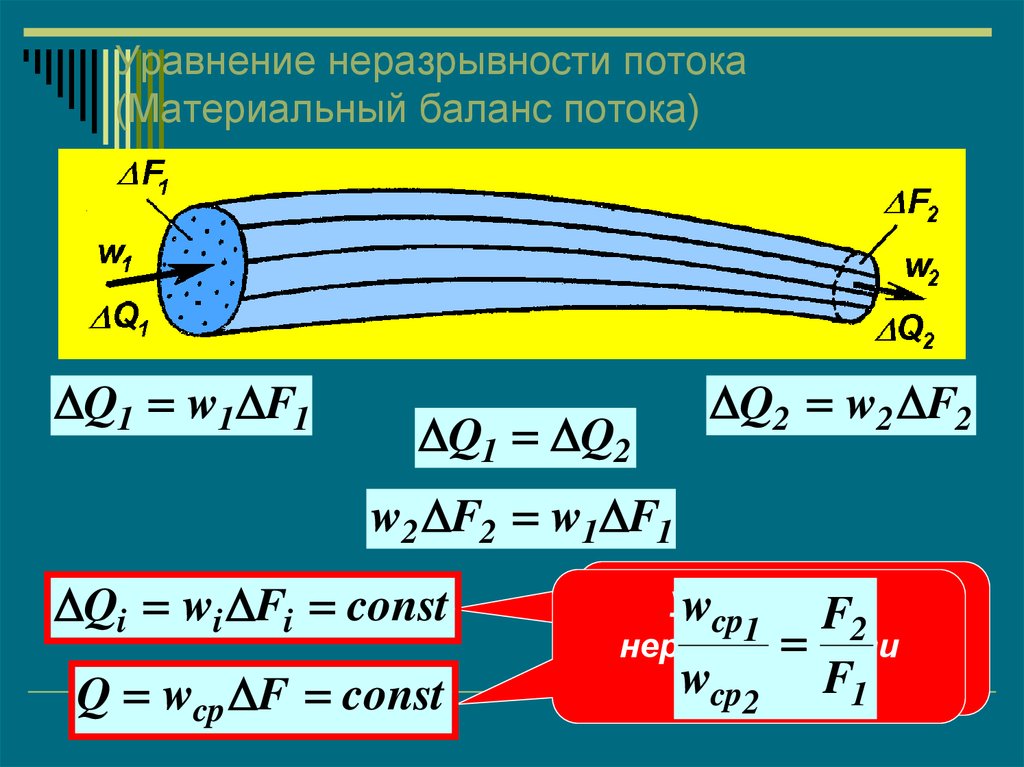
34. Уравнение неразрывности потока (Материальный баланс потока)
Q1 w1 F1Q1 Q2
Q2 w2 F2
w2 F2 w1 F1
Qi wi Fi const
Q wcp F const
Уравнение
wУравнение
F2
cp1
неразрывности
неразрывности
wпотока
F
cpструи
1
2
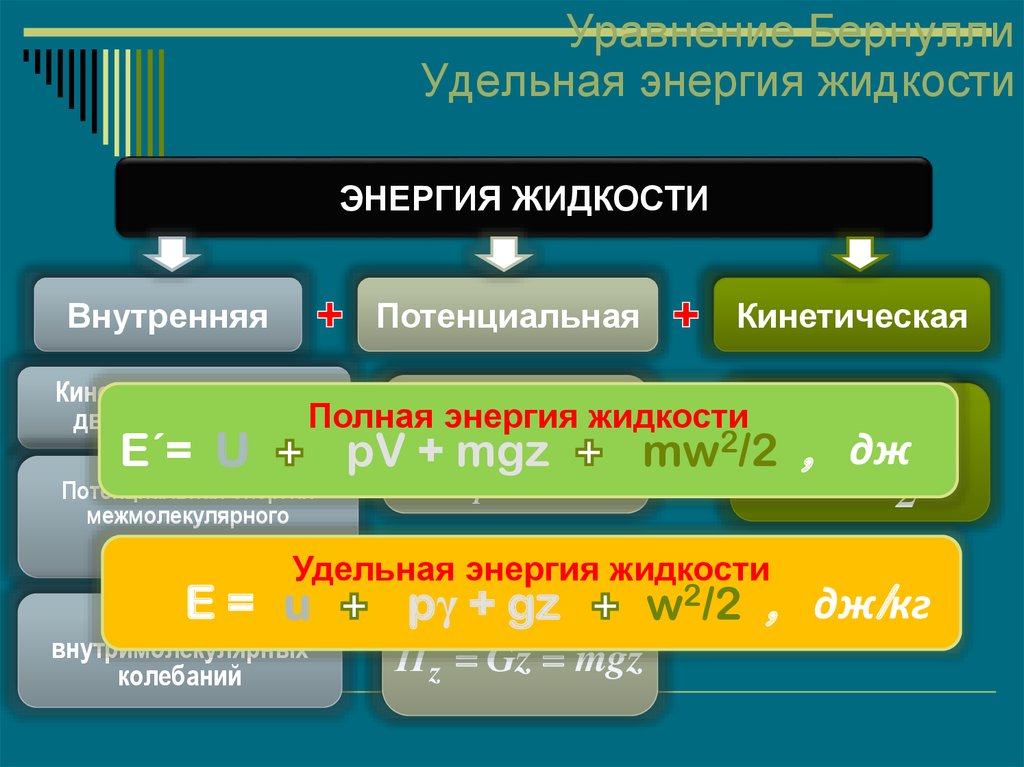
35. Уравнение Бернулли Удельная энергия жидкости
ЭНЕРГИЯ ЖИДКОСТИВнутренняя
Потенциальная
Кинетическая
Кинетическая энергия
Энергия
движения молекул Полная энергия жидкости
E´= U
Потенциальная энергия
межмолекулярного
притяжения
pV +Пдавления
mgz
pV
р
2
mw
mw2/2K, дж
2
Удельная Энергия
энергия жидкости
pγположения
+ gz
u
w2/2 ,
E=
Энергия
внутримолекулярных
колебаний
П z Gz mgz
дж/кг
36. Уравнение Бернулли для идеальной жидкости
w12w22
u1 p1 gz1
u2 p2 gz2
2
2
w12
p2
w22
u1
gz1
u2
gz2
2
2
p1
u1=u2
Уравнение Бернулли является
частным случаем
p1 закона
w12 сохранения
p2 энергии
w22
z1 энергетический
z2
потока:
и выражает
баланс
g 2 g
g 2 g
полная удельная энергия жидкости
есть величина постоянная
во
всех сечениях
потока.
уравнение
Бернулли
для идеальной жидкости.
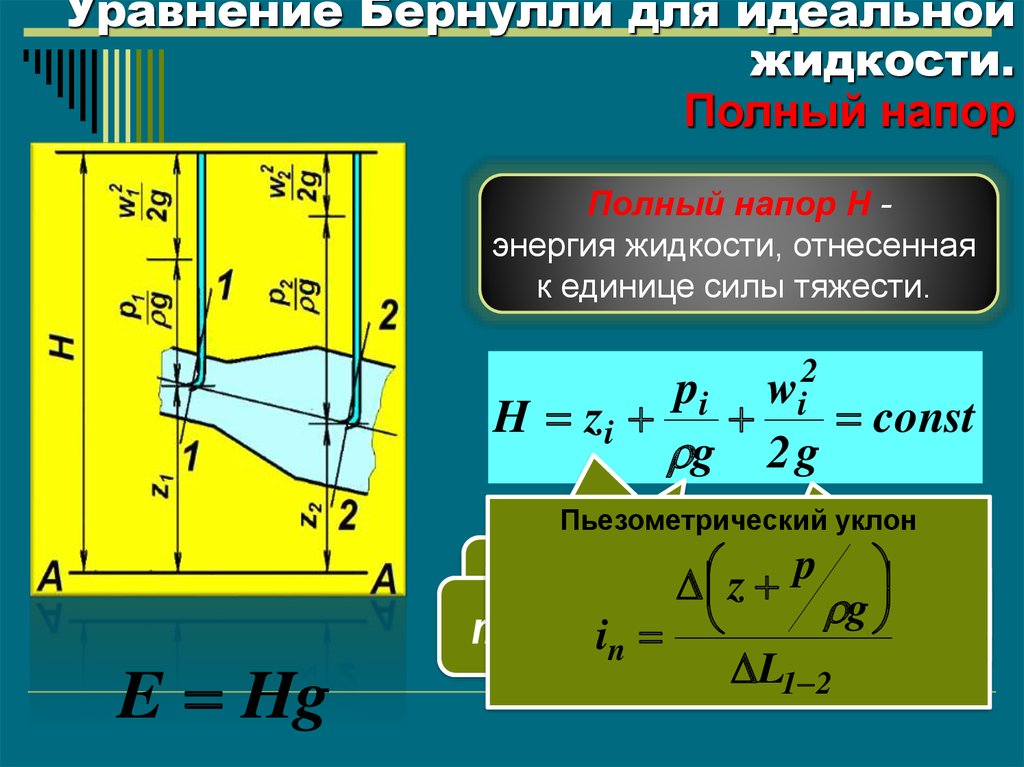
37.
Уравнение Бернулли для идеальнойжидкости.
Полный напор
Полный напор Н энергия жидкости, отнесенная
к единице силы тяжести.
pi wi2
H zi
const
g 2 g
Пьезометрический уклон
E Hg
p
z
геометрический
напор
скоростной
напор
g
пьезометрический
напор
in
L1 2
38. Уравнение Бернулли для реальной жидкости
w12p2
w22
u1
gz1
u2
gz2
2
2
p1
w12
p2 w22
gz1 от идеальной
gz2 жидкости,
u2 которой
u1
В отличие
для
2
2
p1
полный напор Н = const,
для реальной
p1 w12жидкостиp2полный
w22 напор
z1 по
направлению
z2 движения
жидкости.
h1 2
убывает
g
2g
g
2g
Из уравнения Бернулли следует, что
увеличение
скоростного
напора
уравнение
Бернулли
сопровождается
соответствующим
уменьшением
для реальной
жидкости.
пьезометрического напора и наоборот.
39.
Уравнение Бернулли для реальнойжидкости.
Полный напор
H 1 H 2 h1 2
h1 2
u2 u1
g
Гидравлический
уклон:
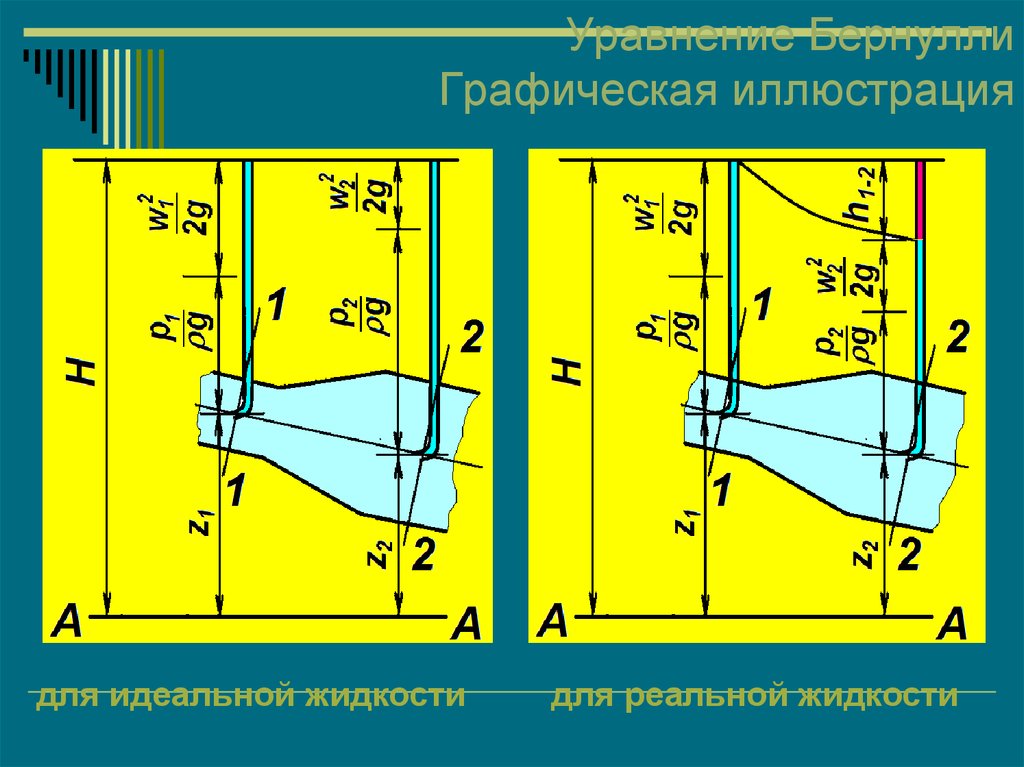
40. Уравнение Бернулли Графическая иллюстрация
для идеальной жидкостидля реальной жидкости
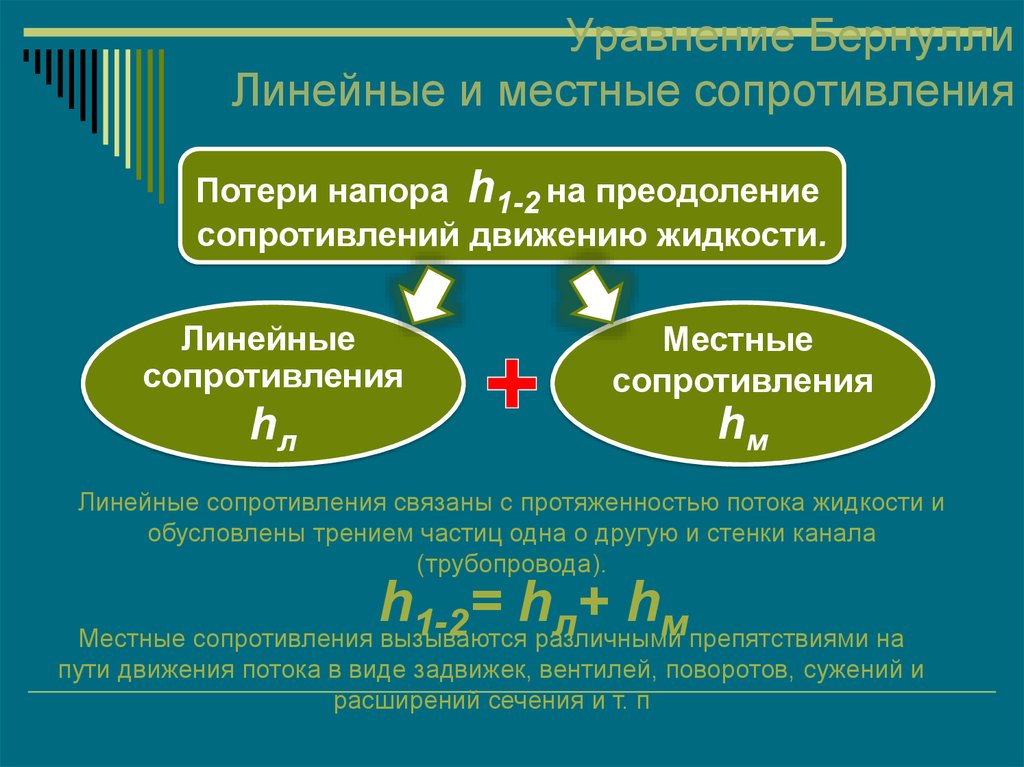
41. Уравнение Бернулли Линейные и местные сопротивления
Потери напора h1-2 на преодолениесопротивлений движению жидкости.
Линейные
сопротивления
Местные
сопротивления
hл
hм
Линейные сопротивления связаны с протяженностью потока жидкости и
обусловлены трением частиц одна о другую и стенки канала
(трубопровода).
h
=
h
+
h
1-2
л
мпрепятствиями на
Местные сопротивления вызываются различными
пути движения потока в виде задвижек, вентилей, поворотов, сужений и
расширений сечения и т. п
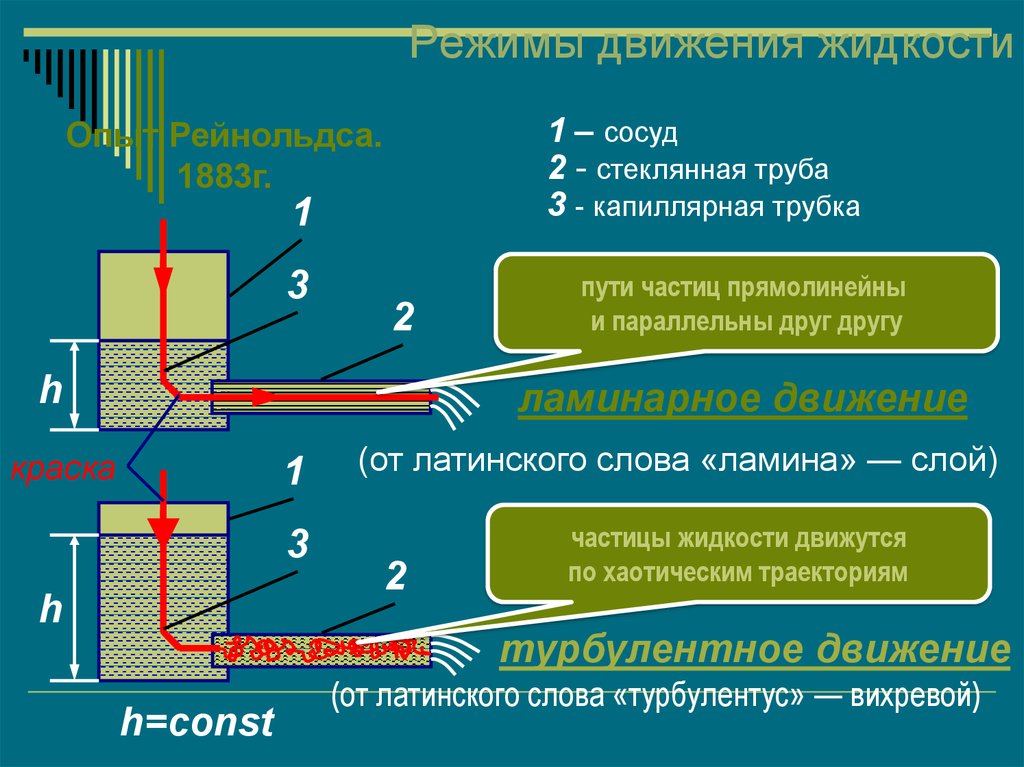
42. Режимы движения жидкости
1 – сосуд2 - стеклянная труба
3 - капиллярная трубка
Опыт Рейнольдса.
1883г.
1
3
2
h
пути частиц прямолинейны
и параллельны друг другу
ламинарное движение
краска
1
3
h
(от латинского слова «ламина» — слой)
2
частицы жидкости движутся
по хаотическим траекториям
турбулентное движение
h=const
(от латинского слова «турбулентус» — вихревой)
43.
Режимы движения жидкостиОпыт показывает, что переход от ламинарного
течения к турбулентному зависит от массовой
скорости жидкости ρw, диаметра трубы d
и вязкости жидкости μ.
Критерий Рейнольдса:
Reкр=2300
Re
wd
wd
Re < 2300 – устойчивый ламинарный режим
2300 < Re < 10000 – неустойчиво турбулентный режим
Re > 10000 – устойчиво турбулентный режим
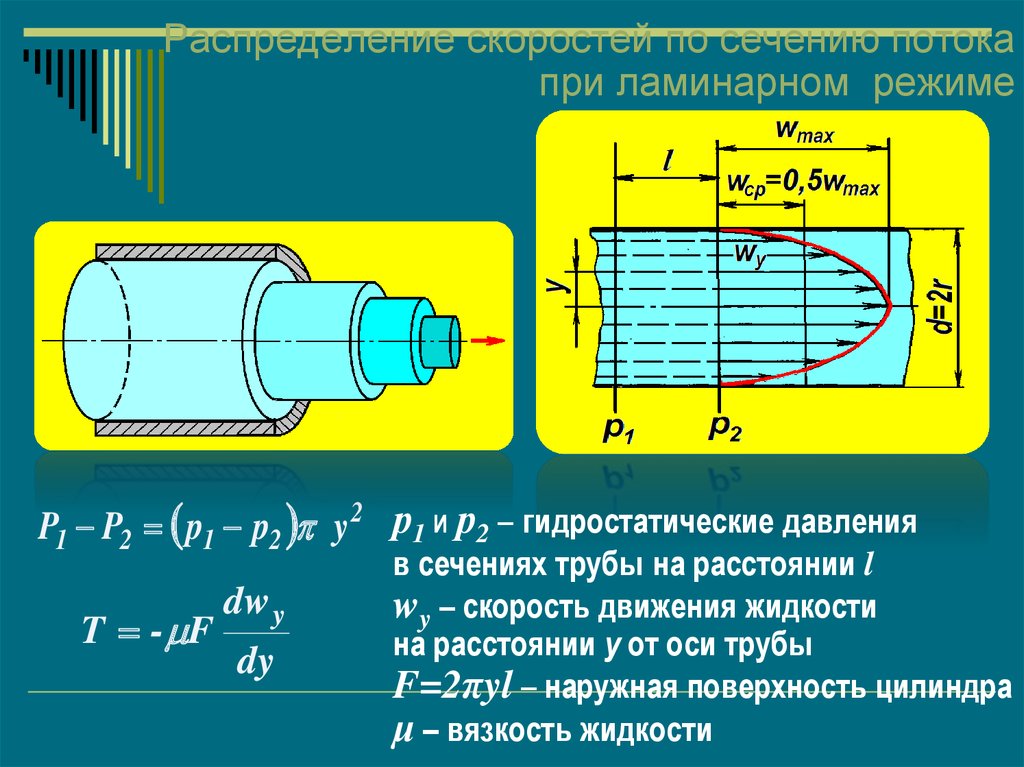
44. Распределение скоростей по сечению потока при ламинарном режиме
P1 P2 p1 p2 y 2 р1 и р2 – гидростатические давленияT - F
dw y
dy
в сечениях трубы на расстоянии l
wy – скорость движения жидкости
на расстоянии y от оси трубы
F=2πyl – наружная поверхность цилиндра
μ – вязкость жидкости
45.
Распределение скоростей по сечению потокапри ламинарном режиме
Сумма проекций всех сил на ось потока равна нулю
p1 p2 y
2
2 yl
dw y
dy
После сокращения и разделения переменных
p1 p2
ydy dw y
2 l
Проинтегрируем по всему объему жидкости в трубе
0
p1 p2
ydy dw y
y 2 l
wy
r
Получаем
p1 p2 2
p1 p2 r 2 y 2
wy
wy
r y2
4 l
или
2 l 2
2
46.
Распределение скоростей по сечению потокапри ламинарном режиме
Скорость имеет максимальное значение на оси трубы
wmax
p1 p2 2
r
4 l
y2
w y wmax 1 2
r
- закон Стокса, выражающий параболическое
распределение скоростей в сечении трубопровода
при ламинарном движении
При ламинарном потоке средняя скорость жидкости
равна половине скорости по оси трубы
wcp 0 ,5 wmax
47.
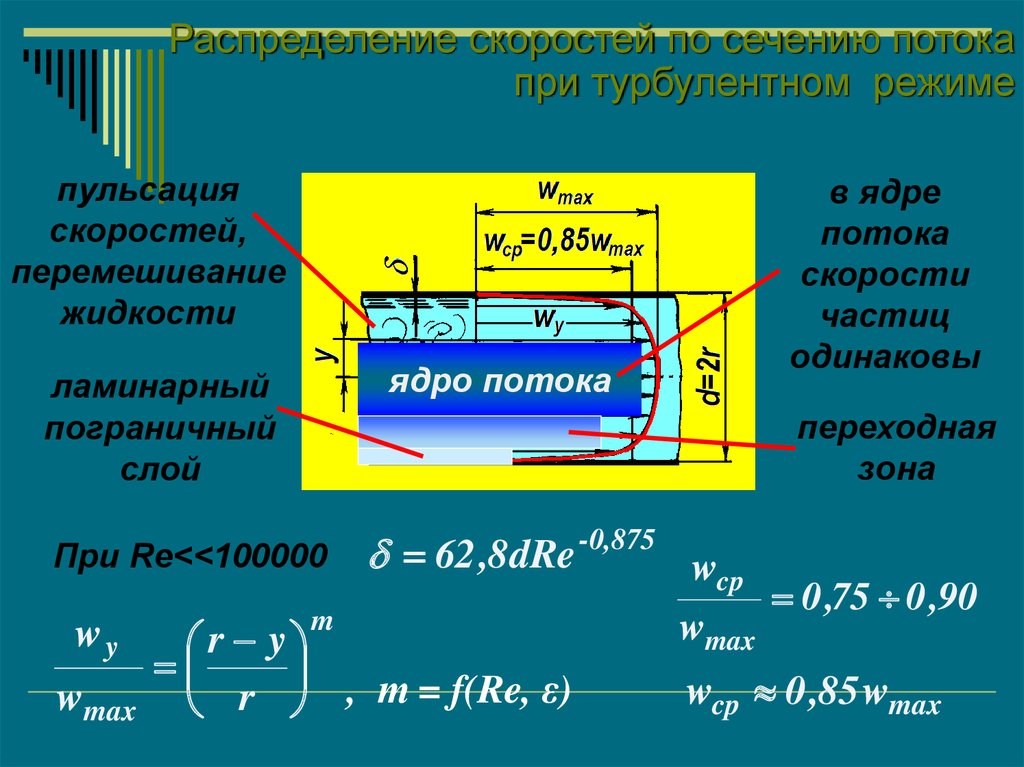
Распределение скоростей по сечению потокапри турбулентном режиме
пульсация
скоростей,
перемешивание
жидкости
ядро потока
ламинарный
пограничный
слой
переходная
зона
При Re<<100000
wy
wmax
r
r
в ядре
потока
скорости
частиц
одинаковы
m
62 ,8 dRe -0,875 w
cp
y
, т = f(Re, ε)
wmax
0 ,75 0 ,90
wcp 0 ,85 wmax
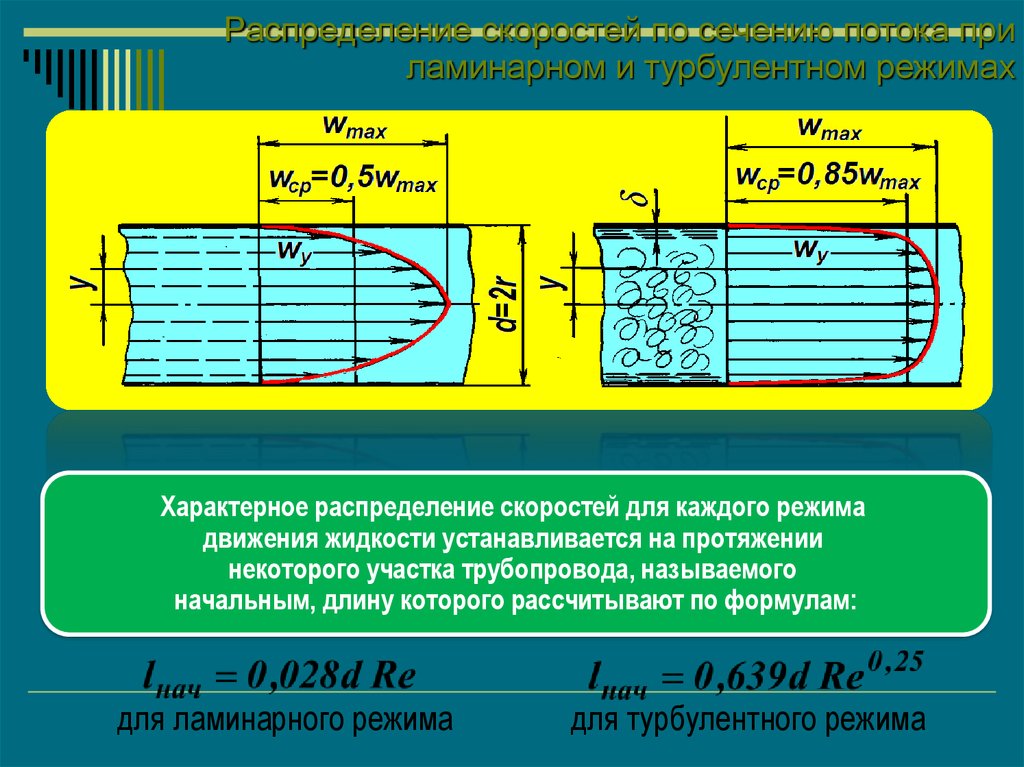
48.
Распределение скоростей по сечению потока приламинарном и турбулентном режимах
Характерное распределение скоростей для каждого режима
движения жидкости устанавливается на протяжении
некоторого участка трубопровода, называемого
начальным, длину которого рассчитывают по формулам:
для ламинарного режима
для турбулентного режима
49. Некоторые практические приложения уравнения Бернулли
Расчет сопротивлений и потерь напорапри движении жидкости по трубопроводу
Измерение скоростей и расходов
жидкости
50. Сопротивление при движении жидкости по трубопроводу
При движении реальной жидкости по трубопроводу иликаналу
происходит
потеря
напора
,
которая
складывается из:
потери на трение частиц жидкости друг о друга и о
стенки трубы или канала,
потери
на
местных
сопротивлениях,
которые
изменяют направление или скорость потока.
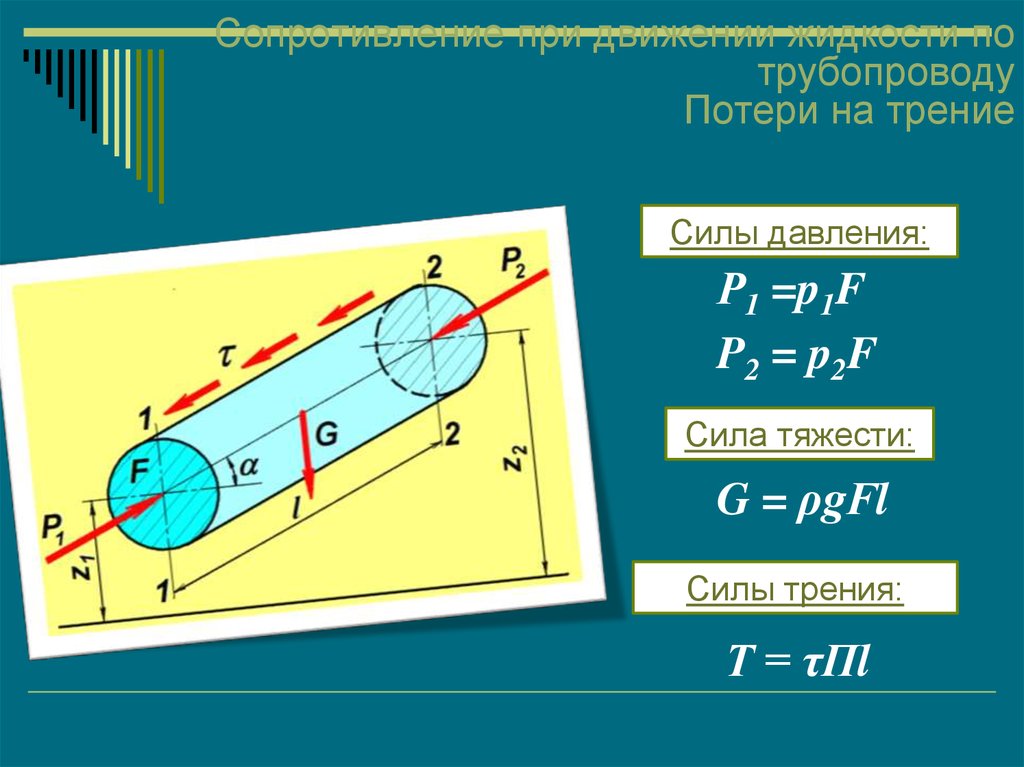
51. Сопротивление при движении жидкости по трубопроводу Потери на трение
Силы давления:Р1 =p1F
P2 = p2F
Сила тяжести:
G = ρgFl
Силы трения:
Т = τПl
52.
Сопротивление при движении жидкости потрубопроводу
Потери на трение
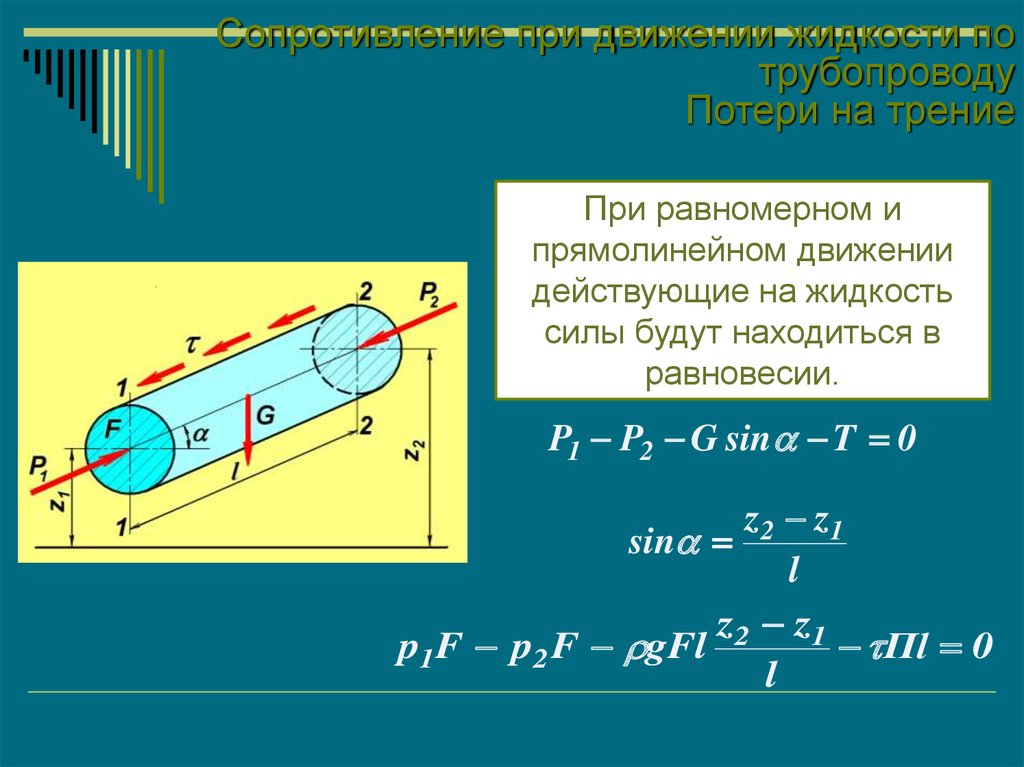
При равномерном и
прямолинейном движении
действующие на жидкость
силы будут находиться в
равновесии.
P1 P2 G sin T 0
z 2 z1
sin
l
z 2 z1
p1F p2 F gFl
Пl 0
l
53.
Сопротивление при движении жидкости потрубопроводу
Потери на трение
Разделим уравнение на ρgF :
p1
p2 Пl
l
z1 z 2
g
g gF g rгидр
l
4
l
Потери напора при
h1- 2
g rгидр g d гидр
равномерном движении:
Потеря напора на трение может
быть выражена через скоростной
напор w2/2g:
h1- 2
w2
2g
где ζ — коэффициент потерь энергии по длине или
коэффициент сопротивления трения.
54.
Сопротивление при движении жидкости потрубопроводу
Потери на трение
Напряжение трения τ:
Введем обозначение:
— коэффициент гидравлического сопротивления
(коэффициент трения)
55.
Сопротивление при движении жидкости потрубопроводу
Потери на трение
Потери напора на трение:
h1 2
w2
d гидр 2 g
l
Для
трубопровода
Потеря напора
накруглого
трение пропорциональна
длине
dгидр =напору
d
трубопровода l и скоростному
w2/2g и обратно
пропорциональна диаметру трубы d.
64
k
быть
f Re,
При
турбулентном
режиме:
Для
гладких труб и при
Re<70000 может
Re
0 ,3165
использована формула Блазиуса:
d
Для ламинарного режима:
ε - относительная шероховатость стенок трубы;0,25
Re
k – абсолютная шероховатость (средняя величина выступов на
стенках трубопровода);
56.
Сопротивление при движении жидкостипо трубопроводу
Местные сопротивления
К местным сопротивлениям относятся вход в трубу
и выход из нее, участки сжатия и расширения потока,
различные фитинги, диафрагмы, запорные и
регулирующие устройства.
Потери напора в местном
сопротивлении:
где ξм — коэффициент местного сопротивления.
Величина ξм зависит как от вида местного
сопротивления, так и от режима движения жидкости,
т.e. от числа Рейнольдса. Для различных местных
сопротивлений величины ξм приводятся
в справочниках.
57.
Сопротивление при движении жидкости потрубопроводу
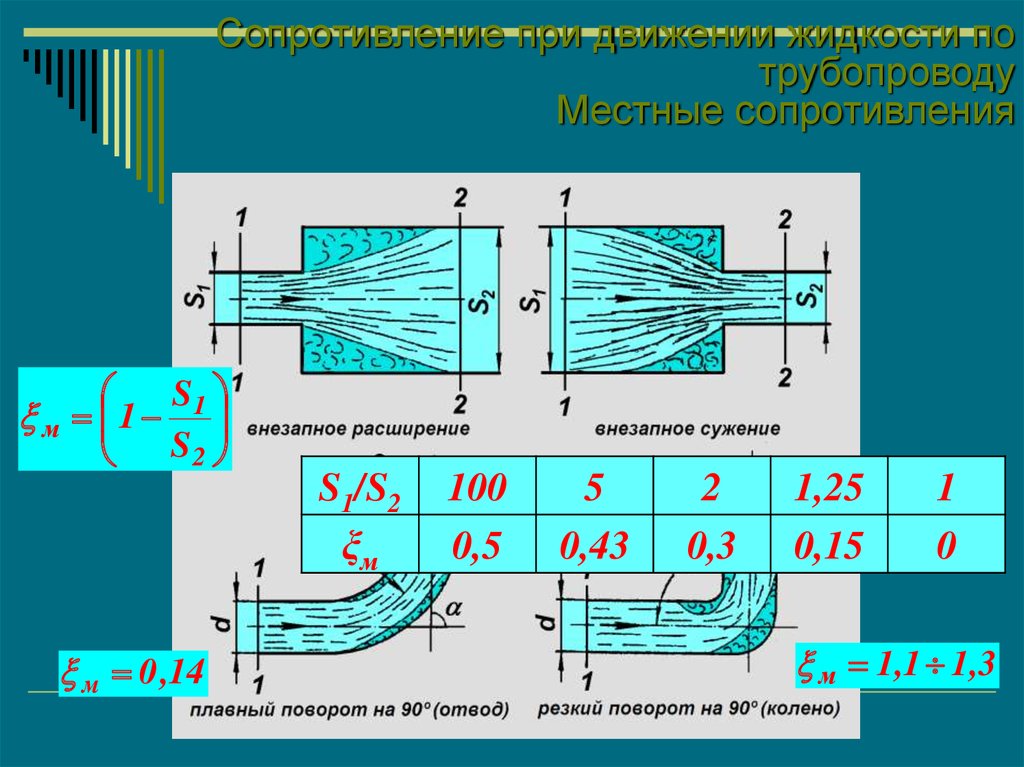
Местные сопротивления
S1
м 1
S2
S1/S2
ξм
м 0 ,14
100
0,5
5
0,43
2
0,3
1,25
0,15
1
0
м 1,1 1,3
58.
Сопротивление при движении жидкости потрубопроводу
Общая потеря напора
Полную потерю напора определяют как сумму всех
потерь:
2
l w2
w2 l
w
h hл hм
м ,i
м ,i
d 2g
2g d
2g
При движении жидкости по горизонтальному
трубопроводу (z1=z2) с постоянной скоростью
(w1=w2) полная потеря напора составит:
p1 p2
h
g
Потеря давления
в трубопроводе:
Потери давления
в трубопроводе
только от трения:
2
2
l
w
w
Н Н
p h
g p
,2
i ,
2
d
2
2
м
м
59. Использованная литература
Арустамова И.Т., Иванников В.Г. Гидравлика: Учебное пособие дляВУЗов (Рекомендовано ГК РФ по высшему образованию) – М.: Недра.
1995 -198 стр.
Кононов А.А., Кобзов Д.Ю., Кулаков Ю.Н., Ермашонок С.М. Основы
гидравлики: Курс лекций. - Братск: ГОУ ВПО "БрГТУ", 2004 . - 102 с.



































 Физика
Физика








