Кинематическое исследование механизмов и машин

1.

ТЕОРИЯ МЕХАНИЗМОВ И МАШИН
1

2.

Кинематика зубчатых передач
2

3.

Кинематический анализ зубчатых механизмов
3

4.

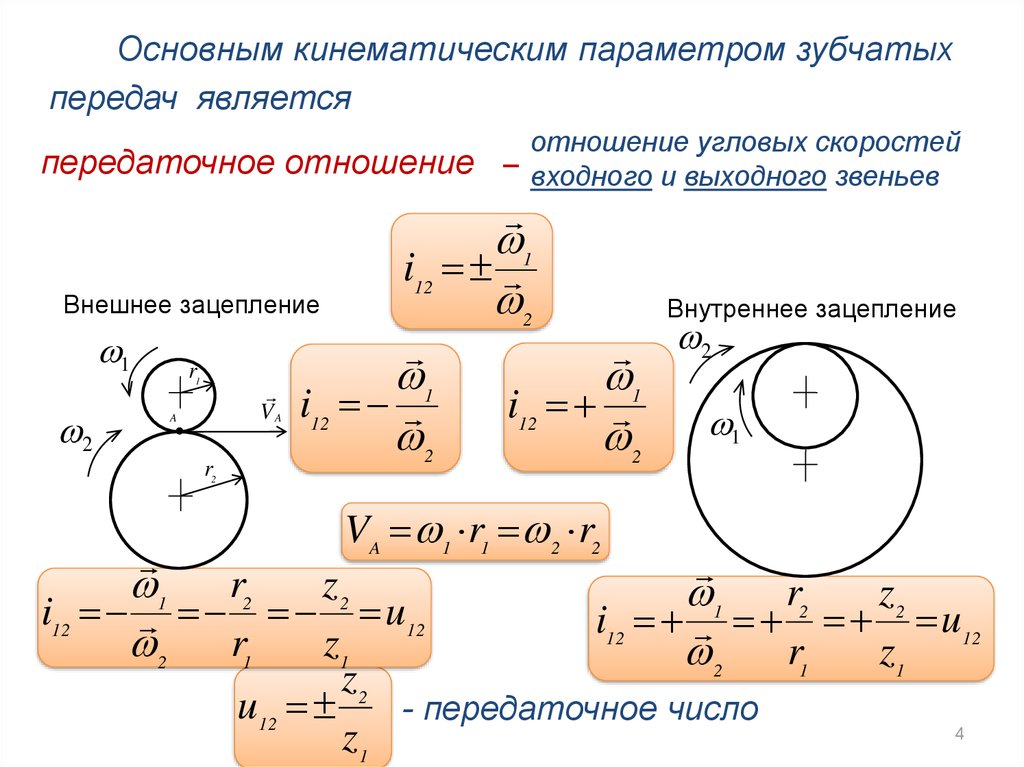
Основным кинематическим параметром зубчатых
передач является
передаточное отношение
Внешнее зацепление
1
2
r1
VA
.
A
r2
отношение угловых скоростей
– входного и выходного звеньев
1
i12
1
i12
2
2
Внутреннее зацепление
2
1
i12
1
VA 1 r1 2 r2
2
1 r2
z2
z2
1 r2
i12 u12
i12 u12
2 r1
z1
z1
2
r1
z2
u12
- передаточное число
4
z1

5.

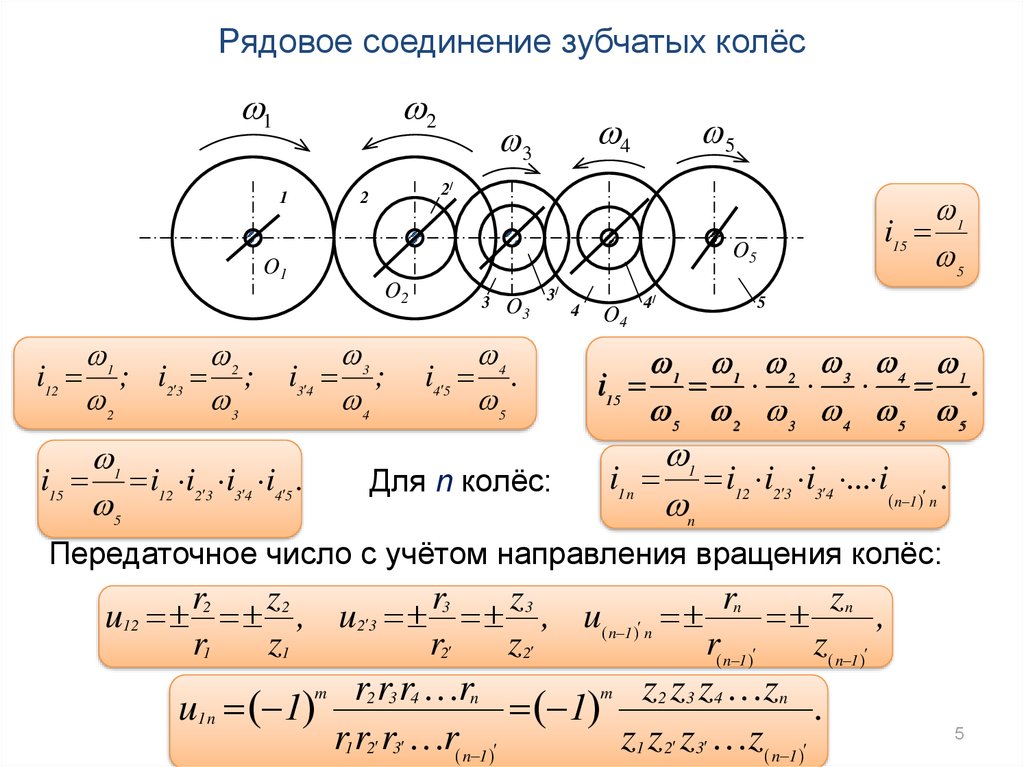
Рядовое соединение зубчатых колёс
2
1
1
1
; i2 3 2 ;
2
3
5
2/
2
1
i15
5
O5
O1
i12
4
3
O2
i3 4
1
i15 i12 i2 3 i3 4 i4 5 .
5
3
;
4
3
i4 5
O3
3/
4
.
5
Для n колёс:
4
O4
4/
5
1 1 2 3 4 1
i15 .
5 2 3 4 5 5
1
i1n i12 i2 3 i3 4 ... i .
n 1 n
n
Передаточное число с учётом направления вращения колёс:
r2
z2
r3
z3
rn
zn
u12 , u2 3 , u n 1 n
,
r1
z1
r2
z2
r n 1
z n 1
m
r2 r3 r4 rn
z2 z3 z4 zn
u1n 1
1
.
r1 r2 r3 r n 1
z1 z2 z3 z n 1
m
5

6.

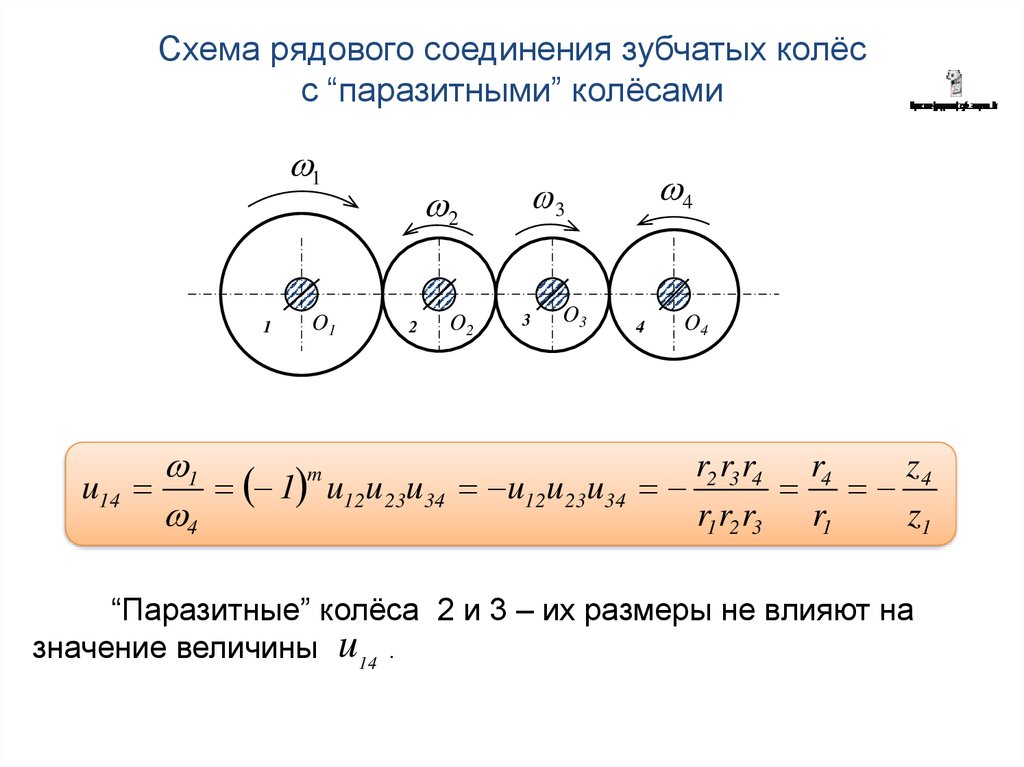
Схема рядового соединения зубчатых колёс
с “паразитными” колёсами
1
1
O1
2
O2
4
3
2
3
O3
4
O4
r2 r3 r4 r4
z4
1
m
u14
1 u12u23u34 u12u23u34
4
r1 r2 r3 r1
z1
“Паразитные” колёса 2 и 3 – их размеры не влияют на
значение величины u14 .

7.

Трехступенчатый зубчатый редуктор
4
3
2
4
5
1
1
3
u15 1 u12u23u3 4 u4 5
3
5
z 2 z3 z4 z5
zzz
3 4 5
z1 z 2 z3 z4
z1 z3 z4
Из последнего соотношения колесо 2 - “паразитное колесо”.
7

8.

Механизмы с подвижными осями
(Эпициклические механизмы)
B некоторых многоступенчатых зубчатых передачах оси
отдельных колес являются подвижными. Такие зубчатые механизмы с одной степенью свободы называются планетарными
механизмами, а с двумя и более степенями свободы —
дифференциальными механизмами или просто дифференциалами.
B этих механизмах колеса с подвижными осями вращения
называются планетарными колесами или сателлитами, а
звено, на котором располагаются оси сателлитов, — водилом.
Ha схемах водило принято обозначать буквой H. Зубчатые
колеса с неподвижными осями вращения называются солнечными или центральными; неподвижное колесо — опорным.

9.

o2
r2
O2
2
r1-r2 r2
P 2
H
2
O2
1
H
H
r1
O1
O1
1
а
б
Кинематическая схема трехзвенного планетарного механизма

10.

Связь между угловыми скоростями 2 и
может быть установлена из
H
рассмотрения рисунка. Для точки O2 скорость
O2 является общей для колеса 2 и водила H, с учетом знаков угловых скоростей
и
:
H
2
O 2 r2 H r1 r2
2
Следовательно, передаточное отношение
u2 H
(1)
u 2 H равно:
2 r2 r1
r1
1 1 u21
H
r2
r2
(2)
Из рассмотрения равенств (2) видно, что передаточное отношение u 2 H
есть передаточное отношение при неподвижном колесе 1, а передаточное
отношение
21 есть передаточное отношение трехзвенного зубчатого механизма с колесами, имеющими неподвижные оси, т. е. как бы при неподвижном
водиле H.
u

11.

B дальнейшем, чтобы знать, при каком неподвижном звене определяем
то или иное передаточное отношение, будем у передаточного отношения в
скобках ставить верхний индекс того звена, которое принято за неподвижное.
Тогда уравнение (2) перепишем так:
1
H
u2 H 1 u21
(3)
Уравнение (3) может быть представлено еще так:
u
(1)
2H
u
(H )
21
1
(4)
т. е. для планетарных механизмов с круглыми колесами сумма передаточных
отношений при различных останавливаемых звеньях всегда равна единице.

12. На рисунке показан планетарный редуктор, который носит название редуктора Давида. Передаточное отношение от вала к валу

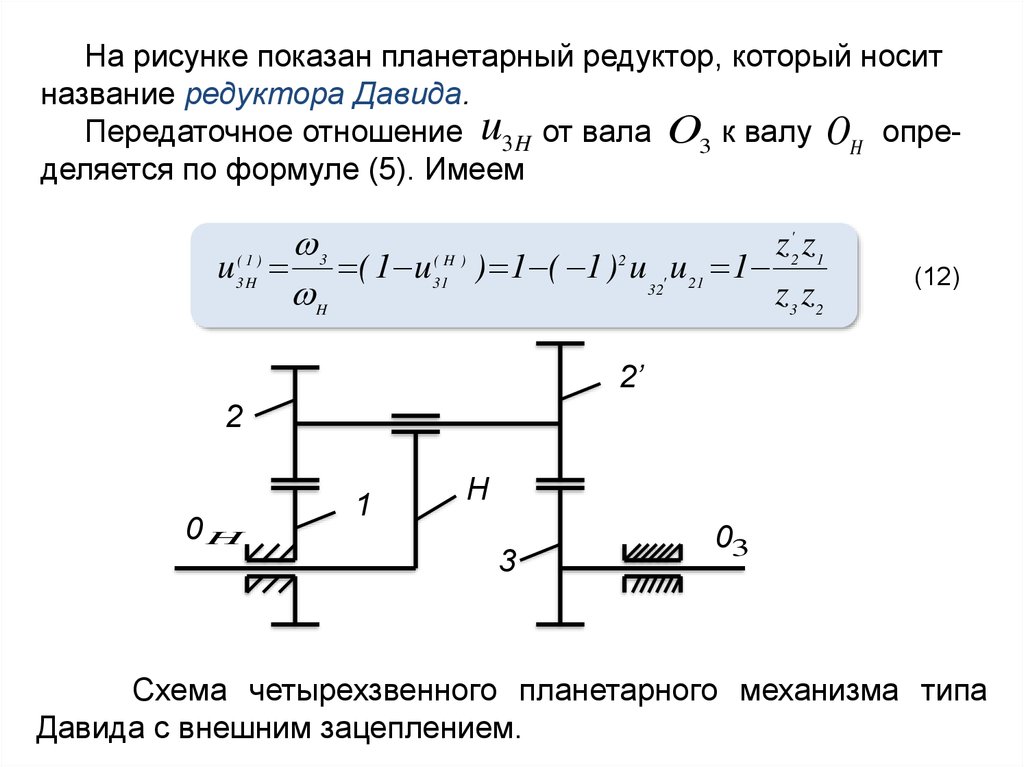
На рисунке показан планетарный редуктор, который носит
название редуктора Давида.
Передаточное отношение u3 H от вала O3 к валу OH определяется по формуле (5). Имеем
'
z
z
3
2 1
(1)
(H )
2
u3 H ( 1 u31 ) 1 ( 1 ) u ' u21 1
32
H
z3 z 2
(12)
2’
2
0H
1
H
3
03
Схема четырехзвенного планетарного механизма типа
Давида с внешним зацеплением.

13. Схема трехзвенного планетарного механизма с кони-ческими колесами

2
1
d
c
b
a
3
O3
OH
H
Схема трехзвенного планетарного механизма с коническими колесами
Редукторы Давида с малым передаточным отношением
обладают очень малым коэффициентом полезного действия.

14.

2
1
OH
2
H
3
O3
Схема четырехзвенного планетарного механизма типа
Давида с внутренним зацеплением

15. На рисунке показана модификация редуктора Давида с сател-литом, входящим в два внутренних зацепления. Передаточное отношение от

На рисунке показана модификация редуктора Давида с сателлитом, входящим в два внутренних зацепления. Передаточное
(1)
отношение u от вала O3 к валу OH может быть определено по
3H
формуле (12).
(H )
u
Так как обычно в этой модификации редуктора Давида
H3
входным является водило H, то передаточное отношение от вала
OH к валу O3 определится по формулам (9) и (12).
Имеем
u
(1)
H3
1
1
(1)
u3 H 1 z 2' z1 /( z 3 z 2 )
(13)

16. где и -соответственно числа зубьев колеса 1, 2, 2’и 3

На (рис.3.6.) показана модификация редуктора Давида с
(1)
коническими колесами. Передаточная отношение u3H
от вала O3
к валу OH определится по формуле (3.12.). Знак у
передаточного отношения u3( HH ) будет минус, так как стрелки a и d
(рис.3.4) имеют противоположные направления. Теперь
рассмотрим редуктор (рис.3.7.) смешанного вида с одним
внешним и одним внутренним зацеплением. Передаточное
(1)
отношение u3H
от вала O3 к валу OH будет равно
(1)
3H
u
3
zz
(H )
(H ) (H )
1 u31 1 ( 1)u32 ' u2 '1 1
H
z3 z 2
'
2 1
z
где z1 , z2 , z2 ' и 3 -соответственно числа зубьев колеса 1, 2, 2’и 3

17.

(1)
3H
u
3
zz
(H )
(H ) (H )
1 u31 1 ( 1)u32 ' u2 '1 1
H
z3 z 2
'
2 1
2’ b
C
d
OH
2
B
H
a
3
рис.3.6. Схема четырехзвенного планетарного механизма
типа Давида с коническими колесами

18. Схема четырехзвенного планетарного механизма с внутренним и внешним зацеплениями

2
2
1
H
OH
O3
3
Схема четырехзвенного планетарного механизма с
внутренним и внешним зацеплениями