Похожие презентации:
Статистические методы определения показателей надежности аппаратного обеспечения автоматизированных систем
1. Надежность автоматизированных систем
Раздел 1. Надежность аппаратногообеспечения автоматизированных
систем
Тема 3. Статистические методы
определения показателей надежности
аппаратного обеспечения
автоматизированных систем
Лекция
1
2. Учебные вопросы
1. Экспоненциальное (показательное) распределение2. Нормальное распределение (распределение
Гаусса)
3. Усеченное нормальное распределение
4. Логарифмически нормальное распределение
5. Распределение Вейбулла
6. Гамма-распределение
7. Равномерное распределение
8. Смесь распределений
2
3.
Показатели надежности аппаратногообеспечения АС являются
непрерывными случайными
величинами, в связи с этим для
определения их значений используется
аппарат математической статистики –
законы распределения непрерывных
случайных величин.
3
4. 1. Экспоненциальное (показательное) распределение
Экспоненциальное (показательное)распределение задается функцией:
F(t)=1-e- t при t 0.
Экспоненциальным законом
распределения можно аппроксимировать
время безотказной работы большого числа
систем.
4
5.
Это распределение имеет один параметр1 , где Т - средняя наработка
1
Т1
до отказа.
Таким образом, параметр характеризует
число отказов элемента в единицу
времени, называется интенсивностью
отказов и имеет размерность 1/время.
5
6.
Плотность экспоненциальногораспределения задается следующим
образом:
f(t)= e- t.
Вероятность безотказной работы за
время t (функция надежности)
определяется с помощью выражения:
P(t)=e- t.
6
7.
Рис. 1. Функция надежности P(t)=e- t при =0,02 час-17
8.
Экспоненциальное распределениевыделяется среди других распределений
свойством «отсутствия памяти», которое
означает, что система, проработавшая время
t, имеет такое же распределение, что и новая,
только начавшая работу.
Данное свойство как бы исключает износ и
«старение» системы.
8
9.
Числовые характеристикиэкспоненциального распределения
выражаются через его параметр:
1
математическое ожидание М ( Х ) ;
1
дисперсия D( Х ) 2 ;
среднее квадратическое отклонение
1 .
( Х )
9
10.
Итак, при экспоненциальномраспределении между показателями
надежности системы существуют
следующие зависимости:
P(t)=e- t,
1
, f(t)= e- t.
T1
10
11. 2. Нормальное распределение (распределение Гаусса)
Нормальное распределение определяетсяплотностью
1
f (t )
e
2
( t m )2
2 2
, t
и зависит от двух параметров m и , которые
являются соответственно математическим
ожиданием и среднеквадратическим
отклонением времени безотказной работы
системы.
11
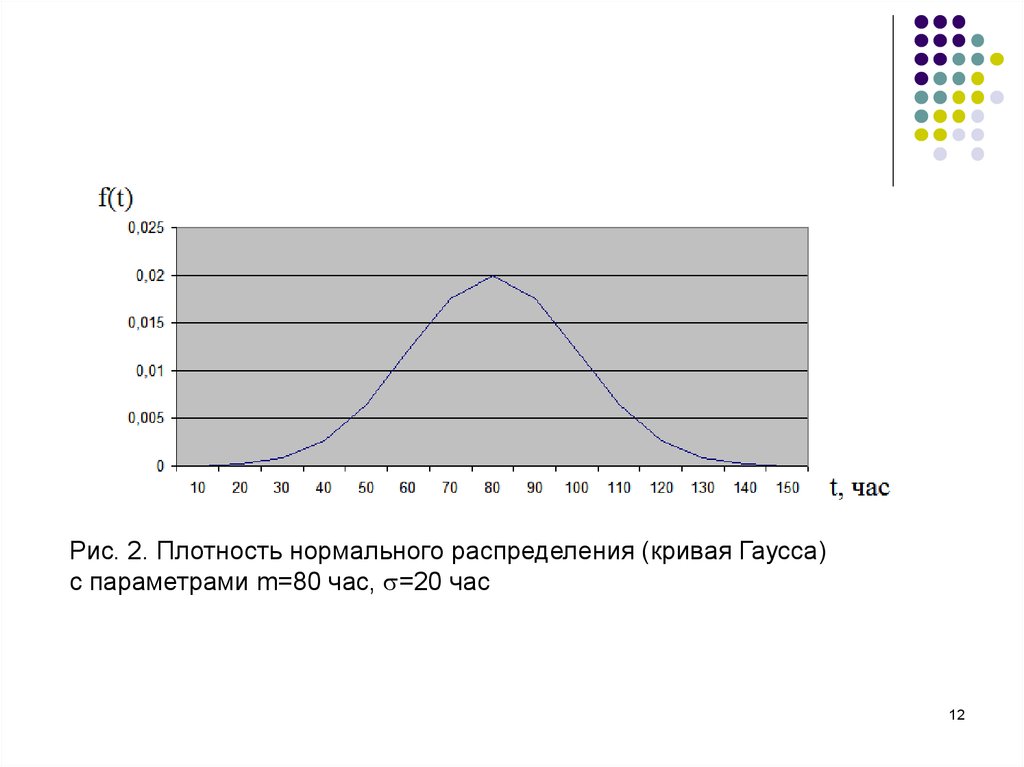
12.
Рис. 2. Плотность нормального распределения (кривая Гаусса)с параметрами m=80 час, =20 час
12
13.
Согласно закону больших чисел, распределениевсегда подчиняется нормальному закону, если на
изменение случайной величины оказывают
влияние многие примерно равнозначные факторы.
Для нормального распределения функция
надежности вычисляется по формуле:
1
P(t )
e
t 2
где
( x m )2
2 2
x2
2
t m
dx 0,5 Ф0 (
)
1
Ф0 (t )
e dx
2 0
t
- функция Лапласа,
значения которой сведены в таблицы.
13
14. 3. Усеченное нормальное распределение
Усеченное нормальное распределение получается изнормального при ограничении интервала изменения
случайной величины на промежуток [0,+ ].
Плотность распределения записывается так же, как
для нормального распределения, но с
коэффициентом пропорциональности с:
f (t )
c
0 2
e
( t m0 ) 2
2 0 2
14
15.
Усеченное нормальное распределениезависит от двух параметров m0 и 0,
где m0 - значение случайной величины,
соответствующее максимальному значению
f(t), называемое модой.
Коэффициент с определяется из условия
нормировки:
f (t )dt 1
0
c
откуда
1
,
m0
0,5 Ф0
0
15
16.
Математическое ожидание исреднеквадратическое отклонение
усеченного нормального распределения
определяются через параметры m0 и 0 по
формулам:
m
m m0 k 0 ,
0 1 k 0 k 2 ,
где
c
k
e
2
m02
2
2 0
0
.
16
17. 4. Логарифмически нормальное распределение
В логарифмически нормальномраспределении логарифм случайной
величины подчиняется нормальному
закону с плотностью
1
f (t )
e
st 2
(ln t )2
2 s2
,
где и s - параметры распределения.
17
18.
Математическое ожидание исреднеквадратическое отклонение
определяются в соответствии с
формулами:
m e
2 s
2
e
2 s 2
s2
(e 1)
,
.
Логарифмически нормальное
распределение применяют для описания
случайных величин, представляющих
собой произведение достаточно большого
числа случайных величин.
18
19. 5. Распределение Вейбулла
Распределение Вейбулла является достаточноуниверсальным, благодаря возможности
варьирования двух параметров. Характеризуется
плотностью распределения:
1
t
f (t ) e
t
с параметром формы и параметром масштаба
.
19
20.
Математическое ожидание и среднееквадратическое отклонение выражаются
следующим образом:
1 ,
2
1
,
2
Г (1 ) Г (1 )
m Г (1 )
где
Г (t ) xt 1e x dx - гамма-функция.
0
20
21.
Универсальность распределения Вейбуллаобъясняется следующим:
при =1 оно превращается в
экспоненциальное;
при <1 функции плотности и интенсивности
отказов убывающие;
при >1 интенсивность отказов
возрастающая;
при =3,3 распределение близко к
нормальному.
21
22.
Зависимости между показателяминадежности имеют вид:
P(t ) e
t
1
T1 Г (1 )
1
t
,
,
.
22
23.
Рис. 3. Графики интенсивности отказов для распределения Вейбуллапри разных параметрах: ряд 1 - =2 и =200 час; ряд 2 - =3 и =200 час
23
24.
При =2 функция (t) линейная ираспределение Вейбулла превращается в
распределение Рэлея с плотностью
f (t ) 2 te
t
2
.
24
25. 6. Гамма-распределение
Гамма-распределение имеетплотность
t
t 1
f (t )
e
Г ( )
с параметрами и .
Математическое ожидание и среднее
квадратическое отклонение связаны с
этими параметрами следующим образом:
m , .
25
26.
Вероятность безотказной работыэлемента определяется через интеграл:
1
x
x
P(t )
e dx .
t Г ( )
26
27.
Параметр , характеризующийасимметрию гамма-распределения,
определяет вид характеристик
надежности.
При >1 интенсивность отказа возрастает,
при <1 - убывает, а при =1 становится
постоянной, т.е. гамма-распределение
превращается в экспоненциальное.
27
28. Рис. 4. Плотность распределения времени до отказа при гамма-распределении
2829. Рис. 5. График вероятности безотказной работы системы при гамма-распределении времени работы до отказа
2930. 7. Равномерное распределение
Непрерывное равномерноераспределение — распределение СВ,
принимающей значения, принадлежащие
интервалу [a,b], характеризующееся тем,
что плотность вероятности на этом
интервале постоянна.
30
31.
Плотность непрерывногораспределения имеет вид:
1
, a t b;
f (t ) b a
.
0, t a, t b
31
32.
Вероятность безотказной работыопределяется следующим образом:
1, t a;
b t
P(t )
, a t b;
b a
0, t b.
32
33.
Математическое ожидание исреднеквадратическое отклонение
связаны с параметрами a и b следующим
образом:
a b
m
2 , (совпадает с серединой
b a
отрезка)
2 3
.
33
34. Рис. 6. График плотности распределения времени до отказа при равномерном распределении
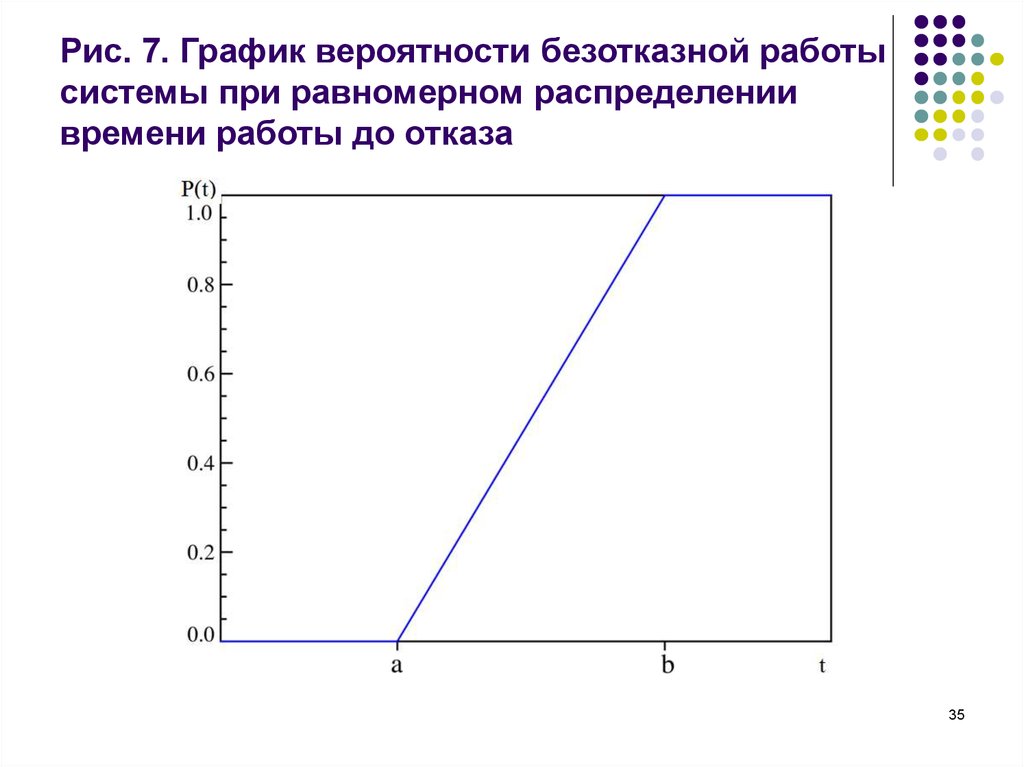
3435. Рис. 7. График вероятности безотказной работы системы при равномерном распределении времени работы до отказа
3536. 8. Смесь распределений
Смесь распределений определяется каклинейная комбинация других
распределений, например, распределение
с плотностью
n
f (t ) ci i e
n
it
i 1
ci 1
где i 1
образует смесь n
экспоненциальных распределений.
Такое распределение называется
гиперэкспоненциальным.
36
37. Таблица 1 Связь параметров распределений с математическим ожиданием и средним квадратическим отклонением
3738. Таблица 2 Вероятность безотказной работы и плотность распределения времени до отказа для различных распределений случайной
величины38
39.
Примечание. Равномерное и нормальноераспределения имеют ограничения на
параметры для того, чтобы можно было их
использовать для решения задач
надежности в неотрицательной временной
области (t 0).
39





































 Промышленность
Промышленность








