Похожие презентации:
Проектировочный расчет закрытой зубчатой передачи
1. Домашнее задание по курсу «Детали машин» №2
«Проектировочный расчетзакрытой зубчатой передачи»
2. 1. Выбор материала для шестерни и зубчатого колеса редуктора
Нагружение шестерни больше, чем у зубчатого колеса, т.к. числоциклов нагружений зубьев шестерни больше, чем у колеса, поэтому
твердость шестерни должна быть выше твердости зубчатого колеса
на 20 - 50 единиц.
HB 1 НВ 2 20 50 ,
Материалы и термообработку
стандартами по таблицам.
Н
мм 2
назначают
в
соответствии
со
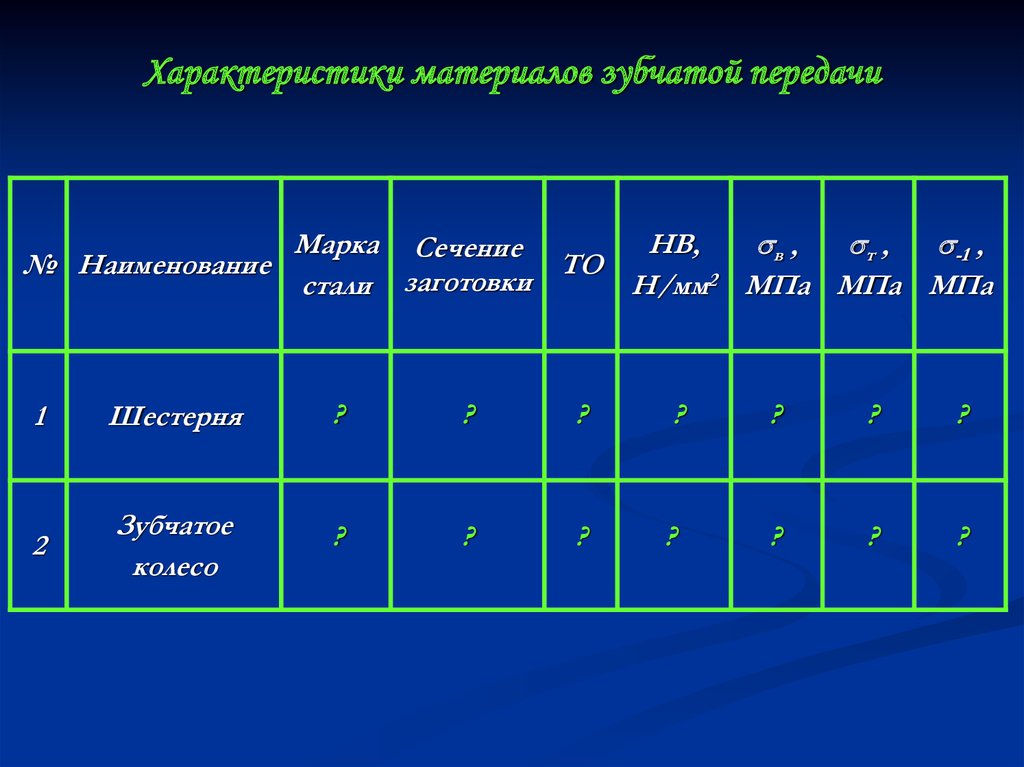
3. Характеристики материалов зубчатой передачи
Марка СечениеНВ,
в ,
т ,
-1 ,
№ Наименование
ТО
стали заготовки
Н/мм2 МПа МПа МПа
1
Шестерня
?
?
?
?
?
?
?
2
Зубчатое
колесо
?
?
?
?
?
?
?
4. 2. Определение коэффициента долговечности:
k HD ?2.1. Рассчитываем эквивалентное число циклов контактных напряжений:
N HE эквивалентным называют некоторое расчетное число циклов,
которое при действии постоянной нагрузки, равной максимальной
нагрузке рассчитываемой передачи, дало бы тот же эффект по
пределу выносливости рабочих поверхностей зубьев, который дает
в течение фактического числа циклов действительная переменная
нагрузка передачи.
N HE1 60 n1 t 0 ( 13 k 1 23 k 2 33 k 3 ) .... 10 7 , циклов
N HE 2
N HE 1
... 10 7 , циклов
u
5. 2.2. Рассчитываем базовое число циклов контактных напряжений:
N HO базовое число циклов контактных напряжений до перегибакривой усталости (гиперболы), соответствующее длительному
пределу выносливости при контактных напряжениях.
2 ,4
... 10 7 , циклов
2 ,4
... 10 7 , циклов
N HO1 30 HB 1
N HO2 30 HB 2
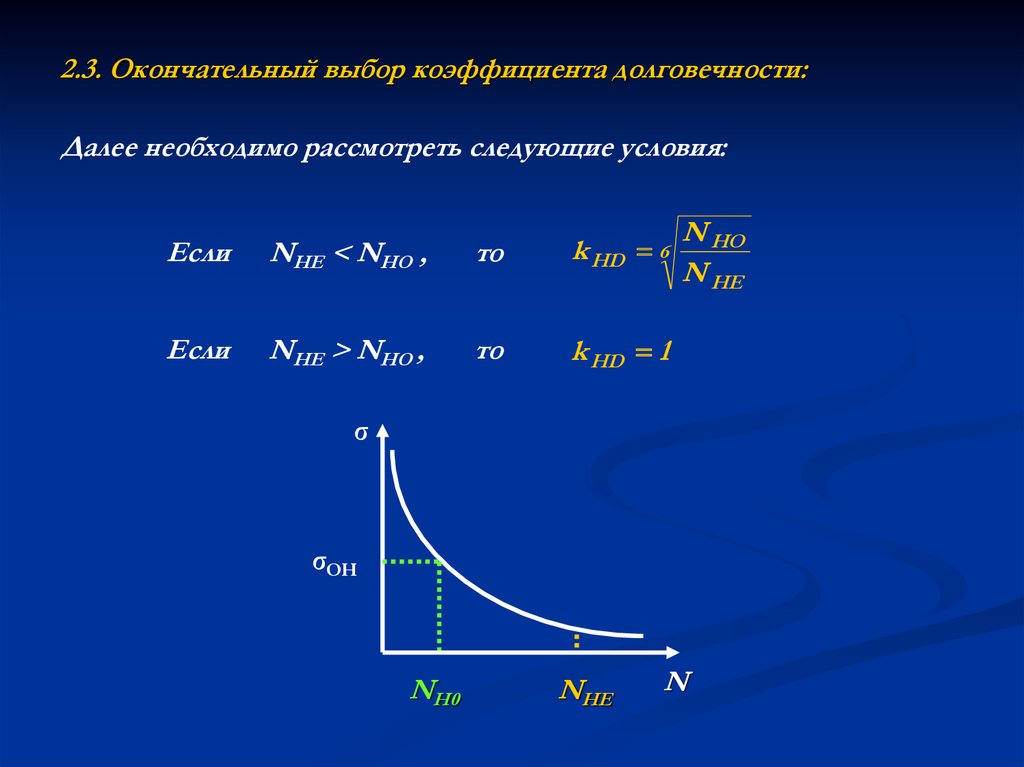
6. 2.3. Окончательный выбор коэффициента долговечности:
Далее необходимо рассмотреть следующие условия:Если
NHE < NHO ,
то
k HD 6
Если
NHE > NHO ,
то
k HD 1
N HO
N HE
σ
σОН
NН0
NНE
N
7. 3. Определение допускаемых контактных напряжений:
НH lim b Z R N H 0
6
SH
N HE
H limb - предел контактной выносливости для зубьев колеса и шестерни,
формула выбирается из таблицы в соответствии с маркой материала,
термообработкой и твердостью материала:
H lim b1 2 HB 1 70 ... МПа
H lim b2 2 HB 2 70 ... МПа
8.
ZR = 1 - коэффициент, учитывающий шероховатость поверхности;SH = 1,1 – коэффициент безопасности для объемно упрочненных зубьев;
k HD 6
N HO
1 – коэффициент долговечности.
N HE
H lim b1
H1
... МПа
SH
H 2
H lim b2
... МПа
SH
для прямозубых колес за допускаемое контактное напряжение берут
меньшее значение H ;
для косозубых и шевронных колес за допускаемое контактное
напряжение берут H = 0,45(σН1 + σН2).
[ H ]= … МПа
9. 4. Определение коэффициента нагрузки при расчете на контактную выносливость:
Так как на данном этапе нам не известны параметры зубчатогозацепление, то мы выбираем коэффициент нагрузки из следующего
интервала:
кн= (1,3 – 1,5)
кн= 1,3
10. 5. Определение межосевого расстояния:
2aW
'
K
T
P
u 1 3
... , мм
3
u
H
a 10
к = 270 – для косозубых передач;
к = 315 – для прямозубых передач;
u – передаточное число, выбирается из стандартного ряда (домашнее
задание №1);
ψа=0,315 – коэффициент ширины колеса, для симметричного
расположения;
TP' T2 k HD k H – расчетный момент, Н м.
11.
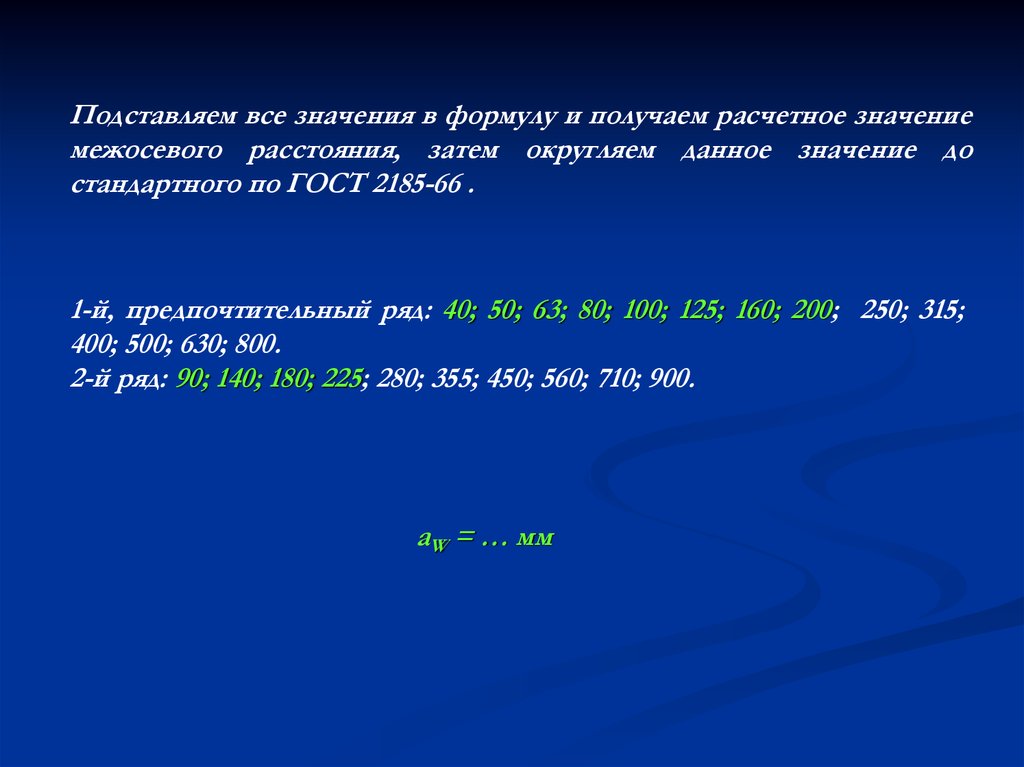
Подставляем все значения в формулу и получаем расчетное значениемежосевого расстояния, затем округляем данное значение до
стандартного по ГОСТ 2185-66 .
1-й, предпочтительный ряд: 40; 50; 63; 80; 100; 125; 160; 200; 250; 315;
400; 500; 630; 800.
2-й ряд: 90; 140; 180; 225; 280; 355; 450; 560; 710; 900.
аW = … мм
12. 6. Определение основных параметров зубчатого зацепления:
6.1. Определение типа передачи (по скорости):aW u n 2
м
V
,
u 1 30 1000 с
V ≤ 3,5
м - применяем прямозубые передачи;
с
V >3,5
м - применяем косозубые передачи.
с
Если предварительное допущение о виде передачи неверно, находим
межосевое расстояние применяя иной коэффициент и продолжаем
расчет геометрических параметров.
13. 6.2. Определение модуля зацепления:
mn 0 ,01 0 ,02 aW ... , ммСтандартные значения: 2; 2,25; 2,5; 2,75; 3; 3,5; 4; 4,5; 5.
mn= … ,мм
6.3. Определяем угол наклона зубьев:
Угол наклона зубьев для косозубой передачи выбирают в пределах =8 18 0
Угол наклона зубьев прямозубой передачи =0 0
14. 6.4. Определение числа зубьев шестерни и колеса:
2 aW cosmn
zC
z1
u 1
zC z 1 z 2
z 2 z 1 u
Округляем полученные результаты до целых значений, числа зубьев не
могут быть дробными.
Проверяем расчет:
zc z1 z 2
15. 6.5. Уточняем угол наклона :
6.5. Уточняем угол наклона :mn z C
2 aW
arccos
6.6. Определяем торцовый модуль зацепления:
Модуль торцевой определяют через уточненный угол наклона, мм:
mn
mt
cos
16. 6.7. Определяем ширину зубчатого колеса и шестерни, мм:
b 2 a aWb1 b2 5 мм
6.8. Определяем диаметры делительных окружностей шестерни и
колеса, с точностью до сотых долей, мм:
d 1 z 1 mt
d 2 z 2 mt
При расчете прямозубой передачи используют модуль нормальный mn.
После расчета делительных окружностей делают проверочный расчет:
aW
d1 d 2
2
17. 6.10. Расчет размеров зубьев для зубчатого колеса и шестерни:
Высота головки зуба, мм:ha mn
Высота ножки зуба, мм:
hf 1 , 25 mn
Высота зуба, мм:
h ha hf
18. 6.11. Расчет диаметров выступов и впадин зубчатого колеса и шестерни:
Диаметр вершин, мм:d a2 d 2 2 ha d 2 2 m n
d a1 d 1 2 ha d 1 2 mn
Диаметр впадин, мм:
d f 2 d 2 2 hf d 2 2 ,5 m n
d f 1 d 1 2 hf d 1 2 ,5 m n
19. 6.12. Расчет угловых скоростей:
1n1 рад
,
30
с
2
n 2 рад
,
30
с
Уточняем передаточное число, разница между выбранным
стандартным
значением
передаточного
числа
и
полученным не должна быть больше 2% :
u
z2 d2 1
z1 d1 2
20.
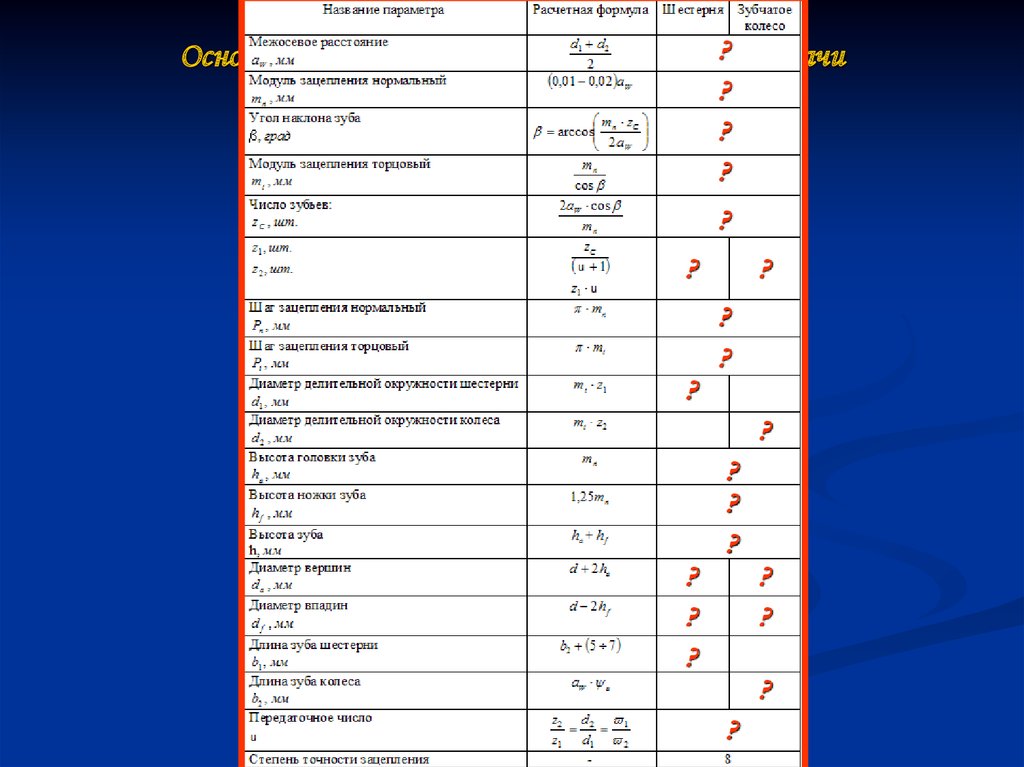
21. Основные параметры закрытой зубчатой передачи
Основные параметры закрытой зубчатой? передачи?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
22. 7. Проверочный расчет тихоходной ступени:
Проверочный расчет выполняется для тихоходной ступени, какнаиболее нагруженной.
7.1. Проверка зубьев на выносливость по контактным напряжениям:
H k
u 1 u 1
T p 10 3
aW u b2
T p T 2 k HD k H – расчетный момент, Н м
23. 7.2. Уточняем коэффициент нагрузки:
k H k H k H k HVКНα – коэффициент распределения нагрузки между зубьями;
КНα = 1 - для прямозубых колес.
Значение КНα для косозубых и шевронных передач определяем из
таблицы:
Окружная
скорость
V, м/с
Степень точности по нормам плавности (ГОСТ 1643-81)
5
6
7
8
9
2,5
1,00
1,01
1,03
1,05
1,13
5
1,00
1,02
1,05
1,09
1,16
24. КНβ – коэффициент концентрации нагрузки по ширине венца зубчатого колеса выбираем из таблицы:
Расположениезубчатых колес
относительно опор
Твердость НВ поверхностей зубьев
≤ 350
> 350
Симметричное
1,0…1,15
1,05…1,25
Несимметричное
1,10…1,25
1,15…1,35
Консоль
1,20…1,35
1,25…1,45
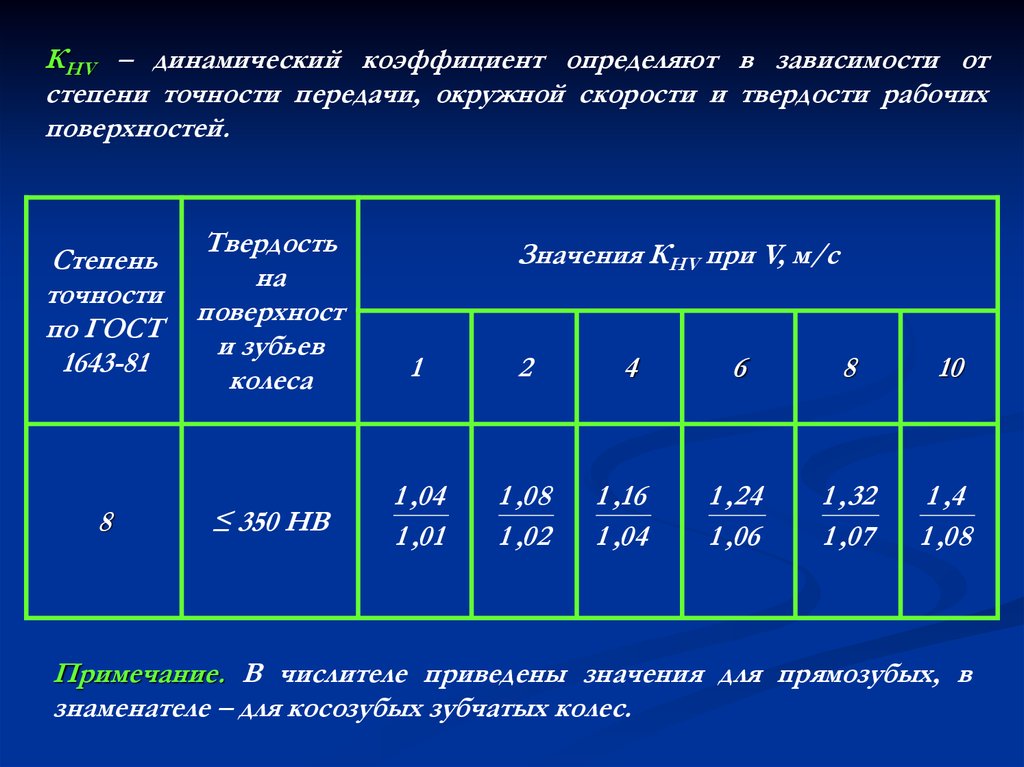
25. КНV – динамический коэффициент определяют в зависимости от степени точности передачи, окружной скорости и твердости рабочих
поверхностей.Степень
точности
по ГОСТ
1643-81
8
Твердость
на
поверхност
и зубьев
колеса
1
2
4
6
8
10
≤ 350 НВ
1 ,04
1 ,01
1 ,08
1 ,02
1 ,16
1 ,04
1 , 24
1 ,06
1 , 32
1 ,07
1 ,4
1 ,08
Значения КНV при V, м/с
Примечание. В числителе приведены значения для прямозубых, в
знаменателе – для косозубых зубчатых колес.
26. 7.3. Рассчитываем отклонение величины действительного контактного напряжения от допускаемого:
7.3.Рассчитываем
отклонение
величины
контактного напряжения от допускаемого:
H
действительного
H H
100% 5%
H
По принятым в общем машиностроении нормам для σН допускается
отклонение ± 5%. Если отклонения выходят за указанные пределы, то
размеры и другие параметры передачи необходимо откорректировать.
При больших отклонения порядка ± 10…15% можно рекомендовать:
в небольших пределах изменить ширину колеса b2 (при перегрузках –
увеличить, при недогрузках – уменьшить).






















 Механика
Механика








