Похожие презентации:
Меры связи, основанные на статистической зависимости. Коэффициент Юла
1. Меры связи, основанные на статистической зависимости. Коэффициент Юла
Курс «Анализ социологических данных», магистратура, 1 г.о.© Пузанова Ж.В., 2017
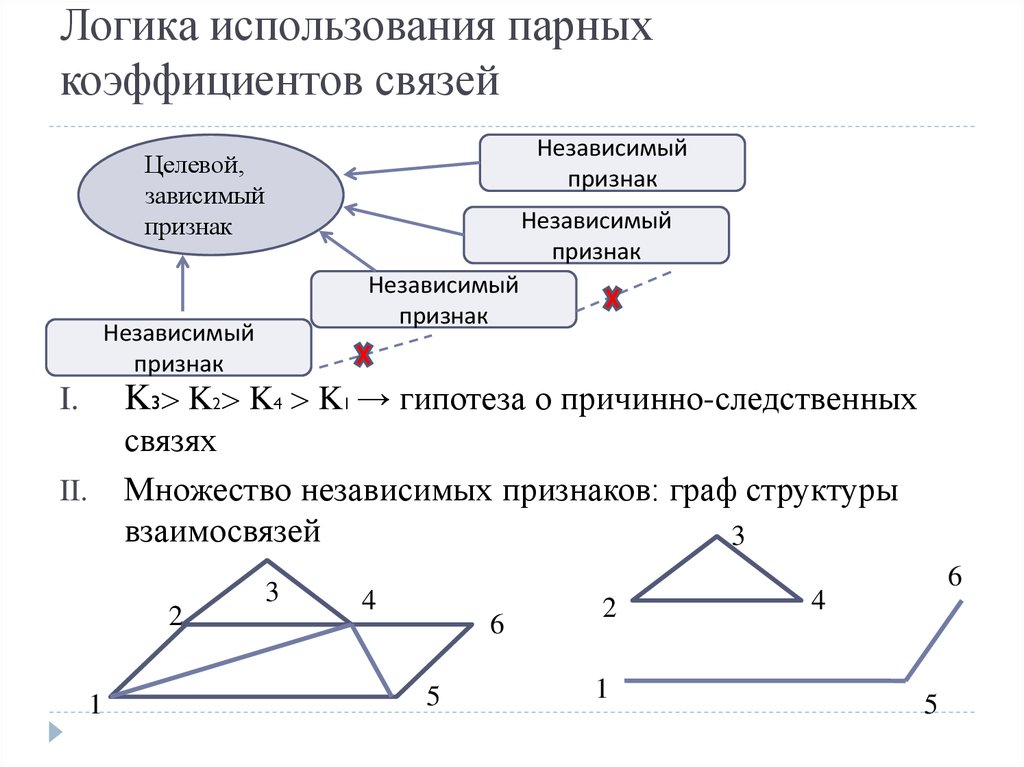
2. Логика использования парных коэффициентов связей
Независимыйпризнак
Целевой,
зависимый
признак
Независимый
признак
Независимый
признак
Независимый
признак
I.
K3 K2 K4 K1 → гипотеза о причинно-следственных
II.
связях
Множество независимых признаков: граф структуры
взаимосвязей
3
2
1
3
4
6
5
2
1
6
4
5
3. Анализ данных в таблицах сопряженности 2х2 Например: опрошены студенты социологи
Уверены вустройстве
на работу
Не уверенны
в устройстве
на работу
Итого
Магистры
15 (a)
35 (d)
50
Бакалавры
Итого
110 (c)
125
340 (b)
375
450
500
Коэффициент
Юла:
Есть ли статистическая закономерность между этими признаками?
Если наблюдается статистическая независимость, то …
доля магистров в группе «уверенных» должна равняться доле магистров в группе
«неуверенных», т.е.
, т.е.
a (d+b) = (a+c) d → ab = cd ; и a (c + b) = (a + d) c → ab = cd
ab - cd - мера отклонения от статистической независимости;
Знаменатель – для нормирования (изменения от – 1 до + 1)
4. Свойства коэффициента Юла:
УН
Маг
a
d
Бак
c
b
Q = 1, если с = 0 или d = 0
Q = - 1, если а = 0 или b = 0
Q = 0, если ab = cd,
т.е. наблюдается статистическая независимость
Q = 0,1397 ~ 0,14
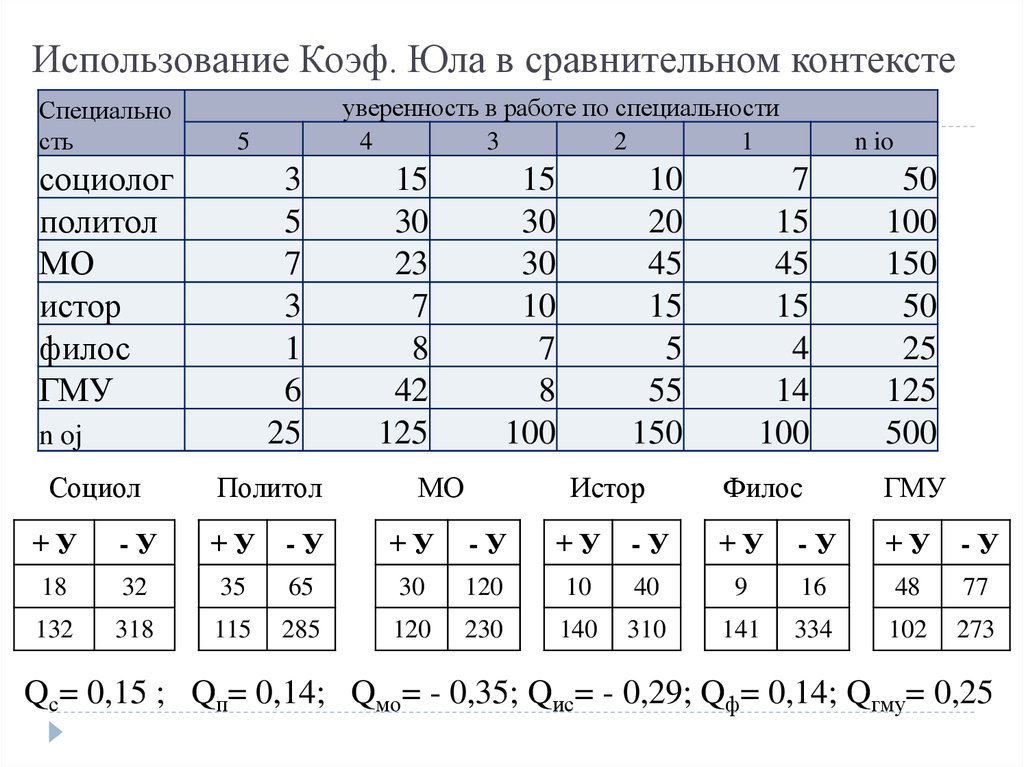
5. Использование Коэф. Юла в сравнительном контексте
Специальность
5
социолог
политол
МО
истор
филос
ГМУ
3
5
7
3
1
6
25
n oj
Социол
уверенность в работе по специальности
4
3
2
1
Политол
15
30
23
7
8
42
125
15
30
30
10
7
8
100
МО
10
20
45
15
5
55
150
Истор
n io
7
15
45
15
4
14
100
50
100
150
50
25
125
500
Филос
ГМУ
+У
-У
+У
-У
+У
-У
+У
-У
+У
-У
+У
-У
18
32
35
65
30
120
10
40
9
16
48
77
132
318
115
285
120
230
140
310
141
334
102
273
Qс= 0,15 ; Qп= 0,14; Qмо= - 0,35; Qис= - 0,29; Qф= 0,14; Qгму= 0,25
6. Сравнение по коэффициенту:
Qс= 0,15 ;Qп= 0,14;
Qмо= - 0,35;
Qис= - 0,29;
Qф= 0,14;
Qгму= 0,25
Коэффициенты упорядочиваются по силе связи (без учета
прямая или обратная зависимость), т.о.:
Qмо Qис Qгму Qс Qп Qф
Связь (в данном контексте) – статистическая зависимость
7. Понятие детерминации для локальной связи
Если А, то В - правило детерминации:одно свойство оказывает влияние на другое: А → В.
Например: Социолог → Уверенность в работе.
Характеристики детерминации:
Интенсивность :
Для социологов: а = 18; a + d = 50; a + c = 150
I (C →У) = 36 %, С (С→ У) = 12 %
Интерпретация детерминации (схема):
Емкость:
+У
-У
18
32
132
318
Интенсивность
I~0
I ~1
I~0
I~1
Емкость
C~0
C~0
C~1
C~1
Детерминация
Неточная и
неполная
Точная, но
неполная
Неточная, но
полная
Точная ,
полная
8. Непосредственная – опосредованная связь
Qс= 0,15 – указывает статистическую независимостьдля всех
для девушек
+У -У
для юношей
+У -У
+У -У
С
18
32
50
С
12
8
20
С
6
24
30
НС
132
318
450
НС
12
234
246
НС
120
84
204
150
350
500
24
242
266
126
108
234
Qс= 0,15 – ложное отсутствие корреляционной связи
6
1
5
3
2
4
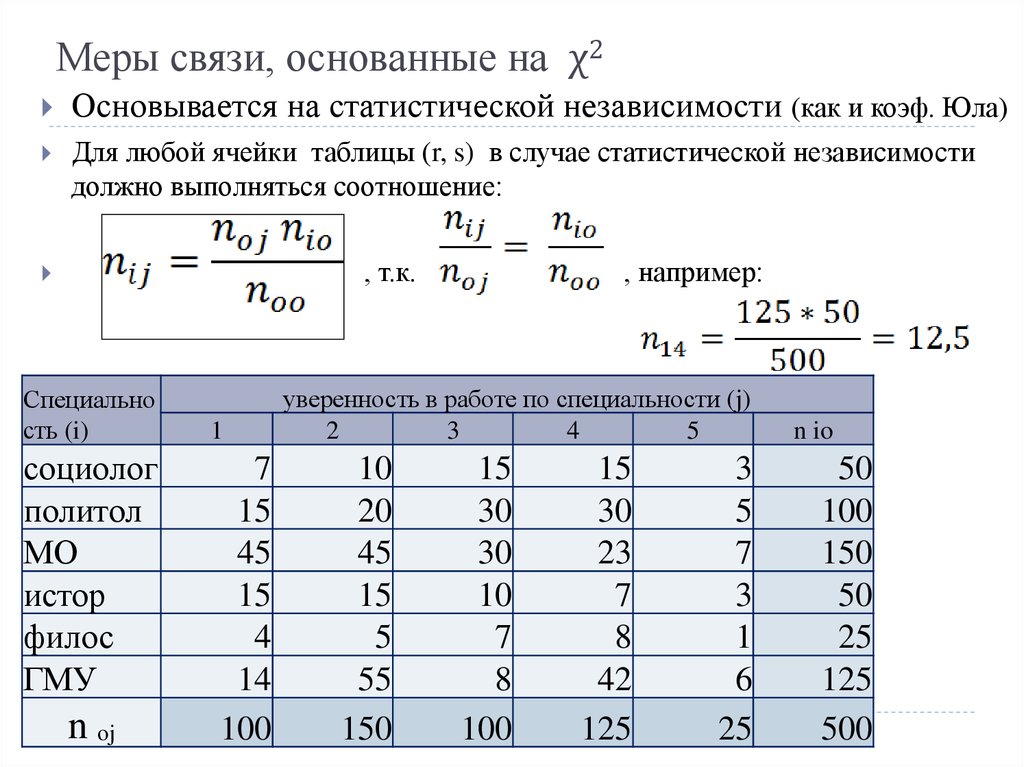
9. Меры связи, основанные на χ2
Основывается на статистической независимости (как и коэф. Юла)Для любой ячейки таблицы (r, s) в случае статистической независимости
должно выполняться соотношение:
, т.к.
Специально
сть (i)
социолог
политол
МО
истор
филос
ГМУ
n oj
1
7
15
45
15
4
14
100
, например:
уверенность в работе по специальности (j)
2
3
4
5
10
20
45
15
5
55
150
15
30
30
10
7
8
100
15
30
23
7
8
42
125
3
5
7
3
1
6
25
n io
50
100
150
50
25
125
500
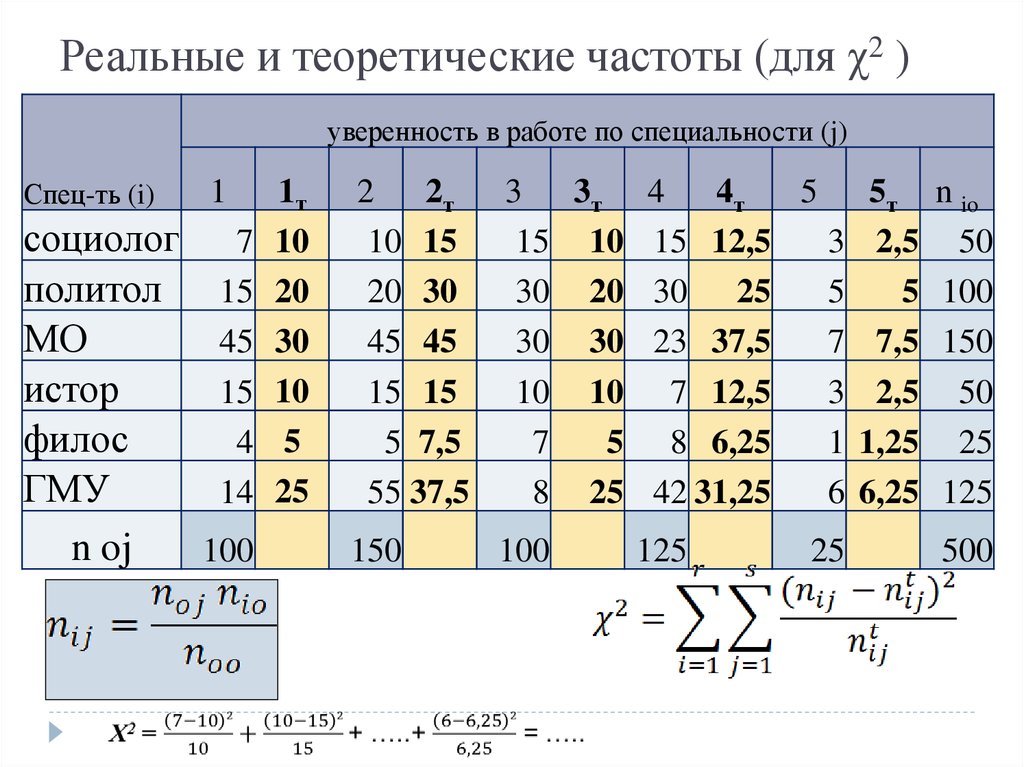
10. Реальные и теоретические частоты (для χ2 )
уверенность в работе по специальности (j)Спец-ть (i)
1
социолог 7
политол 15
МО
45
истор
15
филос
4
ГМУ
14
n oj
100
1т
10
20
30
10
5
25
2 2т
10 15
20 30
45 45
15 15
5 7,5
55 37,5
3 3т 4 4т
5 5т n io
15 10 15 12,5
3 2,5 50
30 20 30 25
5
5 100
30 30 23 37,5
7 7,5 150
10 10 7 12,5
3 2,5 50
7
5 8 6,25
1 1,25 25
8 25 42 31,25
6 6,25 125
150
100
125
25
500
11. Коэффициент взаимной сопряженности Пирсона (на основе критерия Χ2)
Χ2t – табличное значение коэффициента (находим потаблице, при заданном уровне значимости (возможной
ошибки =0,1; 0,05;0,01) и числе степеней свободы (r-1)
(s-1) (где r – число строк, s – число столбцов в таблице)
ВЫВОД о статистической значимости: Если χ2 χ2t при
заданном уровне значимости (возможной ошибки =0,1;
0,05;0,01) и числе степеней свободы (r-1) (s-1) – признаки
являются статистически зависимыми…
Наиболее часто используемый коэффициентов на основе
распределения χ2 :
С – приближается к 0 или 1
12. Домашнее задание (на любом примере из исследования практикума):
Выявить локальные связи на основе использованиякоэффициента Юла. Описать результаты
Вычислить интенсивность и емкость детерминации
для нескольких свойств (в этом же примере). Описать
результаты.
Вычислить значение хи-квадрат и сравнить с
табличным при различных уровнях значимости
(НАЙТИ ТАБЛИЦУ ХИ-КВАДРАТ САМОСТОЯТЕЛЬНО).
Описать результаты
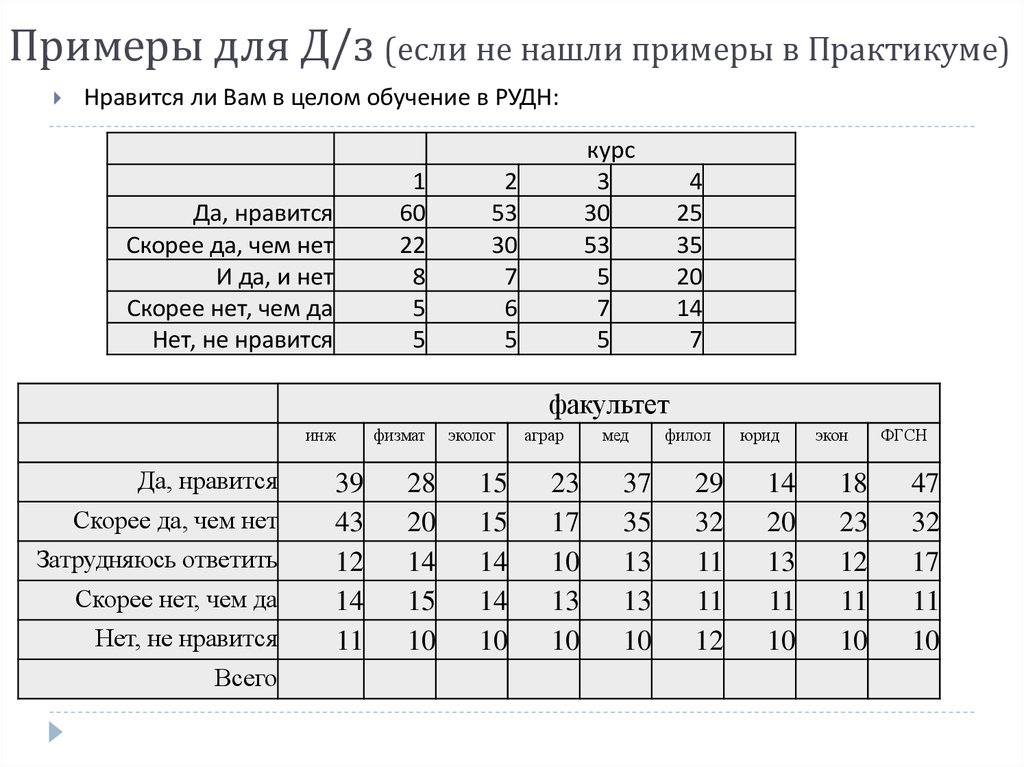
13. Примеры для Д/з (если не нашли примеры в Практикуме)
Нравится ли Вам в целом обучение в РУДН:1
60
22
8
5
5
Да, нравится
Скорее да, чем нет
И да, и нет
Скорее нет, чем да
Нет, не нравится
курс
3
30
53
5
7
5
2
53
30
7
6
5
4
25
35
20
14
7
факультет
инж
Да, нравится
Скорее да, чем нет
Затрудняюсь ответить
Скорее нет, чем да
Нет, не нравится
Всего
39
43
12
14
11
физмат
28
20
14
15
10
эколог
15
15
14
14
10
аграр
23
17
10
13
10
мед
37
35
13
13
10
филол
29
32
11
11
12
юрид
14
20
13
11
10
экон
18
23
12
11
10
ФГСН
47
32
17
11
10








 Социология
Социология








