Похожие презентации:
Статистическое изучение взаимосвязи социальноэкономических явлений
1. Тема
Статистическое изучениевзаимосвязи социальноэкономических явлений
2. Методы изучения взаимосвязи
1.2.
3.
4.
Графический
Параллельных данных
Корреляционный анализ
Регрессионный анализ
3. 1. по степени причинно-следственной определенности
Функциональная–
значение
результативного признака «у» полностью
определяется
значением
факторного
признака «х».
Корреляционная
–
значение
результативного признака «у» в большей
или
меньшей
степени
определяется
значением факторного признака «х»; при
этом имеет место влияние прочих,
неучтенных, факторов.
4. 2. По направлению:
-Прямая
Обратная
5. 3. По аналитическому выражению:
- Линейная- Нелинейная
6. 4. По количеству факторных признаков:
- Парная- Множественная
7. Графический анализ взаимосвязи
Исходные данные для построения поля корреляции(точечной диаграммы)
№ единицы
совокупности
Значения
факторного
признака
Значения
результативного
признака
1
2
3
x1
x2
x3
y1
y2
y3
n
xn
yn
Каждая единица совокупности представлена на
приведенных ниже диаграммах в виде отдельной точки.
Совокупность точек формирует графический образ.
8.
Линейная зависимостьа) прямая
б) обратная
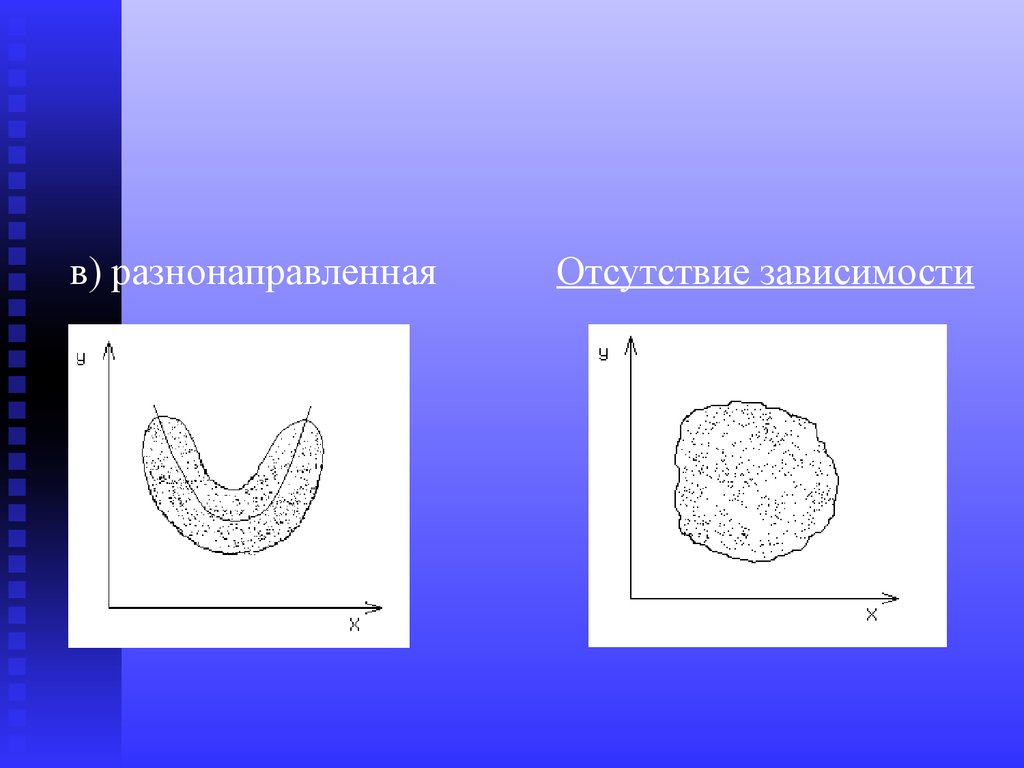
9.
Нелинейная зависимостьа) прямая
б) обратная
10.
в) разнонаправленнаяОтсутствие зависимости
11. Парная линейная зависимость
yna0x0 xa ya1x 1x2y
01
x
Парная линейная зависимость
12. Парный линейный коэффициент корреляции Пирсона
xy
x
y
r
x
y
x
y
y
x
y
x
y
x
yx
x
n
n
n
2
2
2
2
1
x
xy
1
y
y
yr
Парный линейный коэффициент
корреляции Пирсона
13.
r0,53 xyrxxx0yyy ,30,75
- очень слабая связь,
практически отсутствует
- связь слабая
- связь средняя
- связь тесная
14.
Например по данным о стоимости основныхфондов и объеме произведенной продукции
оцените тесноту связи и постройте линейное
уравнение взаимосвязи
Стоимость основных
производственных фондов,
млн.руб. x
Объем валовой продукции,
млн.руб. y
1
2
3
4
5
20
25
31
31
40
6
7
8
56
52
60
9
60
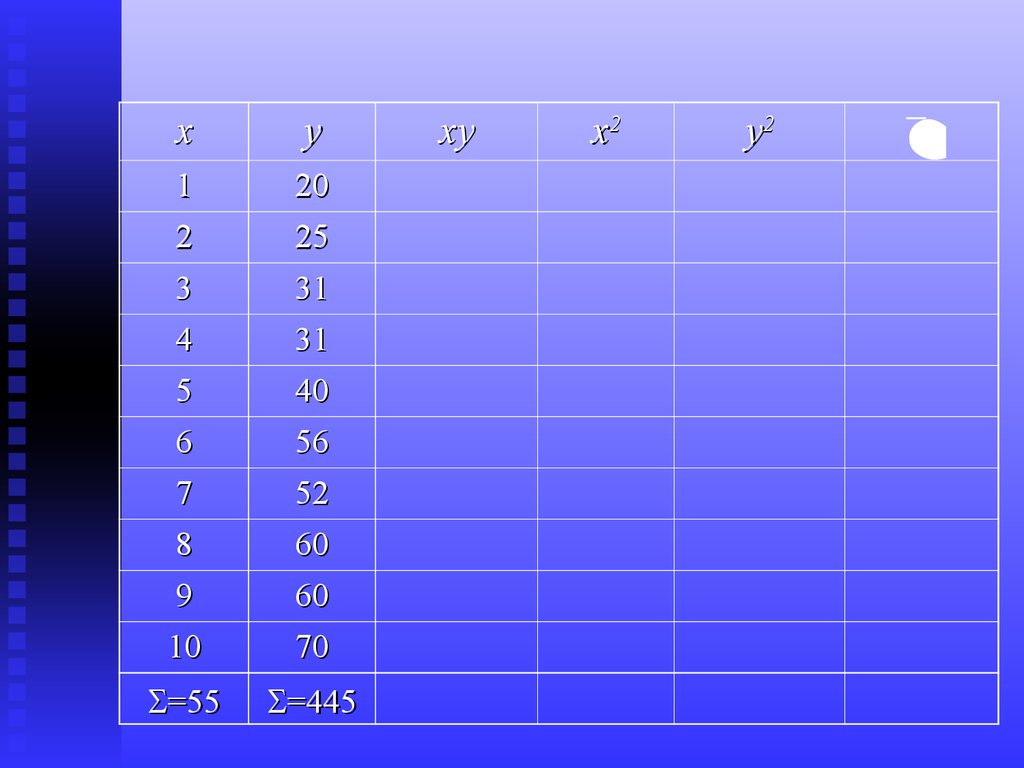
15.
xy
1
2
20
25
3
4
5
6
31
31
40
56
7
8
9
52
60
60
10
70
=55
=445
xy
x2
y2
yx
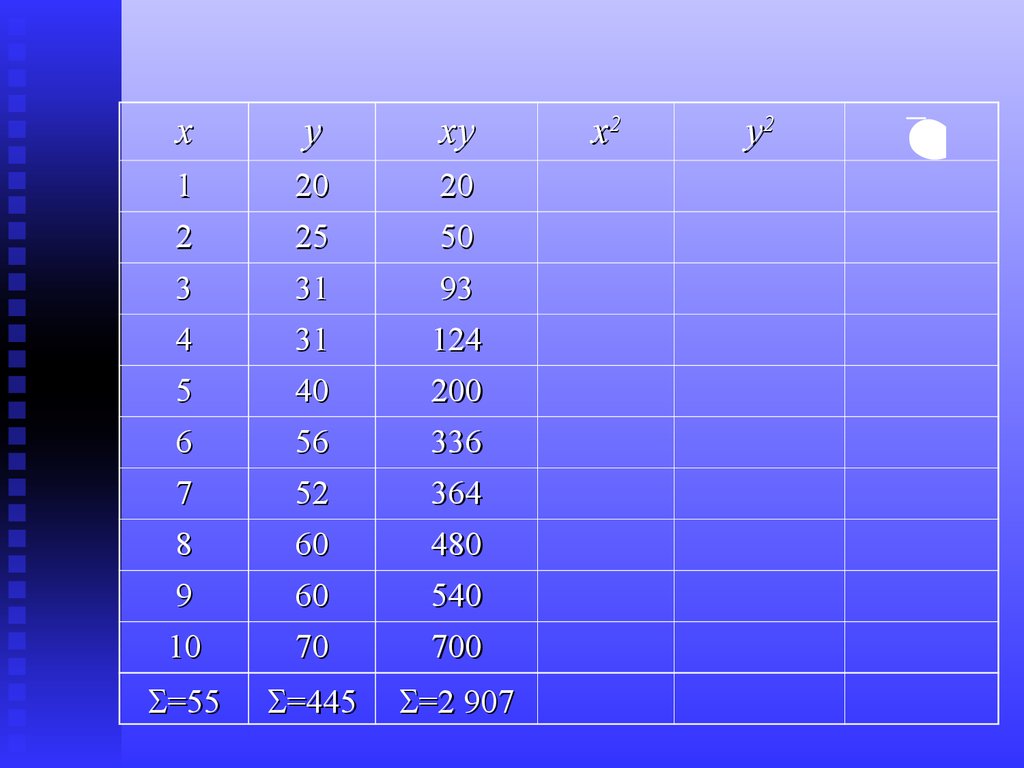
16.
xy
xy
1
2
20
25
20
50
3
4
5
6
31
31
40
56
93
124
200
336
7
8
9
52
60
60
364
480
540
10
70
700
=55
=445
=2 907
x2
y2
yx
17.
xy
xy
x2
1
2
20
25
20
50
1
4
3
4
5
6
31
31
40
56
93
124
200
336
9
16
25
36
7
8
9
52
60
60
364
480
540
49
64
81
10
70
700
100
=55
=445
=2 907
=385
y2
yx
18.
xy
xy
x2
y2
1
2
20
25
20
50
1
4
400
625
3
4
5
6
31
31
40
56
93
124
200
336
9
16
25
36
961
961
1 600
3 136
7
8
9
52
60
60
364
480
540
49
64
81
2 704
3 600
3 600
10
70
700
100
4 900
=55
=445
=2 907
=385
=22 487
yx
19. Решение:
a 11053 3,6,858a516 x429507
y5a1x010
Решение:
20.
yxx
y
xy
x2
y2
1
2
20
25
20
50
1
4
400
625
19,4
25,0
3
4
5
6
31
31
40
56
93
124
200
336
9
16
25
36
961
961
1 600
3 136
30,6
36,2
41,8
47,4
7
8
9
52
60
60
364
480
540
49
64
81
2 704
3 600
3 600
53,0
58,6
64,2
10
70
700
100
4 900
69,8
=55
=445
=2 907
=385
=22 487
=446
21.
r0
,
9
8
x
y
2
9
0
7
x
y
2
9
0
,
7
1
4
5
5
y
4
,
5
x
,yxr1xy0
5
1
0
2
, 23901,6753 7
2
4
8
,85,2 427,
4
,52 08,79838
1
6
22. Парная нелинейная зависимость
a1
y
x
0
x
1
na0
a01
y
1
x
1
y
a
1
2
xxx
Парная нелинейная зависимость
23. Корреляционное отношение
01
1
ост yn
2осyт
2
2ix
Корреляционное отношение
24. Ранговый коэффициент корреляции Спирмена
6d
d
11
n
T
R
1
2
3
2
2
y
x
1
3
T 2ti i
Ранговый коэффициент
корреляции Спирмена
25. Ранговый коэффициент корреляции Спирмена
d1
R
1
2yx2
Ранговый коэффициент
корреляции Спирмена
1
6 d
2
n n
3
26.
,0,53 30,750
- очень слабая связь,
практически отсутствует
- связь слабая
- связь средняя
- связь тесная
27.
Стоимость основныхфондов, xi
Производство
продукции, yi
Rx
Ry
d2
6,8
5,4
3
1
4
9,0
10,9
5
7
4
8,0
6,8
4
3
1
9,9
8,5
6
4
4
6,5
9,3
2
5
9
10,2
9,8
7,5
6
2,25
5,4
6,5
1
2
1
12,0
15,6
9
9
0
10,2
12,9
7,5
8
0,25
14,5
16,4
10
10
0
=25,5
28.
13
T
2
3
1 03 150,3 0,84
6
29. Ранговый коэффициент корреляции Кенделла
2S
n2
Ранговый коэффициент
корреляции Кенделла
S
( n 2 n)
( n 2 n)
2 Vx 2 V y
30.
12
V
t2
xy
31. Алгоритм расчета рангового коэффициента корреляции Кенделла
1.2.
3.
Значения Х ранжируются в порядке
возрастания или убывания
Значения У располагаются в порядке
соответствующем значениям Х
Для каждого значения У определяется
количество рангов следующих за ним и
превышающих его величину. Сумма
данных значений обозначается - Р
32. Алгоритм расчета рангового коэффициента корреляции Кенделла
4. Для каждого значения У определяется5.
количество рангов следующих за ним и
меньших по величине. Сумма данных
значений обозначается – Q. И
фиксируется со знаком минус.
Определяется S=P+Q
33.
0,53 0,30,75
- очень слабая связь,
практически отсутствует
- связь слабая
- связь средняя
- связь тесная
34.
23
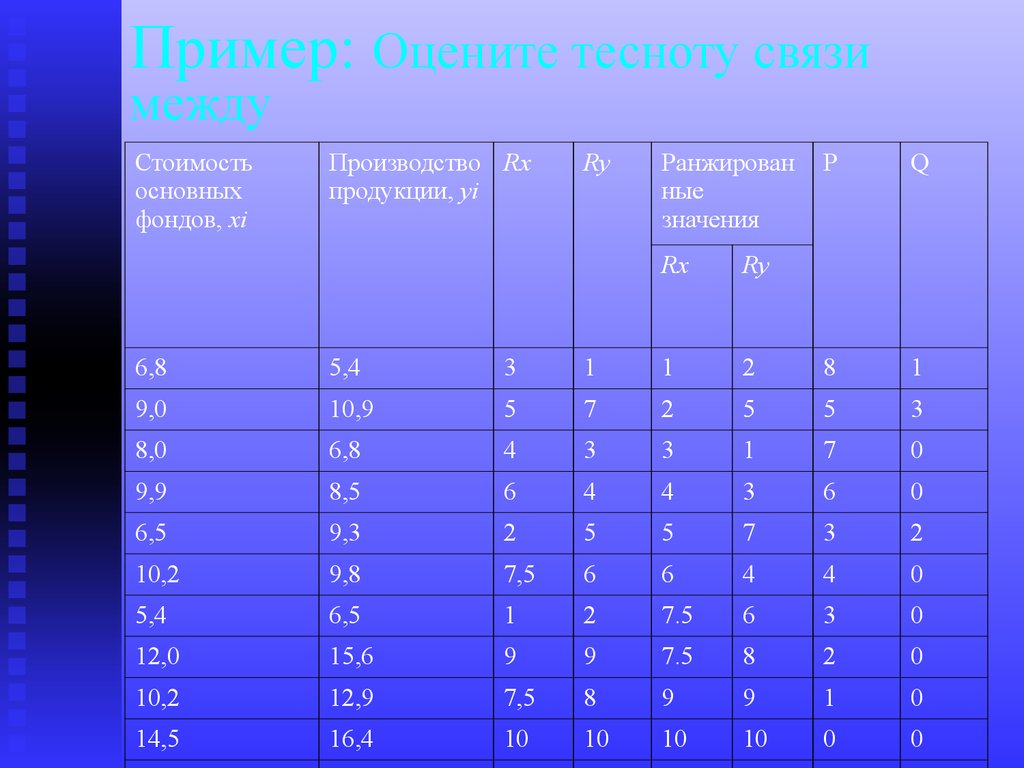
35. Пример: Оцените тесноту связи между
Стоимостьосновных
фондов, xi
Производство Rx
продукции, yi
Ry
Ранжирован
ные
значения
Rx
Ry
Р
Q
6,8
5,4
3
1
1
2
8
1
9,0
10,9
5
7
2
5
5
3
8,0
6,8
4
3
3
1
7
0
9,9
8,5
6
4
4
3
6
0
6,5
9,3
2
5
5
7
3
2
10,2
9,8
7,5
6
6
4
4
0
5,4
6,5
1
2
7.5
6
3
0
12,0
15,6
9
9
7.5
8
2
0
10,2
12,9
7,5
8
9
9
1
0
14,5
16,4
10
10
10
10
0
0
36.
12
V
2
2
1
x
3
(102 10)/2 1 (02 10)/2 0.74
S=39+(-6)=33
37. Ранговый коэффициент конкордации
12
S
W
m
2(
3
n )
Ранговый коэффициент
конкордации
38.
m – количество факторовn – число наблюдений
S – отклонение суммы квадратов рангов от
средней квадратов рангов
39. Оцените тесноту связи
Стоимость основныхфондов, xi
Производство
продукции,
yi
Численность
работаю
щих, zi
Rx
Ry
Rz
Сумма
стр
ок
Квадрат
ы
сумм
6,8
5,4
21
3
1
1
5
25
9,0
10,9
35
5
7
7
19
361
8,0
6,8
25
4
3
2
9
81
9,9
8,5
30
6
4
4
14
196
6,5
9,3
36
2
5
8
15
225
10,2
9,8
32
7
6
5
18
324
5,4
6,5
29
1
2
3
6
36
12,0
15,6
37
9
9
9
27
729
10,3
12,9
33
8
8
6
22
484
14,5
16,4
40
10
10
10
30
900
165
3361
40.
16
5
SW
33
61
3
6
,
1
0
2( 03 6,1) 0,45
2
23
41. Коэффициент знаков Фехнера
ab
К
ф
Коэффициент знаков Фехнера
где a – число совпадений знаков
отклонений значений признака от их
средней величины
b – число несовпадений знаков отклонений
значений признака от их средней величины
42.
1 К1ф
Кф со знаком “+” – связь прямая
Кф со знаком “-” – связь обратная
43.
,0,35 КК
0
3
ф
,К
0
5
ф
7
ф
0,
ф
- очень слабая связь,
практически отсутствует
- связь слабая
- связь средняя
- связь тесная
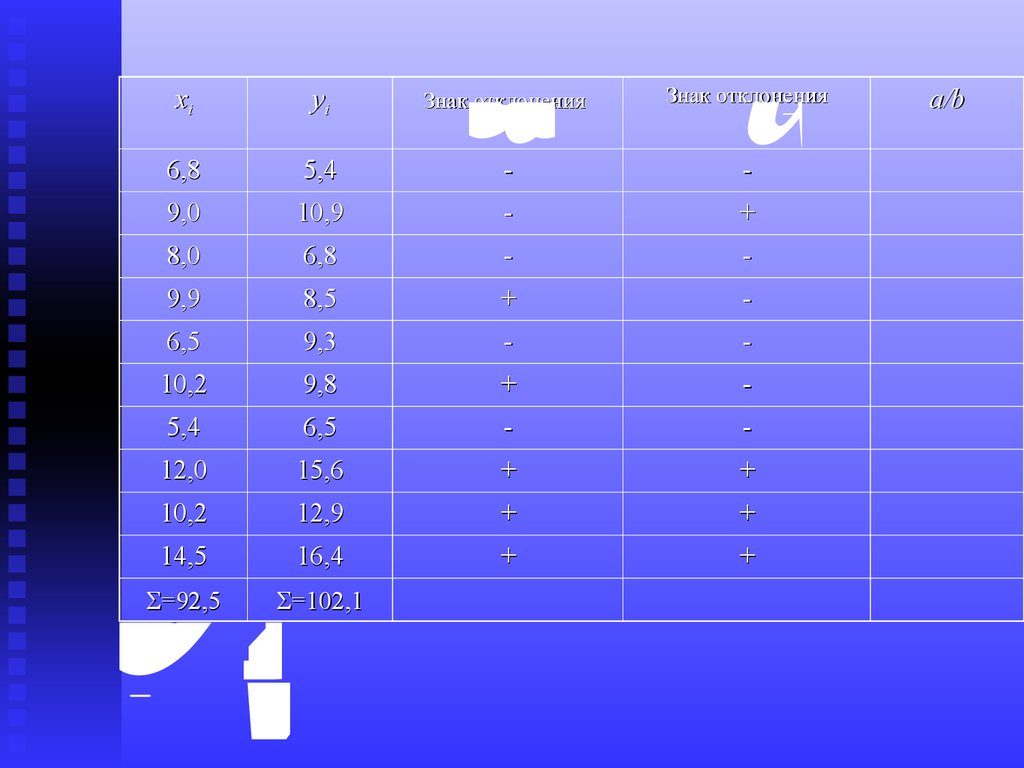
44. Пример: Оцените тесноту связи между
xiотyiотyПример: Оцените тесноту связи между
xi
yi
6,8
5,4
9,0
10,9
8,0
6,8
9,9
8,5
6,5
9,3
10,2
9,8
5,4
6,5
12,0
15,6
10,2
12,9
14,5
16,4
=92,5
=102,1
Знак отклонения
Знак отклонения
a/b
45.
xiотyiотyx 9,25
xi
yi
Знак отклонения
6,8
5,4
-
9,0
10,9
8,0
6,8
9,9
8,5
+
6,5
9,3
-
10,2
9,8
+
5,4
6,5
-
12,0
15,6
+
10,2
12,9
+
14,5
16,4
+
=92,5
=102,1
-
Знак отклонения
a/b
46.
xiотyiотyxy 190,25
xi
yi
Знак отклонения
Знак отклонения
6,8
5,4
-
-
9,0
10,9
-
+
8,0
6,8
-
-
9,9
8,5
+
-
6,5
9,3
-
-
10,2
9,8
+
-
5,4
6,5
-
-
12,0
15,6
+
+
10,2
12,9
+
+
14,5
16,4
+
+
=92,5
=102,1
a/b
47.
xiотyiотyy 10,2ф
x 9,25К
7
3
10 0,4
xi
yi
Знак отклонения
Знак отклонения
a/b
6,8
5,4
-
-
a
9,0
10,9
-
+
b
8,0
6,8
-
-
a
9,9
8,5
+
-
b
6,5
9,3
-
-
a
10,2
9,8
+
-
b
5,4
6,5
-
-
a
12,0
15,6
+
+
a
10,2
12,9
+
+
a
14,5
16,4
+
+
a
=92,5
=102,1
a=7
b=3
48. Оценка тесноты связи между качественными признаками
- коэффициент ассоциации- коэффициент контингенции
-коэффициент взаимной
сопряженности Пирсона
-коэффициент взаимной
сопряженности Чупрова
49. Коэффициент ассоциации
Ac
a
d
b
Коэффициент ассоциации
Где a,b,c,d - частоты внутри
таблицы сопряженности
50.
A 0,51 A1- связь существует
A со знаком “+” – связь прямая
A со знаком “-” – связь обратная
51. Коэффициент контингенции
1 K1a
d
b
c
K
K a0, 3b c d c d
Коэффициент контингенции
- связь существует
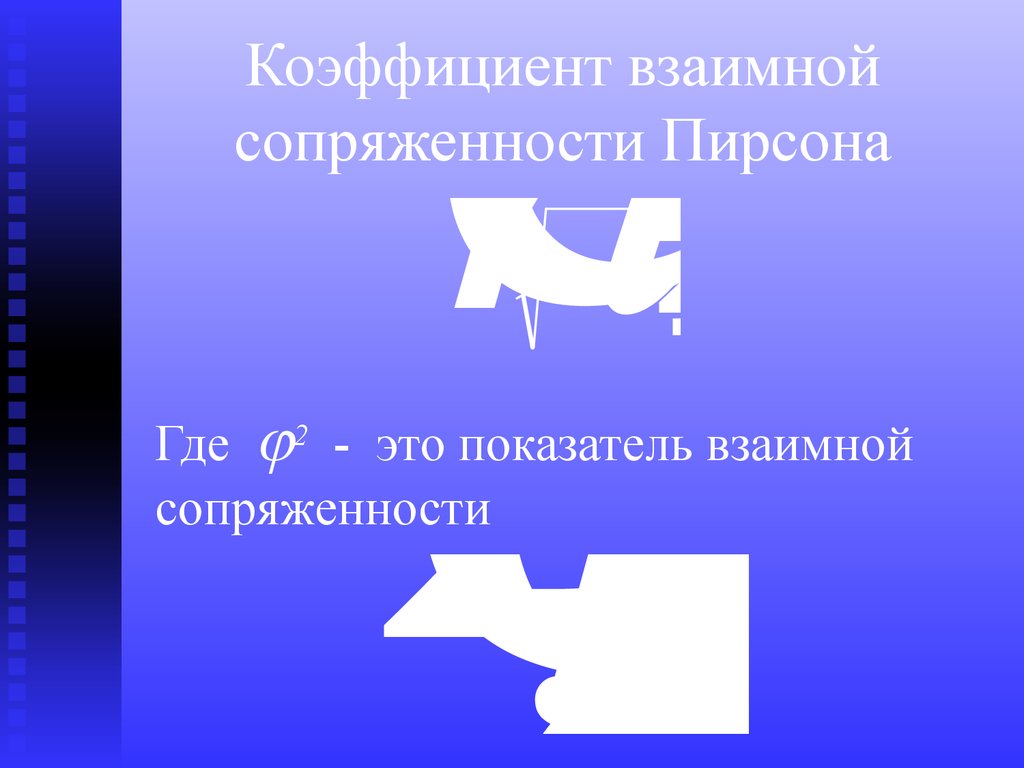
52. Коэффициент взаимной сопряженности Пирсона
c1
n
x
y
2
1
2
п
2
Коэффициент взаимной
сопряженности Пирсона
Где 2 - это показатель взаимной
сопряженности
53. Коэффициент взаимной сопряженности Чупрова
c к 1 к 12
ч12
Коэффициент взаимной
сопряженности Чупрова
54.
0c
1
c 10
- связь слабая
- связь тесная
55. Пример: определите тесноту связи между цветом глаз матерей и дочерей
Цвет глаздочерей
светлые
темные
Итого
Цвет глаз матерей
светлые
темные
471
151
622
148
230
378
Итого
619
381
1000
56.
A4
7
1
2
3
0
1
5
4
8
5
9
8
2
0
,
6
1
3
0
6
7
K
6973481 0,37
4
7
1
2
3
0
1
5
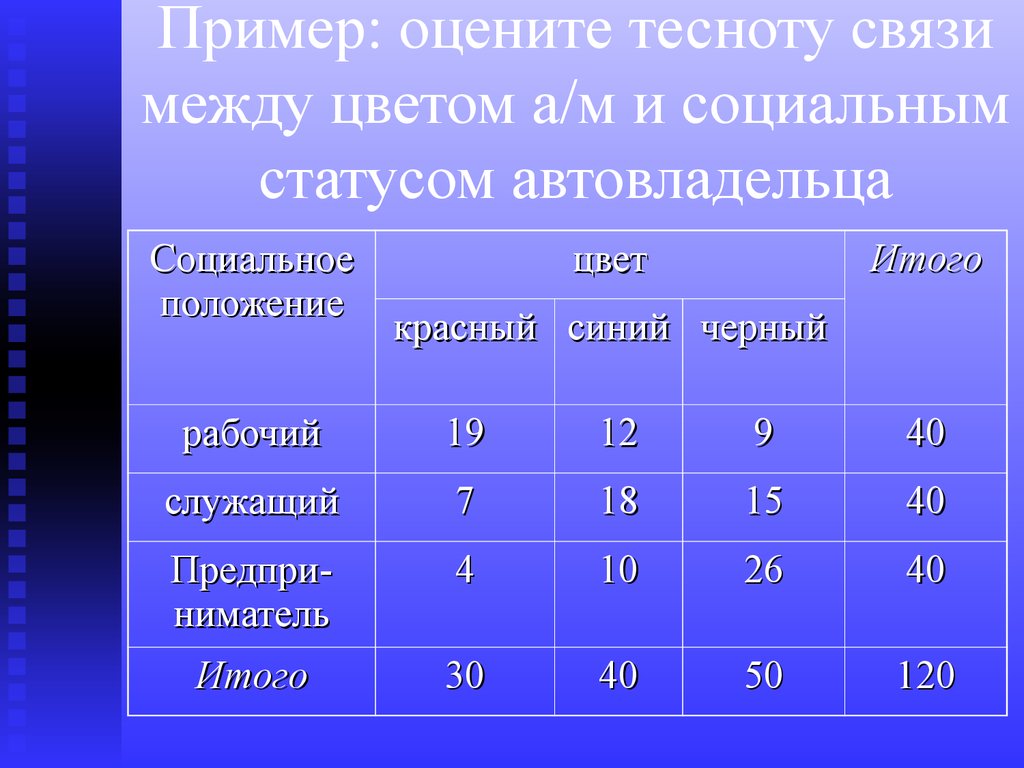
57. Пример: оцените тесноту связи между цветом а/м и социальным статусом автовладельца
Социальноеположение
цвет
Итого
красный синий черный
рабочий
19
12
9
40
служащий
7
18
15
40
Предприниматель
4
10
26
40
Итого
30
40
50
120
58.
22
2
2
1
9
1
2
9
7
2
83c
4
0
п5
4
0
1
4
0
5
4
0
3
2
1
2
6
1
0
,
2
4
3
5
0
,ч(3 )2 (34 )0,4132
0
59. Проверка значимости коэффициентов корреляции
60. Проверка значимости парного линейного коэффициента корреляции.
61. Например:
,rxy 1673 85,2 47,5 0,982
9
0
Например:























































 Математика
Математика Социология
Социология








