Похожие презентации:
1-е начало термодинамики. Адиабатический процесс
1. Лекция 14 (2 сем). 1-е начало термодинамики. Адиабатический процесс
Курс физики для студентов 1-2 курса БГТУКафедра физики БГТУ
доцент Крылов Андрей Борисович
Часть II.
ОСНОВНЫЕ ЗАКОНЫ
термодинамики и
молекулярной
физики
Лекция 14 (2 сем).
1-е начало термодинамики. Адиабатический
процесс
1. Количество теплоты и работа. 1-е начало термодинамики.
2. Теплоёмкость вещества. Виды теплоемкостей.
3. Применение I начала термодинамики к изопроцессам идеальных газов.
4. Адиабатический процесс. Уравнение Пуассона в трёх видах.
5. Политропные процессы.
2017
1
+3
2. 1. Количество теплоты и теплообмен
Теплообмен - процесс передачи внутренней энергии от одного тела кдругому без совершения работы (без изменения объема).
Количество теплоты Q – это количество энергии, передаваемое системе
внешними телами при теплообмене.
Сообщение системе теплоты Q не связано с макроскопическими перемещениями
тел системы.
Изменение внутренней энергии при теплообмене состоит в том, что
отдельные молекулы более нагретого тела в процессе неупругих столкновений
передают часть своей кинетической энергии молекулам менее нагретого
тела.
Существует три вида теплообмена: теплопроводность, конвекция, излучение.
Теплопроводность – это процесс теплообмена между телами при их
непосредственном контакте, обусловленный хаотическим движением частиц тела.
Конвекция - процесс переноса энергии, который осуществляется перемещением
слоев жидкости и газа от места с более высокой температурой к месту с более низкой
температурой. Конвекция наблюдается только в жидкостях и газах.
Излучение - перенос энергии от одного тела к другому (а также между частями
одного и того же тела) путем обмена электромагнитным излучением, т.е. теплообмен,
обусловленный процессами испускания, распространения, рассеяния и поглощения
электромагнитных волн.
Передача энергии излучением может осуществляться при отсутствии
материальной среды, разделяющей поверхности теплообмена, т.е. в полном
вакууме.
2
+7
3. Работа и внутренняя энергия
Внутреннюю энергию можно также изменить путем совершения работы.Передача внешними телами энергии в форме работы сопровождается
макроскопическими перемещениями внешних тел.
Например:
1. Если внешняя сила вызывает деформацию тела, то при этом
изменяются расстояния между частицами, из которых оно состоит, а
следовательно, изменяется потенциальная энергия взаимодействия
частиц.
2.
Внутренняя энергия тела изменяется также при его неупругом
соударении с другим телом.
3.
При неупругих деформациях, кроме того, изменяется температура тела, то есть
изменяется кинетическая энергия теплового движения частиц.
Но при деформации тела совершается работа, которая и является мерой
изменения внутренней энергии тела.
При неупругом соударении тел их кинетическая энергия уменьшается, она
превращается во внутреннюю.
Мерой изменения кинетической энергии тела, согласно теореме о
кинетической энергии, является работа действующих сил.
Изменение внутренней энергии тела происходит под действием силы
трения, поскольку, как известно из опыта, трение всегда сопровождается
изменением температуры трущихся тел.
Работа силы трения может служить мерой изменения внутренней энергии.
3
+5
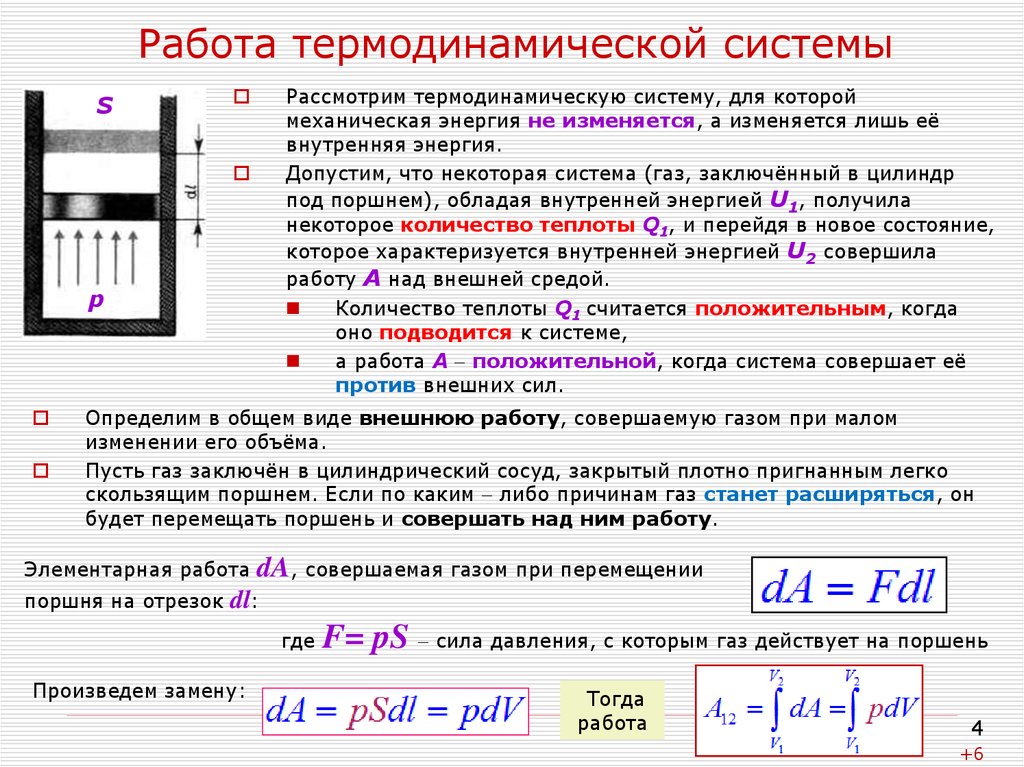
4. Работа термодинамической системы
SРассмотрим термодинамическую систему, для которой
механическая энергия не изменяется, а изменяется лишь её
внутренняя энергия.
Допустим, что некоторая система (газ, заключённый в цилиндр
под поршнем), обладая внутренней энергией U1, получила
некоторое количество теплоты Q1, и перейдя в новое состояние,
которое характеризуется внутренней энергией U2 совершила
работу А над внешней средой.
Количество теплоты Q1 считается положительным, когда
оно подводится к системе,
а работа А положительной, когда система совершает её
против внешних сил.
p
Определим в общем виде внешнюю работу, совершаемую газом при малом
изменении его объёма.
Пусть газ заключён в цилиндрический сосуд, закрытый плотно пригнанным легко
скользящим поршнем. Если по каким либо причинам газ станет расширяться, он
будет перемещать поршень и совершать над ним работу.
Элементарная работа
поршня на отрезок
dA, совершаемая газом при перемещении
dl:
где
Произведем замену:
F= pS сила давления, с которым газ действует на поршень
Тогда
работа
4
+6
5. Первое начало термодинамики
Выражение справедливо при любых изменениях объёматвёрдых, жидких и газообразных тел.
В соответствии с законом сохранения энергии при любом способе перехода
системы из одного состояния в другое изменение внутренней энергии ΔU будет
одинаковым.
Это изменение будет равно разности между количеством теплоты Q, полученной
системой, и работой А, совершенной системой против внешних сил:
Первое начало термодинамики: теплота
изменение её внутренней энергии ΔU и на совершение ею работы А против
внешних сил.
В дифференциальной форме первое начало термодинамики имеет вид:
Q, сообщаемая системе, расходуется на
Если система периодически возвращается в первоначальное состояние, то изменение её
внутренней энергии равно нулю (ΔU=0).
Тогда согласно первому началу термодинамики А=Q, т.е. невозможен вечный
двигатель первого рода периодически действующий двигатель, который совершал
бы бóльшую работу, чем сообщённая ему извне энергия.
5
+5
6. 2. Теплоемкость. Виды теплоемкостей
Теплоёмкость тела - величина, равная количеству теплоты Q, которое нужносообщить телу, чтобы повысить его температуру на один Кельвин.
Если при сообщении телу количества теплоты dQ, его температура повышается на
dT, то его теплоемкость равна:
Единица измерения теплоёмкости в СИ: [Дж/К]
Из определения следует, что теплоемкость тела будет зависеть от химического
состава, массы, температуры, а также от вида процесса, определяющего изменение
состояния тела при сообщении ему теплоты dQ.
Теплоёмкость моля вещества = молярная теплоёмкость величина, равная
количеству теплоты, необходимому для нагревания одного моль вещества на один
Кельвин:
[Дж/(моль К)]
Удельная теплоёмкость – это теплоёмкость единицы массы вещества величина,
равная количеству теплоты, необходимому для нагревания одного килограмма
вещества на один Кельвин:
[Дж/(кг К)]
Получим связь между молярной и удельной теплоёмкостями одного и того же вещества:
где
М молярная масса вещества
6
+6
7. Теплоемкости при постоянных V и р
Величина теплоёмкости зависит от условий, при которых происходит нагреваниетела.
Если нагревание происходит при постоянном объёме (V=const – изохорный
процесс), то теплоёмкость называется теплоёмкостью при постоянном объёме
и обозначается:
и
Удельная теплоёмкость при
постоянном объёме
Молярная теплоёмкость при
постоянном объёме
Если нагревание происходит при постоянном давлении (р=const – изохорный
процесс), то теплоёмкость называется теплоёмкостью при постоянном
давлении и обозначается:
и
Молярная теплоёмкость при
постоянном давлении
Удельная теплоёмкость при
постоянном давлении
7
+5
8. 3. Применение 1-го начала термодинамики в изопроцессах
1. Изохорический процессИзопроцесс
Если газ нагревается или охлаждается при постоянном
объёме, то dV=0 и работа внешних сил равна нулю:
Сообщаемая газу извне теплота
внутренней энергии
Q пойдёт только на увеличение его
U:
Но
Молярная теплоёмкость при
постоянном объёме
Изменение внутренней энергии газа:
8
+7
9. Теплоемкости при изохорическом процессе
ИзопроцессЕсли
(для идеального газа справедливо)
Получим выражения для молярной и удельной теплоемкостей идеального газа
при постоянном объеме.
Вспомним, что для идеального газа изменение внутренней
энергии зависит от количества степеней свободы i:
Тогда молярная теплоёмкость при постоянном
объёме
Удельная теплоёмкость при постоянном объёме
9
+5
10. Применение 1-го начала термодинамики в изопроцессах
2. Изобарический процессИзопроцесс
Работа при постоянном давлении:
1-е начало термодинамики в данном случае:
Молярная теплоёмкость при
постоянном давлении
Продифференцируем при p=const:
уравнение состояния идеального газа или
уравнение Менделеева – Клапейрона.
10
+9
11. Применение 1-го начала термодинамики в изопроцессах
3. Изотермический процессИзопроцесс
Работа равна:
из уравнения МенделееваКлапейрона
Работа при постоянной температуре:
где
из уравнения БойляМариотта
Тогда
1-е начало термодинамики в данном случае:
где
так как температура не изменялась
11
+10
12. Теплоемкости при изобарическом процессе
ИзопроцессПолучим выражения для молярной и удельной теплоемкостей
идеального газа при постоянном давлении.
Удельная теплоёмкость при постоянном
давлении:
Тогда молярная теплоёмкость при постоянном давлении
Вывод: Молярная теплоемкость Cp газа в процессе с
постоянным
давлением
всегда
больше
молярной
теплоемкости CV в процессе с постоянным объемом
Мы получили формулу
Майера для молярных
теплоемкостей
12
+7
13. Подитожим формулы для изопроцессов
1314. 4. Адиабатический процесс
Адиабатический процесс - процесс , протекающий без теплообмена сокружающей средой. Подведённое к телу количество теплоты:
Q=0 или
δQ=0.
Определим уравнение состояния - уравнение, связывающее параметры
идеального газа при адиабатическом процессе.
Первое начало термодинамики можно записать в следующем виде:
где
Вывод: Работа газа при адиабатическом процессе происходит за счет
убыли внутренней энергии.
Учтем, что:
давление из уравнения
Менделеева-Клапейрона
Разделим переменные T и V:
Возьмем
определенный
интеграл:
14
+10
15. 4. Адиабатический процесс -2
формулаМайера
Зная формулу Майера, преобразуем
отношение:
где
γ - адиабатическая постоянная
Тогда
Избавимся от логарифмов – то,
что перед логарифмом есть
показатель степени логарифма:
Один из видов записи
уравнения Пуассона
15
+8
16. 2. Уравнение Пуассона – формула адиабатического процесса
Перейдём от этого уравнения к уравнению в переменных p,VИз уравнения Менделеева-Клапейрона температура Т:
где в знаменателе константы
Тогда
Основной вид записи уравнения Пуассона
Перейдём от этого уравнения к уравнению в переменных p,Т
Из уравнения Менделеева-Клапейрона объем V:
Третий из видов записи
уравнения Пуассона
16
+9
17. Работа газа при адиабатическом процессе
Адиабатический процесс - процесс , протекающий без теплообмена с окружающейсредой. Подведённое к телу количество теплоты:
Q=0 или δQ=0:
Учтем, что:
Возьмем
определенный
интеграл:
где
Учтем, что:
Из уравнения МенделееваКлапейрона температура Т1:
17
+11
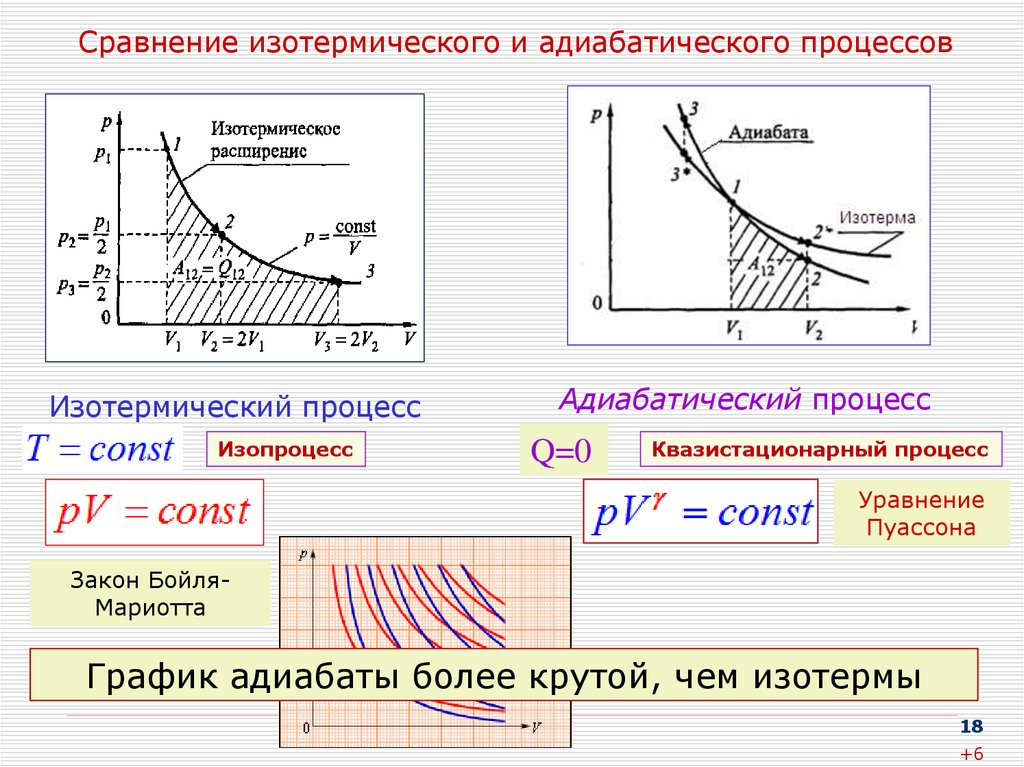
18. Сравнение изотермического и адиабатического процессов
Изотермический процессИзопроцесс
Адиабатический процесс
Q=0
Квазистационарный процесс
Уравнение
Пуассона
Закон БойляМариотта
График адиабаты более крутой, чем изотермы
18
+6
19. Подитожим для всех процессов
1920. 3. Политропические (политропные) процессы
Рассмотренные изохорный, изобарный, изотермический и адиабатическийпроцессы происходят при постоянной теплоёмкости.
Политропический процесс - процесс, при котором теплоёмкость тела
остаётся постоянной:
С=const.
Уравнение политропы для
идеального газа:
где
Показатель политропы
n = γ уравнение переходит в уравнение адиабаты:
При
При
n = 0 (СМ = СpМ) – в уравнение изобары:
При
n = 1 (СМ = ) – в уравнение изотермы:
При
n = (СМ = СVМ) – в уравнение изохоры:
20
+7
21. Работа при политропическом (политропном) процессе
Выразим давление p через объем V:где p и V – давление и объем в
любом промежуточном
состоянии
p1, V1 и p2, V2 – значения давления и объема газа соответственно в начальном и
конечном состояниях
Отсюда
Тогда работа:
Для случая, когда n 1, интеграл равен:
Для адиабаты
По закону МенделееваКлапейрона:
Для политропы
21
+9
22. Объяснение зависимости молярной теплоемкости от температуры на основе квантовых представлений
Согласно классической теореме о равнораспределении средняя энергия любого движениямолекулы при температуре равна:
где
i – число степеней свободы.
Однако, эта теорема выводится в предположении, что возможны любые значения энергии
движения, а в квантовой механике показывается, что энергия — квантованная величина.
Когда расстояние между энергетическими уровнями много меньше, чем тепловая
энергия — kT/2 на степень свободы, то разница между действительным дискретным
спектром и непрерывным пренебрежимо мала и закон о равнораспределении фактически
выполняется.
В противном случае происходит "вымораживание" степеней свободы, т. е. молекулы
собираются на нижнем энергетическом уровне для данного вида движения и
практически не покидают его, т. к. тепловой энергии соударений для этого не хватает.
Из-за этого теплоемкость реальных газов отличается от даваемой классической МКТ.
Например, водород представляет собой двухатомный газ, молекула которого имеет три
поступательные степени свободы, две вращательные и одну колебательную, поэтому его
теплоемкость по теореме о равнораспределении должна быть равна:
Но энергия колебаний молекулы водорода велика, поэтому при комнатной температуре молекулы
находятся в подавляющем большинстве на нижнем колебательном уровне, и колебательная степень
свободы оказывается "вымороженной".
Из-за этого теплоемкость водорода при комнатной температуре близка к 5R/2, и лишь при
температурах свыше 5000 К все степени свободы эффективно возбуждены и теплоемкость
подходит к теоретической 7R/2.
При понижении температуры до 80 К вымораживаются и вращательные степени свободы, и
теплоемкость водорода падает до 3R/2.
Аналогичные явления наблюдаются также в жидкостях и твердых телах.
22
+8
23. Спасибо за внимание!
Курс физики для студентов 1 курса БГТУКафедра физики БГТУ
доцент Крылов Андрей Борисович
Часть II.
ОСНОВНЫЕ ЗАКОНЫ
термодинамики и
молекулярной
физики
Спасибо за внимание!
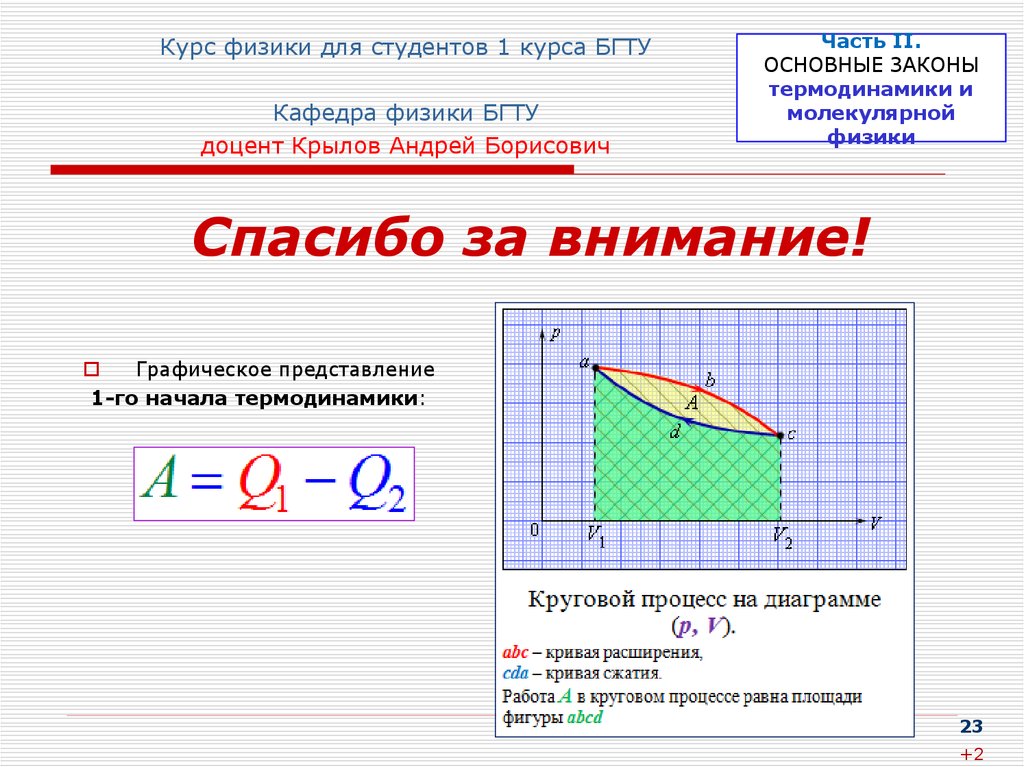
Графическое представление
1-го начала термодинамики:
23
+2




















 Физика
Физика