Первое начало термодинамики

1.

2.

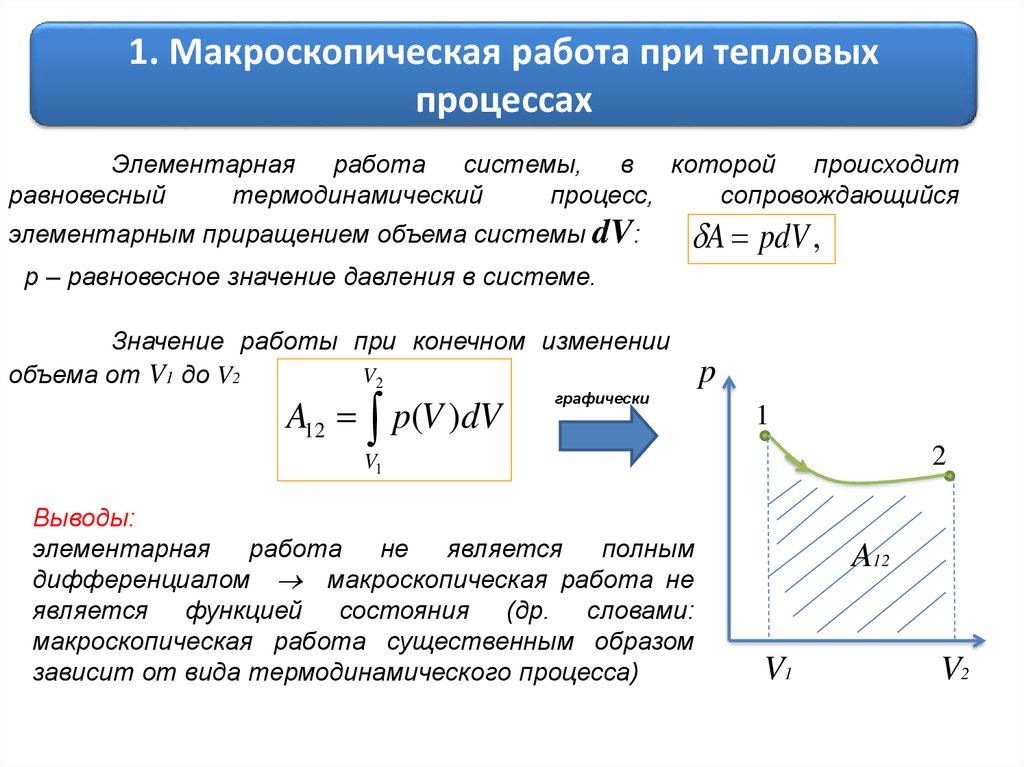
1. Макроскопическая работа при тепловых
процессах
Элементарная работа системы, в которой происходит
равновесный
термодинамический
процесс,
сопровождающийся
элементарным приращением объема системы dV:
A pdV ,
р – равновесное значение давления в системе.
Значение работы при конечном изменении
V2
объема от V1 до V2
A12 p(V )dV
графически
p
1
2
V1
Выводы:
элементарная работа не является полным
дифференциалом макроскопическая работа не
является функцией состояния (др. словами:
макроскопическая работа существенным образом
зависит от вида термодинамического процесса)
A12
V1
V2

3.

НАЗВАНИЕ ТД ПРОЦЕССА
1. Изобарный (р=const)
2. Изохорный (V=const)
ВЫРАЖЕНИЕ ДЛЯ РАБОТЫ
V2
V2
V1
V1
Ap pdV p dV p(V2 V1 ) p V
V2
AV pdV 0, т.к. dV 0
V1
3. Изотермический
(Т=const)
RT
AT p (V )dV p (V )
V
V
V2
1
V2
dV
V
RT ln 2
V
V1
V1
RT
4. Циклический (круговой)
процесс
Ao pdV A1I 2 A2 II1 0
p
II
1
Aо
2
I
V1
V2
V

4. 2. Внутренняя энергия идеального газа

Определение:
внутренняя
энергия идеального газа определяется как суммарная
энергия движения всех молекул
U N
i
kT
2
Выводы:
-1) внутренняя энергия является функцией состояния, т.е. ее
изменение не зависит от вида ТД процесса, а определяется только
изменением температуры конечного и начального состояния!
-2) изменение внутренней энергии равно нулю для кругового процесса и
изотермического
i
U RT
2
i
U R T
2
i
U pV
2
i
U p2V2 p1V1
2

5. 3. Количество теплоты. Первое начало термодинамики

Определения:
- теплообмен - обмен внутренними энергиями различных тел без
совершения макроскопической работы
- энергия, полученная какой-либо частью системы в результате
теплообмена называется количеством теплоты Q
1 постулат термодинамики (первое начало)
Q U A
в дифференциальной форме
Q dU A
Вывод: количество теплоты так же как и работа не является
функцией состояния!

6.

НАЗВАНИЕ ТД
ПРОЦЕССА
I – Е НАЧАЛО ТЕРМОДИНАМИКИ
1. Изобарный (р=const)
i
Q p U Ap R T p V p V R T
2
i
i 2
R T R T
R T
2
2
2. Изохорный (V=const)
i
QV U R T
2
3. Изотермический
(Т=const)
V2
QT AT RT ln
V1
4. Циклический
(круговой) процесс
Q0 A0
5. Адиабатический
(Q=0)
i
AQ U R T
2

7.

НАЗВАНИЕ ТД
ПРОЦЕССА
I – Е НАЧАЛО ТЕРМОДИНАМИКИ (в диф. форме)
1. Изобарный (р=const)
i
i 2
Q p dU A RdT pdV
RdT
2
2
2. Изохорный (V=const)
i
QV dU RdT
2
3. Изотермический
(Т=const)
QV A pdV
4. Адиабатический
(Q=0)
AQ dU

8. 4. Теплоемкость системы

Q
C0
dT
Определение:
- теплоемкостью некоторой системы называется
величина, численно равная количеству теплоты,
сообщенному
системе,
которое
вызывает
единичное приращение температуры этой системы
C0 c m C
c – удельная теплоемкость [Дж/кг∙К]
С – молярная теплоемкость [Дж/моль ∙ К]
c m
C
c
Вывод: теплоемкость системы
определяется видом ТД процесса
C
c
как
и
количество
теплоты

9.

НАЗВАНИЕ ТД ПРОЦЕССА
1. Изобарный (р=const)
2. Изохорный (V=const)
3. Изотермический
(Т=const)
4. Адиабатический (Q=0)
ВЫРАЖЕНИЯ ДЛЯ МОЛЯРНОЙ ТЕПЛОЕМКОСТИ
1 Qp i 2
R
Cp
2
dT
i
1 QV
R
2
dT
1 QV
CT
(т.к. dT 0)
dT
CV
CQ 0 (т.к. dQ 0)

10.

Вывод:
C p CV R
- уравнение Майера
Физический смысл R:
1 Q p QV 1 dU
V
R C p CV
p
dT
dT dT
T
dU Aм оль
dT
dT p
p
- универсальная газовая постоянная численно равна работе,
которую совершает один моль идеального газа при постоянном
давлении и при возрастании его температуры на один Кельвин
Cp
CV
i 2
i
5
1
3
показатель адиабаты

11.

5. Адиабатический процесс.
Уравнение Пуассона
Из 1-го начала ТД для адиабатического процесса имеем
A dU
1
1
RT
pV
1
1
1
dU
( pdV Vdp)
1
U
i 2
i
1
i
2 1
A pdV
1
A dU
( pdV Vdp) pdV
1
dp
dV
pdV Vdp
ln p ln V ln( const )
p
V
pV const
- уравнение Пуассона для адиабатического процесса

12.

Также используются выражения,
p
Критерий применимости
уравнений адиабаты:
Q=0
от
Из
скорость процесса должна удовлетворять
двум взаимоисключающим требованиям:
1) сохранению равновесности процесса
(процесс должен быть медленным);
2) процесс должен быть быстрым,
чтобы можно было пренебречь теплообменом
с окружающей средой
T2 >T1
иа
Ад
а
м
ер
T2 =const
ба
та
T1 =const
О
TV 1 const1 T p 1 const2
V
Выводы: газ охлаждается при адиабатическом расширении
и нагревается при адиабатическом сжатии.

13.

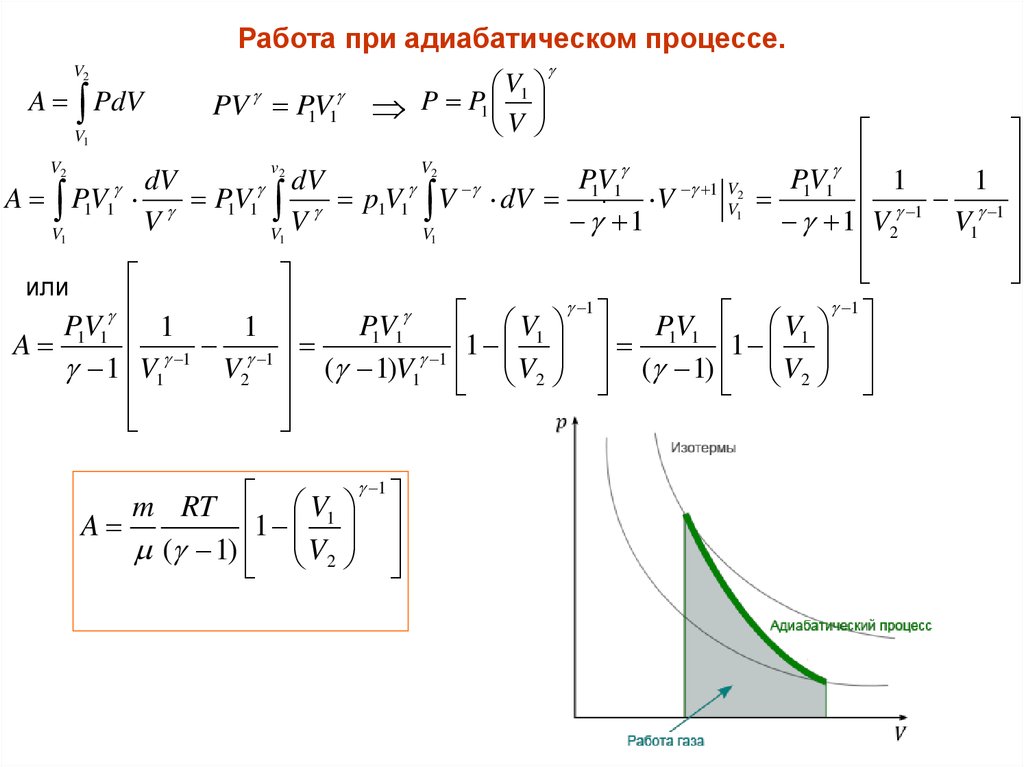
Работа при адиабатическом процессе.
V2
A PdV
PV P1V1
V1
V
P P1 1
V
2
2
P1V. 1
dV
dV
A P1V1 P1V1 p1V1 V dV
V 1
1
V
V
V1
V1
V1
V2
v
V
V2
V1
P1V1 1
1
1
1
1 V2
V1
1
1
P1V1 1
P1V1
V1
P1V1
V1
1
1
1
A
1
1
1
1 V1
V2
( 1)V1 V2 ( 1) V2
или
1
V1
m RT
1
A
( 1) V2