Информатика. Компьютерная графика

1. МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО

ОБРАЗОВАНИЯ
«МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(национальный исследовательский университет)»
(МАИ)
Кафедра эксплуатации и испытания летательных аппаратов
Информатика (2)
Компьютерная графика
Выполнил студент: Попов В.Д.
Группа: Т20-209с-16
Преподаватель: Козлова О.В.
Дата: 22.05.2018

2. Учебные вопросы:

1.
2.
3.
4.
5.
Растровые алгоритмы построения геометрических фигур
Отрезки прямой линии
Окружность и эллипс
Кривые и поверхности Безье
Методы обработки растровых изображений

3. Растровые алгоритмы построения геометрических фигур

4. Растровые алгоритмы построения геометрических фигур

Растровое изображение — это файл данных или структура,
представляющая собой сетку пикселей или точек цветов (на практике
прямоугольную) на компьютерном мониторе, бумаге и других
отображающих устройствах и материалах.

5. Растровые алгоритмы построения геометрических фигур

Важными характеристиками изображения являются:
- количество пикселей. Может указываться отдельно количество
пикселей по ширине и высоте (1024*768, 640*480,...) или же, редко,
общее количество пикселей (обычно измеряется в мегапикселях);
- количество используемых цветов (или глубина цвета);
- цветовое пространство RGB, CMYK, XYZ, YCbCr и др.

6. Отрезки прямой линии Алгоритм Брезенхема

7. Отрезки прямой линии

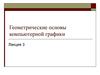
Алгоритм Брезенхэма— это алгоритм, определяющий, какие точки
двухмерного растра нужно закрасить, чтобы получить близкое
приближение прямой линии между двумя заданными точками.
Алгоритм широко используется, в частности, для рисования линий на
экране компьютера.

8. Отрезки прямой линии

Алгоритм
Отрезок рисуется между двумя точками — (x0,y0) и (x1,y1), где в этих
парах указаны колонка и строка, соответственно, номера которых
растут вправо и вниз. Сначала мы будем предполагать, что наша
линия идёт вниз и вправо, причём горизонтальное расстояние x1 − x0
превосходит вертикальное y1 − y0, т.е. наклон линии от горизонтали
— менее 45°. Наша цель состоит в том, чтобы для каждой колонки x
между x0 и x1, определить, какая строка y ближе всего к линии, и
нарисовать точку (x,y).

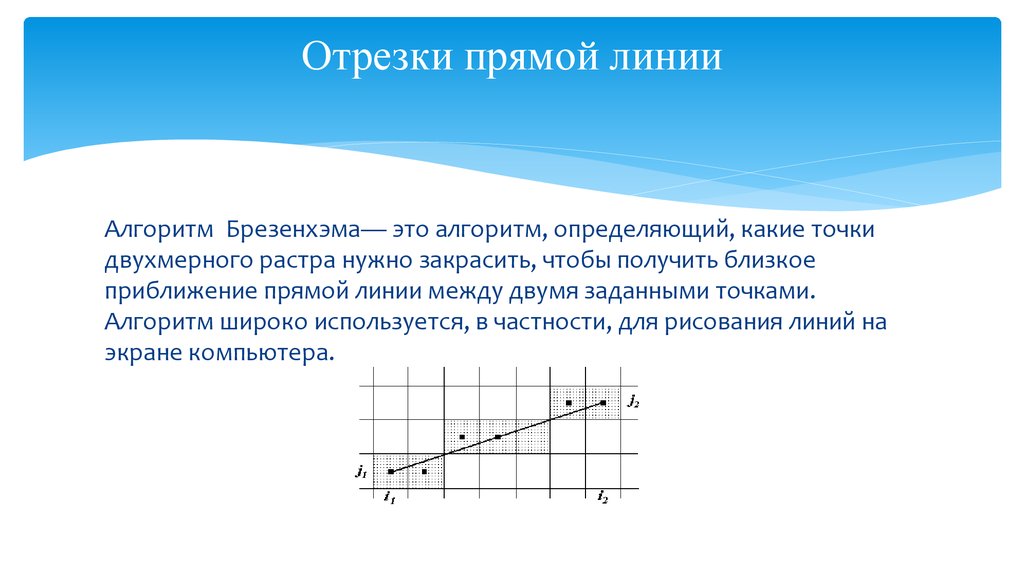
9. Отрезки прямой линии Иллюстрация работы алгоритма

10. Построение отрезка

Отрезки прямой линии
Построение отрезка
Общая формула линии между двумя точками:
Поскольку мы знаем колонку — x, то строка — y — получается
округлением к целому следующего значения:

11. Отрезки прямой линии

Однако, вычислять точное значение этого выражения — глупо;
достаточно заметить, что y растет от y0 и за каждый шаг мы
добавляем к x единичку и добавляем к y значение наклона которое
можно вычислить заранее. Более того, на каждом шаге мы делаем
одно из двух: либо сохраняем тот же y, либо увеличиваем его на 1.

12. Алгоритм построения окружности

13. Алгоритм построения окружности

Формулы, параметрически определяющие окружность.
Эти формулы достаточно просты и могут быть получены непосредственно из
определения тригонометрических функций. Согласно им окружность радиуса R с
центром в точке (x0, y0) может быть определена как множество точек M(x, y),
координаты которых удовлетворяют системе уравнений
x = x0 + R cos a
y = y0 + R sin a,
где a принадлежит [0;2p).

14. Алгоритм построения окружности

Но на самом деле мы строим не окружность, а правильный 360-угольник. Весьма
вероятно, что в недалеком будущем аппаратные средства позволят добиться
такой разрешающей способности дисплеев, что отличие многоугольника от
окружности станет заметным на глаз. Что мы станем делать тогда? Уменьшим шаг
приращения угла? Это неплохой выход, но такая ситуация обещает повториться.
Итак, приведенный алгоритм нас не устраивает. Надо поискать что-нибудь
свободное от упомянутых недостатков.

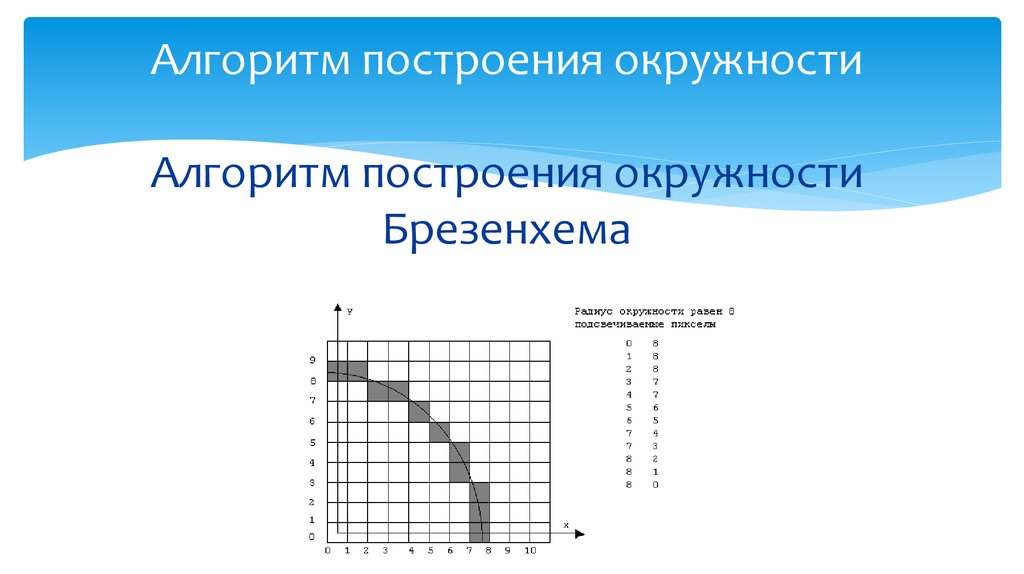
15. Алгоритм построения окружности Алгоритм построения окружности Брезенхема

16. Алгоритм построения окружности

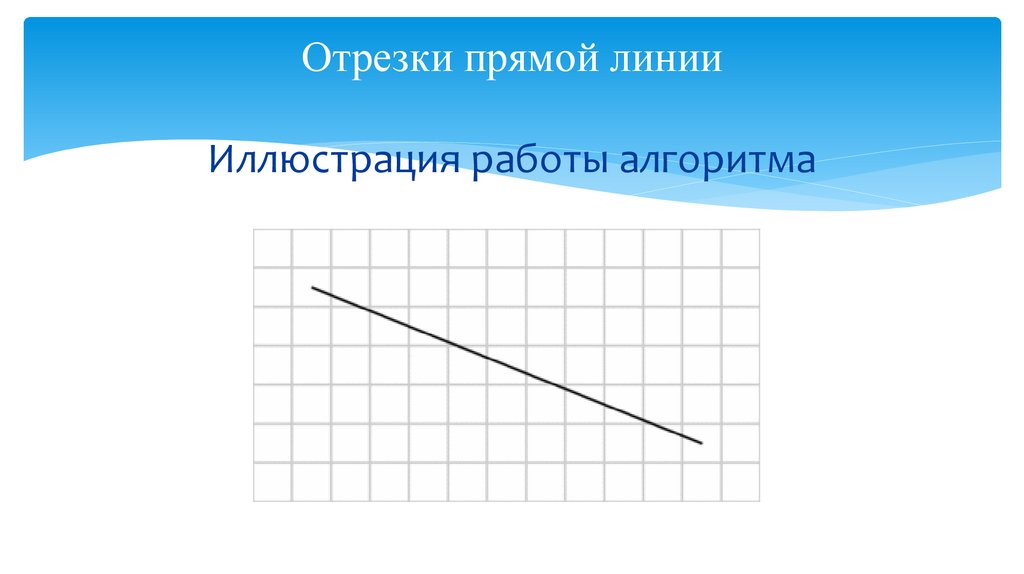
Окружность обладает центром симметрии и бесконечным
количеством осей симметрии. Поэтому нет необходимости строить
всю окружность, достаточно построить некоторую ее часть и
последовательным применением преобразований симметрии
получить из нее полную окружность. Мы станем строить 1/8 часть
окружности, заключенную в угле AOB.

17. Алгоритм построения окружности

Каждая точка этого фрагмента должна быть еще семь раз отображена с
помощью преобразований симметрии для получения полной
окружности.

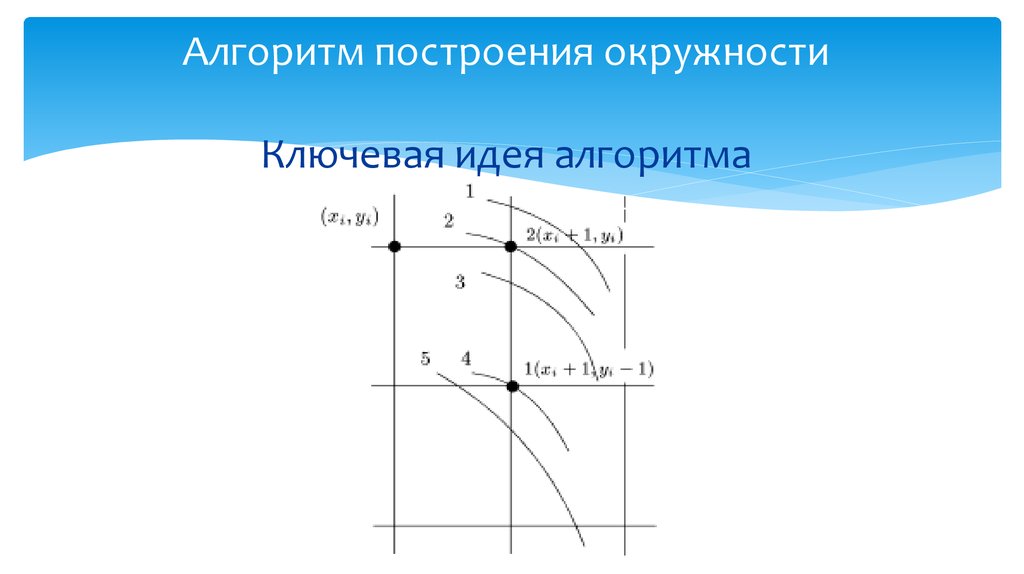
18. Алгоритм построения окружности Ключевая идея алгоритма

Пусть мы находимся в некоторой промежуточной фазе построения. Мы
только что поставили точку (xi, yi) и теперь должны сделать выбор
между точками 1(xi+1, yi-1) и 2(xi+1, y) .
Мы строим часть окружности, заключенную в угле AOB, следовательно,
подняться выше мы не можем и спуститься вниз более чем на одну
точку не можем тоже.

19. Алгоритм построения окружности Ключевая идея алгоритма

20. Алгоритм построения окружности Ключевая идея алгоритма

Реальная окружность может быть расположена
относительно точек 1 и 2 одним из пяти способов
1-5. Если мы выбераем точку 1, то тем самым
говорим, что (xi+1)2+(yi-1)2 » R2. Если же выбераем
точку 2, то допускаем, что (xi+1)2+(yi)2 » R2.
Рассмотрим две погрешности Di1 и Di2:
Di1 = (xi+1)2+(yi-1)2-R2
Di2 = (x1+1)2+(yi)2-R2
и контрольную величинуDi = Di1+Di2.

21. Алгоритм построения окружности Ключевая идея алгоритма

При выборе точки, следующей за (xi, yi), станем
руководствоваться следующим критерием:
если Di > 0, выберем точку 1;
если Di £ 0, выберем точку 2.
Обоснуем разумность такого выбора. Рассмотрим
знаки погрешностей Di1 и Di2 и их влияние на знак
контрольной величины Di для всех пяти возможных
положений окружности.

22. Алгоритм построения окружности

Простыми словами можно сказать что в этом алгоритме строится
дуга окружности для первого квадранта, а координаты точек
окружности для остальных квадрантов получаются симметрично. На
каждом шаге алгоритма рассматриваются три пикселя, и из них
выбирается наиболее подходящий путём сравнения расстояний от
центра до выбранного пикселя с радиусом окружности.

23. Кривые и поверхности Безье

Бикубические поверхности Кунса предоставляют гибкое и мощное
средство разработки поверхностей. Однако их практическое
использование, как и для кубических сплайновых кривых,
затрудняется необходимостью задания точной, интуитивно
неочевидной математической информации, например координат
точек, касательных векторов и векторов кручения.

24. Кривые и поверхности Безье

Возникающие проблемы иллюстрируются на рисунках. Большинство из этих
проблем можно преодолеть, распространив понятия кривых Безье на поверхности.

25. Кривые и поверхности Безье

Поверхность Безье параметрическая поверхность, используемая в компьютерной графике,
автоматизированном проектировании, и моделировании. Это одно из
распространённых пространственных обобщений кривой Безье.

26. Кривые и поверхности Безье

При кусочном моделировании для задания и изменения формы куска, представляю
щего
собой пространственную решетку из сплайнов или Многоугольников, применяется
сеть контрольных точек.
Эти точки управления, также известные как контрольные вершины оказывают на ги
бкую
поверхность куска подобное магнитному влияние, при котором поверхность растяг
ивается в том или ином
направлении. Кроме того, куски можно и дальше подразделять на элементы для до
стижения большего
разрешения и «сшивать» друг с другом, тем самым создавая сложные объёмные по
верхности. Так же, как исплайновые, кусочные модели используются при создании
органических форм.

27. Кривые и поверхности Безье

Декартово или тензорное произведение поверхности Безье задается
в виде

28. Методы обработки растровых изображений

В общем случае обработка
растровой графики сводится к
изменению цвета точек изображения
целиком или его отдельной области.
Даже простая операция
масштабирования растрового
документа требует определенных
расчетов, так как при увеличении
изображения увеличивается размер
растровой точки, что приводит к
ухудшению качества.

29. Методы обработки растровых изображений

Растровые изображения можно:
• кадрировать – вырезать необходимую часть изображения;
• коллажировать – соединять несколько изображений друг с другом, вносить детали одних изображений в
другие, добавлять текст и пр.;
• ретушировать – устранять дефекты изображения, изменять детали;
• трансформировать, деформировать (возможна потеря в качестве), отображать зеркально, разворачивать;
• изменять цвет, тон, контраст, насыщенность всего изображения или его частей;
• изменять посредством специальной обработки – фильтров, эффектов, наложения текстур, теней,
подсветки и пр.
Существует множество других вариантов, соответствующих возможностям графического редактора.

30. Методы обработки растровых изображений

Преимущества растровой графики
Растровый тип описания графики обладает следующими преимуществами:
• в растровом виде представимо любое изображение;
• растровая графика позволяет создать практически любой рисунок, вне зависимости
от сложности, в отличие, например, от векторной, где невозможно точно передать
эффект перехода от одного цвета к другому без потерь в размере файла;
• распространенность – растровая графика используется сейчас практически везде: от
маленьких значков до плакатов;
• высокая скорость обработки сложных изображений, если не нужно
масштабирование.
Растровое представление изображения естественно для большинства устройств
ввода-вывода графической информации, таких как мониторы (за исключением
векторных устройств вывода), матричные и струйные принтеры, цифровые
фотоаппараты, сканеры, а также сотовые телефоны.

31. Методы обработки растровых изображений

Недостатки растровой графики
Растровый вид представления графики имеет следующие недостатки:
• больший объем памяти, необходимый для работы с изображениями, высокая
требовательность к ресурсам компьютера;
• большие размеры файлов, зависимость размера файла от качества и размера
изображения;
• сложность обработки, потери при редактировании, невозможность идеального
масштабирования. В процессе преобразования растрового изображения
исходными данными является только описание набора пикселей, поэтому
возникает проблема замены меньшего числа пикселей на большее (при
увеличении) или большего на меньшее (при уменьшении);
• невозможность вывода на печать на векторный графопостроитель.
Из-за этих недостатков для хранения простых рисунков рекомендуют вместо даже
сжатой растровой графики использовать векторную графику.

32. Конец презентации

СПАСИБО ЗА ВНИМАНИЕ!