БКШ-сверхпроводимость. Терагерцовая оптика

1. БКШ-сверхпроводимость

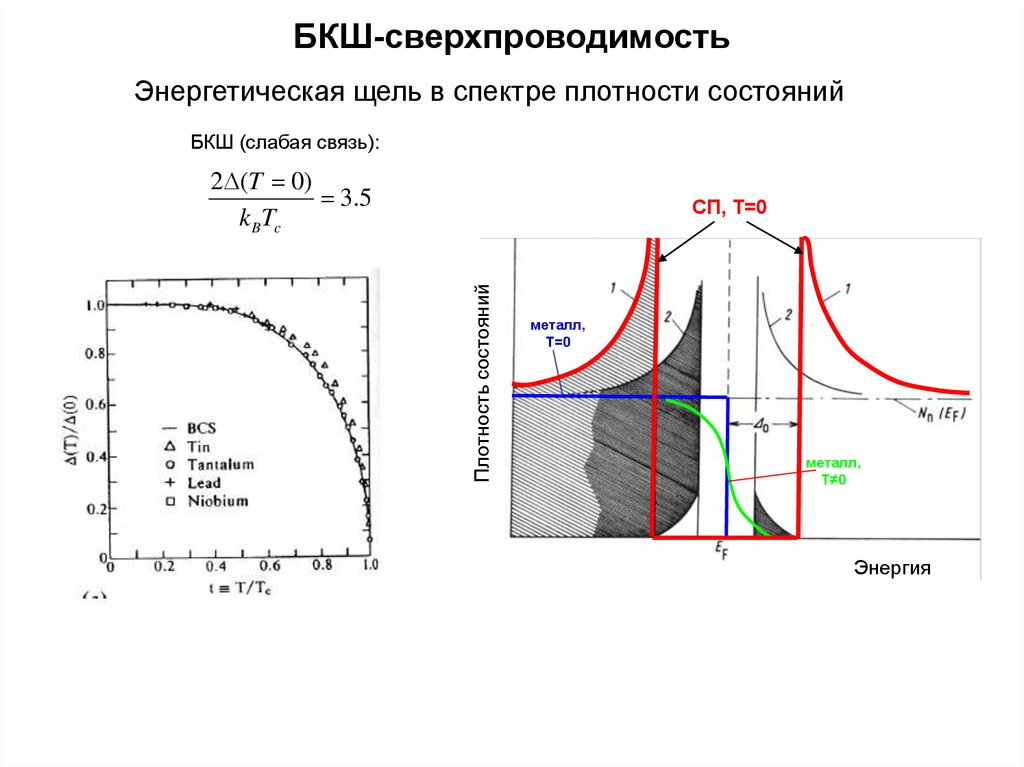
Энергетическая щель в спектре плотности состояний
БКШ (слабая связь):
2D (T 0)
3.5
k BTc
D/D0
Плотность состояний
СП, Т=0
металл,
T=0
металл,
T≠0
Энергия

2.

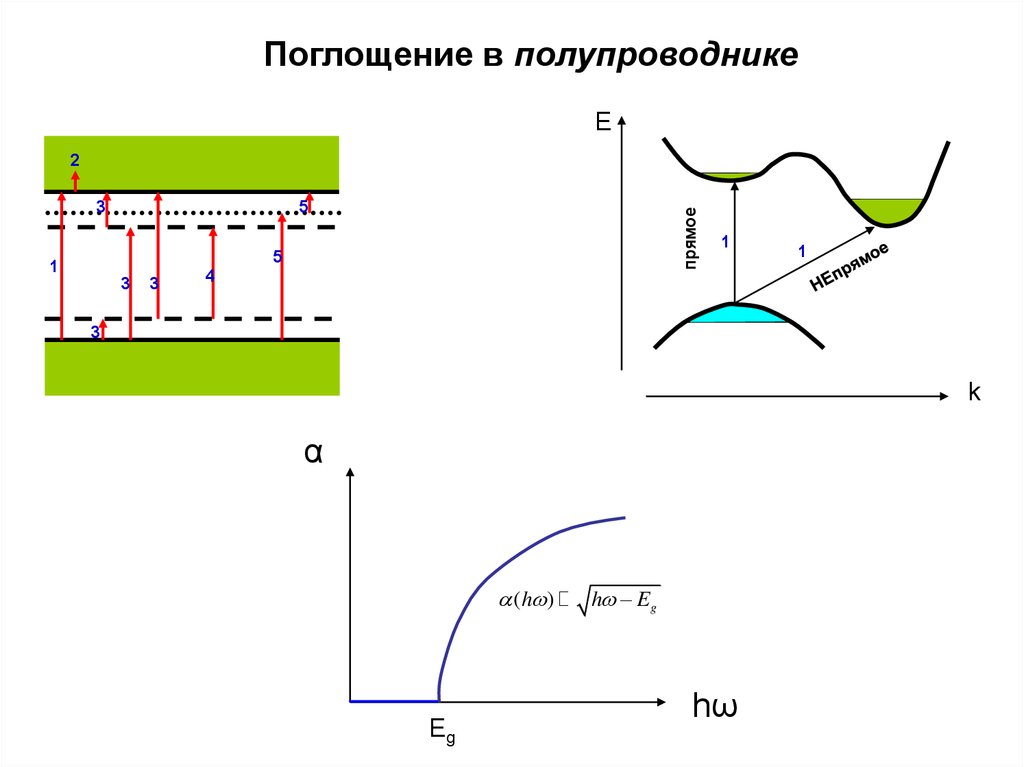
Поглощение в полупроводнике
E
2
5
прямое
3
5
1
3
3
4
1
1
3
k
α
(h )
Eg
h Eg
hω

3.

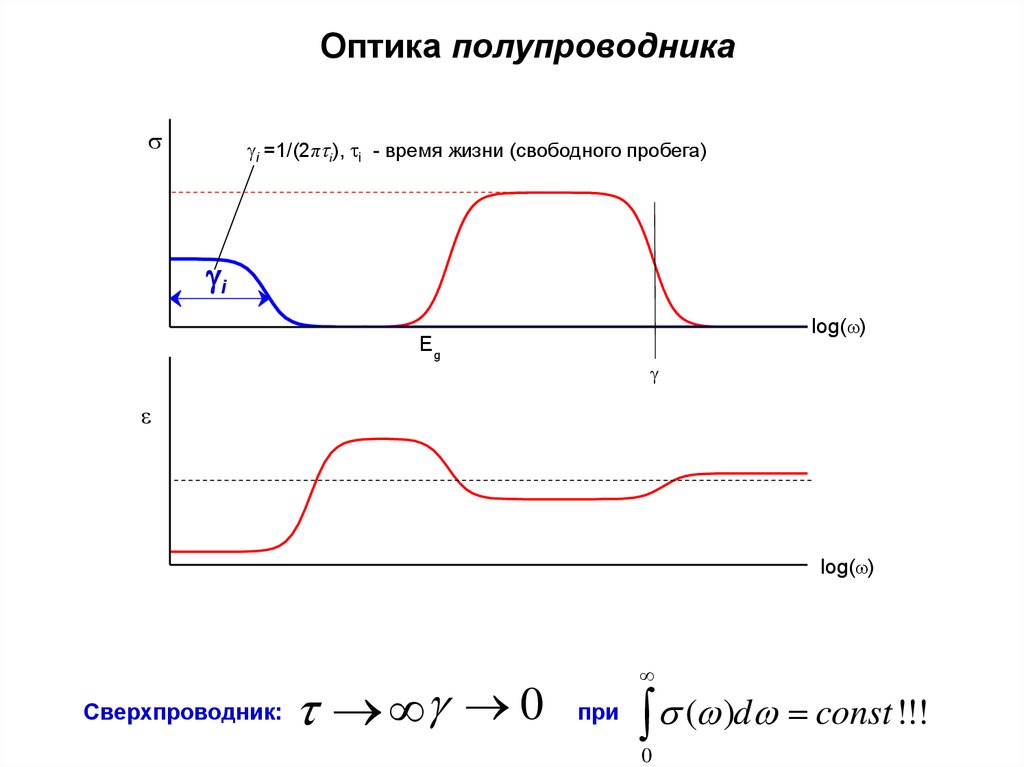
Оптика полупроводника
i =1/(2π i), i - время жизни (свободного пробега)
i
log( )
Eg
log( )
Сверхпроводник:
0
при
( )d const !!!
0

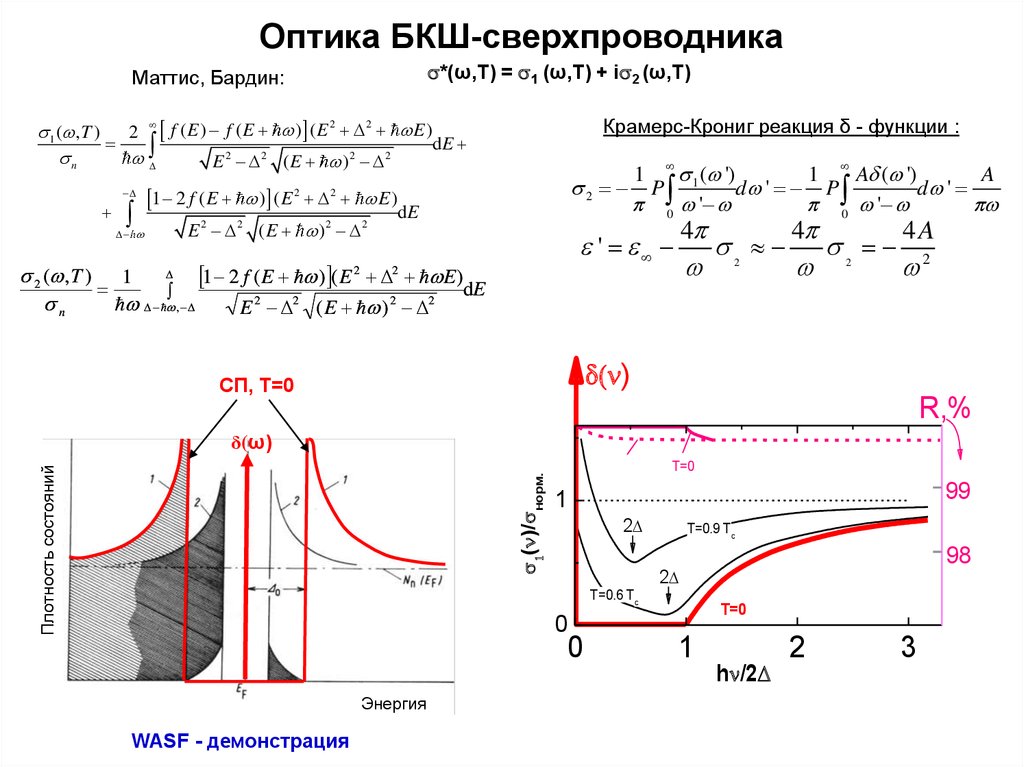
4. Оптика БКШ-сверхпроводника

*(ω,T) = 1 (ω,T) + i 2 (ω,T)
Маттис, Бардин:
2
2
1 ( , T ) 2 f ( E ) f ( E ) ( E D E )
dE
n
D
E 2 D 2 ( E )2 D 2
D
D
1 2 f ( E
) ( E 2 D 2 E )
E 2 D 2 ( E )2 D 2
Крамерс-Крониг реакция δ - функции :
1 ( ')
1
A ( ')
A
2 P
d ' P
d '
0 '
0 '
1
dE
'
D
2 ( , T ) 1
1 2 f ( E ) ( E 2 D2 E )
dE
n
D , D
E 2 D2 ( E ) 2 D2
4
2
4
2
4A
2
)
СП, Т=0
R,%
( )/ норм.
Плотность состояний
δ(ω)
T=0
99
1
2D
T=0.9 Tc
98
2D
T=0.6 Tc
0
0
Энергия
WASF - демонстрация
T=0
1
h /2D
2
3

5.

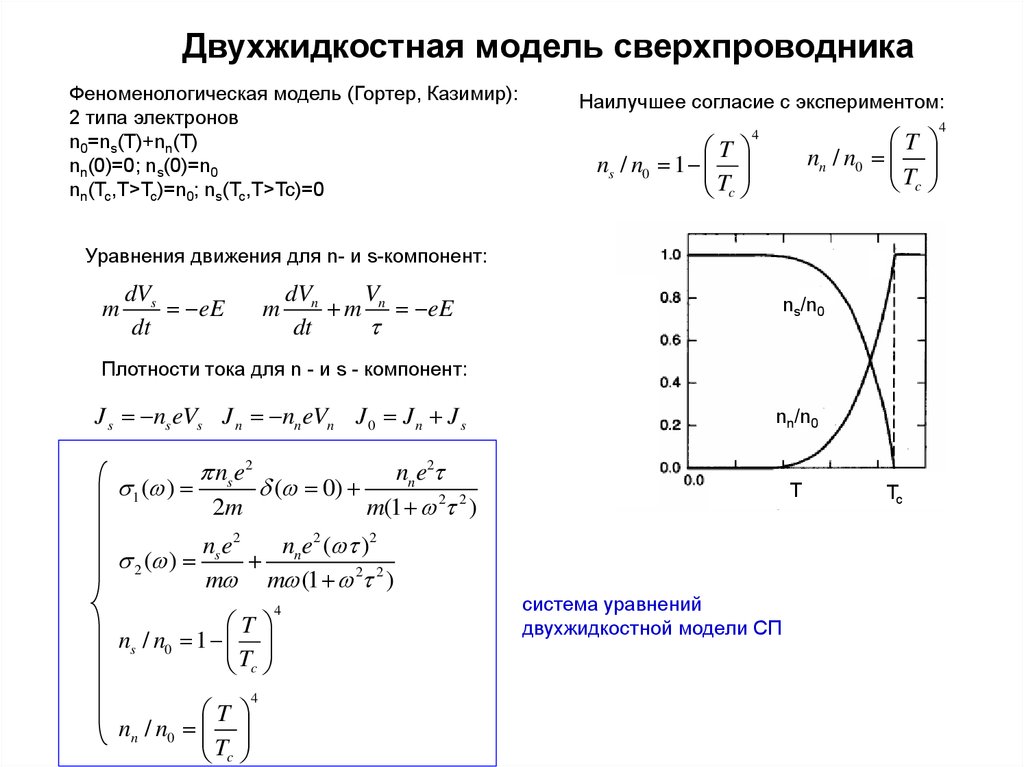
Двухжидкостная модель сверхпроводника
Феноменологическая модель (Гортер, Казимир):
2 типа электронов
n0=ns(T)+nn(T)
nn(0)=0; ns(0)=n0
nn(Tc,T>Tc)=n0; ns(Tc,T>Tc)=0
Наилучшее согласие с экспериментом:
T
ns / n0 1
Tc
T
nn / n0
Tc
4
Уравнения движения для n- и s-компонент:
m
dVs
eE
dt
m
dVn
V
m n eE
dt
ns/n0
Плотности тока для n - и s - компонент:
J s ns eVs J n nn eVn J 0 J n J s
nn/n0
ns e2
nn e2
1 ( )
( 0)
2m
m(1 2 2 )
ns e2
nn e2 ( )2
2 ( )
m m (1 2 2 )
T
ns / n0 1
Tc
T
nn / n0
Tc
4
4
T
система уравнений
двухжидкостной модели СП
Tc
4

6.

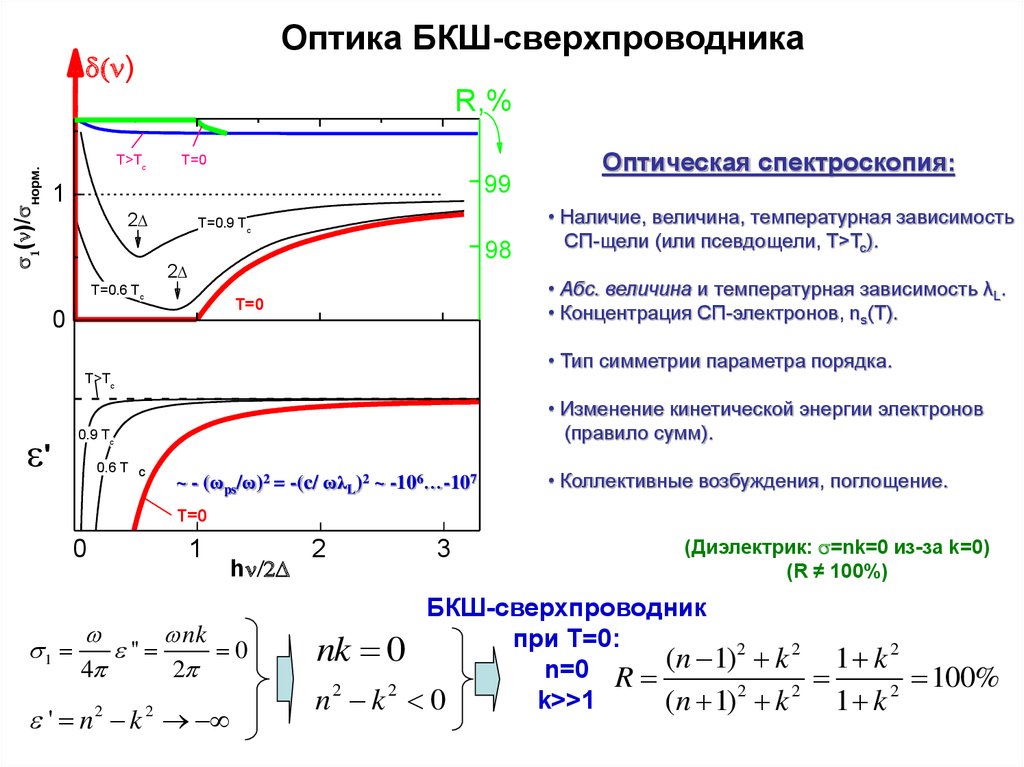
Оптика БКШ-сверхпроводника
)
( )/ норм.
R,%
T>Tc
T=0
99
1
2D
T=0.9 Tc
98
2D
T=0.6 Tc
• Наличие, величина, температурная зависимость
СП-щели (или псевдощели, T>Tc).
• Абс. величина и температурная зависимость λL.
• Концентрация СП-электронов, ns(T).
T=0
0
Оптическая спектроскопия:
• Тип симметрии параметра порядка.
T>Tc
'
• Изменение кинетической энергии электронов
(правило сумм).
0.9 Tc
0.6 T c
~ - (ωps/ω)2 = -(c/ ωλL)2 ~ -106…-107
• Коллективные возбуждения, поглощение.
T=0
0
1
1
h / D
nk
''
0
4
2
' n2 k 2
2
3
(Диэлектрик: =nk=0 из-за k=0)
(R ≠ 100%)
БКШ-сверхпроводник
при Т=0:
2
2
2
nk 0
(
n
1)
k
1
k
n=0 R
100%
2
2
2
2
2
k>>1
n k 0
(n 1) k
1 k

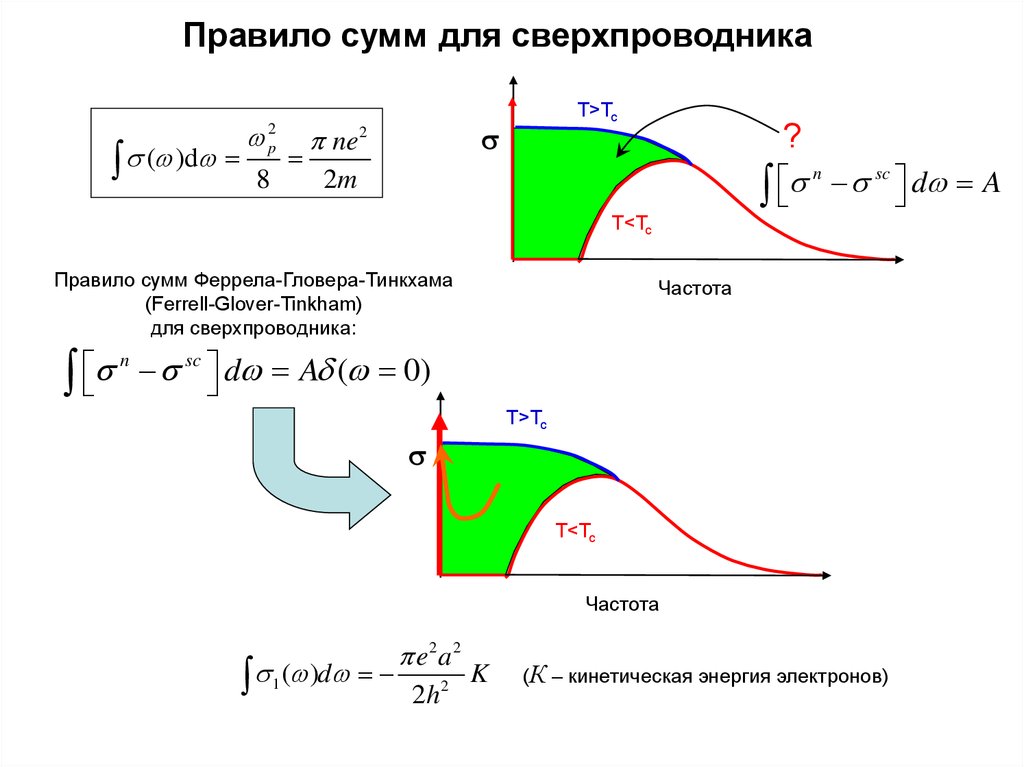
7. Правило сумм для сверхпроводника

( )d
2
p
8
T>Tc
ne2
?
n
sc
d A
2m
T<Tc
Правило сумм Феррела-Гловера-Тинкхама
(Ferrell-Glover-Tinkham)
для сверхпроводника:
Частота
n
sc
d A ( 0)
T>Tc
T<Tc
Частота
( )d
1
e2 a 2
2h
2
K
(К – кинетическая энергия электронов)

8.

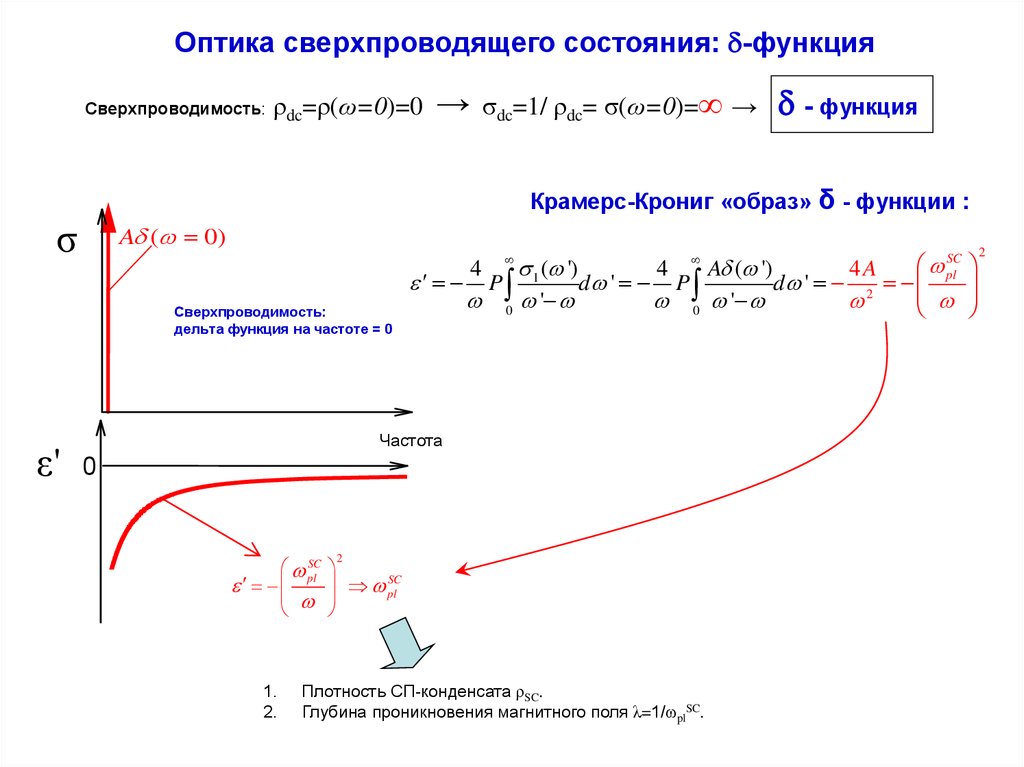
Оптика сверхпроводящего состояния: -функция
Сверхпроводимость:
ρdc=ρ(ω=0)=0
→
σdc=1/ ρdc= σ(ω=0)=∞ →
- функция
Крамерс-Крониг «образ» δ - функции :
σ
A ( 0)
pl
1 ( ')
4
A ( ')
4A
P
d ' P
d ' 2
0 '
0 '
4
Сверхпроводимость:
дельта функция на частоте = 0
ε'
Частота
0
plSC
1.
2.
2
SC
pl
Плотность СП-конденсата ρSC.
Глубина проникновения магнитного поля λ=1/ωplSC.
SC
2

9.

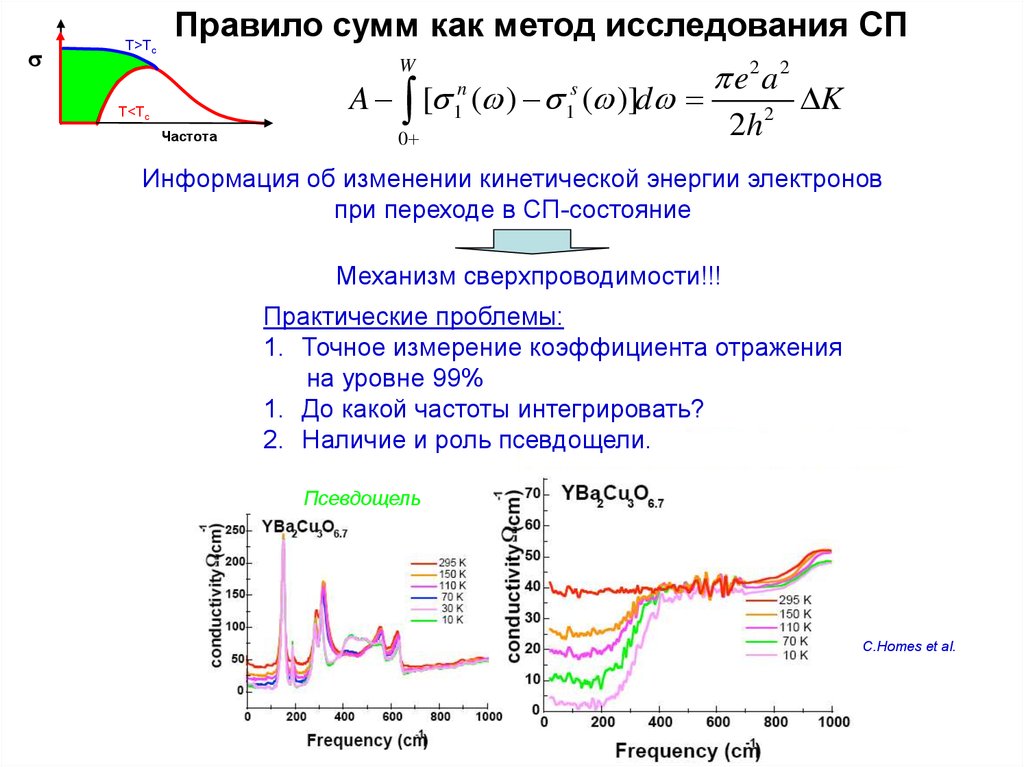
T>Tc
Правило сумм как метод исследования СП
W
A [ ( ) ( )]d
n
1
T<Tc
Частота
s
1
e2 a 2
0
2h
2
DK
Информация об изменении кинетической энергии электронов
при переходе в СП-состояние
Механизм сверхпроводимости!!!
Практические проблемы:
1. Точное измерение коэффициента отражения
на уровне 99%
1. До какой частоты интегрировать?
2. Наличие и роль псевдощели.
Псевдощель
C.Homes et al.

10.

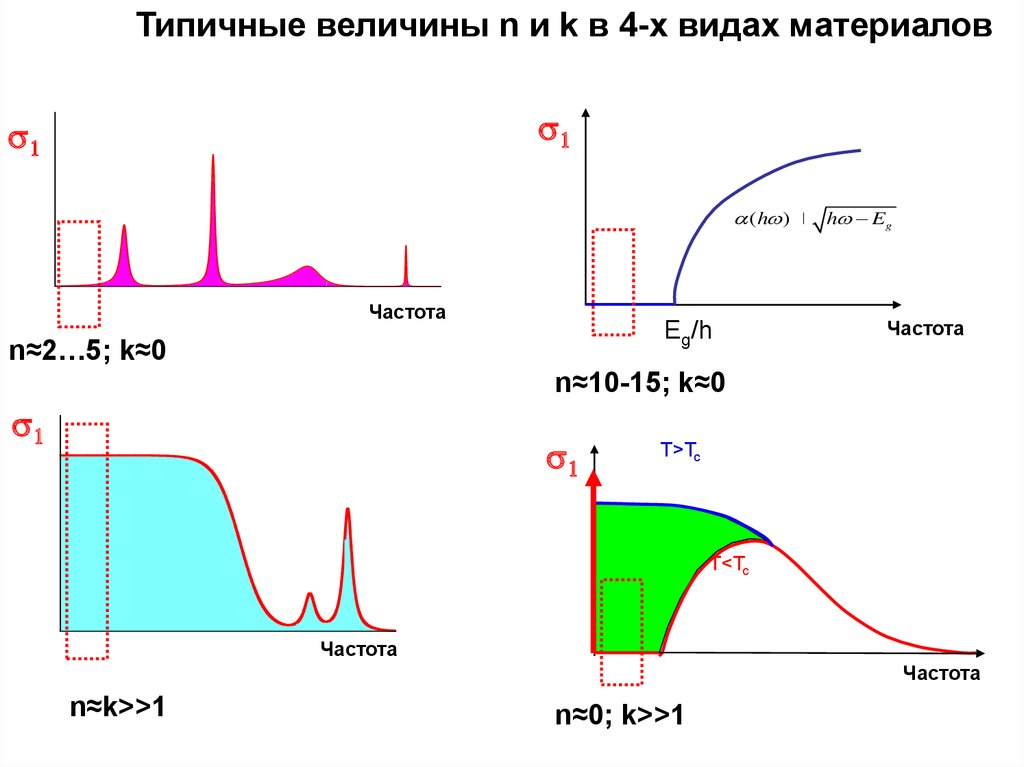
Типичные величины n и k в 4-х видах материалов
(h )
Частота
Eg/h
n≈2…5; k≈0
h Eg
Частота
n≈10-15; k≈0
T>Tc
T<Tc
Частота
Частота
n≈k>>1
n≈0; k>>1