Похожие презентации:
Теория сверхпроводимости
1.
Тема 7.Основы теории сверхпроводимости
2.
Классическая теорияпроводимости
3.
Хейке Каммерлинг-Оннес1911 г. сопротивление ртути
4.
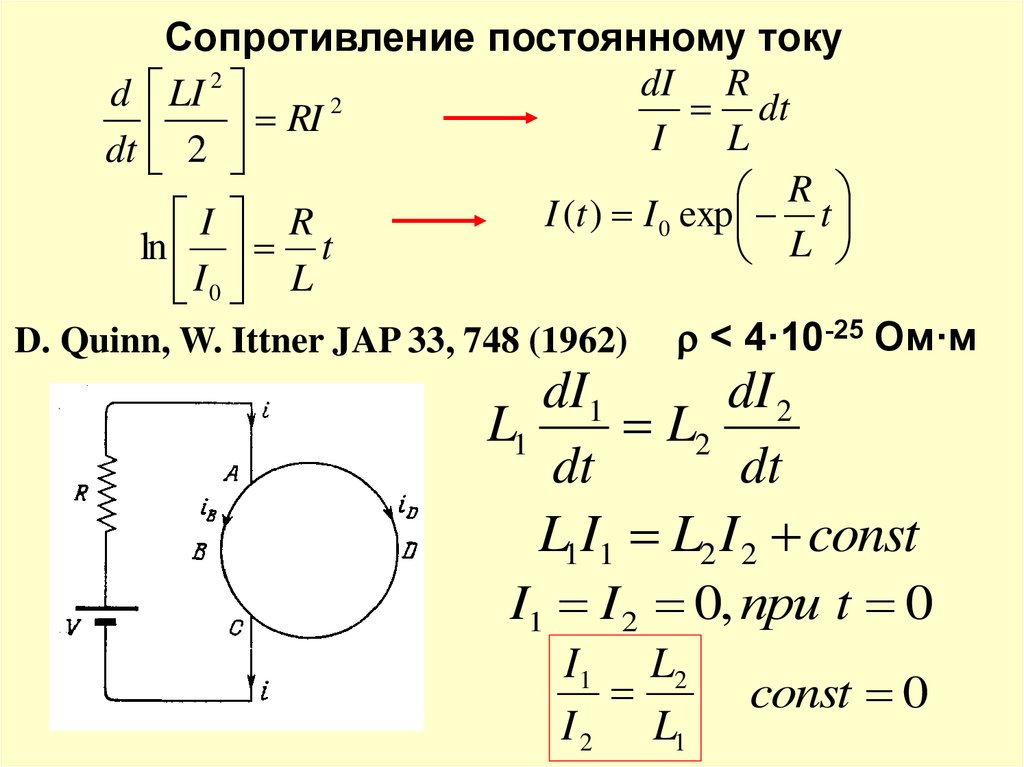
Сопротивление постоянному токуdI R
d LI 2
2
dt
RI
I
L
dt 2
R
I (t ) I 0 exp t
I R
ln t
L
I0 L
D. Quinn, W. Ittner JAP 33, 748 (1962) < 4·10-25 Ом·м
dI1
dI 2
L1
L2
dt
dt
L1I1 L2 I 2 const
I1 I 2 0, при t 0
I1 L2
I 2 L1
const 0
5.
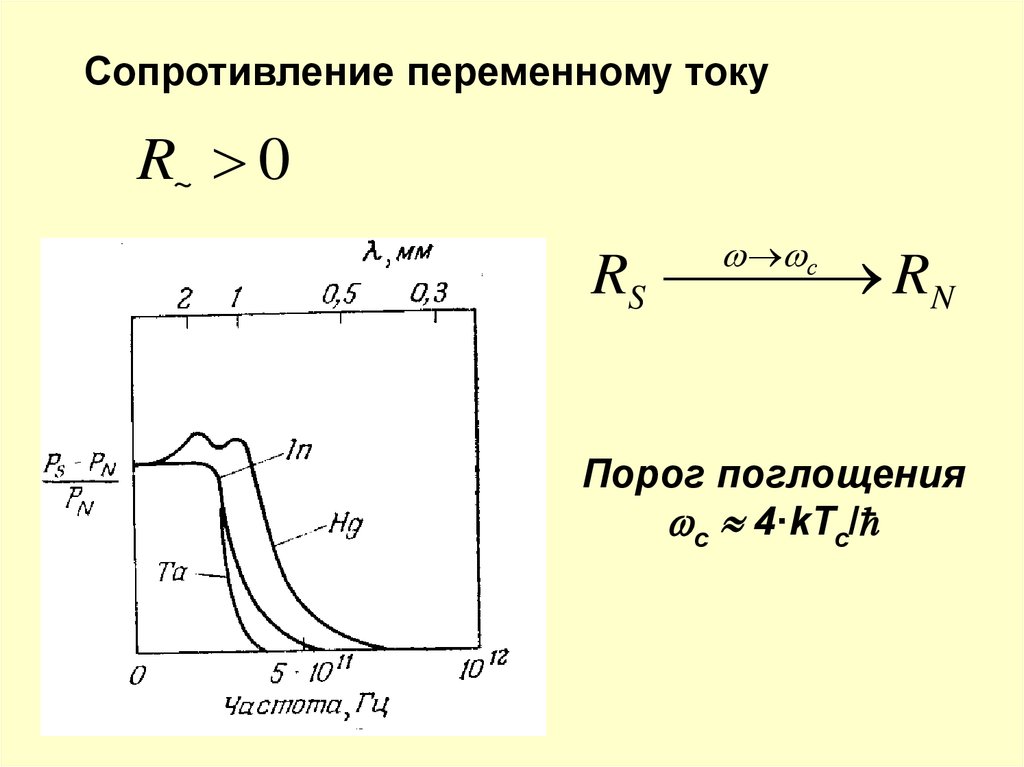
Сопротивление переменному токуR~ 0
с
RS RN
Порог поглощения
c 4·kTc/
6.
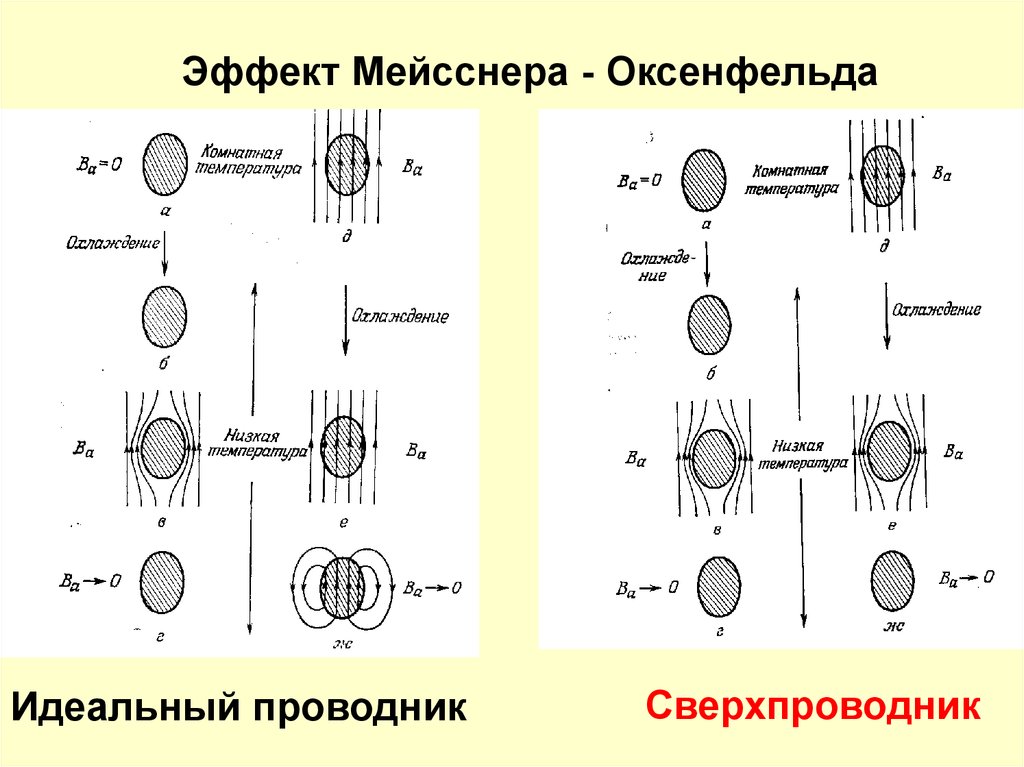
Эффект Мейсснера - ОксенфельдаИдеальный проводник
Сверхпроводник
7.
Электродинамика идеальных проводниковJ s e vs ne
dvs
me
e E
dt
dJ s e ns E
dt
me
2
dB
dD
rot E rot H J
dt
dt
div B 0
1
dD
rot B 0 J s
dt
0
dD
J s
dt
8.
dBrot E
dt
me dJ s
E
2
e ns dt
me
dB
dJ s
2
rot
dt e ns
dt
rot B 0 J s
dB
me
dB
2
rot rot
dt
e ns 0
dt
9.
dBme
dB
2
rot rot
dt
e ns 0
dt
me
2
e ns 0
dB
dB
rot rot
dt
dt
dB
dB dB
rot rot div
dt dt
dt
10.
dBdB
dB 1 dB
dt
dt
dt dt
B
2
B0
x
d dB 1 dB
2
dx dt dt
dB dB0
x
exp(
)
dt
dt
11.
Теория ЛондоновB
B
B B0 exp(
me
B 2
rot J s
e ns
x
)
me
L 2
e ns 0
dJ s e ns E
dt
me
2
Элем.
Al
Cd
In
Nb
Pb
Sn
Tl
L, Å
500
1300
640
470
390
510
920
12.
BB0
x
B0
x
x
J
exp( ) J 0 exp( )
L
L
0 L
dB
0 J y
dx
rot B 0 J s
B Bc
T Tc
T
L (T ) L (0) 1
Tc
1
4
2
13.
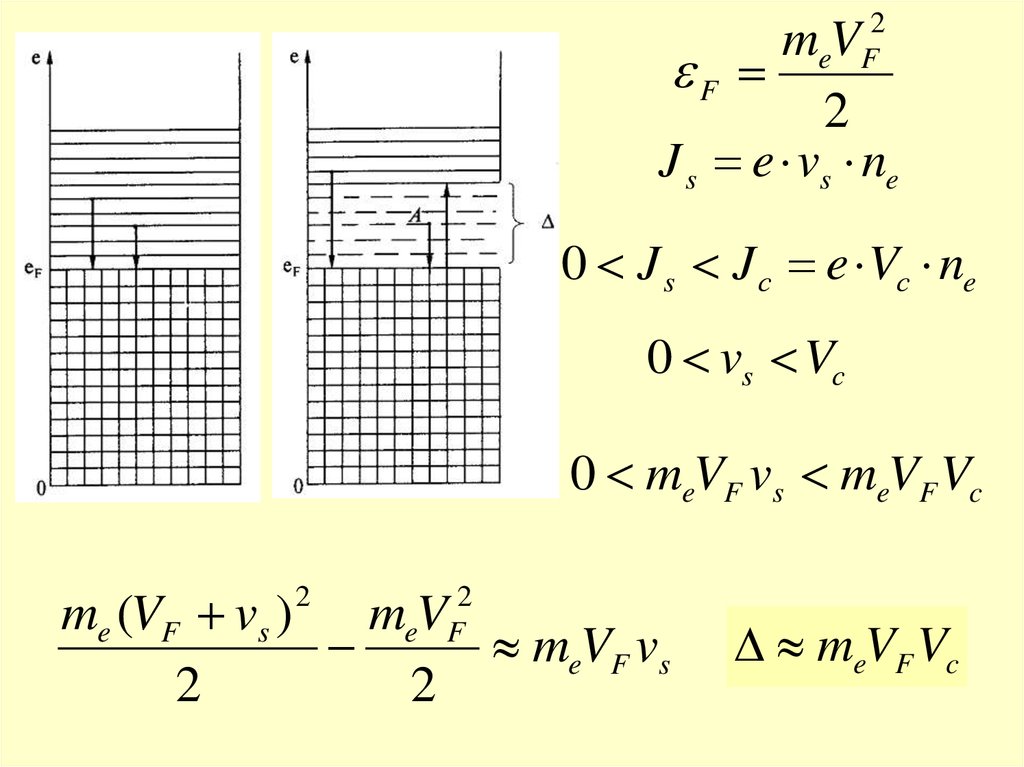
2e F
mV
F
2
J s e vs ne
0 J s J с e Vс ne
0 vs Vс
0 meVF vs meVF Vc
me (VF vs ) m V
meVF vs
2
2
2
2
e F
meVF Vc
14.
1)Критическая
температура
разрушения
сверхпроводимости
Tc
составляет
несколько
Кельвинов, следовательно, тепловая энергия kTc
необходимая
для
разрушения
взаимодействия
электронов имеет порядок величины 10-4 –10-5 эВ.
2) Тоже значение энергии получается из частотной
зависимости поглощения электромагнитных волн
(Порог поглощения 1010 - 1011 Герц).
3) И, наконец, эту энергию можно получить из
термодинамических соображений. Разница между
свободными энергиями металла и сверхпроводника,
приходящаяся на 1 см3, равна Hc2/8 . Подставляя в эту
формулу типичное значение критического поля Hc=103
эрстед, мы получаем Hc2/8 ~ 105 эрг/см3. В одном
кубическом сантиметре содержится ~1022 электронов, значит,
на один электрон приходится энергия 10-17 эрг ~ 6х10-5 эВ.
15.
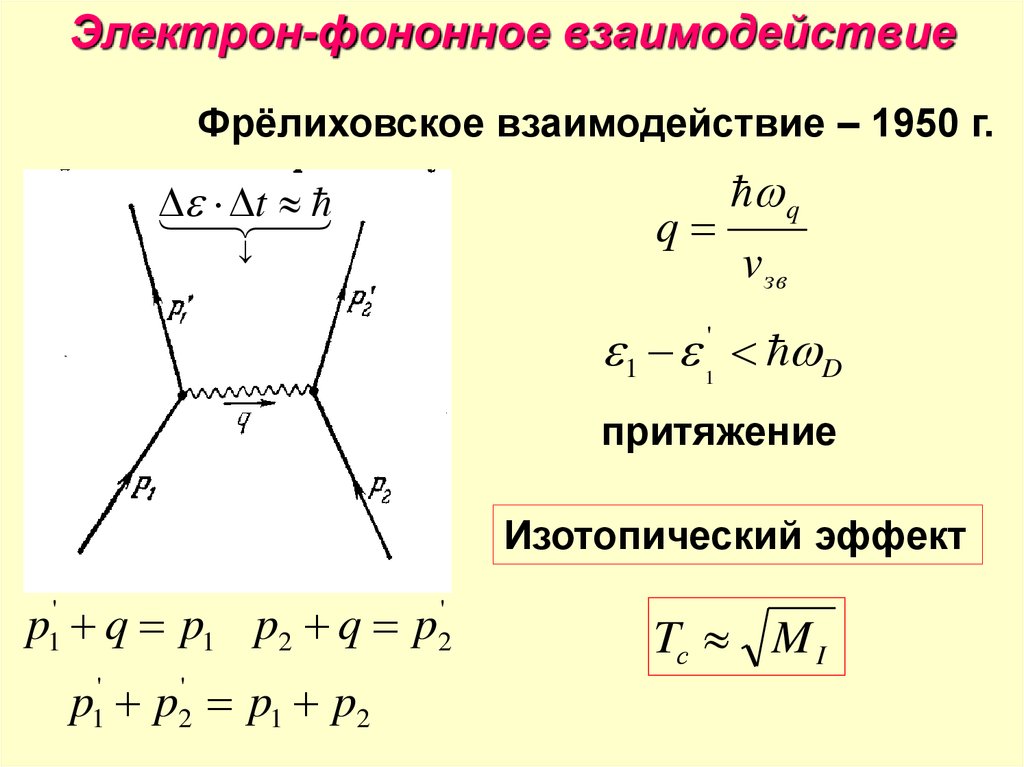
Электрон-фононное взаимодействиеФрёлиховское взаимодействие – 1950 г.
t
q
q
v зв
1 D
'
1
притяжение
Изотопический эффект
p q p1 p2 q p
'
2
'
1
p1' p2' p1 p2
Tс M I
16.
Куперовские парыСфера Ферми
Добавим 2 невзаимодействующих
электрона
(r1, r2 , p1, p2 ) r1, p1 r2 , p2
Учтем взаимодействие электронов
Φ( r1 , r2 , p1 , p2 )
ai , j ri , pi rj , p j
i, j
1
2
| ai , j | вероятность иметь
2
pF (2me F ) электроны в cостояниях p и p
i
j
17.
Куперовские парыВ процессе рассеяния электроны
взаимодействуют между собой и, если это
взаимодействие отвечает притяжению, то
результирующая потенциальная энергия будет
отрицательна.
За период времени, в течение которого
происходит многократное рассеяние энергия
двух электронов уменьшается на эту,
усредненную по времени отрицательную
потенциальную энергию. Величина этого
уменьшения пропорциональна числу
происходящих актов рассеяния - т.е. числу
способов, которыми можно выбрать два члена из
волновой функции .
18.
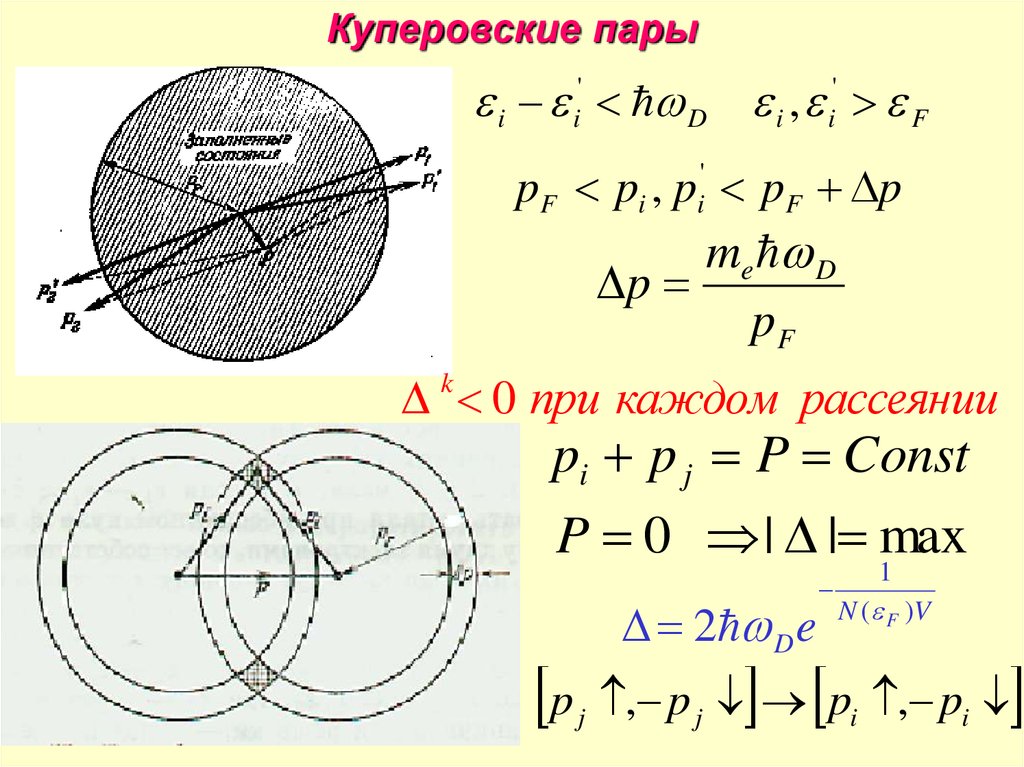
Куперовские парыi i' D i , i' F
pF pi , pi' pF p
me D
p
pF
0 при каждом рассеянии
k
pi p j P Const
P 0 | | max
p
2 D e
j
1
N ( F )V
, p j pi , pi
19.
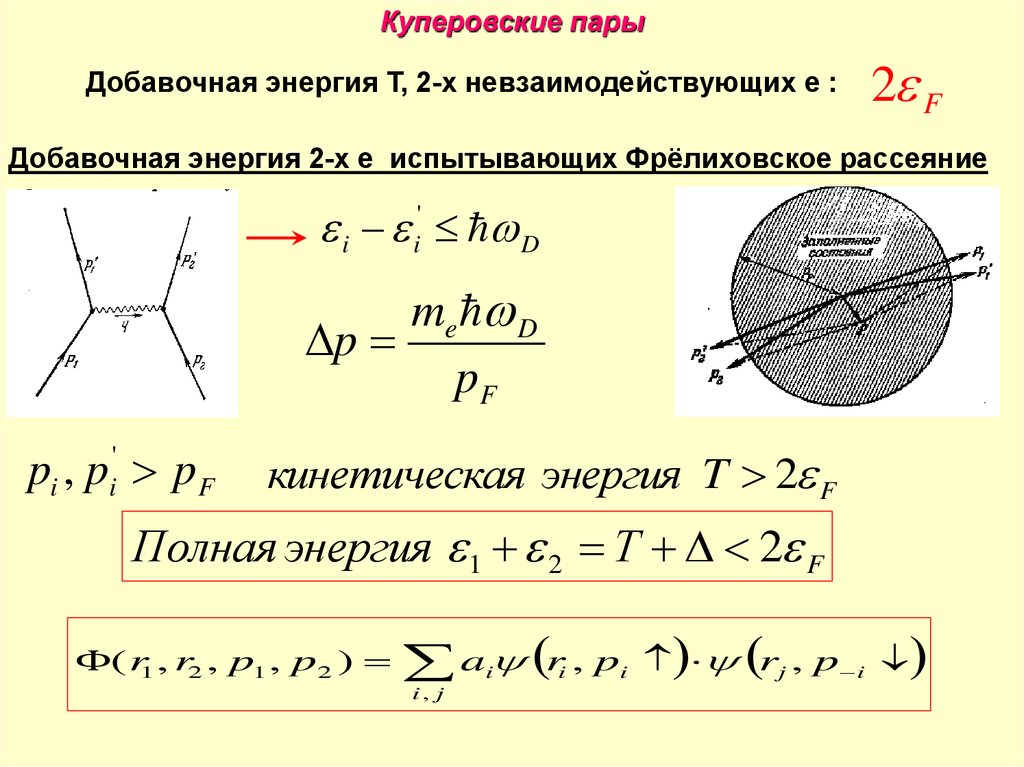
Куперовские парыДобавочная энергия T, 2-x невзаимодействующих e :
2 F
Добавочная энергия 2-x e испытывающих Фрёлиховское рассеяние
i i' D
me D
p
pF
pi , p pF
'
i
кинетическая энергия T 2 F
Полная энергия 1 2 Т 2 F
Φ( r1 , r2 , p1 , p2 )
a r , p
i
i, j
i
i
rj , p i
20.
Учет взаимодействия 2 электронов даетвыигрыш в энергии!!!
Может быть нужно учесть взаимодействие
между большим количеством электронов,
3-мя, 4-мя, ….?
И мы получим еще больший выигрыш в
энергии?
21.
БКШГлавное предположение этой теории
заключается в том, что единственным
существенным для сверхпроводимости
взаимодействием
является
взаимодействие между двумя любыми
электронами,
которые
образовали
куперовскую
пару.
Влияние
всех
остальных электронов заключается лишь
в том, что вследствие принципа Паули
число состояний, в которые могут
рассеиваться взаимодействующие пары,
ограничено, поскольку некоторые из
состояний уже заполнены.
22.
Соображения Купера можно применить к любой паре е вблизи уровня ФермиG (rn.... ) r1 , r2 r3 , r4 ....... rn , rn 1
Мы можем рассматривать каждую пару как квазичастицу,
подчиняющеюся статистике Бозе-Эйнштейна
Образование, каждой новой пары уменьшает
полную энергию системы электронов
Вопрос:
Могут ли все электроны образовать пары?
НЕТ!, потому что количество незаполненных
состояний (p, -p ) уменьшается
с ростом количества пар
Выигрыш в энергии ~ числу актов рассеяния в ед. времени
23.
Энергетическая щельОсновное состояние сверхпроводника – идеальный газ Куперовских пар
Что будет, если мы внесем в него возбуждение?
( + T или h )
Как описать возбужденное состояния сверхпроводника?
Элементарное возбуждение это разрушение одной К.П.
Eвозб [( i F )2 2 ]1/ 2 [( j F )2 2 ]1/ 2
Появляется 2 электрона, в состояниях с импульсами p ,
причем дополнительные состояния -p не заполнены
2
Т.е. в результате возбуждения уменьшается число
состояний, в которые могут рассеиваться оставшиеся К.П.
Tc
2 (T 0) 3,5kTc T
0
24.
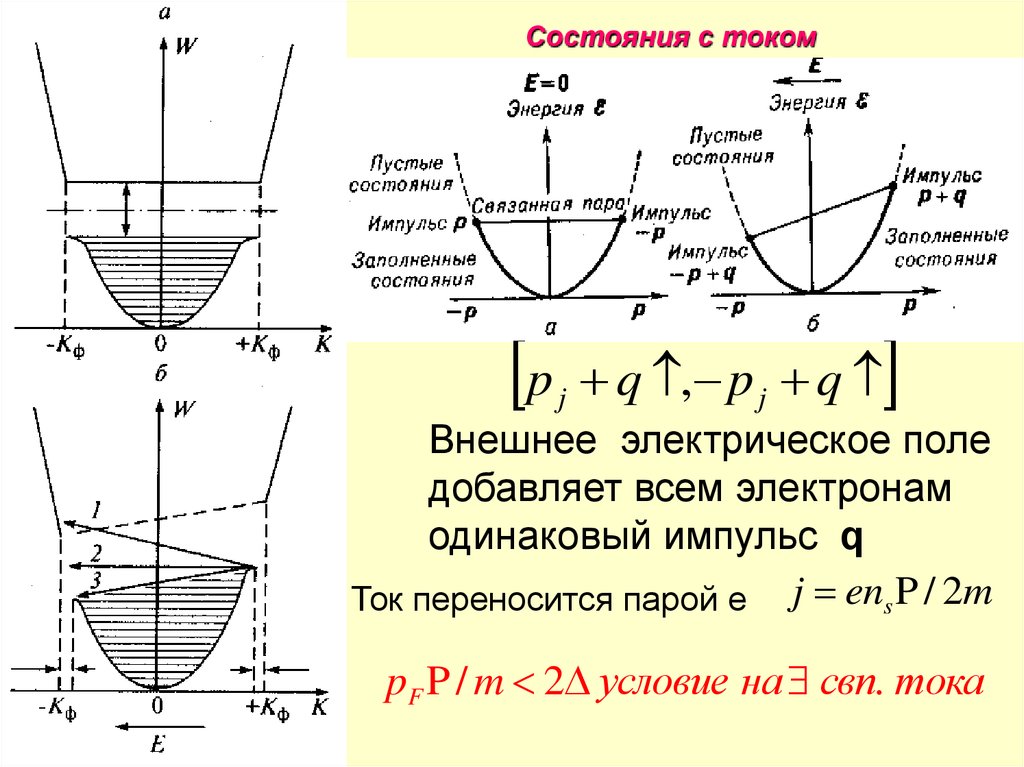
Состояния с токомp
j
q , p j q
Внешнее электрическое поле
добавляет всем электронам
одинаковый импульс q
Ток переносится парой e j ens P / 2m
pF P / m 2 условие на свп. тока
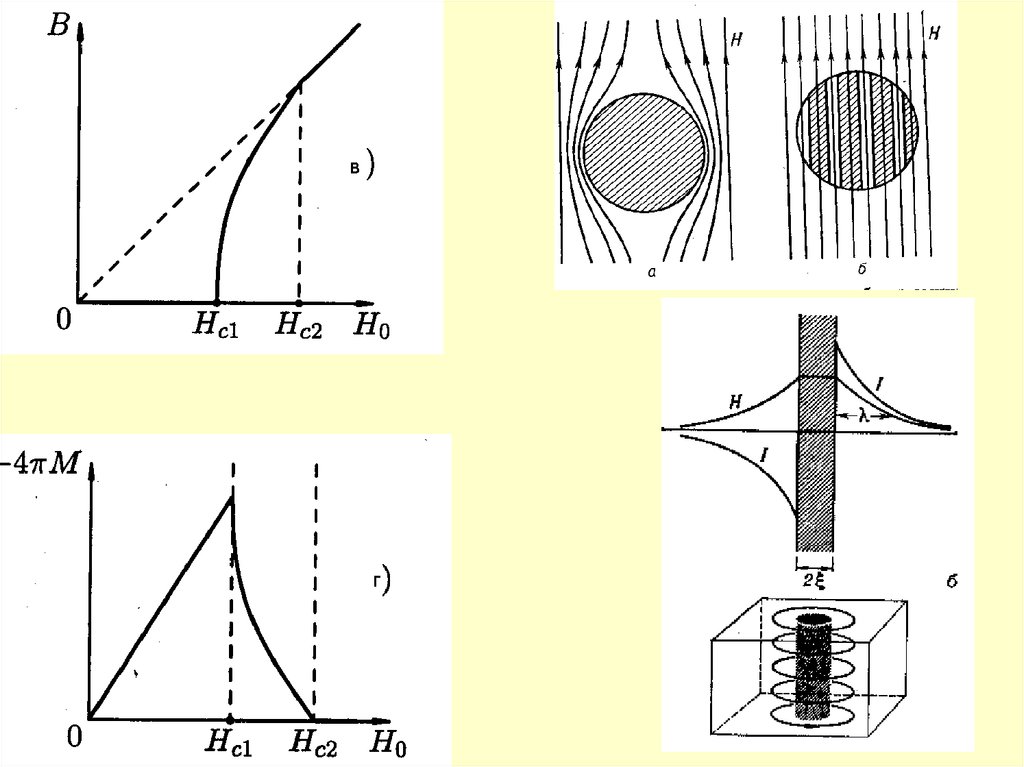
25.
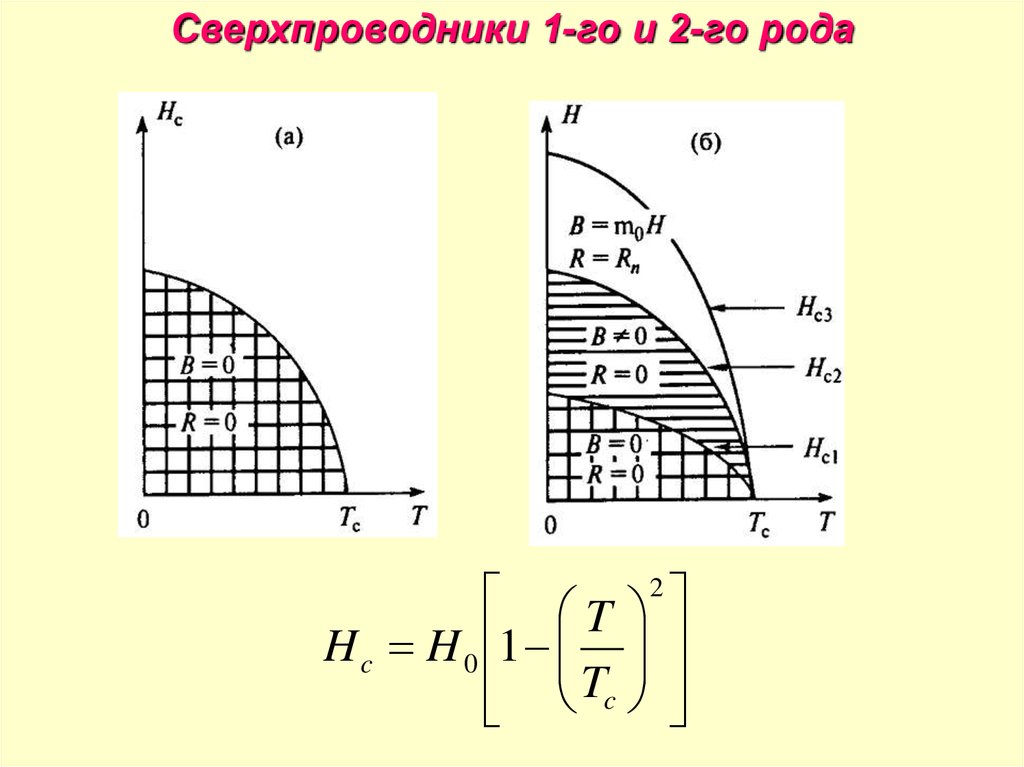
Сверхпроводники 1-го и 2-го родаT 2
H c H 0 1
Tc
26.
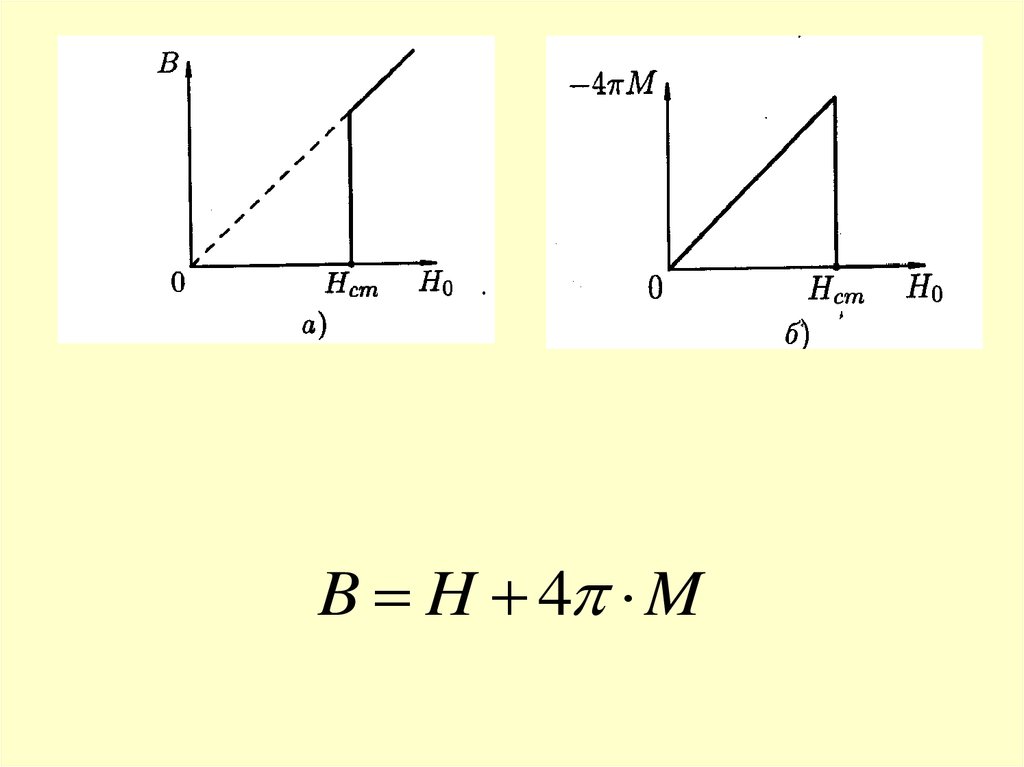
B H 4 M27.
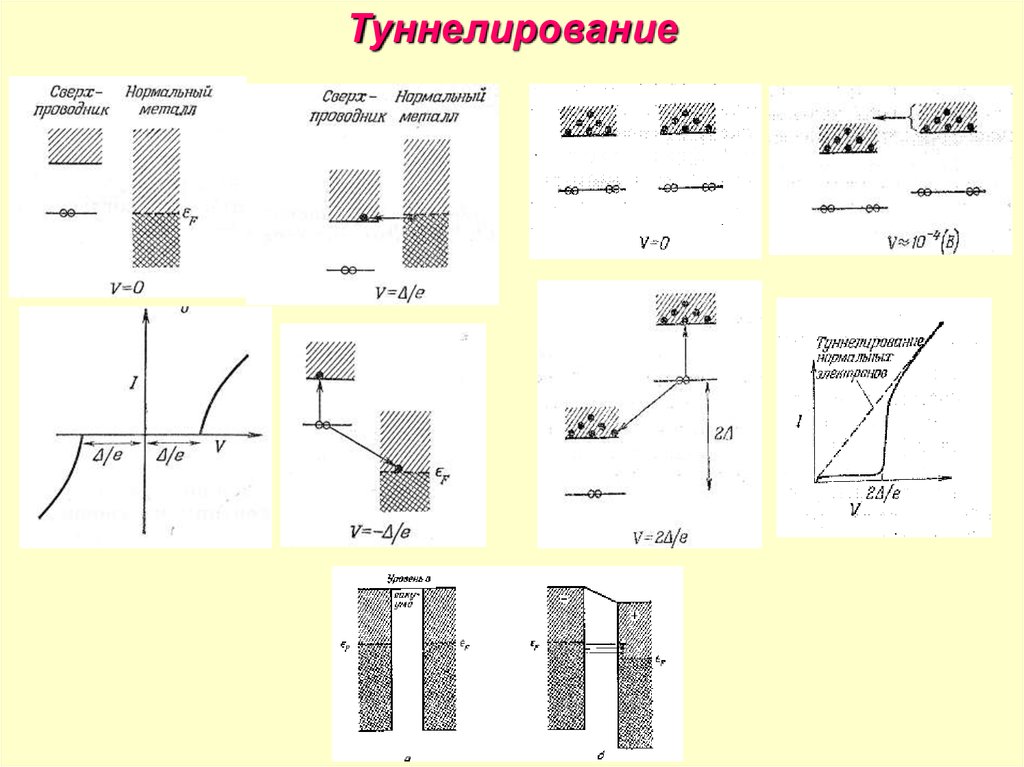
28.
Туннелирование29.
Эффекты Джозефсонаr, t nc exp i (r, t )
1(x) = (x)·nc11/2·exp{i· 1(x)}
2(x) = (x)·nc21/2·exp{i· 2(x)}
J J max sin( )
I Im( (x) (x))
nc11/2·nc21/2·sin( 1(x)- 2(x)).
30.
0 HLdm
J J max
sin( 2 m)
J max
2
0
0 HLd
0
2
sin(
)
0
2
0
31.
СКВИД - Superconducting Quantum Interference DeviceJ ( ) 2 J max cos(
0
)
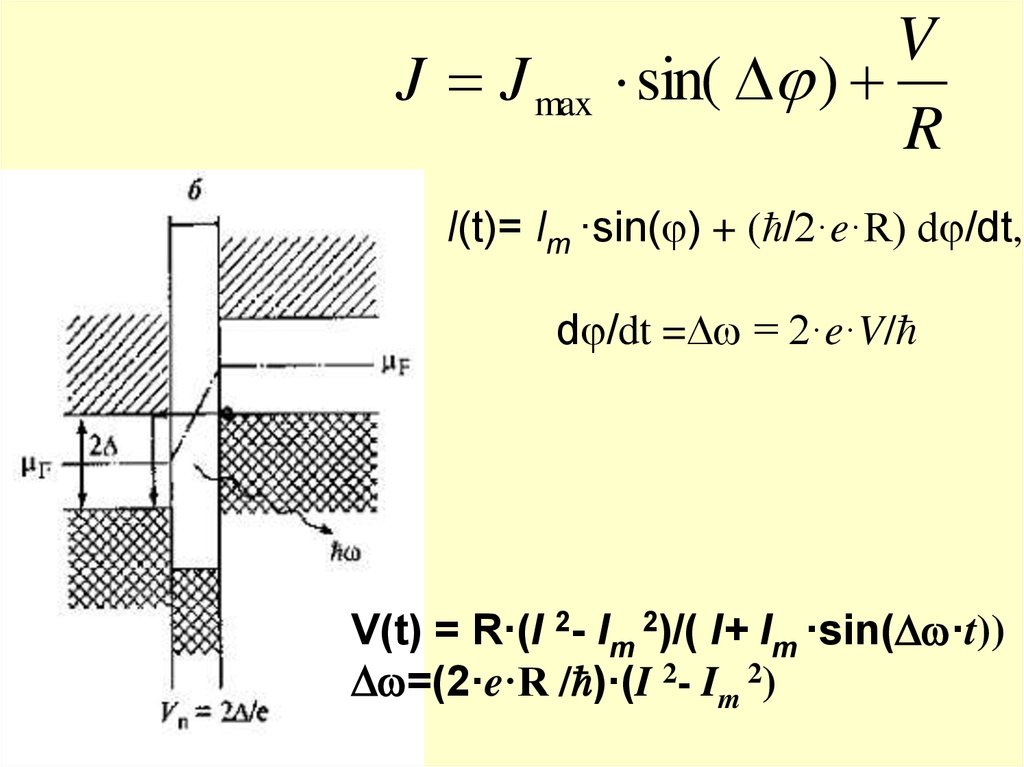
32.
J J maxV
sin( )
R
I(t)= Im ·sin( ) + ( /2·e·R) d /dt,
d /dt = = 2·e·V/
V(t) = R·(I 2- Im 2)/( I+ Im ·sin( ·t))
=(2·e·R / )·(I 2- Im 2)




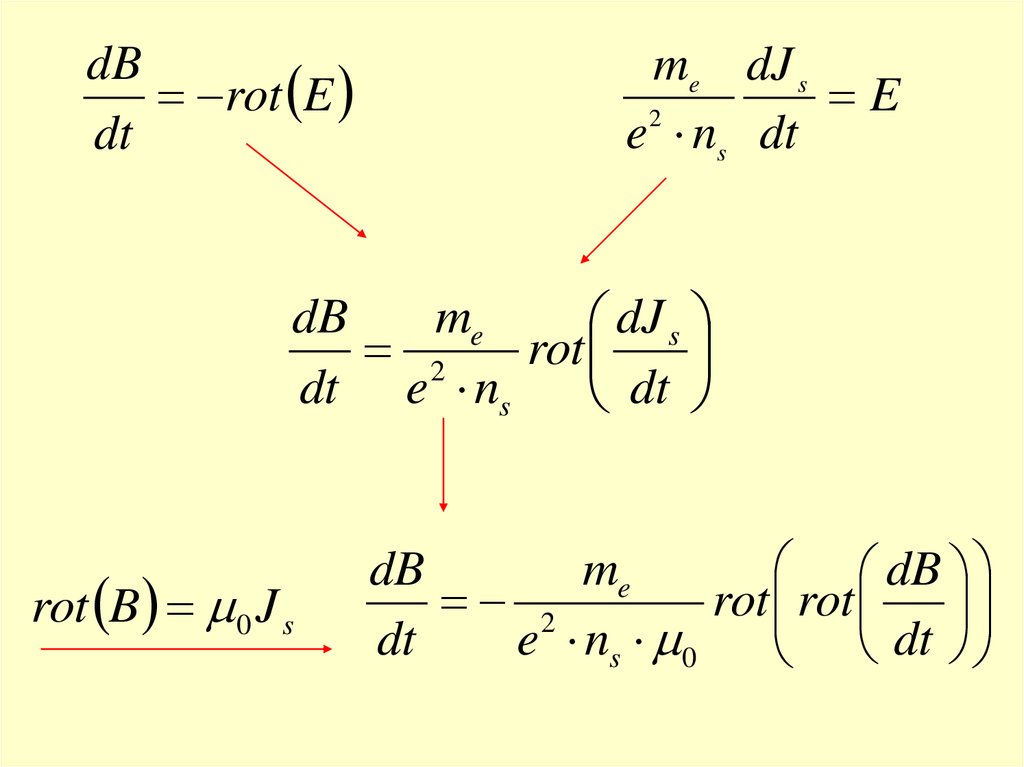

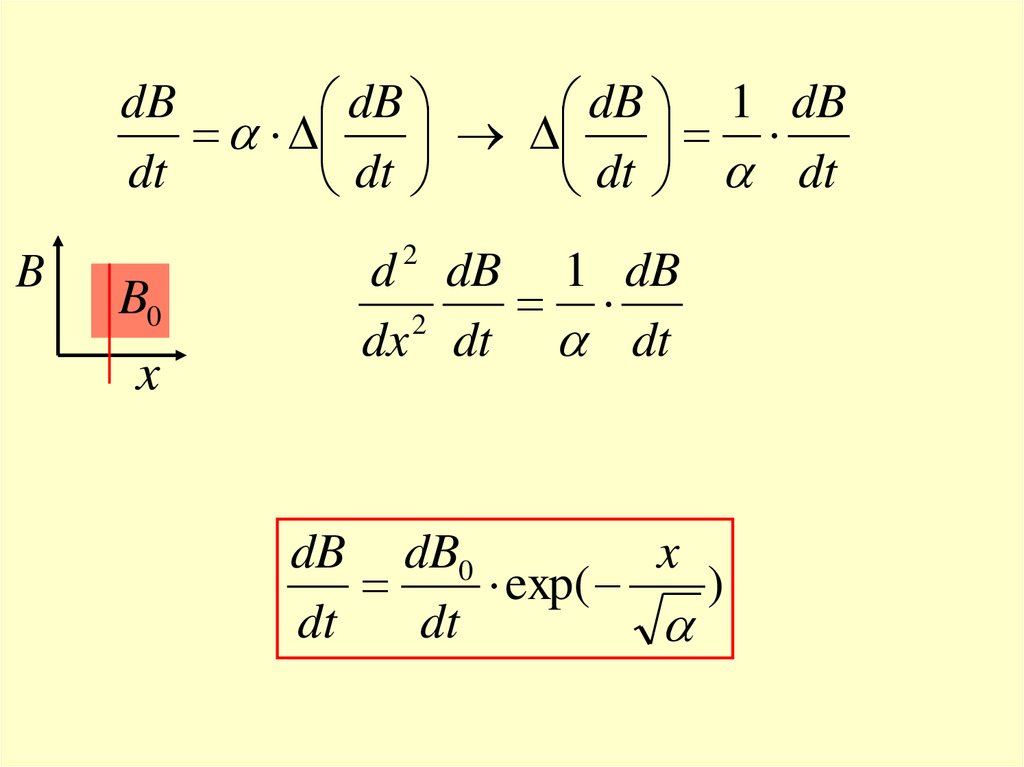












 Физика
Физика








