Похожие презентации:
Модели эксплуатации на основе метода динамики средних
1. Моделирование систем и процессов
Лекция 6.Модели эксплуатации на основе метода
динамики средних
2. Сущность метода динамики средних
При рассмотрении метода динамики среднихвозможны следующие случаи:
сложная система состоит из большого числа
однородных элементов, каждый из которых может
переходить случайным образом из состояния в
состояние;
интенсивность потоков зависит от численности
состояний;
численность состояний изменяется за счет
внешних воздействий;
система состоит из большого числа
неоднородных элементов.
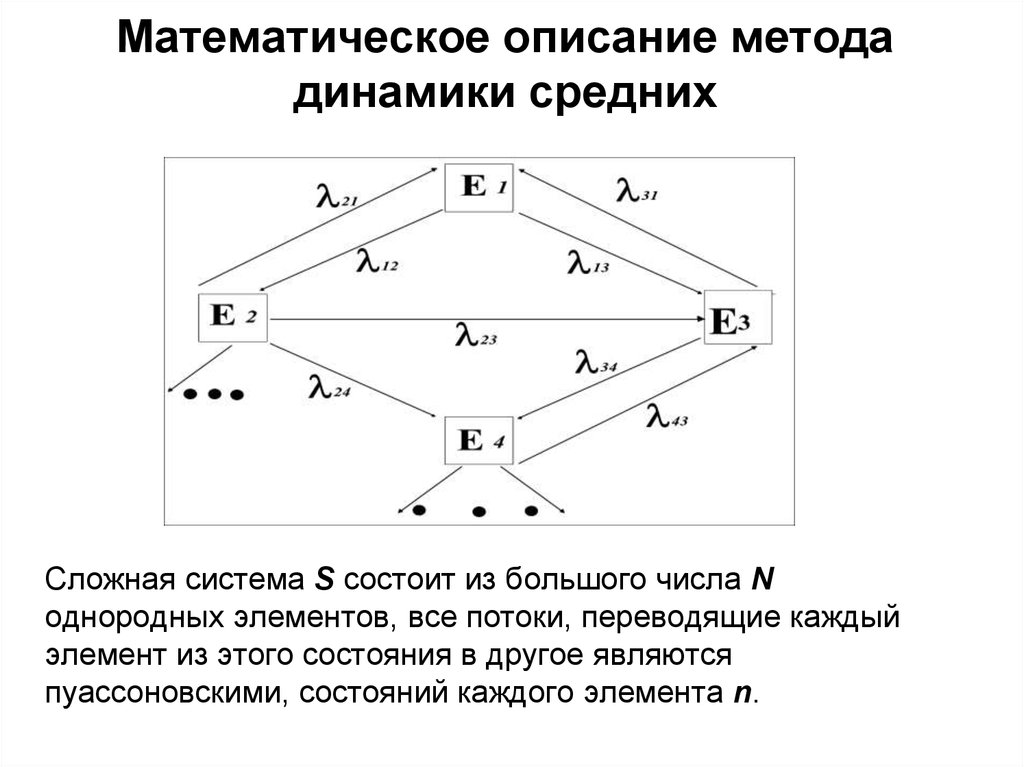
3. Математическое описание метода динамики средних
Cложная система S состоит из большого числа Nоднородных элементов, все потоки, переводящие каждый
элемент из этого состояния в другое являются
пуассоновскими, состояний каждого элемента n.
4. Математическое описание метода динамики средних
В некоторый момент t число элементов системы Xi(t),находящихся в состоянии Ei будет величиной
случайной.
X 1 (t ) X 2 (t ) ... X k (t ) ... X k (t ) N
Общее число состояний равно сумме величин по всем
элементам
X k (t ) X k(1) (t ) X k( 2) (t ) ... X k(i ) (t ) .... X k( N ) (t )
N
(i )
X
K (t )
i 1
Вероятность нахождения элемента в состоянии Ek –
Pk(t)
Математическое ожидание случайной величины Xk(t)
M X k(i ) (t ) 0 (1 Pk (t )) 1 Pk (t ) Pk (t )
5. Математическое описание метода динамики средних
Математическое ожидание общей численностиэлементов, находящихся в состоянии Ei
N
N
i 1
i 1
mk (t ) M ( X k(i ) (t )) Pk (t ) NPk (t )
Для значений дисперсий получаем следующие
выражения
Dk (t ) NPk (t )(1 Pk (t ))
σ k (t ) DK (t )
Таким образом, если известны вероятности всех
состояний одного элемента то могут быть определены
и средние численности состояний, их дисперсии и
соответственно среднеквадратические отклонения
6.
dP1 (t )( 12 13 ) P1 (t ) 21P2 (t )
dt
dNp1 (t )
( 12 13 ) NP1 (t ) 21 NP2 (t )
dt
dP2 (t )
12 P1(t ) 21P2 (t ) 32 P3 (t ) dNp2 (t ) 12 NP1(t ) 21NP2 (t ) 32 NP3 (t )
dt
dt
dP3 (t )
13 P1 (t ) 32 P3 (t )
dt
dNP3 (t )
13 NP1 (t ) 32 NP3 (t )
dt
mk (t )
Dk (t ) mk (t )(1
)
N
k (t ) Dk (t ),
dmi (t )
12 m1 (t ) 21m2 (t ) 32 m3 (t )
mk
mk
dt
) (
),
P( X k ( , )) (
k
dm3 (t )
k
13 m1 (t ) 32 m3 (t )
dt
dmi (t )
( 12 13 )m1 (t ) 21m2 (t )
dt
7. Применение уравнений динамики средних для решения эксплуатационных задач
Пример 1Парк авиационного предприятия состоит из N
однотипных самолетов. Каждый из самолетов может
находиться в одном из двух состояний: исправен E1,
неисправен и находится в ремонте E2
N=100
λ=10-3
μ=4.2x10-3
m1 (t )
m1 (t ) m2 (t )
t
m2 (t )
m2 (t ) m1 (t )
t
8.
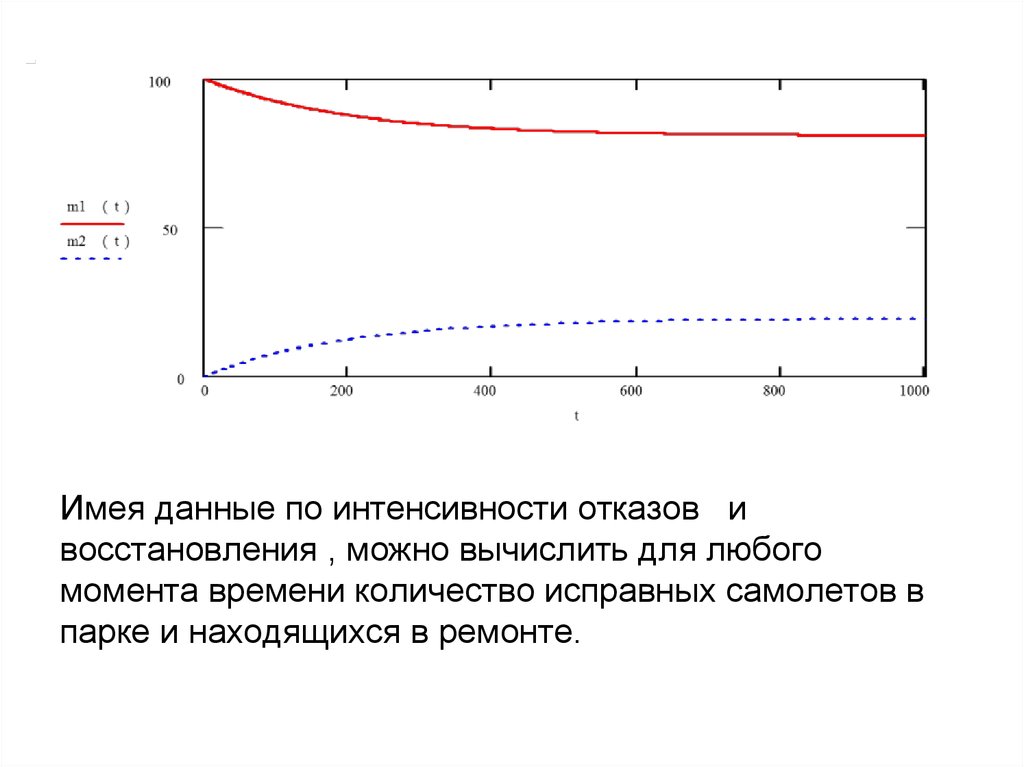
Имея данные по интенсивности отказов ивосстановления , можно вычислить для любого
момента времени количество исправных самолетов в
парке и находящихся в ремонте.
9.
Пример 2Парк самолетов состоит из N однотипных ЛА, возможные
реальные состояния любого ЛА парка:
• E1 - ЛА находится в рейсе;
• E2 - проходит периодическое техническое обслуживание;
• E3 - проходит оперативное техническое обслуживание по форме
А(Ф-А);
• E4 - исправный ЛА находится в ожидании рейса;
• E5 - проходит оперативное техническое обслуживание по Ф – Б;
• E6 - находится в ремонте.
10.
Система дифференциальных уравнений, описывающаяизображенный размеченный граф состояний
dm1 (t )
12 (t ) 13 (t ) 15 (t ) 16 (t ) m1 (t ) 41 (t )m4 (t ),
dt
dm2 (t )
12 (t )m1(t ) 23 (t )m2 (t ),
dt
dm3 (t )
13 (t )m1 (t ) 23 (t ) m2 (t ) 63 (t )m6 (t ) 34 (t )m3 (t ),
dt
dm3 (t )
13 (t )m1 (t ) 23 (t ) m2 (t ) 63 (t )m6 (t ) 34 (t )m3 (t ),
dt
dm5 (t )
15 (t ) m1 (t ) 54 (t ) m5 (t ),
dt
dm6 (t )
16 (t ) m1 (t ) 63 (t ) m6 (t )
dt
6
m (t ) N
i 1
i








 Математика
Математика








