Объем. Цилиндр, призма

1.

2.

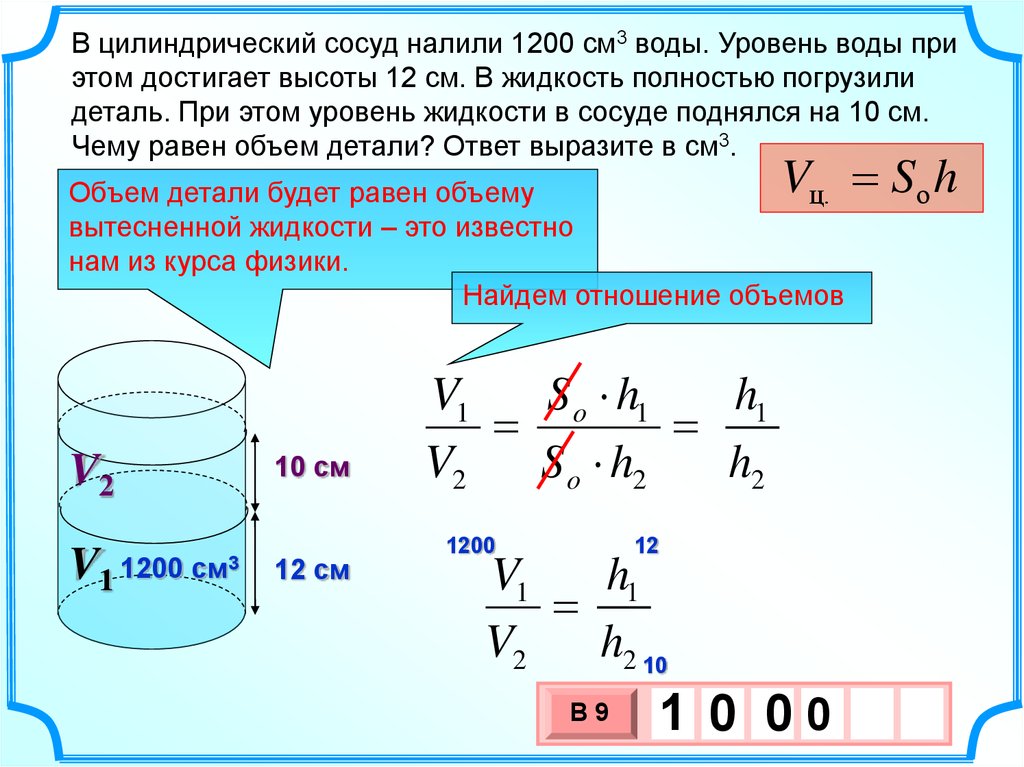
В цилиндрический сосуд налили 1200 см3 воды. Уровень воды при
этом достигает высоты 12 см. В жидкость полностью погрузили
деталь. При этом уровень жидкости в сосуде поднялся на 10 см.
Чему равен объем детали? Ответ выразите в см3.
V Sо h
Объем детали будет равен объему
ц.
вытесненной жидкости – это известно
нам из курса физики.
Найдем отношение объемов
10 см
V2
V1 1200
см3
12 см
S o h1
V1
h1
V2
S o h2
h2
1200
12
V1
h1
V2
h2 10
В9
1 0 00
3
10 х
х

3.

В цилиндрическом сосуде уровень жидкости достигает 27 см. На
какой высоте будет находиться уровень жидкости, если ее перелить во
второй сосуд, диаметр которого в 3 раза больше первого?
Ответ выразите в сантиметрах.
2
d
h1
S1 h1
2
V1
2
S
h
V2
3d
2 2
h2
2
So r 2
V
27 см
d
d2
h1
h1
4
2
9d
9h2
h2
4
Найдем отношение
Объем жидкости
объемов
не
изменился, т.е. V1=V2
1
27
V1
h1
9h2
1 V2
h2
V
3d
В9
3
1
27
=
1
3
10 х
9h
х

4.

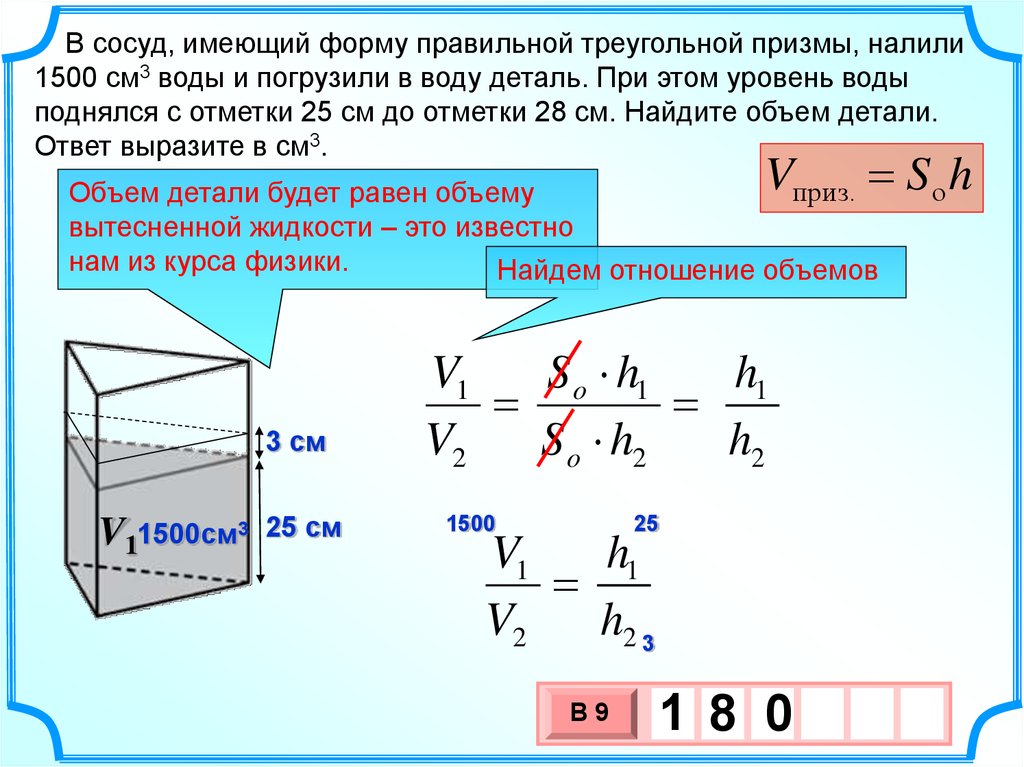
В сосуд, имеющий форму правильной треугольной призмы, налили
1500 см3 воды и погрузили в воду деталь. При этом уровень воды
поднялся с отметки 25 см до отметки 28 см. Найдите объем детали.
Ответ выразите в см3.
V
Sо h
приз.
Объем детали будет равен объему
вытесненной жидкости – это известно
нам из курса физики.
Найдем отношение объемов
3 см
V11500см3
25 см
S o h1
V1
h1
V2
S o h2
h2
1500
25
V1
h1
V2
h2 3
В9
1 8 0
3
10 х
х

5.

В сосуд, имеющий форму правильной треугольной призмы, налили
воду. Уровень воды достигает 16 см. На какой высоте будет находиться
уровень воды, если ее перелить в 1другой такой же сосуд, у которого
сторона основания в 4 раза больше,
чем
у первого?
S = ab
sin
a
Ответ выразите в сантиметрах. 2
16 см
V
a
1
0
a a sin 60 h1
V1
h1
S
h
2
1
1
V2
1
16h2
0
S 2 h2
4a 4a sin 60 h2
2
Найдем отношение
Объем жидкости
объемов
не
изменился, т.е. V1=V2
a
1
16
V1
h1
16h2
1 V2
4a V
h
4a
В9
1
1
16
=
1
3
10 х
16h
х

6.

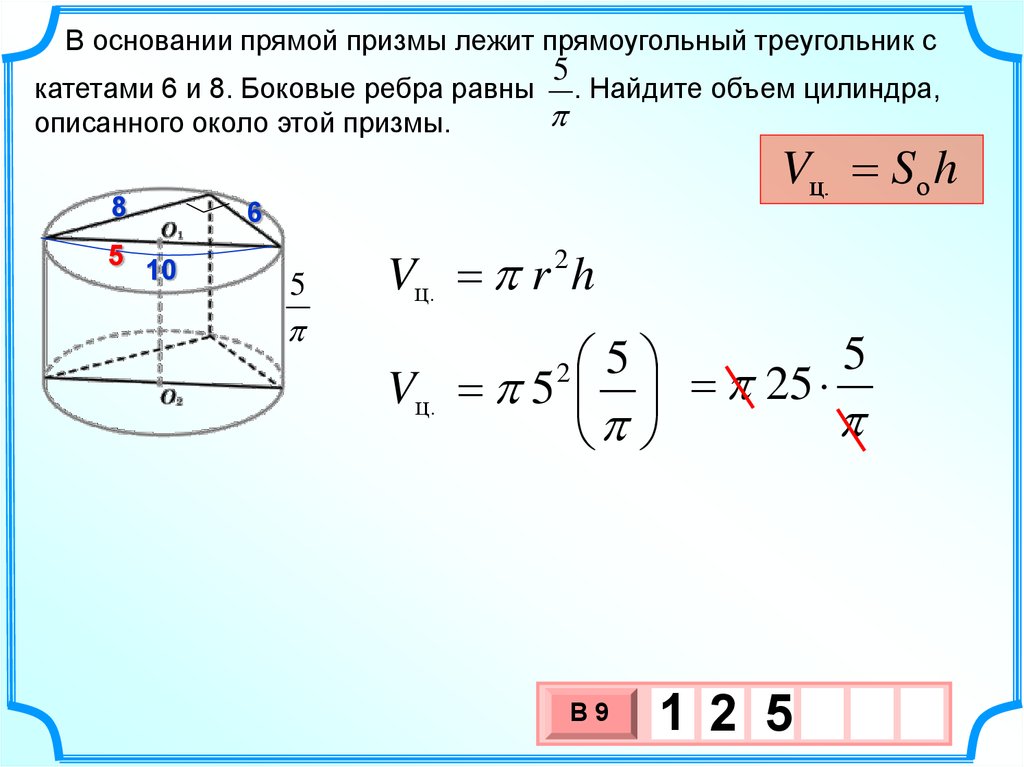
В основании прямой призмы лежит прямоугольный треугольник с
катетами 6 и 8. Боковые ребра равны
описанного около этой призмы.
8
5 10
5
. Найдите объем цилиндра,
Vц. Sо h
6
5
Vц. r h
2
5 25 5
Vц. 5
2
В9
1 2 5
3
10 х
х

7.

В основании прямой призмы лежит квадрат со стороной 2. Боковые
2
ребра равны . Найдите объем цилиндра, описанного около этой
призмы.
d 2 22 22
d2 8
2
2
2
2
d
2
d 8
d 2 2
Vц. Sо h
r 2
Vц. r h
2
Vц.
2
2
В9
2
4
4
3
10 х
х

8.

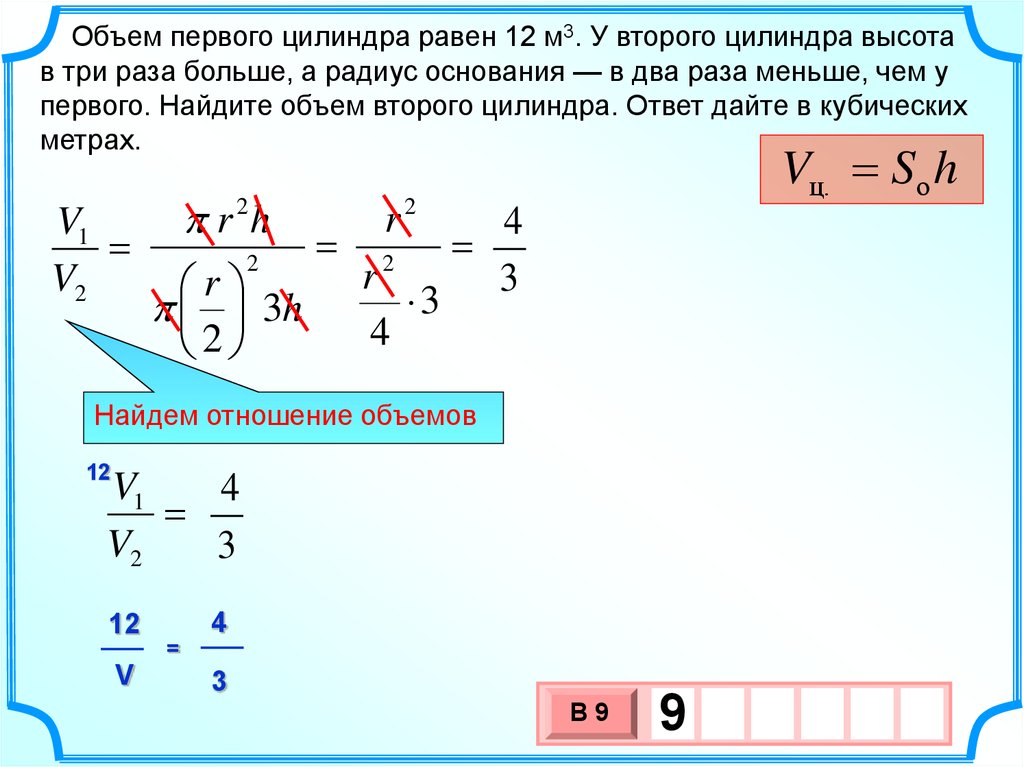
Объем первого цилиндра равен 12 м3. У второго цилиндра высота
в три раза больше, а радиус основания — в два раза меньше, чем у
первого. Найдите объем второго цилиндра. Ответ дайте в кубических
метрах.
V1
V2
r 2h
2
r
3h
2
r2
r2
3
4
Vц. Sо h
4
3
Найдем отношение объемов
12
V1
4
V2
3
4
12
=
V
3
В9
9
3
10 х
х

9.

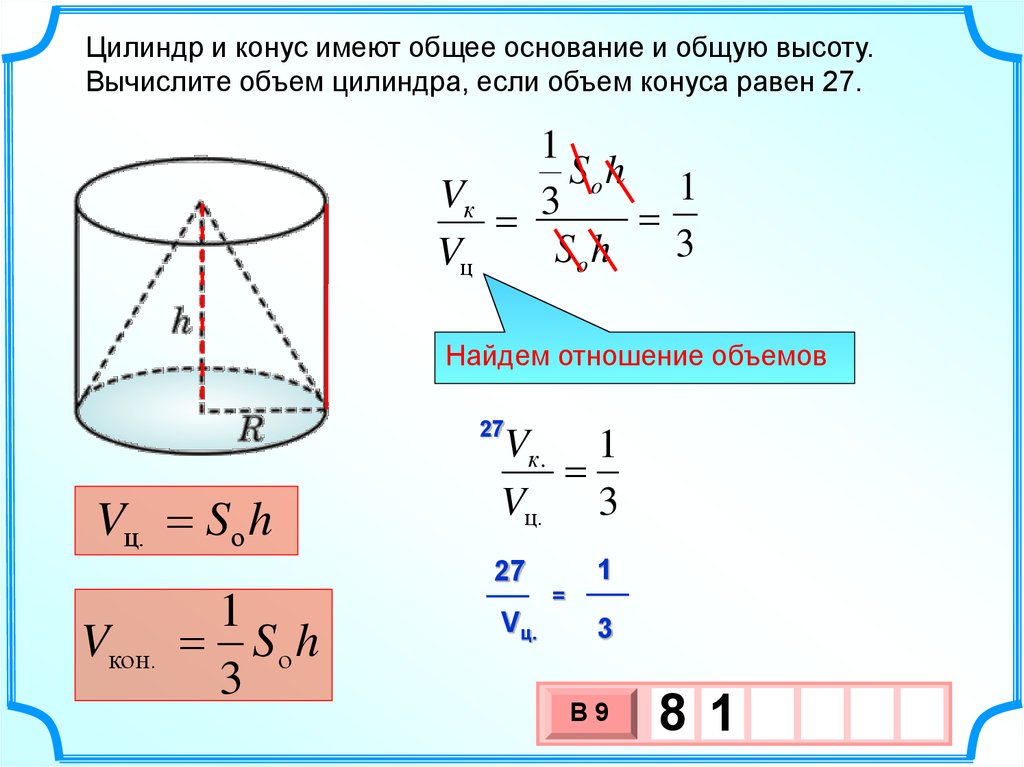
Цилиндр и конус имеют общее основание и общую высоту.
Вычислите объем цилиндра, если объем конуса равен 27.
1
So h 1
Vк
3
3
So h
Vц
Найдем отношение объемов
27
Vц. Sо h
Vк. 1
Vц. 3
1
27
Vкон.
1
Sо h
3
=
Vц.
3
В9
8 1
3
10 х
х

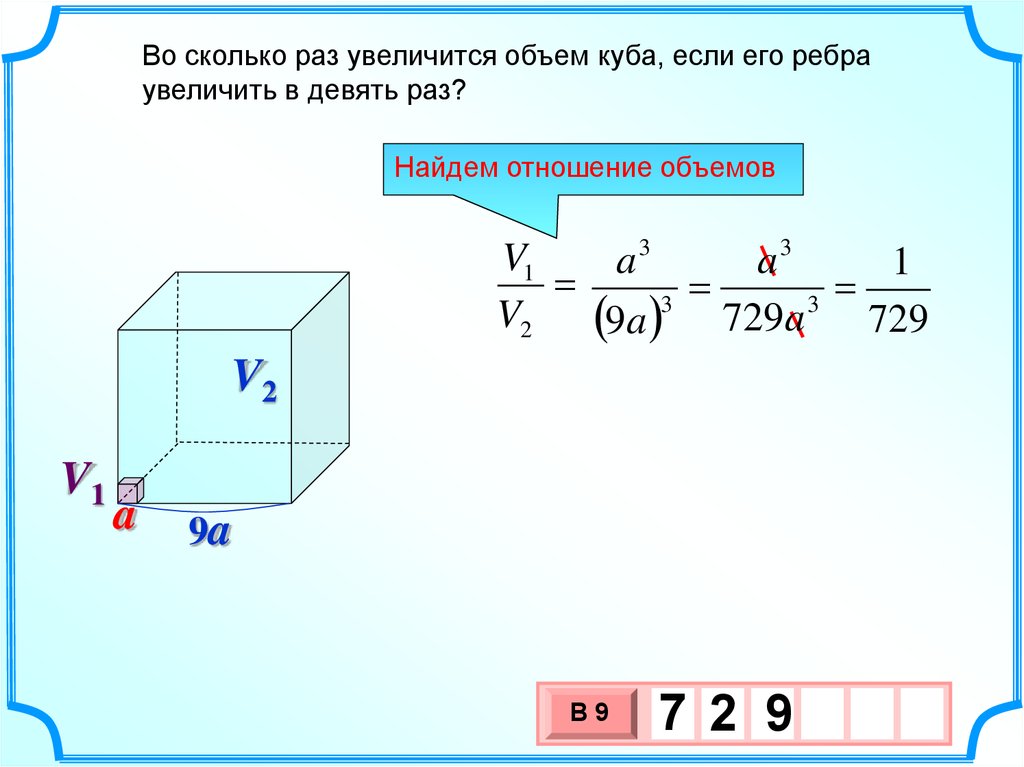
10.

Во сколько раз увеличится объем куба, если его ребра
увеличить в девять раз?
Найдем отношение объемов
3
3
V1
a
a
1
3
3
V2
9a 729a 729
V2
V1
a
9a
В9
7 2 9
3
10 х
х

11.

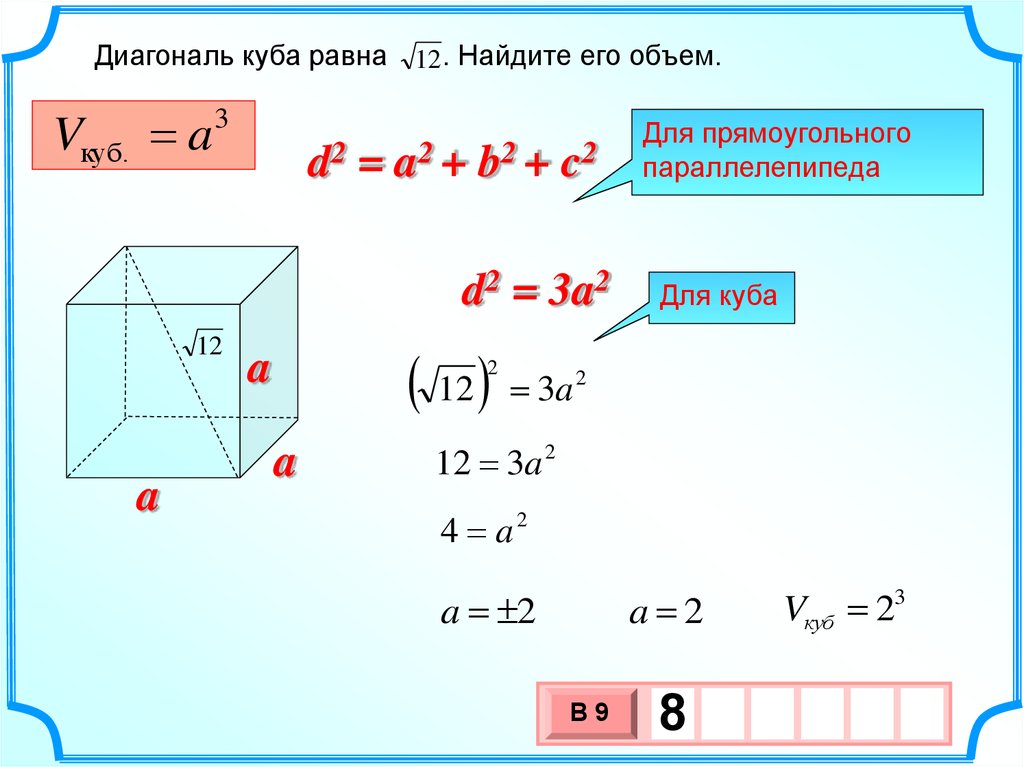
Диагональ куба равна 12 . Найдите его объем.
Vкуб. a
3
d2
=
a2 +
b2 +
c2
d2 = 3a2
12
a
12
a
2
a
Для прямоугольного
параллелепипеда
Для куба
3a 2
12 3a 2
4 a2
a 2
a 2
В9
8
Vкуб 23
3
10 х
х

12.

Объем куба равен 24 3. Найдите его диагональ.
d2 = a2 + b 2 + c2
Vкуб. a
a
a
d2 = 3a2
3
8 3
a
2
3
Для прямоугольного
параллелепипеда
24 3 a 3
d 32 3
3
2 3 a
d 2 3 4 3
2
2
3
Для куба
2
d 3 4 3
3
a 2 3
В9
d 3 2
6
3
10 х
х

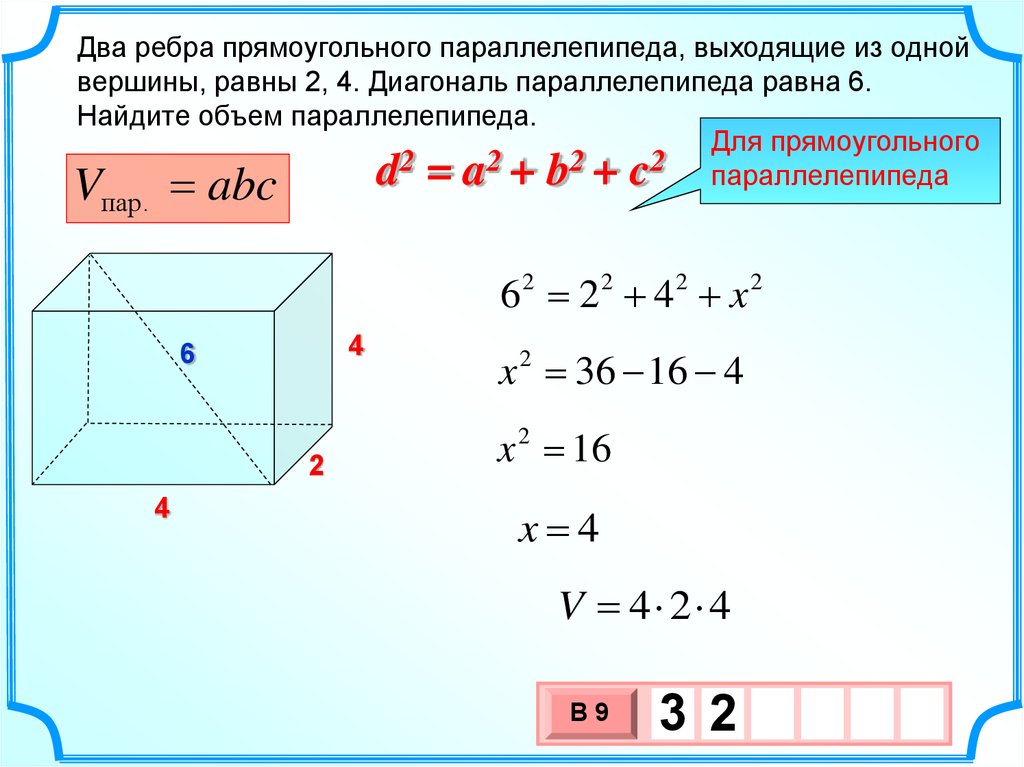
13.

Два ребра прямоугольного параллелепипеда, выходящие из одной
вершины, равны 2, 4. Диагональ параллелепипеда равна 6.
Найдите объем параллелепипеда.
Для прямоугольного
d2 = a2 + b2 + c2 параллелепипеда
пар.
abc
V
6 2 4 x
2
x4
6
2
2
2
x 2 36 16 4
x 16
2
2
4
x 4
V 4 2 4
В9
3 2
3
10 х
х

14.

Если каждое ребро куба увеличить на 1, то его объем увеличится
на 19. Найдите ребро куба.
Объем куба увеличится на 19.
Составим и решим уравнение:
(х+1)3 = х3 + 19
a
1 куб
Исходный куб
2 куб
Новый куб
ребро
x
х+1
V
x3
(x+1)3
В9
2
3
10 х
х

15.

B
a
1
2
S = ab sina
C
A
b
B
C
S = ab sina
a
A
A
D
b
a
параллелограмм
B
ромб
C
a
D
S=
2
a sina

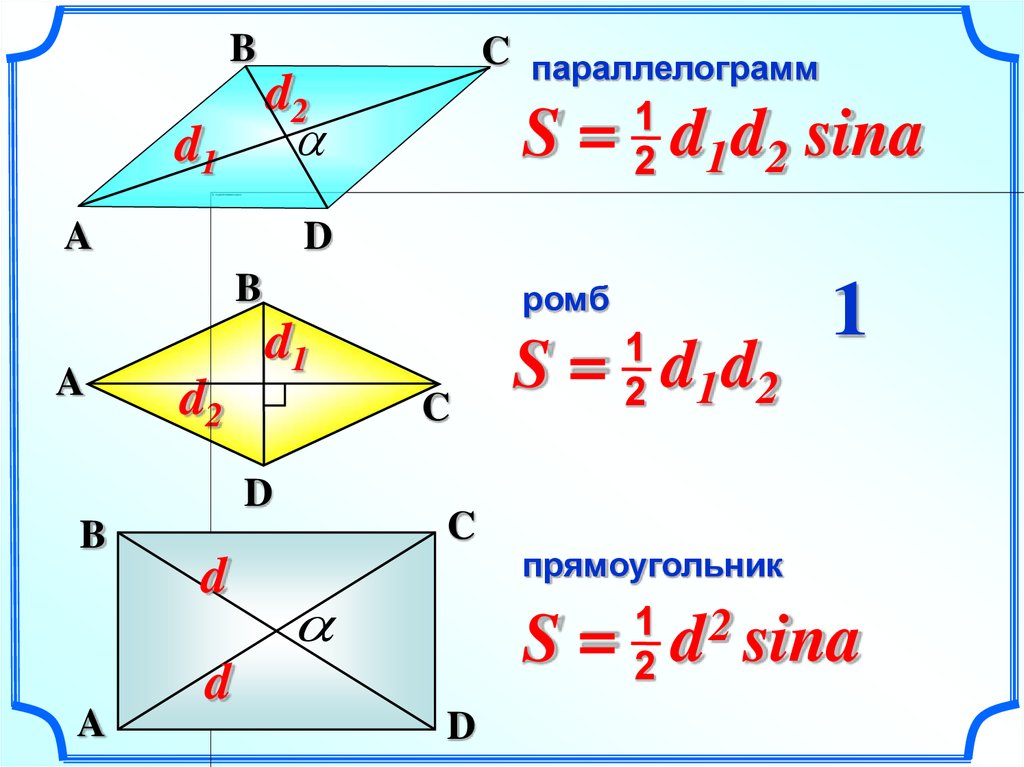
16.

B
C параллелограмм
1
2 1 2
d2
d1
A
S = d d sina
D
B
A
ромб
d1
d2
C
D
C
B
d
A
1
2
S = d1 d2 sin900
прямоугольник
S=
d
D
1
1
2
2
d sina

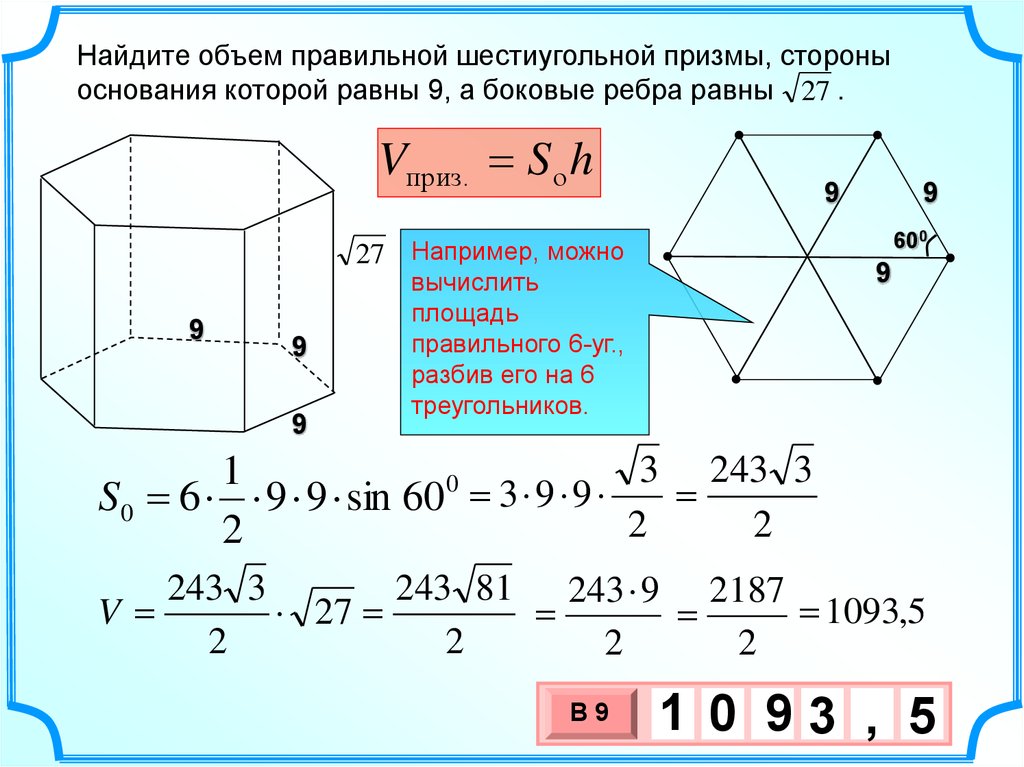
17.

Найдите объем правильной шестиугольной призмы, стороны
основания которой равны 9, а боковые ребра равны 27 .
Vприз. S о h
27
9
9
9
9
9
600
Например, можно
вычислить
площадь
правильного 6-уг.,
разбив его на 6
треугольников.
9
3 243 3
1
0
S0 6 9 9 sin 60 3 9 9
2
2
2
243 3
243 81 243 9 2187
1093,5
V
27
2
2
2
2
В9
1 0 93 , 5
3
10 х
х

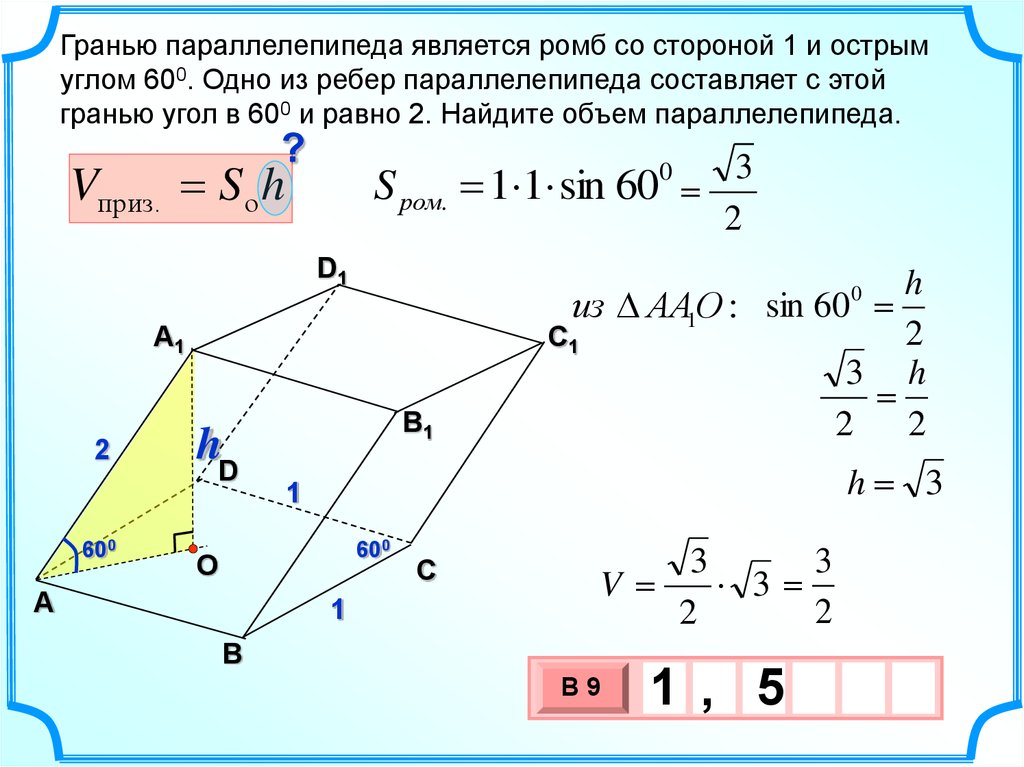
18.

Гранью параллелепипеда является ромб со стороной 1 и острым
углом 600. Одно из ребер параллелепипеда составляет с этой
гранью угол в 600 и равно 2. Найдите объем параллелепипеда.
?
Vприз. S о h
S ром.
D1
600
hD
B1
h 3
1
600
O
A
h
из АА1О : sin 60
2
C1
3 h
2
2
0
A1
2
3
1 1 sin 60
2
0
1
C
3
3
V
3
2
2
B
В9
1 , 5
3
10 х
х

19.

Через среднюю линию основания треугольной призмы, объем
которой равен 32, проведена плоскость, параллельная боковому
ребру. Найдите объем отсеченной треугольной
призмы.
1
S =
Обе призмы имеют
одинаковую высоту
2
ab sin a
1
a a sin h
2
V1
S1 h
1
1
V2
S2h
2a 2a sin h 4
2
Найдем отношение объемов
V1
1
V2
4
h
V1
32
a
2a
V2
В9
8
3
10 х
х

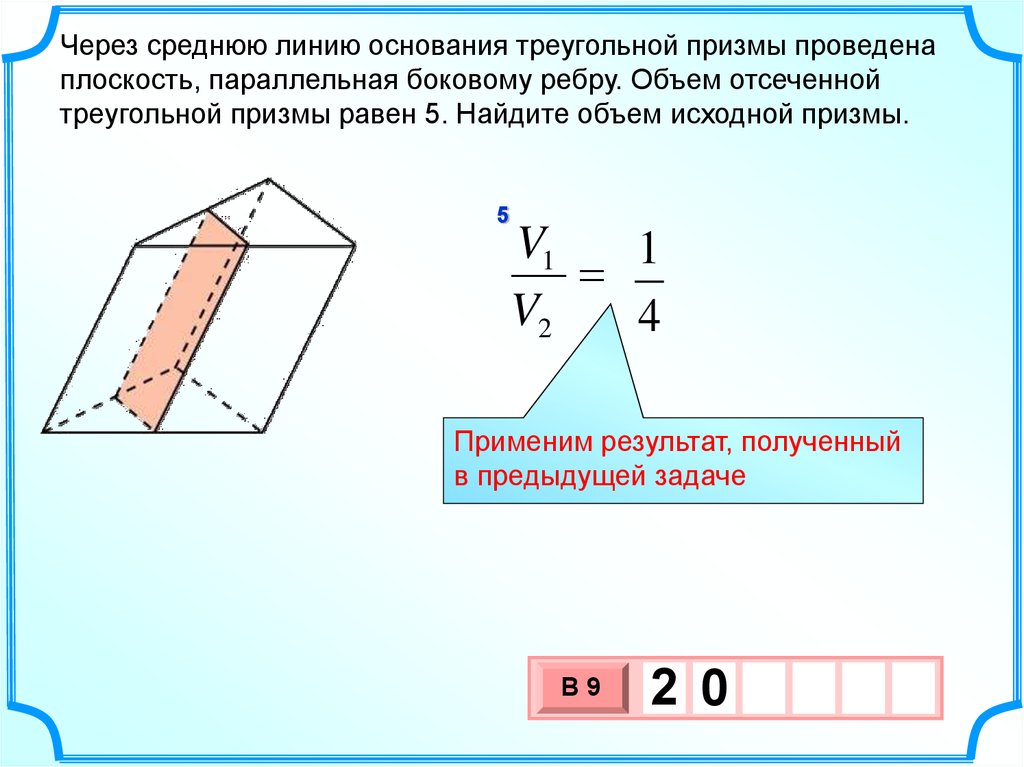
20.

Через среднюю линию основания треугольной призмы проведена
плоскость, параллельная боковому ребру. Объем отсеченной
треугольной призмы равен 5. Найдите объем исходной призмы.
5
V1
1
V2
4
Применим результат, полученный
в предыдущей задаче
В9
2 0
3
10 х
х

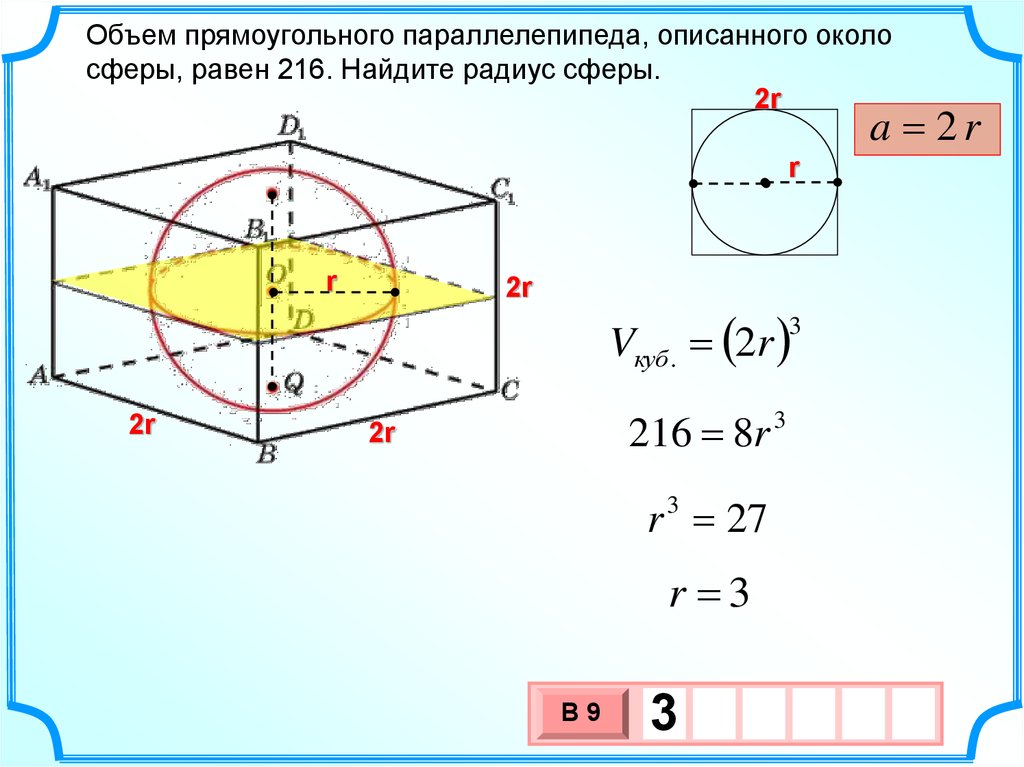
21.

Объем прямоугольного параллелепипеда, описанного около
сферы, равен 216. Найдите радиус сферы.
2r
a 2r
r
r
2r
Vкуб . 2r
3
2r
216 8r 3
2r
r 3 27
r 3
В9
3
3
10 х
х

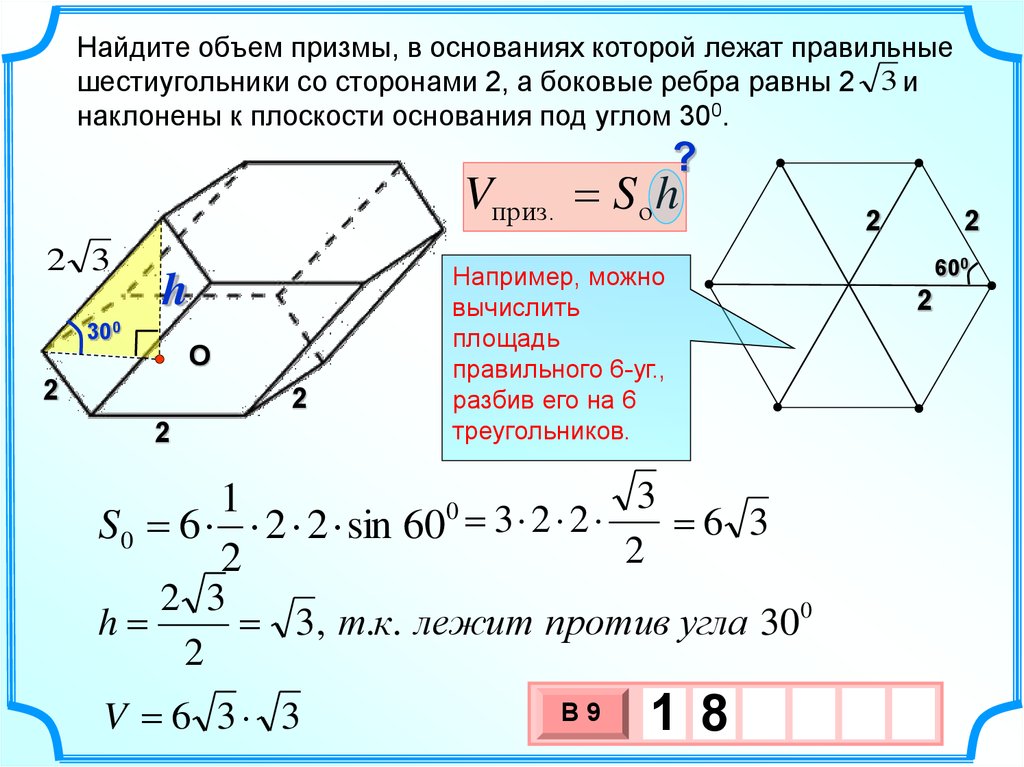
22.

Найдите объем призмы, в основаниях которой лежат правильные
шестиугольники со сторонами 2, а боковые ребра равны 2 3 и
наклонены к плоскости основания под углом 300.
?
Vприз. S о h
2 3
h
300
O
2
2
2
2
600
Например, можно
вычислить
площадь
правильного 6-уг.,
разбив его на 6
треугольников.
2
3
1
0
6 3
S0 6 2 2 sin 60 3 2 2
2
2
2 3
h
3 , т.к. лежит против угла 300
2
V 6 3 3
В9
1 8
2
3
10 х
х

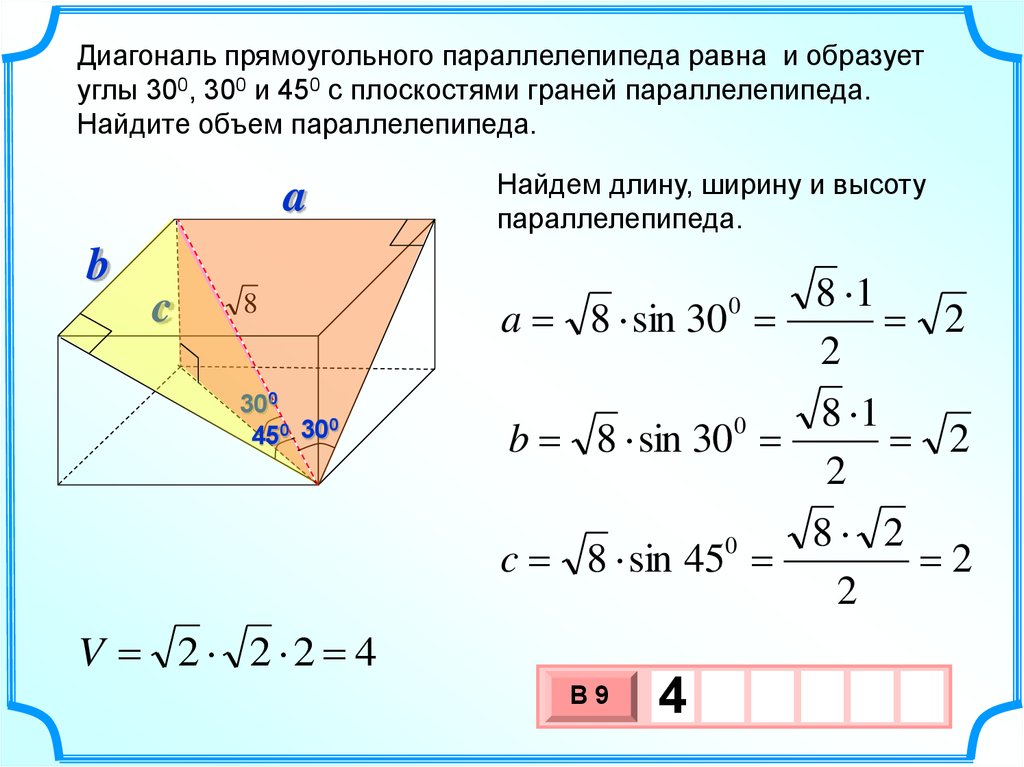
23.

Диагональ прямоугольного параллелепипеда равна и образует
углы 300, 300 и 450 с плоскостями граней параллелепипеда.
Найдите объем параллелепипеда.
a
b
c
8
300
0
450 30
Найдем длину, ширину и высоту
параллелепипеда.
8 1
a 8 sin 30
2
2
0
8 1
b 8 sin 30
2
2
0
8 2
c 8 sin 45
2
2
0
V 2 2 2 4
В9
4
3
10 х
х

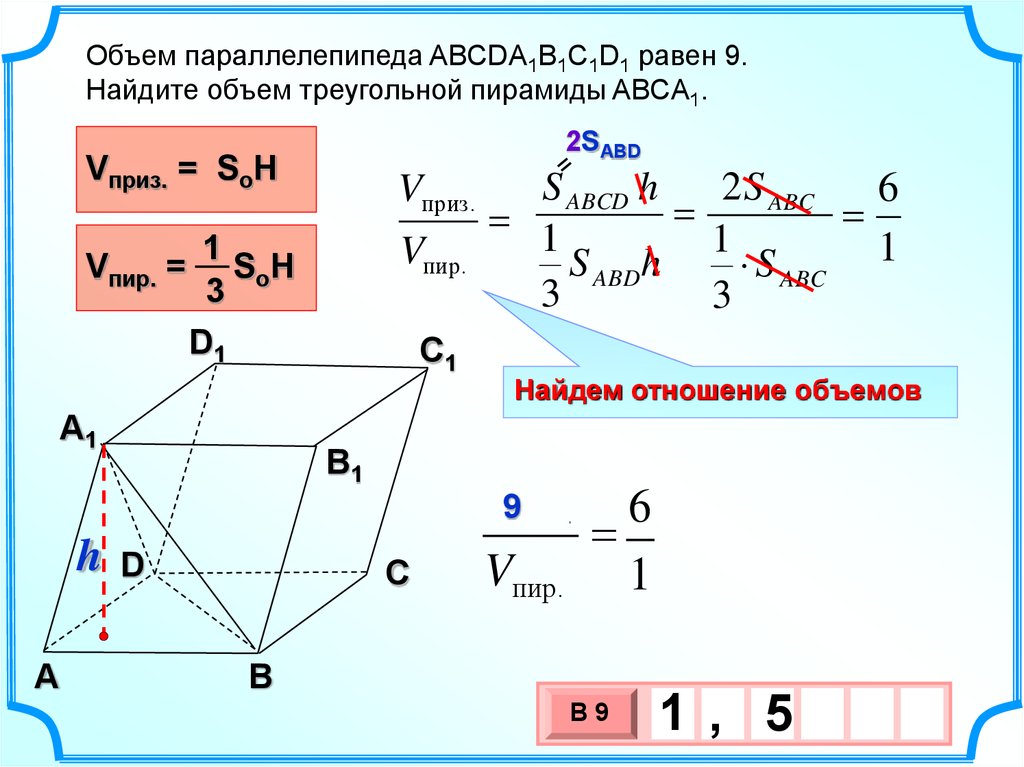
24.

Объем параллелепипеда ABCDA1B1C1D1 равен 9.
Найдите объем треугольной пирамиды ABCA1.
2SABD
Vприз. = SoH
Vприз.
1
Vпир. = SoH
3
D1
A1
h
A
Vпир.
C1
B1
D
S ABCD h
2 S ABC
6
1
1
S ABDh
S ABC 1
3
3
Найдем отношение объемов
V9приз.
C
Vпир.
6
1
B
В9
1 , 5
3
10 х
х