Похожие презентации:
Основные типы опор и балок
1. Лекция 3
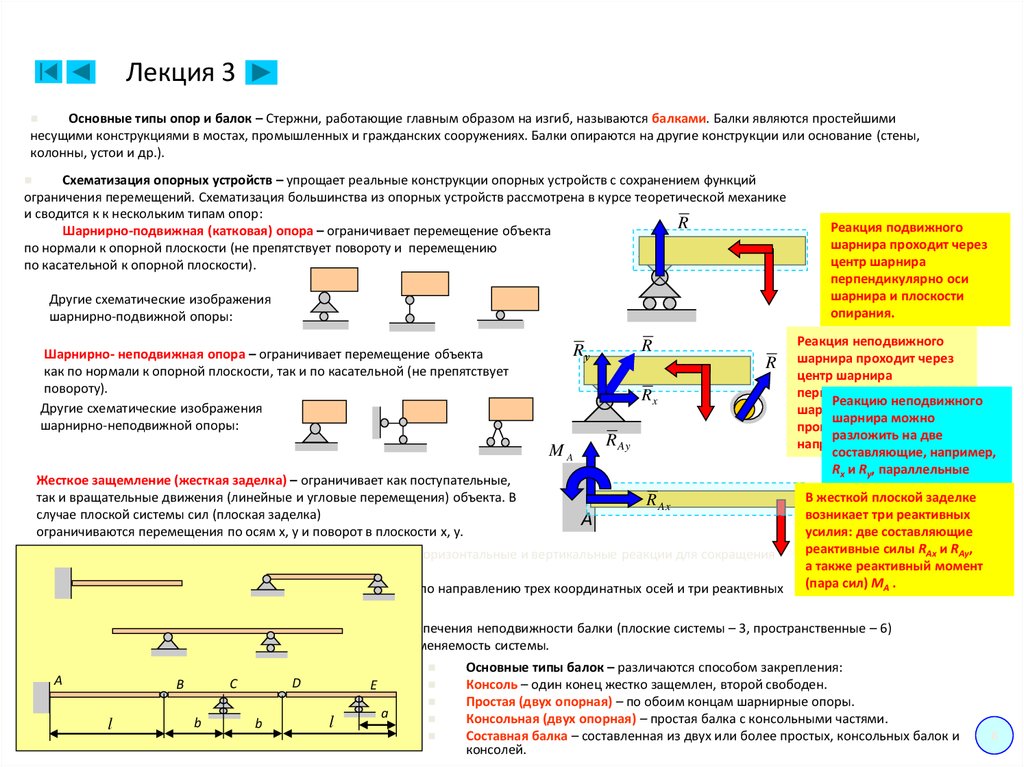
Основные типы опор и балок – Стержни, работающие главным образом на изгиб, называются балками. Балки являются простейшиминесущими конструкциями в мостах, промышленных и гражданских сооружениях. Балки опираются на другие конструкции или основание (стены,
колонны, устои и др.).
Схематизация опорных устройств – упрощает реальные конструкции опорных устройств с сохранением функций
ограничения перемещений. Схематизация большинства из опорных устройств рассмотрена в курсе теоретической механике
и сводится к к нескольким типам опор:
R
Шарнирно-подвижная (катковая) опора – ограничивает перемещение объекта
по нормали к опорной плоскости (не препятствует повороту и перемещению
по касательной к опорной плоскости).
Другие схематические изображения
шарнирно-подвижной опоры:
Реакция подвижного
шарнира проходит через
центр шарнира
перпендикулярно оси
шарнира и плоскости
опирания.
Реакция неподвижного
R шарнира проходит через
центр шарнира
перпендикулярно оси
Rx
Реакцию неподвижного
шарнира и имеет
шарнира можно
произвольное
разложить на две
R Ay
направление.
MA
составляющие, например,
Rx и Ry, параллельные
Жесткое защемление (жесткая заделка) – ограничивает как поступательные,
координатным осям.
В жесткой плоской заделке
так и вращательные движения (линейные и угловые перемещения) объекта. В
R Ax
возникает три реактивных
случае плоской системы сил (плоская заделка)
A
усилия: две составляющие
ограничиваются перемещения по осям x, у и поворот в плоскости x, у.
реактивные силы RAx и RAy,
В сопротивлении материалов и далее в строительной механике горизонтальные и вертикальные реакции для сокращения
а также реактивный момент
наименования часто обозначают как HA (horizontal) и VA (vertical).
(пара сил) MA .
В случае пространственной системы сил возникают три реакции по направлению трех координатных осей и три реактивных
момента (пар сил) относительно этих осей.
Шарнирно- неподвижная опора – ограничивает перемещение объекта
как по нормали к опорной плоскости, так и по касательной (не препятствует
повороту).
Другие схематические изображения
шарнирно-неподвижной опоры:
Rу
R
Во всех случаях число связей должно быть достаточным для обеспечения неподвижности балки (плоские системы – 3, пространственные – 6)
и способы постановки связей должны исключать мгновенную изменяемость системы.
Примеры мгновенно-изменяемых систем:
Основные типы балок – различаются способом закрепления:
A
D
C
Консоль – один конец жестко защемлен, второй свободен.
B
E
Простая (двух опорная) – по обоим концам шарнирные опоры.
a
Консольная (двух опорная) – простая балка с консольными частями.
l
b
b
l
Составная балка – составленная из двух или более простых, консольных балок и
консолей.
8
2. Лекция 3 (продолжение – 3.2)
Определение опорных реакций в балках – выполняется методами теоретической механики.Уравнения равновесия могут быть составлены в виде одной из трех форм:
X i 0;
Yi 0;
M iA 0
X i 0; x
M iB 0;
M iA 0 AB
M iC 0; C
M iB 0;
M iA 0 AB
Поскольку найденные опорные реакции участвуют в дальнейших расчетах (построение эпюр внутренних усилий, определение
напряжений и перемещений) следует активно пользоваться этими формами уравнений так, чтобы в каждое из уравнений входила лишь одна
определяемая реакция, чтобы исключить подстановку ранее найденных и не проверенных реакций. После независимого вычисления всех
реакций обязательно должна быть сделана проверка составлением такого уравнения равновесия, в котором бы присутствовали все или
большинство из найденных реакций. Поскольку балки несут преимущественно вертикальную нагрузку, то в общем случае рекомендуется
воспользоваться формой II и проверить вертикальные реакции составлением уравнения в проекциях на вертикальную ось.
Помните, что неверно найденные реакции в любом случае приведут к неверным результатам при построении эпюр, определении
напряжений и перемещений!
Внутренние усилия при изгибе – При изгибе возникают в общем случае изгибающие моменты Mx, My и поперечные силы Qx , Qy.
Если в поперечном сечении возникает только один изгибающий момент Mx, то такой изгиб называется чистым.
Mx
+
В большинстве случаев дополнительно к изгибающему моменту возникает поперечная сила Qy, и такой изгиб
называется поперечным.
Если внешняя нагрузка и реактивные усилия лежат в одной плоскости, то такой изгиб называется плоским.
Правила знаков для изгибающего момента – Изгибающий момент принимается положительным,
Mx
если он изгибает элемент балки так, нижние волокна оказываются растянутыми, т.е. ось балки искривляется
+
Qy
выпуклостью вниз.
Правила знаков для поперечной силы – Поперечная
сила
считается
положительной,
если
она
С использованием этих основных зависимостей получаем:
стремится повернуть элемент балки по ходу часовой стрелки.
d 2M x
■ Дифференциальные зависимости при изгибе – связывают внутренние усилия между
в сечении и нагрузкой.
qсобой
y.
2
Выделим из балки элемент длиной dz, находящийся по действием внешней вертикальной
равномерно распределенной
dz
y
Qy
нагрузкой q, и заменим действие отброшенных частей внутренними усилиями:
Вторая производная от изгибающего момента
Выделенный элемент находится в равновесии
Mx Qy
Q y q y dz равна
(Q y dQ y ) 0;
Yi 0; координате
по продольной
и удовлетворяет уравнения равновесия:
dz
интенсивности
O
M 0i 0; - распределенной
M x q y dz нагрузки.
(Q y dQ y )dz ( M x dM x ) 0.
Из первого уравнения
получаем:
dQ y
dz
q y .
Производная от поперечной силы
по продольной координате равна
интенсивности распределенной нагрузки.
2
Из второго уравнения, пренебрегая малыми
второго порядка получаем:
Производная от изгибающего момента
по продольной координате равна поперечной силе.
dM x
Qy .
dz
Mx
Mx
Qy
Qy
qy
Mx+dMx
z
Qy+dQy
dz
9
3. Лекция 3 (продолжение – 3.3)
Построение эпюр изгибающих моментов и поперечных сил – принципиально ничем не отличается от построения эпюры продольных сил и крутящихмоментов. Положительные значения поперечной силы Qy откладываются вверх от горизонтальной базовой линии, а отрицательные – вниз.
Положительные значения изгибающих моментов Mx откладываются вниз – со стороны растянутого волокна. Таким образом расположение ординат
эпюры Mx указывают, какие волокна растянуты.
Примечание: Это правило принято в строительных и транспортных вузах в то время, как в машиностроительных и авиационных вузах используется обратное правило
(положительный момент откладывается со стороны сжатого волокна).
Пусть балка нагружена равномерно распределенной нагрузкой q, сосредоточенной силой F=qa и крутящим моментом M=qa2:
y z1 I
II
1. Определяем
z2
III
z3
Z i 0; H A 0;
q
F
M
опорные реакции:
HA A
VB = 1,75qa
B
M Ai 0; F 6a M VB 4a (q 2a)a 0;
z
VA
I
II
III
VA = 1,25qa
M Bi 0; F 2a M (q 2a)3a V A 4a 0;
VB
2
2
2
2.
Количество
участков
–
3.
F
6
a
M
q
2
a
qa
6
a
qa
q
2
a
2a
2a
2a
VB
1,75qa.
Из второго
и третьего
3. Проведем
сечение
I-I на выражения
первом участке
и определим
текущую
координату
сеченияпостроим
и пределы
ее
Используя
полученные
для поперечной
силы
и изгибающего
момента
эпюру
4
a
4
a
y
2
2
2
уравнений
получаем:
изменения:
0
z
2a.
поперечных
сил
и
изгибающих
моментов,
подставляя
значения
реакций
и
координаты
начала
и конца
1
F 2a M q 6a
qa 2a qa q6a
I-I
V Aдействие
Q I-I имомент
1,25
q Mx
A
I-I .
участков. Вправую
случаечасть,
квадратичного
изменения
величины
(изгибающий
на
первом
участке)
4. Отбросим
заменим ее
поперечной
силой
изгибающим
моментом
Mqa
y
x
4
a
4
a
C
дополнительно
подставляется
внутри интервала,
посредине. через
и составим
уравнения
равновесиякоордината
в проекцияхточки
Выполняем
контроль:
Yi 0; VиAв моментах
q2a Vотносительно
F 0например,
; 1оси
,25x,
qaпроходящей
2qa 1,75qa qa 0.
VA
B
Откладывая
не
каждом
из
участков
значения
поперечных
сил
и
изгибающего
момента
центр
текущего
сечения
(т.е.
относительно
точки
С)
:
I-I
Qy
z
I
в некотором выбранном
масштабе
MxM
:
q
Yi
0; V A получаем
qz1 Q yIэпюры
0Q; y и
0; V A z1 qz1 1 M xI I 0.
MxII-II
Ci
Полученные
выражения
показывают,
что:
A
2
Отсюда получаем:
поперечная сила в сеченииDравна
I I
2
QyIII-III F
Q
V
qz
.
z
y
A
1
I
I
1
алгебраической
сумме проекций
VA
M x V A z1 q .
на вертикальную ось внешних
QyII-IIсил,
2
Повторяем шаги 3 и 4 для следующих участков:
взятых по одну сторону от сечения, E
изгибающий момент - алгебраической
MxIII-III
сумме 3. Проведем сечение II-II на втором участке и определим текущую координату сечения и пределы ее
моментов относительно горизонтальной оси, изменения: 0 z2 2a.
Свойства эпюр:
проходящей через центр тяжести сечения,
4. Отбросим правую часть, заменим ее действие поперечной силой QyII-II и изгибающим моментом MxII-II
1.внешних
Равномерно
распределенная
нагрузка
сил взятых
по одну сторону
от на участке
своего
действия вызывает на эпюре Q наклонную и составим уравнения равновесия в проекциях и в моментах относительно оси x, проходящей через
сечения!
центр текущего сечения (т.е. относительно точки D) :
прямую линию, падающую
в сторону
действия нагрузки,
прав
лев
Q yM –
Fyi с
Fyi .
а на эпюре
параболу
выпуклостью
в ту же сторону.
Yi 0; V A q2a Q yII II 0; M Di 0; V A (2a z 2 ) q2a a z 2 M xII II 0.
2. Сосредоточенная сила вызывает на эпюре Q
Отсюда получаем:
прав
лев
Q yII II V A q2a.
скачок вM
точке
приложения
силы
в
сторону
действия
силы,
M xII II VA (2a z 2 ) q2a(a z 2 ).
M
M
.
x
xi
xi
а на эпюре М – перелом в ту же сторону.
получаем для участка 3 (0 z3 2a):
слагаемых положителен,
3.Знак
Сосредоточенный
момент не если
вызывает на эпюреАналогично
Q
рассматриваемый фактор, будучи
Yi 0; Q yIII III F 0; M Ei 0; M xIII III F (2a z3 ) 0.
в приложен
точке его приложения
никаких
особенностей,
к поперечному
сечению
другой
а части,
на эпюре
M вызываетположительному
скачок в ту же сторону.
соответствует
Q yIII III F .
M xIII III F (2a z 2 ).
Смотрите
и удивляйтесь!
направлению
определяемого внутреннего
10
усилия.
4. Лекция 4
Центральное растяжение-сжатие – Во многих элементах конструкций возникают только продольные усилия, вызывающие в них деформациирастяжения или сжатия (стойки, элементы ферм, тяги, тросы и т.п.). При этом в местах приложения условно сосредоточенных сил характер
распределения деформаций достаточно сложный и отличается от распределения деформаций на удалении от этой локальной области. Размер этой
области равен примерно наибольшему из размеров поперечного сечения.
Принцип Сен-Венана - Если совокупность некоторых сил, приложенных к небольшой части поверхности тела, заменить статически эквивалентной
системой других сил, то такая замена не вызовет существенных изменений в условиях нагружения частей тела, достаточно удаленных от мест
приложения исходной системы сил.
Как показывает опыт, за пределами этой области деформации практически постоянны и поперечные сечения перемещаются параллельно своим
начальным положениям. На основании этого вводится гипотеза плоских сечений (Я. Бернулли):
Поперечные сечения стержня, плоские и перпендикулярные оси стержня до деформации, остаются плоскими и перпендикулярными
после деформации.
Напряжения и деформации – Как было ранее сказано, задача определения напряжений всегда является статически неопределимой.
Такие задачи решаются последовательным рассмотрением статической, геометрической и физической сторон.
В данном случае имеем статическое уравнение, связывающее внутреннее усилие – продольную силу с напряжением:.
N
z dA;
A
Для вычисления интеграла необходимо знать закон изменения напряжений по сечению. Этот закон можно установить
изучением непосредственно наблюдаемых перемещений (деформаций). Поскольку принимается гипотеза плоских сечений, то при отсутствии
внешней распределенной продольной нагрузки деформации постоянны по сечению и по длине стержня (геометрия) . Из введенного ранее
определения деформаций в точке :
dz
l
z
const .
прод z , где l – абсолютная продольная деформация
dz
l
(удлинение), l - длина (базовая длина) стержня.
Опытным путем установлена фундаментальная (физическая) связь усилий и удлинений (Р. Гук) и в дальнейшем, напряжений и деформаций (Коши, Навье) в
виде:
E , где Е – модуль упругости (физическая постоянная материала, определяемая экспериментально).
Подстановка последнего соотношения – закона Гука в интегральное выражение c учетом постоянства деформации и напряжения дает:
N z dA z A;
A
z
N
.
A
Нормальное напряжение в поперечном сечении прямо пропорционально величине
продольного усилия и обратно пропорционально площади сечения.
Абсолютную деформацию (удлинение) стержня также можно определить через продольное усилие:
l z l
Формула для абсолютного удлинения справедлива лишь при постоянной по длине стержня продольной силе
и неизменной площади поперечного сечения! В случае переменной продольной силы, например, при учете собственного
веса вертикальных стержней, и/или переменной площади необходимо использовать интегральное выражение:
E
l
l.
Nl
.
EA
l
Ndz
.
0 EA
l
11
5.
6.
7. Лекция 4 (продолжение – 4.2)
Коэффициент Пуассона – При растяжении стержня наряду с продольной деформацией (удлинением), определяемой законом Гука,возникает поперечная деформация (сужение поперечного сечения), выражающаяся в уменьшении поперечных размеров стержня.
Относительные поперечные деформации вычисляются как
где b, h – размеры поперечного
h
b
сечения.
попер x , попер y ,
h
b
Экспериментально установлено, что имеется линейная связь
между продольной и поперечной деформацией:
попер
прод
где μ – коэффициент
пропорциональности, называемый
коэффициентом Пуассона.
Коэффициент Пуассона для данного материала в пределах упругих деформаций имеет постоянное значение
Материал
и находится в пределах от 0 до 0,5.
По закону Гука, определяющему связь нормальных напряжений с продольными деформациями:
Тогда
x y z
z
E
z
.
Как упоминалось ранее, в общем случае нагружения по граням выделенного
элемента возникают нормальные и касательные напряжения. Последние,
вызывая деформации сдвига, не влияют на линейные деформации,
поскольку не изменяют длин сторон элемента. Используя принцип независимости
действия сил, справедливый
для изотропного и линейно упругого материала,
можно записать обобщенный закон Гука, учитывающий одновременное действие
нормальных напряжений по всем граням элемента:
z
E
.
1
[ x ( y z )];
E
1
y [ y ( z x )];
E
1
z [ z ( x y )].
E
x
Напряжения по наклонным площадкам – При растяжении стержня в его
поперечном сечении возникают только нормальные напряжения. Посмотрим
какие напряжения возникают в сечении, не перпендикулярном оси стержня.
Сталь
0,25-0,33
Медь, бронза
0,31-0,35
Чугун
0,23-0,27
Бетон
0,08-0, 18
Древесина
вдоль волокон
поперек волокон
0,5
0,02
Алюминий
0,32-0,36
Резина, каучук
0,47-0,5
N
1. Отбросим правую часть и заменим ее действие главным вектором внутренних сил R :
Анализ
полученных
соотношений
показывает:
Из уравнения
равновесия
в проекции
на ось стержня R = F.
1. При = 0 (наклонная площадка совпадает с поперечным сечением):
z ; 0.
2.Касательные
Разложим это
внутреннееотсутствуют,
усилие на нормальную
и касательную
напряжения
а нормальные
напряжения к сечению составляющие N и Q :
3.максимальны.
Вычислим нормальные и
N F cos F
Q
F sin F
2.касательные
При = 45о касательные
максимальны,
cos 2 ;
sin cos .
напряжения напряжения
A
A
A
A
апо
нормальные
напряжения
z ;A Az .
наклонному
сечению равны касательным.
F
R
F
Q
N R cos F cos ;
Q R sin F sin .
cos
cos
площадью A =A/cos :
3.Здесь
При по-прежнему
= 90о (продольная
площадка)
нормальные
и
касательные
напряжения
обращаются
предполагается равномерное
С учетом того, продольная сила N в поперечном сечении равна внешней
в распределение
ноль (продольные
волокна
давят друг на друга и не сдвигаются).
напряжений
поне
сечению.
растягивающей силе F, отношение F/A = N/A есть нормальное напряжение
4. На двух взаимно перпендикулярных площадках касательные напряжения
в поперечном сечении. Тогда получаем:
равны по абсолютной величине.
2
μ
2
cos 2 ;
1
2
sin 2 .
12




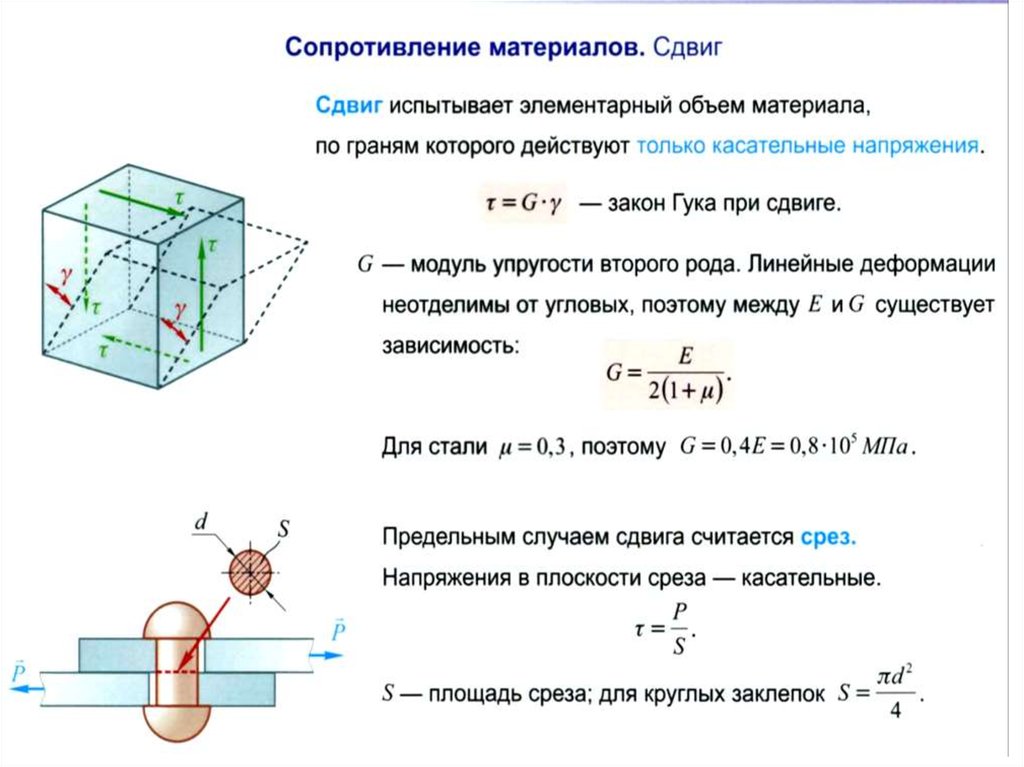

 Механика
Механика








