Распределение «хи-квадрат»

1. 6.5. Распределение «хи-квадрат»

6.5. Распределение «хиквадрат»
Пусть Xi (i=1,…,n) – система независимых
нормированных нормально
распределенных СВ с МО, равным 0, и
единичной дисперсий. Тогда СВ 2 ,
представляющая собой сумму квадратов
этих величин,
n
2
2
= Xi
i 1
распределена по закону “хи-квадрат” с k=n
степенями свободы.

2.

Если на величины Xi (i=1,…,n) наложено r
связей, то число степеней свободы k=n-r.
Плотность этого распределения определяется: 0 2 ,
1
2
p( )
2
где
k /2
Г ( k / 2)
2 ( k / 2) 1
2
( )
exp( / 2)
x 1
Г( x ) t
exp( t )dt
0
-
гамма-функция (интеграл Эйлера второго
рода). В частности Г(n+1)=n!.

3.

Из определения плотности вероятности
распределения 2 следует, что
распределение “хи-квадрат”
определяется одним параметром –
числом степеней свободы k. С
увеличением числа степеней свободы
распределение “хи-квадрат” медленно
приближается к нормальному.

4.

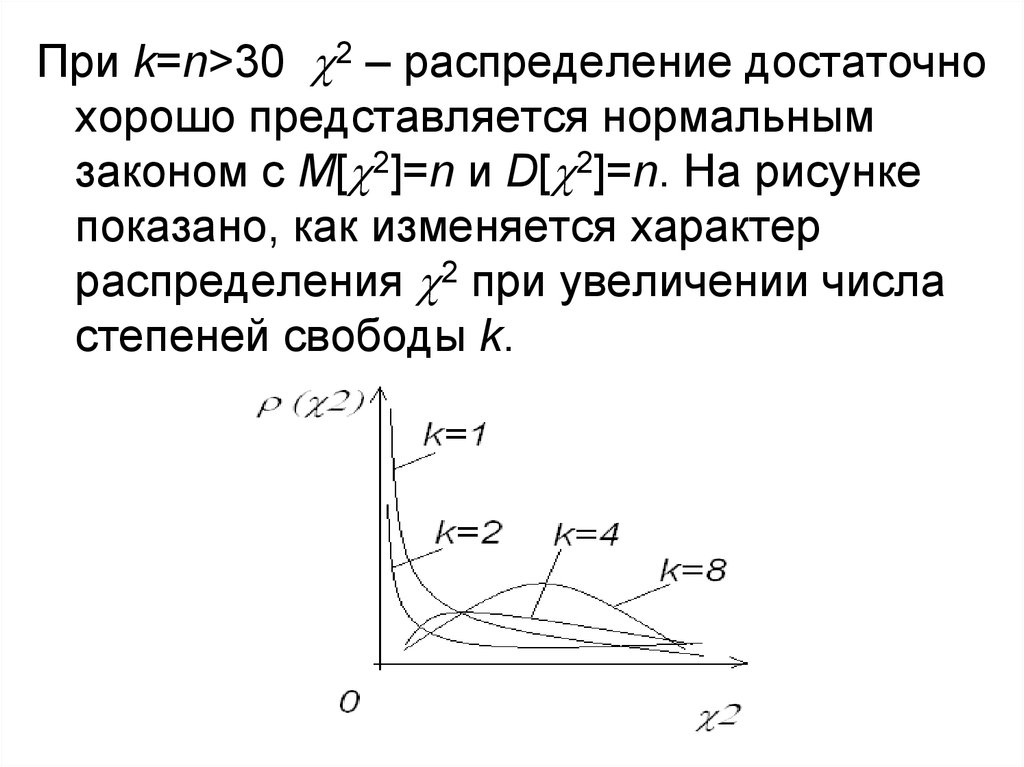
При k=n>30 2 – распределение достаточно
хорошо представляется нормальным
законом с M[ 2]=n и D[ 2]=n. На рисунке
показано, как изменяется характер
распределения 2 при увеличении числа
степеней свободы k.

5. 6.6. Распределение Стьюдента

Пусть случайные величины Z, X1, X2, …, Xn
подчинены нормальному закону
распределения с нулевым средним и
произвольной дисперсией. Пусть далее
величина Z не зависит от Xi, i = 1, …, n, и
среди Xi имеется ровно k линейно
независимых величин.

6.

Тогда случайная величина
t
Z
1 n
2
Xi
k i 1
имеет распределение Стьюдента (tраспределение), с плотностью
распределения

7.

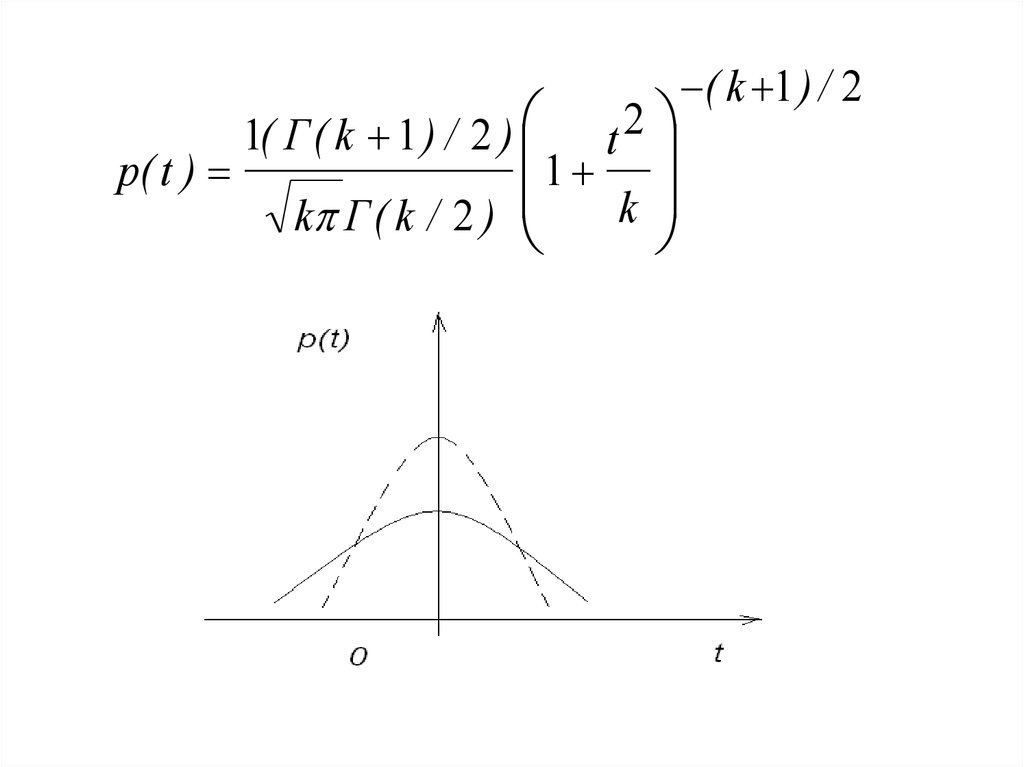
p( t )
1( Г ( k 1 ) / 2 )
k Г ( k / 2 )
1
2
t
k
( k 1 ) / 2

8.

Заметим, что t-распределение не зависит от
2. Величина t, определенная для
нормированных случайных величин с
нулевым средним и единичной
дисперсией, также распределена по закону
Стьюдента.
Распределение Стьюдента симметрично
относительно начала координат. С
возрастанием числа степеней свободы
быстро приближается к нормальному
закону распределения.

9.

Для нормированных СВ распределения
Стьюдента приближается к нормальному
закону с характеристиками M[t] = 0 и
D[t] = k / (k – 2).

10. 6.7. F-распределение Фишера

Если X и Y – независимые случайные
величины, распределенные по закону 2
со степенями свободы k1 и k2 , то
величина
имеет
FX / k1
распределение
F
Y / k2
Фишера со
степенями
свободы k1
и k 2.

11.

Плотность этого распределения определяется
выражением
k1 / 2 k 2 / 2
(k k )/ 2
k1 k 2 Г (( k1 k 2 ) / 2 ) ( k1 2 ) / 2
1
2
p( F )
F
(k k F )
2 1
Г ( k1 / 2 ) Г ( k 2 / 2 )

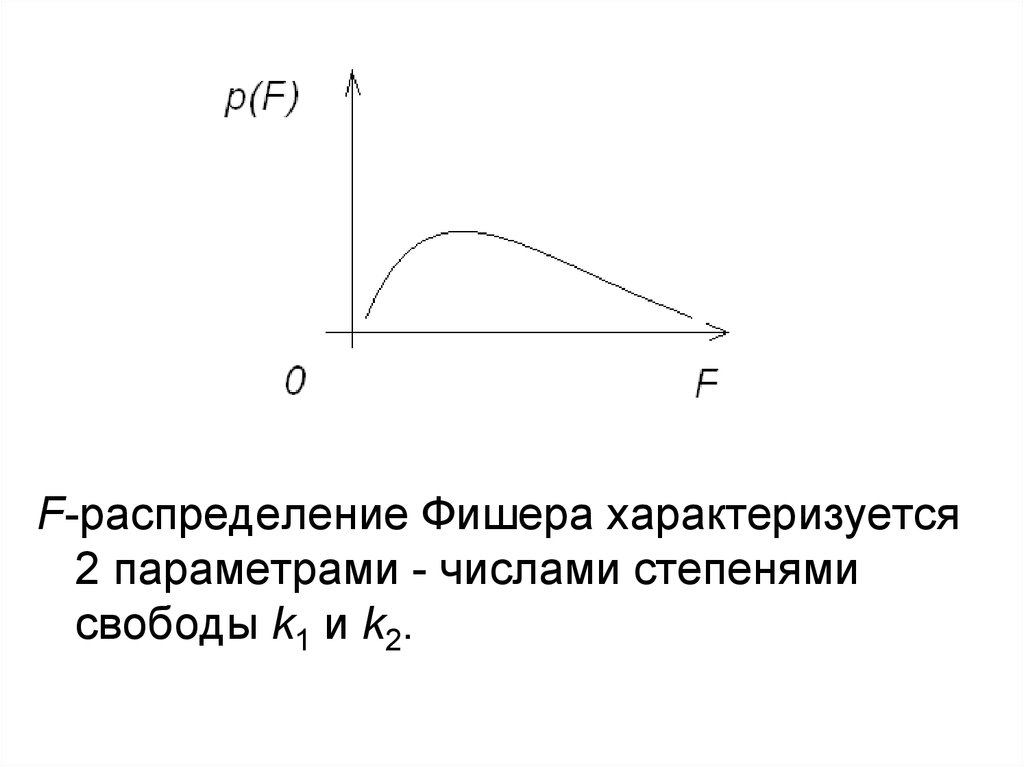
12.

F-распределение Фишера характеризуется
2 параметрами - числами степенями
свободы k1 и k2.

13. 6.8. Первичная обработка результатов измерений

Первичная
обработка
результатов
измерений состоит из последовательного
выполнения следующих шагов.

14.

1.Построение случайной выборки измерений
и простого статистического ряда.
2.Построение вариационного ряда
3.Грубые ошибки измерений. Исключение
грубых ошибок.
4.Оценка математического ожидания
случайной величины.
5.Оценка дисперсии случайной величины.
6.Оценка вероятности случайного события.
7.Оценка функции и плотности
распределения случайной величины.

15.

Рассмотрим более детально вопросы
исключения грубых ошибок и оценки
вероятности случайного события.
Получив выборку наблюдений случайной
величины Х с функцией распределения
F(x) следует убедиться, что она
действительно соответствует этой
функции распределения.

16.

Так как в процессе измерений
предполагаемая статистическая
обстановка может нарушиться и среди
реализаций xi могут появляться
ошибочные, т.е. не соответствующие
F(x) значения.
Обычно в качестве ошибочных
подразумевают xmin и xmax и их
называют грубыми ошибками, если
установлено их несоответствие закону
F(x).

17.

Если F(x) известно, то вопрос об ошибочности xmax может быть решен следующим
образом. Зная F(x), можно найти
F(n)(x) – функцию распределения
X(n) = Xmax.
Тогда задаваясь вероятностью 1
практически достоверного события,
из уравнения
P( X
t ) F (t )
max
(n)
можно найти границу t , правее которой

18.

появление реализации xmax в
соответствии с принципом практической
уверенности невозможно.
Отсюда следует решающее правило:
если xmax t , то xmax считают грубой
ошибкой, в противном случае xmax
считают согласующейся с законом
распределения F(x).
В случае независимых измерений
F( t ) n

19.

Аналогично решается вопрос об
ошибочности xmin . Здесь определяется
граница t из условия:
P( X
min
) F (t )
(1)
t
где =1- - вероятность практически
невозможного события.
Затем применяют решающее правило
принципа практической уверенности:

20.

xmin – грубая ошибка, если xmin < t ; xmin не
противоречит F(x) – в противном
случае.
При независимых измерениях t
находится из уравнения:
n
F( t ) 1 1
Чаще F(x) бывает неизвестной. Тогда для
решения поставленной задачи
применяют частные приемы.

21.

Например, если F(x) нормального закона
распределения с неизвестными
параметрами m = M[X] и 2 = D[X], то
строят вспомогательную случайную
X
X
величину
max
T
где
S
– оценка
среднеквадратического отклонения

22.

Затем устанавливают ее функцию
распределения FT(t) = P(T < t) далее
находят верхнюю границу t допустимых
значений Т из уравнения FT(t ) = = 1 – .
Верхней границей допустимых значений
xmax становится величина
x st

23.

В итоге получаем следующее частное
решающее правило: если
x max x st
то она считается соответствующей
нормальному распределению;
в противном случае величина xmax
считается грубой ошибкой.

24.

Анализ ошибочности xmin выполняется
аналогично по решающему правилу:
x min x st
то xmin считается соответствующей
нормальному закону; в противном случае
величину xmin считают грубой ошибкой.
Для определения границ t составлены
специальные таблицы, входом которых
служат n и =1- .

25.

Оценим вероятность Р(А)=р появления
события А в n опытах.
В качестве оценки рассмотрим частоту
событий:
p* = m*/n,
где m* - число опытов, в которых
наблюдалось событие А,
n – общее число опытов.

26.

Из т.Бернулли следует, что оценка
вероятности события р* является
состоятельной, является оценкой
сходящейся по вероятности к
оцениваемому параметру.
Определим математическое ожидание и
дисперсию оценки р*. Т.к. m* случайная величина, распределенная
по биномиальному закону с
математическим ожиданием
M[m*] = np и дисперсией D[m*] = npq, то

27.

M ( p*)
D( p*)
m*
M
n
m*
D
n
1
n
1
n2
M ( m*)
D( m*)
np
n
npq
n2
p
pq
n
Т.о., оценка вероятности случайного события
р* является также несмещенной, т.е.
оценкой, математическое ожидание
которой равно оцениваемому параметру, и
асимптотически эффективной, т.е.
состоятельной оценкой, дисперсия которой
с увеличением объема выборки стремится
к нулю.