Похожие презентации:
Основные законы распределения. Равномерное распределение
1. ОСНОВНЫЕ ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
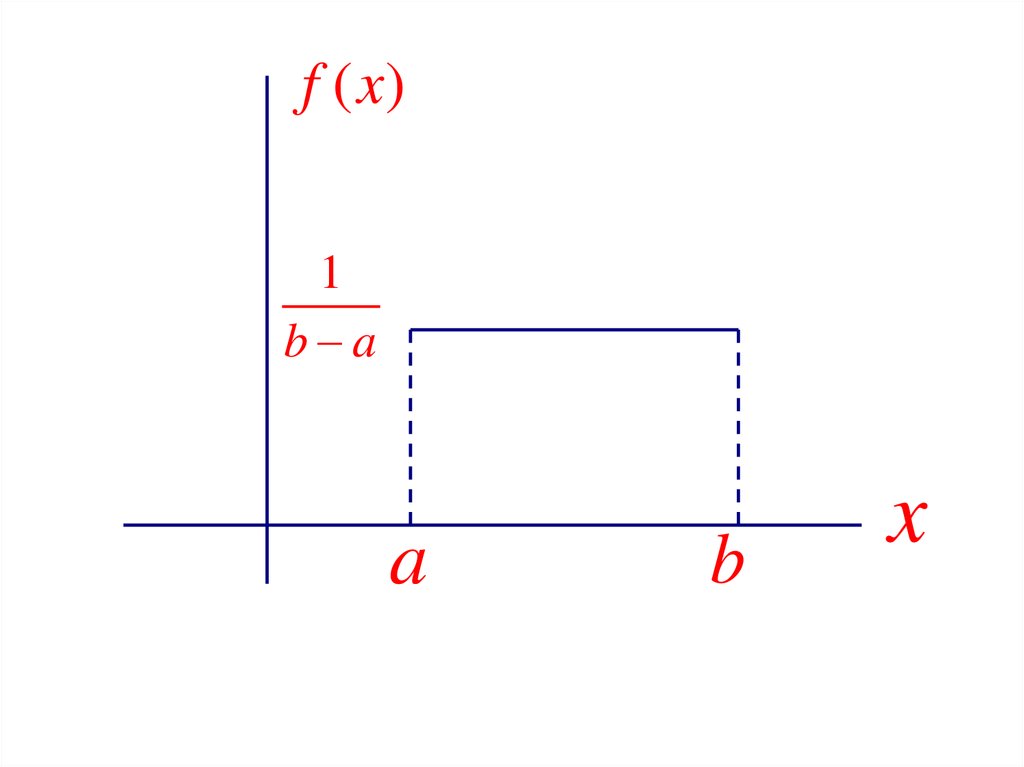
Равномерное распределение2.
Пусть плотность распределения случайнойвеличины является постоянной f ( x) const
a, b
на интервале
, и f ( x) 0
вне этого интервала.
Поскольку
f ( x)dx 1
b
C dx 1
, то
a
откуда
Cx a C (b a) 1
b
1
C
b a
.
3.
Таким образом, плотность распределенияравномерного закона представляется в виде
1
при x [a, b],
f ( x) b a
0 при x ( , a] [b, ).
4.
f ( x)1
b a
a
b
x
5.
Найдем математическое ожиданиеравномерного закона распределения.
b
2 b
1
1 x
M ( ) x
dx
b a
b a 2
a
a
1 b a
a b
.
b a 2
2
2
2
6.
Найдем дисперсию1
1 x
a b
2
D ( ) x
dx
b a
2 b a 3
a
b
2
3
b
a
( a b) 2
4
1 b3 a3 (a b) 2 b 2 ab a 2 b 2 2ab a 2
b a 3
4
3
4
4b 2 4ab 4a 2 3b 2 6ab 3a 2 b 2 2ab a 2
12
12
( a b) 2
.
12
7. ЗАДАЧА.
Диаметр гайки, которая изготавливаетсястанком-автоматом, есть равномерно
распределенная случайная величина
со средним значением 5 мм и средним
квадратическим отклонением 1 мм.
Определить интервал, из которого
принимает значения данная случайная
величина.
8. РЕШЕНИЕ.
Имеем:a b
M
5,
2
a b 10,
2
b a 2 3,
(b a) 2 1,
12
откуда a 5 3 3.3,
ОТВЕТ:
b 5 3 6.7.
[5 3,5 3].
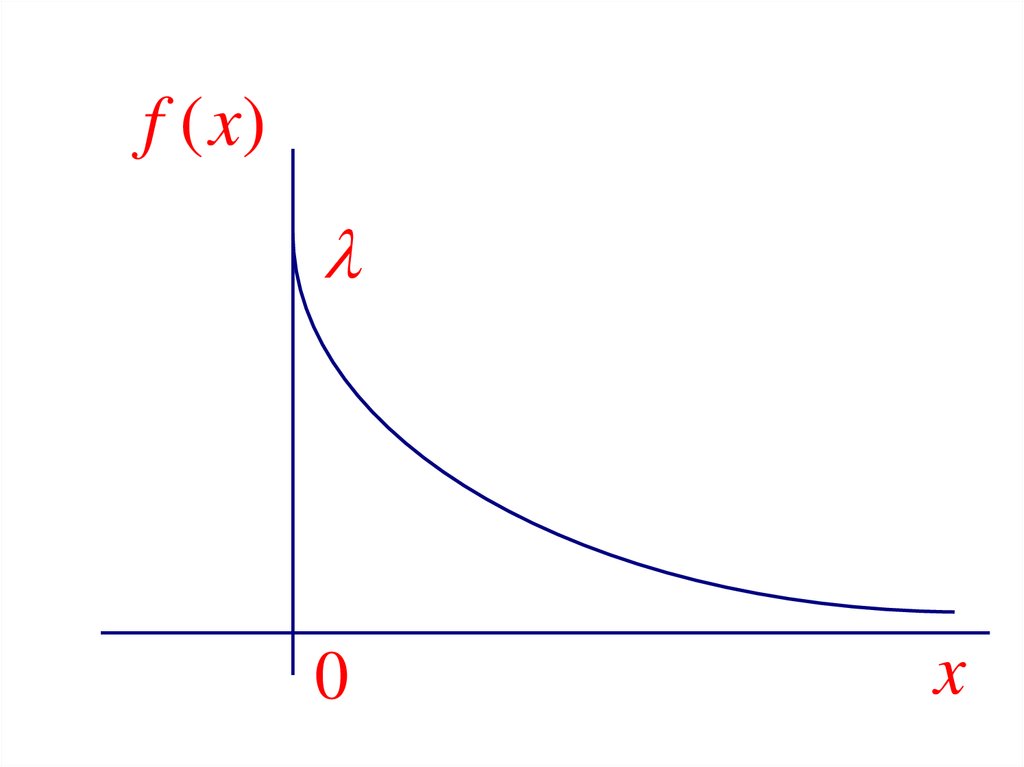
9. Показательное распределение.
Распределение называетсяпоказательным с параметром , если
плотность вероятности представляется
показательной функцией
x 0
0,
f ( x) x
e , x 0
10.
f ( x)0
x
11.
Найдем математическое ожиданиеслучайной величины, распределенной по
показательному закону.
M ( ) x e
0
x
dx xd (e
0
x
) xe
x
0
e
0
x
dx.
12.
k xxe
Отметим, что xlim
0
при любых положительных k и . Это
доказывается последовательным применением
правила Лопиталя.
Например, при k=1 получаем:
lim xe
x
x
x
lim x lim
x e
x
1
1
lim x 0.
x e
x
e
x
13.
Возвращаясь к вычислению математическогоожидания, получаем
xe
x
0
e
x
dx 0 0
e
0
e
e
0 e
0
e
0
x
0
1
.
14. УПРАЖНЕНИЕ.
Доказать, что дисперсия случайной величины,распределенной по показательному закону,
равна
D( ) x e
2
0
2
x
1
1
dx 2 .
15. ЗАДАЧА.
Время службы электрической лампочки естьслучайная величина, распределенная по
показательному закону.
Найти вероятность того, что лампочка будет
работать не меньше 120 часов,
если среднее время работы лампочки составляет
240 часов.
16. РЕШЕНИЕ.
Поскольку математическое ожиданиеслучайной величины, распределенной по
показательному закону, равно
1
имеем
1
1
240
.
240
17.
Следовательно, плотность распределениявремени службы лампочки имеет вид
x 0
0,
x / 240
f ( x) e
240 , x 0
18.
Искомая вероятность равнаP{ 120}
120
e
x / 240 x
x 120
e
e
x / 240
240
1/ 2
dx
1
0.606.
e
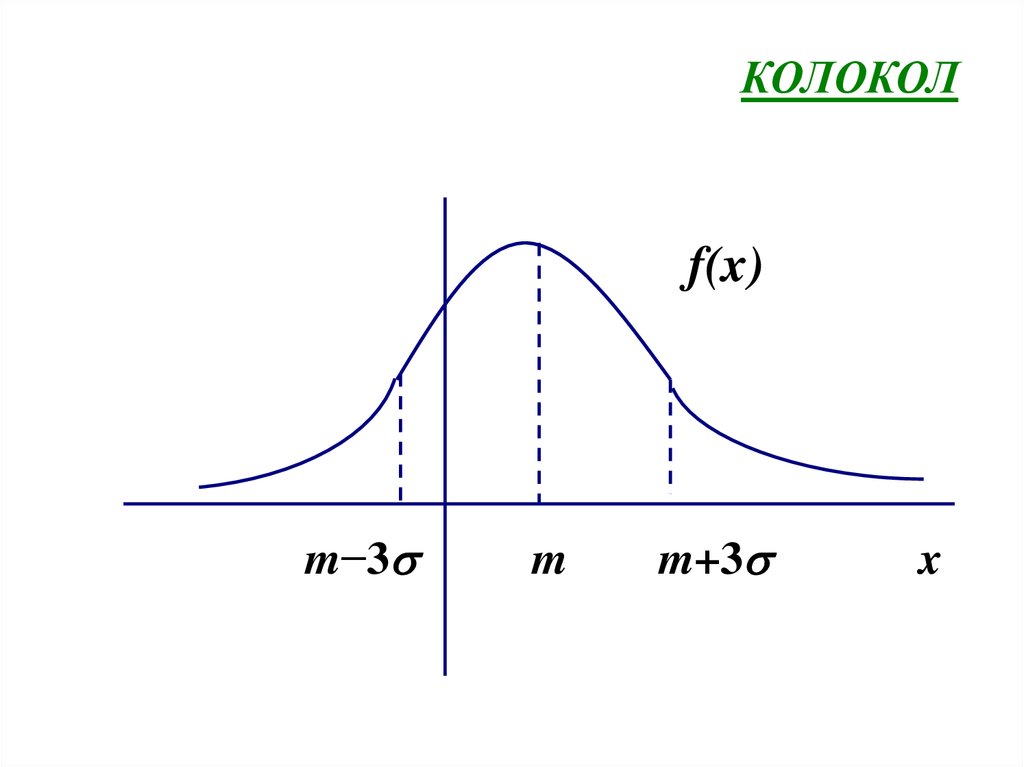
19. Нормальное распределение.
Случайная величина распределена нормально,если плотность вероятности представляется в
виде.
1
f ( x)
e
2
1 x a
2
2
.
20.
Функция плотности зависит от двухвещественных параметров a и ,
где a математическое ожидание, а
среднее квадратическое отклонение.
Обозначается нормально распределенная
случайная величина
N ( a, )
21.
КОЛОКОЛf(x)
m−3
m
m+3
x
22.
Основная трудность с вычислениями,связанными с нормальным законом
распределения, заключается в том, что функция
1
e
2
1 2
x
2
не может быть проинтегрирована в
элементарных функциях.
23.
1e
2
Одна из первообразных функции
1
x2
2
функция Лапласа, затабулирована, и ее значения
можно найти в статистических таблицах.
Функция Лапласа задается соотношением
x
( x)
1
e
2 0
1 2
t
2
dt.
24.
Из определения следует, что функцияЛапласа нечетная и монотонно
возрастающая.
При этом
lim ( x) 0.5,
x
lim ( x) 0.5.
x
25.
Вероятность попадания случайной величиныN ( a, )
на заданный промежуток вычисляется по формуле:
1
P ( )
e
2
( x a )2
2 2
dx
a
a
.
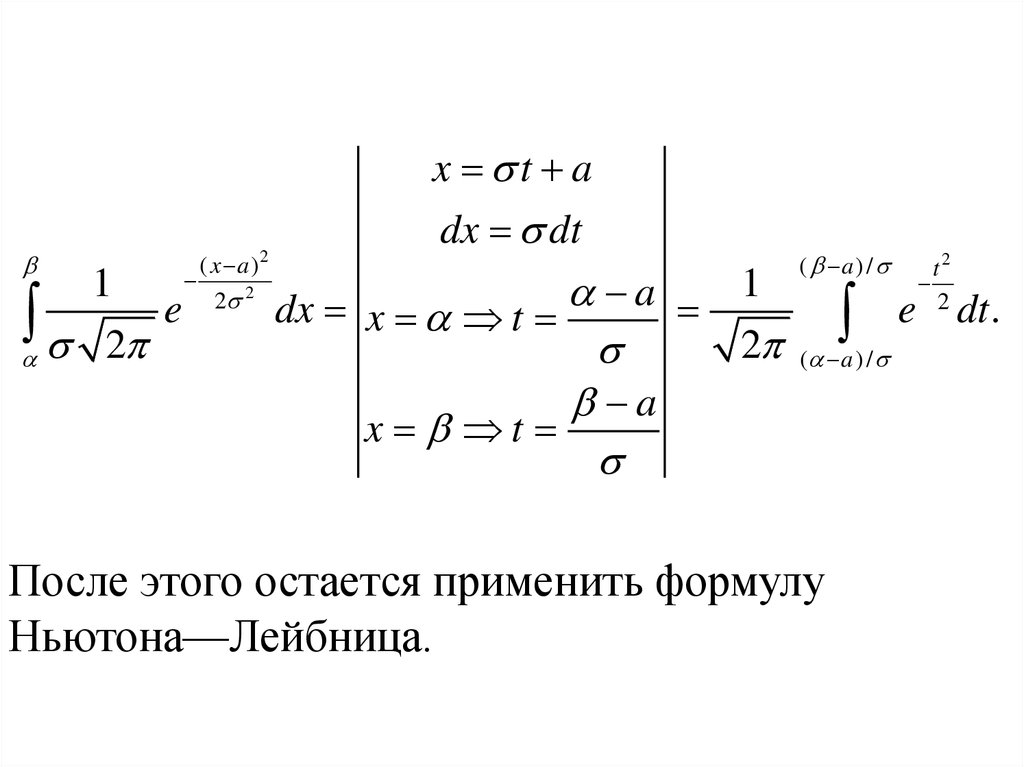
26.
Чтобы убедиться в этом, надо сделать заменупеременной
x a
t
под знаком определенного интеграла:
27.
x t a1
2 e
( x a )2
2 2
dx dt
1
a
dx x t
2
a
x t
( a ) /
( a ) /
После этого остается применить формулу
Ньютона—Лейбница.
t2
2
e dt.
28. ПРИМЕР.
Математическое ожидание нормальнораспределенной случайной величины равно 10,
а дисперсия 4.
Записать плотность вероятности и вычислить
вероятность попадания случайной величины на
интервал (12, 14).
29. РЕШЕНИЕ.
Имеем: a=10, 2=4,1
f ( x)
e
2 2
( x 10) 2
8
.
14 10
12 10
P(12 14)
2
2
(2) (1) 0,4772 0,3413 0,1359.
30. Правило “трех сигм”.
Найдем вероятность отклонения нормальнораспределенной случайной величины от своего
математического ожидания.
P( a ) P(a a )
a a
a a
2 .
31.
Обозначимt , t.
При t 1
P( a ) 2 (1) 2 0,3413 0,6826
t 2
P( a 2 ) 2 (2) 2 0, 4772 0,9544
t 3
P( a 3 ) 2 (3) 2 0, 49865 0,9973
32.
ВЫВОД: если случайная величина распределенанормально,
то ее отклонение от математического ожидания с
вероятностью 0,9973
не превосходит утроенного среднего
квадратического отклонения.
33. РАСПРЕДЕЛЕНИЯ, СВЯЗАННЫЕ С НОРМАЛЬНЫМ
2─РАСПРЕДЕЛЕНИЕ
34.
Пусть1 , , n
– независимые одинаково нормально
распределенные случайные величины с
математическим ожиданием a и средним
квадратичным уклонением . Тогда случайная
n
величина
1
2
2
2 ( i )
i 1
1
где
( 1 n )
n
называется распределением 2 с
степенями свободы.
n
35.
Плотность2
−распределения определяется функцией
2x n2 1
f ( x, n) Ke x , при x 0,
0, при x 0.
36.
Константа K определяется из условиявероятностной нормировки
Интеграл вида
f ( x, n)dx 1
0
(t ) x e dx, t 0,
t 1 x
0
в математическом анализе называется
Гамма−функцией. Следовательно,
.
K
1
n
2
n
2 ( )
2
37.
Математическое ожидание−распределения равно M n
2
дисперсия равна D 2n
38.
Предположим теперь, что среди исходныхнормально распределенных случайных величин
1 , , n
не все n величин независимы, но имеется s
линейных соотношений типа равенства.
39.
Оказывается, что тогда случайная величина2
1
2
n
(
i 1
i
)
2
по-прежнему, имеет распределение такого же
вида, что и прежде, но с меньшим числом
степеней свободы n s
1
2
f ( x, ) Ke x , при x 0,
0, при x 0.
x
2
40.
Это обстоятельство часто используется приоценивании параметров распределений в
математической статистике
41.
В дальнейшем нам понадобится понятие2
критической точки распределения
с уровнем значимости
Это – решение уравнения
P ( )
2
Значения
2
2
2
f ( x, n) dx 1 .
0
как функции от числа степеней свободы n и
уровня значимости затабулированы и
приводятся во всех учебниках по
математической статистике.
42. РАСПРЕДЕЛЕНИЕ СТЬЮДЕНТА
Пусть Z стандартная нормально распределеннаяслучайная величина N(0,1), а U − независимая от
нее 2−распределенная случайная величина с
степенями свободы. Тогда случайная величина
Z
T
U
называется t−распределением, или
распределением Стьюдента с степенями
свободы.
43.
Плотность распределения Стьюдента имеет видf ( x, ) B (1
x
1
2
)
2
.
Константа B определяется из условия
вероятностной нормировки.
Для распределения Стьюдента математическое
ожидание равно 0, а дисперсия равна
2
44.
Для распределения Стьюдента можноопределить критические точки распределения,
аналогично тому, как
это
было
сделано
для
2
распределения
P (T t )
t
0
f ( x, ) dx 1 .


























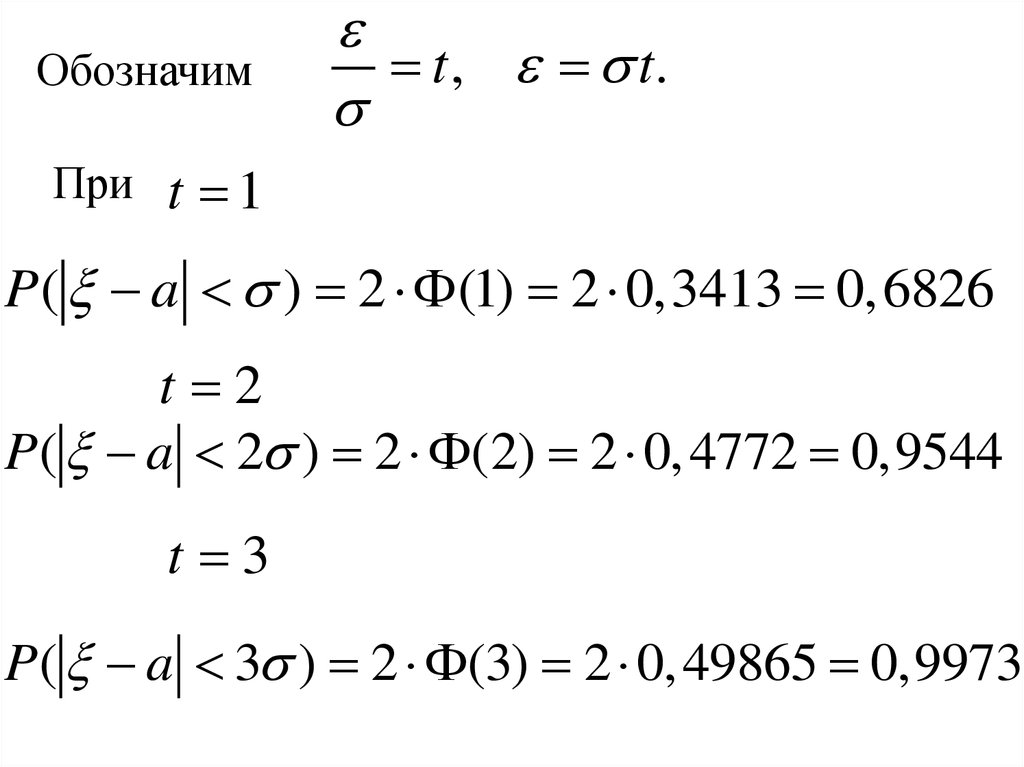













 Математика
Математика








