Методы многокритериального анализа альтернатив для слабоструктурированных проблем

1. Методы многокритериального анализа альтернатив для слабоструктурированных проблем

Кондрашина Ольга Николаевна
[email protected]

2. Понятие слабоструктурированных проблем

Право, такое затруднение — выбор! Если бы еще
один, два человека, а то четыре. Как хочешь, так
и выбирай. Никанор Иванович недурен, хотя,
конечно, худощав; Иван Кузьмич тоже недурен. Да
если сказать правду, Иван Павлович тоже хоть и
толст, а ведь очень видный мужчина. Прошу
покорно, как тут быть? Балтазар Балтазарович
опять мужчина с достоинствами. Уж как трудно
решиться, так просто рассказать нельзя, как
трудно! Если бы губы Никанора Ивановича да
приставить к носу Ивана Кузьмича, да взять
сколько-нибудь развязности, какая у Балтазара
Балтазарыча, да, пожалуй, прибавить к этому
еще дородности Ивана Павловича — я бы тогда
тотчас же решилась. А теперь поди подумай!
просто голова даже стала болеть.
Н.В. Гоголь «Женитьба»

3. Альберт Энштеин

• Если бы мне был
отведен всего один час
на спасение мира, я
потратил бы 55 минут
на анализ проблемы и
лишь оставшиеся пять
минут - на ее решение.
• А.Эйнштейн
Альберт Энштеин

4. Понятие слабоструктурированных проблем

• Слабоструктурированными являются проблемы,
как правило, сложные, отличающиеся в первую
очередь, качественными зависимостями между
элементами ситуации.
• При этом сами элементы могут быть как
качественными, так и количественными.
• Это область применения системного анализа. В
решении подобных проблем применяется
сочетание количественных и эвристических
методов.

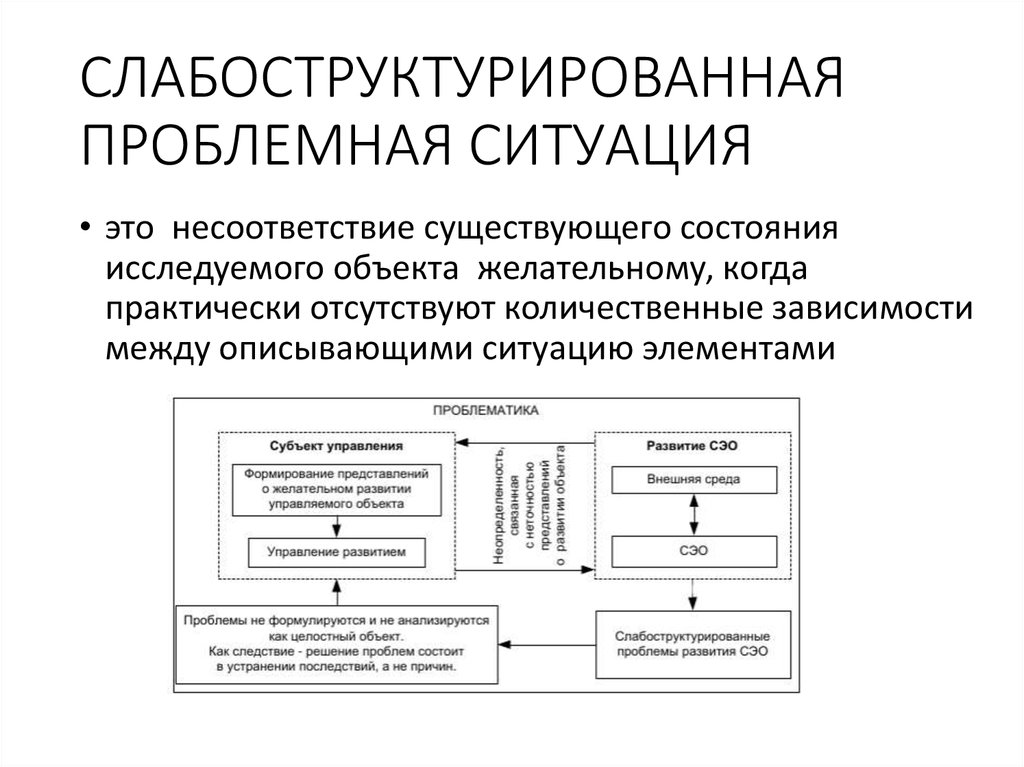
5. СЛАБОСТРУКТУРИРОВАННАЯ ПРОБЛЕМНАЯ СИТУАЦИЯ

• это несоответствие существующего состояния
исследуемого объекта желательному, когда
практически отсутствуют количественные зависимости
между описывающими ситуацию элементами

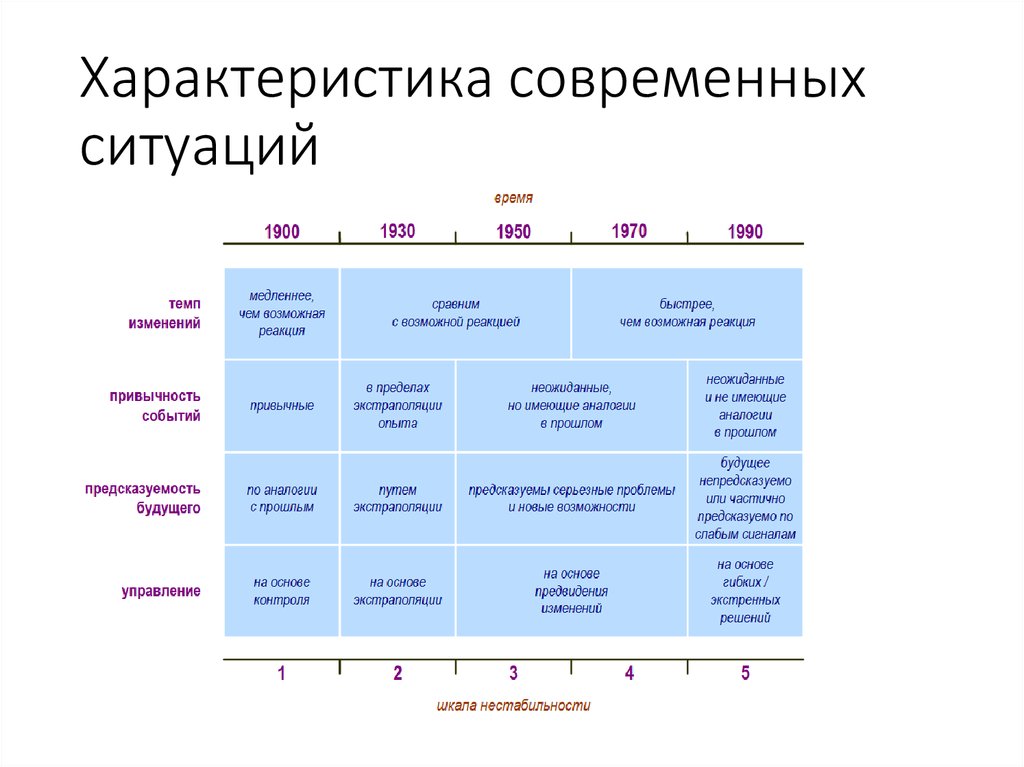
6. Характеристика современных ситуаций

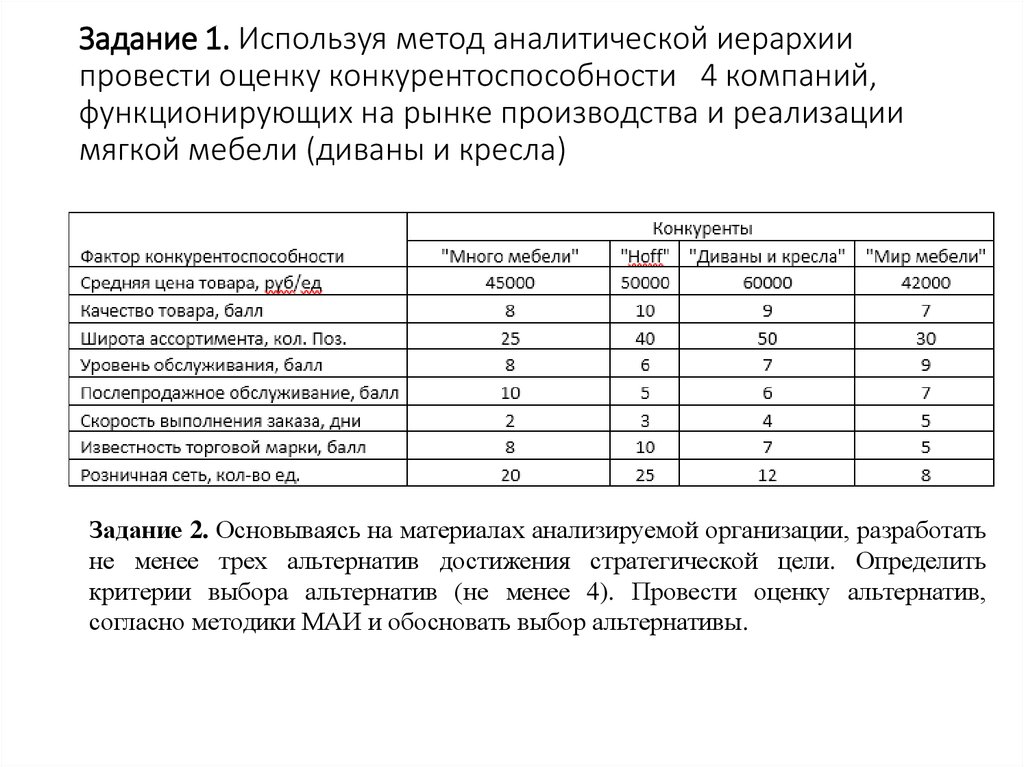
7. Метод аналитической иерархии (МАИ)

• математический инструмент
системного подхода к
решению проблем принятия
решений.
• МАИ не предписывает лицу,
принимающему решение,
какого-либо «правильного»
решения, а позволяет ему в
интерактивном режиме
найти такой вариант
(альтернативу), который
наилучшим образом
согласуется с его
пониманием сути проблемы
и требованиями к ее
решению.
• Высокая универсальность –
метод может применяться для
решения самых разнообразных
задач: анализа возможных
сценариев развития ситуации,
распределения ресурсов,
составления рейтинга
клиентов, принятия кадровых
решений и др.
Необходимость получения большого
объема информации от экспертов.

8. Метод аналитической иерархии (МАИ)

• Метод разработан
американским ученым
Томасом Л. Саати в 1970
году, с тех пор он
активно развивается и
широко используется на
практике
• Метод в наибольшей мере
подходит для тех случаев, когда
основная часть данных основана
на предпочтениях лица,
принимающего решения, в
процессе выбора наилучшего
варианта решения из множества
существующих альтернатив

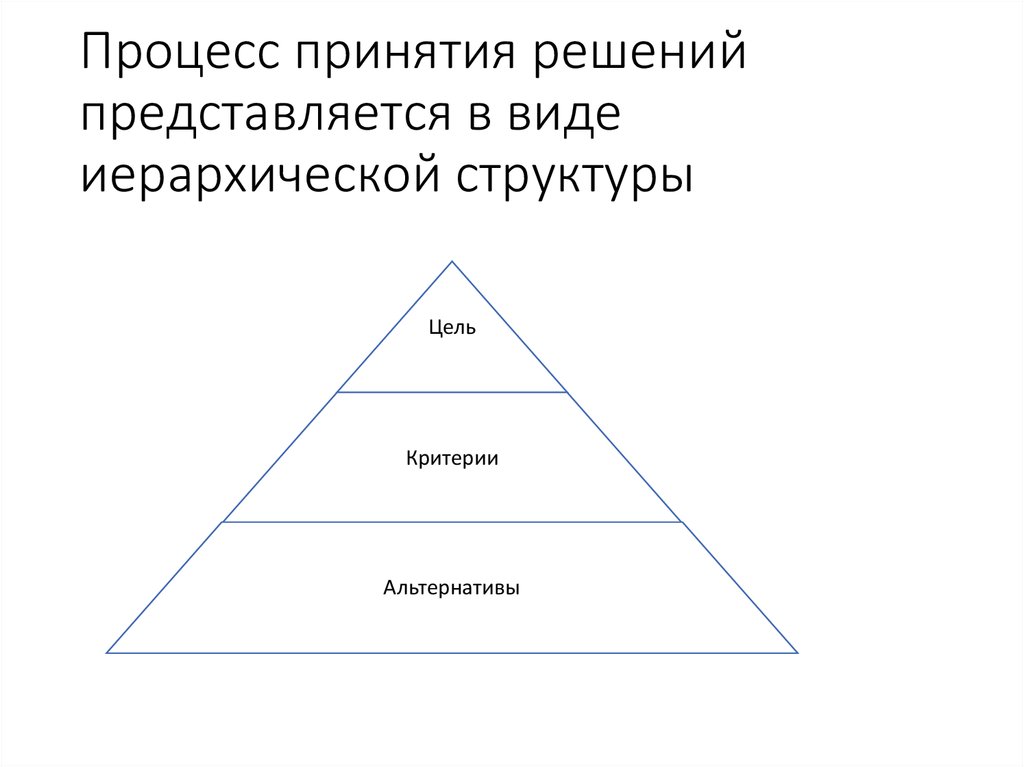
9. Процесс принятия решений представляется в виде иерархической структуры

Цель
Критерии
Альтернативы

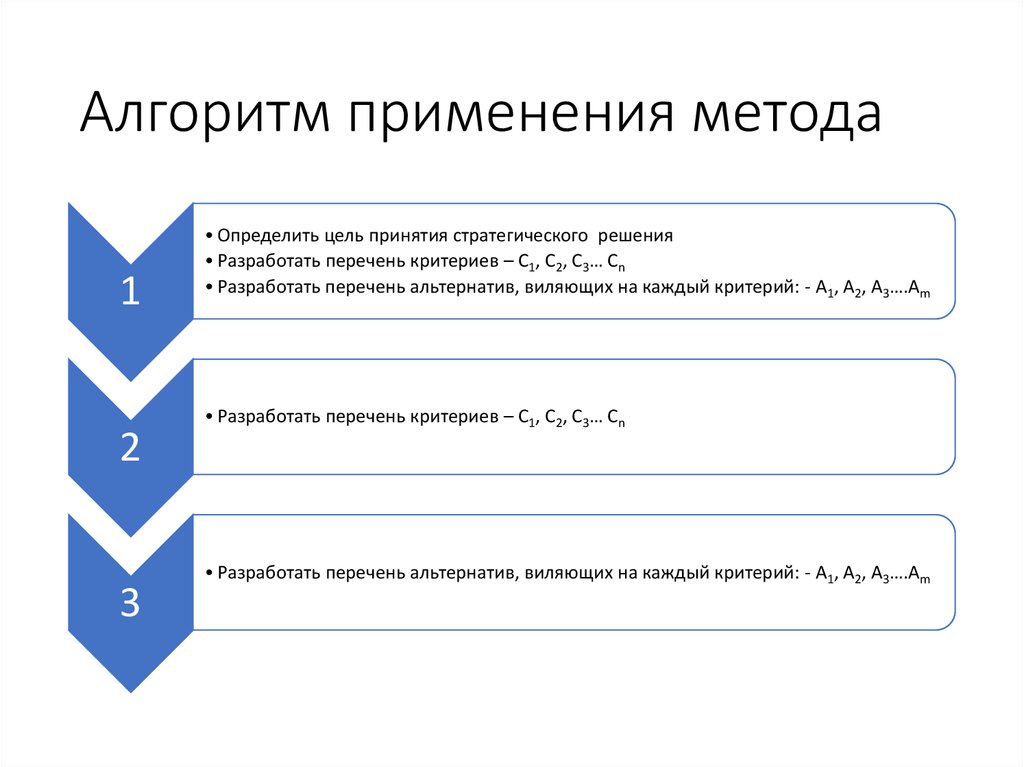
10. Алгоритм применения метода

1
2
3
• Определить цель принятия стратегического решения
• Разработать перечень критериев – С1, С2, С3… Сn
• Разработать перечень альтернатив, виляющих на каждый критерий: - А1, А2, А3….Аm
• Разработать перечень критериев – С1, С2, С3… Сn
• Разработать перечень альтернатив, виляющих на каждый критерий: - А1, А2, А3….Аm

11. Алгоритм применения метода

4
• Попарное сравнение альтернатив и критериев. Ответить на вопрос – Какая
альтернатива предпочтительная, имеет большее воздействие или более вероятная
для данного критерия. Используется следующая шкала:
Шкала сравнения альтернатив
Равная важность альтернатив
Умеренное превосходство
Существенное превосходство
Значительное превосходство
Очень большое превосходство
Значение
1
3
5
7
9

12. Алгоритм применения метода

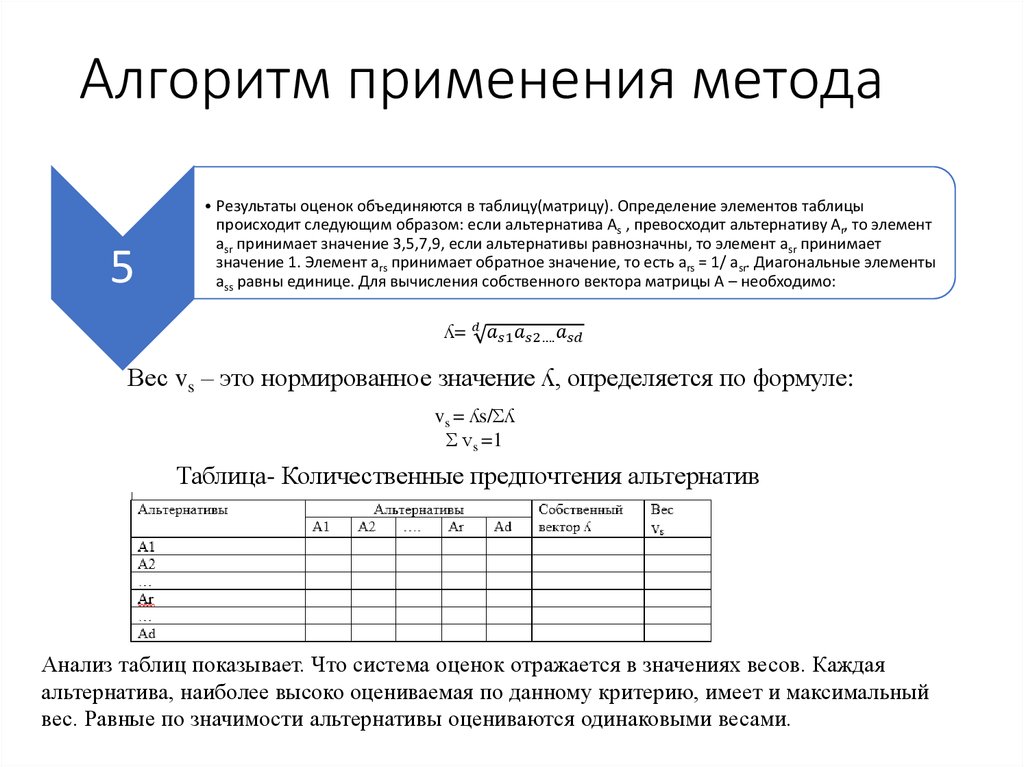
5
• Результаты оценок объединяются в таблицу(матрицу). Определение элементов таблицы
происходит следующим образом: если альтернатива Аs , превосходит альтернативу Аr, то элемент
asr принимает значение 3,5,7,9, если альтернативы равнозначны, то элемент asr принимает
значение 1. Элемент ars принимает обратное значение, то есть ars = 1/ asr. Диагональные элементы
ass равны единице. Для вычисления собственного вектора матрицы А – необходимо:
ʎ=