Похожие презентации:
Термодинамика и статистическая физика
1. Термодинамика и статистическая физика
2. Лекция № 5
Закон распределения Больцмана.1. Система частиц во внешнем силовом поле.
2. Закон распределения Больцмана для
равновесного состояния системы.
3. Барометрическая формула.
Теплоёмкость многоатомных газов.
1. Число степеней свободы. Равномерное
распределение средней кинетической энергии
теплового движения по степеням свободы.
2. Классическая теория теплоёмкости
многоатомных газов и её ограниченность.
“Замороженные” степени свободы.
3.
В отсутствие внешних сил средняяконцентрация n молекул газа в состоянии равновесия всюду одинакова.
Но этого не будет при наличии силовых полей. Рассмотрим, например,
идеальный газ в однородном поле
тяжести. В состоянии равновесия
температура Т должна быть одинакова
по всей толще газа (иначе возникли
бы потоки тепла). Для механического
равновесия необходимо, чтобы
4.
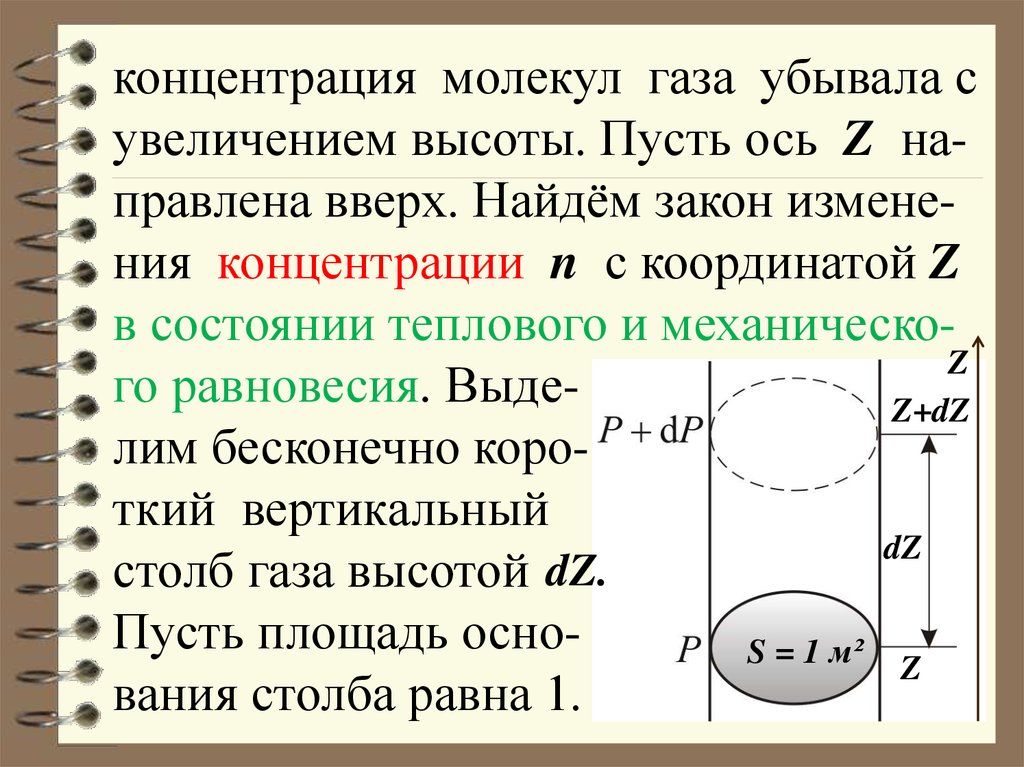
концентрация молекул газа убывала сувеличением высоты. Пусть ось Z направлена вверх. Найдём закон изменения концентрации n с координатой Z
в состоянии теплового и механическоZ
го равновесия. ВыдеZ+dZ
лим бесконечно короткий вертикальный
dZ
столб газа высотой dZ.
Пусть площадь осноS = 1 м² Z
вания столба равна 1.
5.
6.
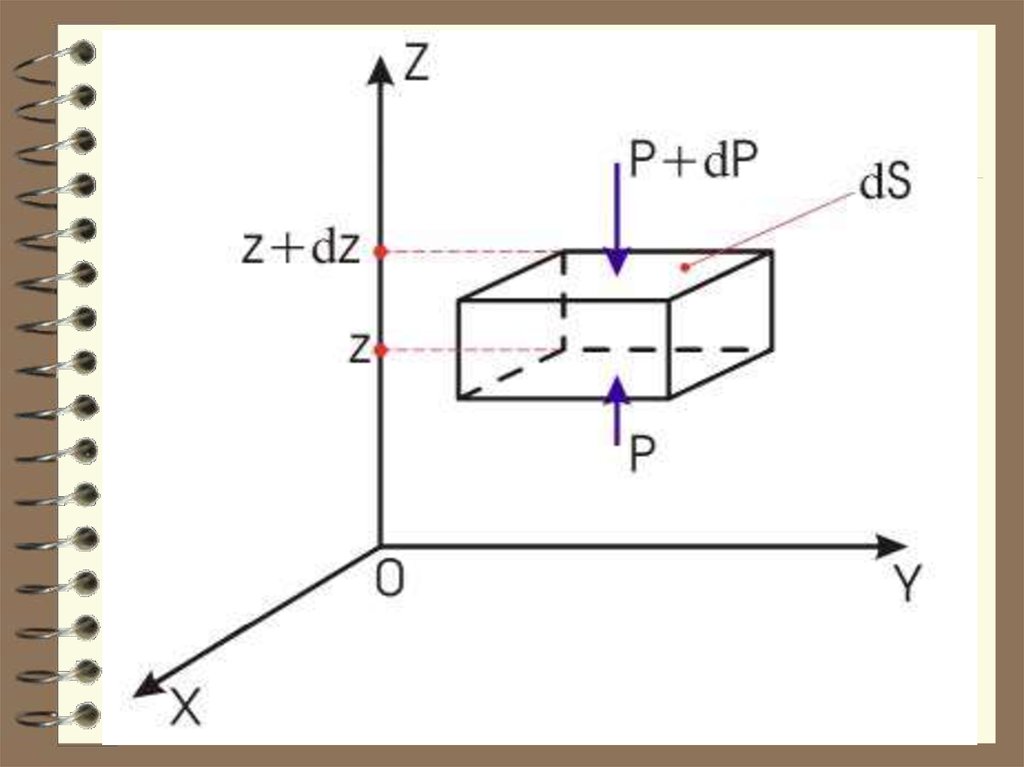
Вес столба n mg dZ S должен уравновешиваться разностью давлений:dP
P ( P dP) dP
dZ n mg dZ S
dZ
dP
n mg , т.к. S = 1 м²
dZ
т.к.
Z
Z+dZ
P nkT
dP
dn
kT
n mg
dZ
dZ
kTd ln n mg dZ
dZ
S = 1 м²
Z
7.
Физическая природа силового поля неимеет значения. Важно, чтобы поле
было постоянно и консервативно
(потенциально). Если Ep – потенциальная энергия молекулы в силовом
поле, то mg∙dZ = dEp, а потому
получаем: kTd ln n dE
kT d ln n dE p
p
kT ln n Е р kT ln no
8.
nkT ln
Е р
no
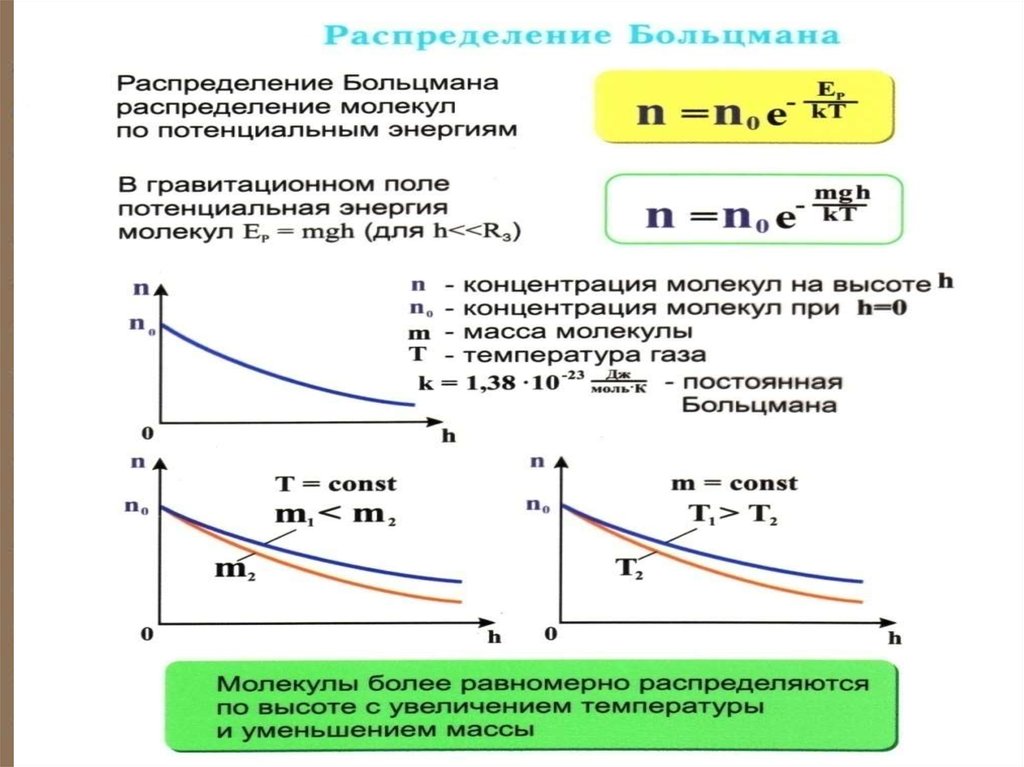
n no e
Ер
kT
- закон
распределения
Больцмана
Закон распределения частиц по потенциальным энергиям – распределение
Больцмана.
Здесь n0 – число молекул в
единице объёма там, где Е р 0 .
9.
10. Больцман Людвиг (1844 – 1906) – австрийский физик- теоретик, один из основопо- ложников классической статистической физики.
Больцман Людвиг (1844 –1906) – австрийский физиктеоретик, один из основоположников классической
статистической физики.
Основные работы в области
кинетической теории газов, термодинамики и теории излучения. Вывел основное кинетическое уравнение газов, являющееся основой физической кинетики.
11. Пусть идеальный газ находится в поле консервативных сил, в условиях теплового равновесия. При этом, концентрация газа будет
различной вточках с различной потенциальной
энергией, что необходимо для соблюдения условий механического равновесия.
Число молекул в единичном объеме n
убывает с удалением от поверхности
Земли, и давление, в силу соотношения
убывает.
P nkT тожеhttp://ido.tsu.ru/schools/physmat/da
ta/res/models/text/molek2.htm
12.
13. С уменьшением температуры число молекул на высотах, отличных от нуля, убывает. При тепловое движение прекращается, все молекулы
С уменьшением температурычисло молекул на высотах, отличных
от нуля, убывает. При T 0
тепловое движение прекращается, все
молекулы расположились бы на земной
поверхности.
При высоких температурах,
наоборот, молекулы оказываются
распределёнными по высоте почти
равномерно, а плотность молекул
медленно убывает с высотой.
14.
Распределение Больцмана можно представить в виде ( Ер = mgh ):n n0e
Зависимость
концентрации
различных газов от
высоты. Видно, что
число более
тяжелых молекул с
высотой убывает
быстрее, чем легких.
mgh
kT
15.
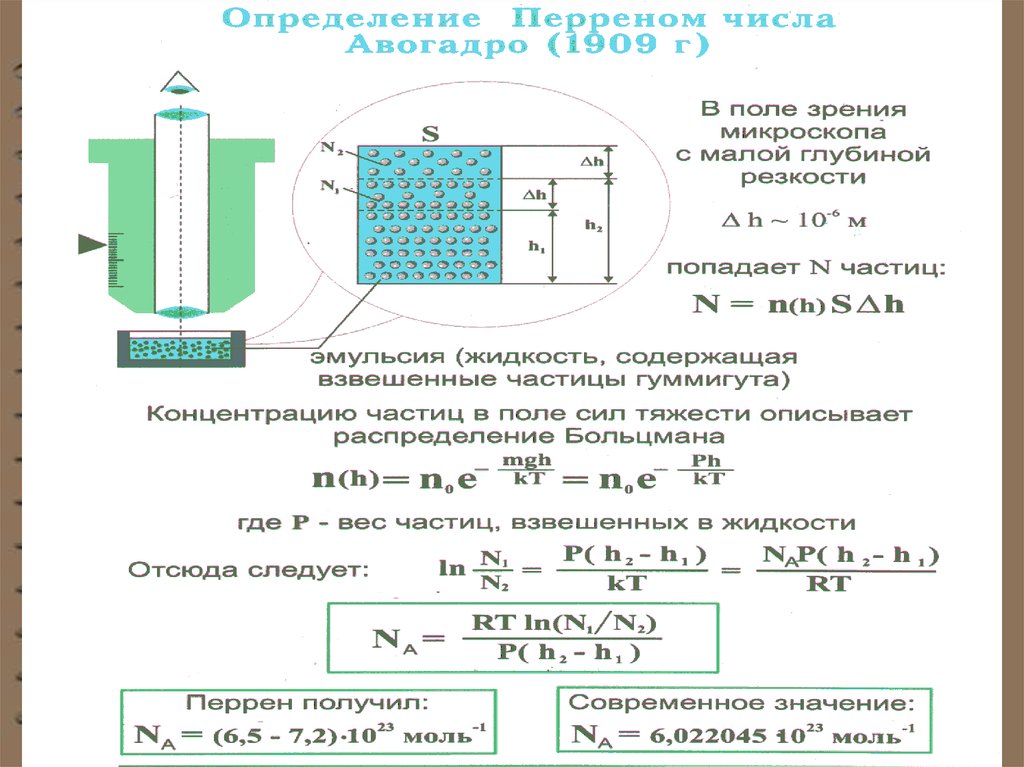
Опытное определение постоянной Авогадро. Ж. Перренвоспользовался идеей распределения молекул по высоте
и экспериментально определил значение постоянной
Авогадро. Исследуя броуновское движение, он убедился,
что броуновские частицы распределяются по высоте
подобно молекулам газа в поле тяготения. Применив к
ним больцмановское распределение, можно записать
где
(m m1 ) gh
n n0 exp
kT
m1 - масса вытесненной
m - масса частицы,
4
3
m r
3
r
- радиус частицы,
- плотность частицы,
ею жидкости;
4
m1 r 3 1
3
1 - плотность жидкости.
16.
Еслиа k
n1 и n 2 - концентрации частиц на уровнях h1 и h2 ,
R/ NA
, то
3RT ln( n1 / n2 )
NA
3
4 r ( 1 )( h2 h1 )
Значение N A , полученное из работ Ж. Перрена,
соответствовало значениям, полученным в других
опытах, что подтверждает применимость к броуновским
частицам распределения Больцмана.
17.
18. Закон распределения Максвелла-Больцмана
Закон распределения МаксвеллаБольцманаНа прошлой лекции мы получили
выражение для распределения молекул по
скоростям (распределение Максвелла),
т.е. число молекул в единице объёма,
скорости которых лежат в пределах от υ
до υ dυ равно:
m
dn( υ) 4 n
2 kT
3/ 2
e
mυ 2
2 kT
d
2
19. Закон Максвелла даёт распределение частиц по значениям кинетической энергии Екин, а закон Больцмана – распределение частиц по
значениямпотенциальной энергии Ер. Оба распределения можно объединить в единый закон
Максвелла-Больцмана, согласно которому,
число молекул в единице объёма, скорости
которых лежат в пределах от υ до υ dυ
равно:
dnЕ р , Екин
m
n0 4
2 kT
3/ 2
e
Е р Екин
kT
d
2
20. Обозначим – полная энергия. Тогда Это и есть закон распределения Максвелла-Больцмана. Здесь n0 – число молекул в единице объёма
Обозначим E Е р Екин – полнаяэнергия. Тогда
dn n0 Ae
E
kT
d
2
Это и есть закон распределения
Максвелла-Больцмана. Здесь n0 –
число молекул в единице объёма в той
3/ 2
точке, где Е р 0 ;
m
A 4
2 kT
21. В последнем выражении, потенциальная и кинетическая энергии, а следовательно и полная энергия Е, могут принимать непрерывный
ряд значений. Если жеэнергия частицы может принимать лишь
дискретный ряд значений Е1, Е2 ... (как
это имеет место, например, для внутренней энергии атома), то в этом случае
распределение Больцмана имеет вид:
N i Ae
Ei
kT
,
22. где Ni – число частиц, находящихся в состоянии с энергией Еi, а А – коэффициент пропорциональности, который должен
удовлетворятьусловию:
N
N
Ν i A e
i 1
Ei
kT
N,
i 1
где N – полное число частиц в
рассматриваемой системе.
23. Тогда, окончательное выражение распределения Масвелла-Больцмана для случая дискретных значений будет иметь вид:
NiNe
e
Ei
Ei
kT
kT
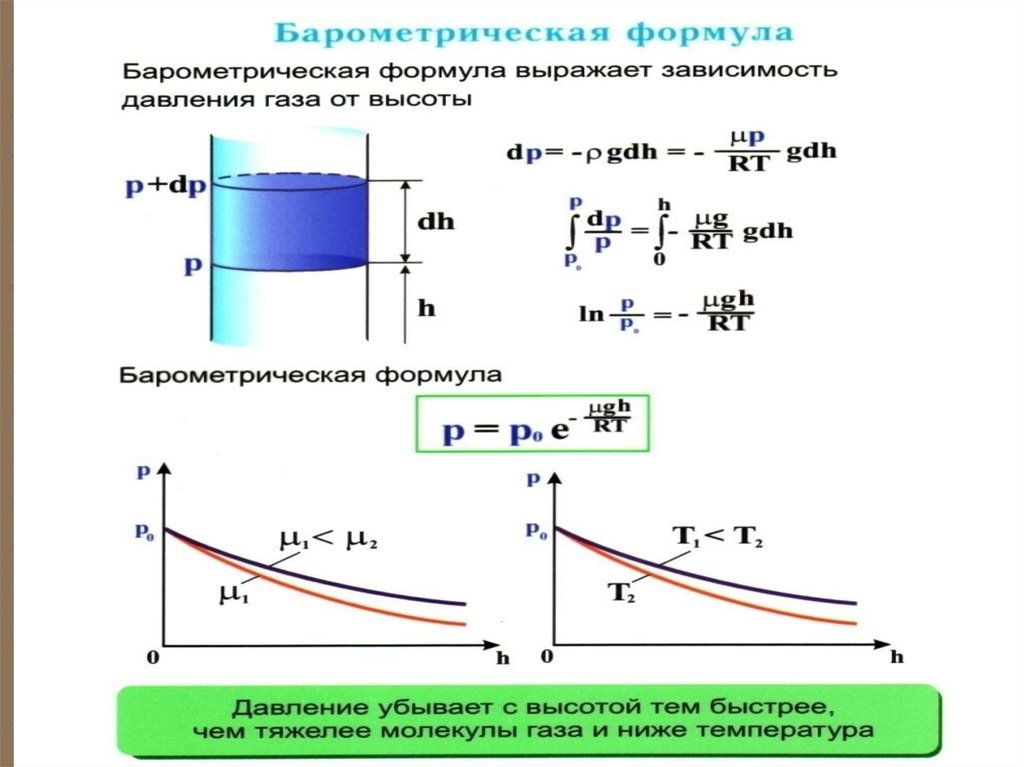
24. Барометрическая формула
Атмосферное давление на какойлибо высоте h обусловлено весомвыше лежащих слоёв газа.
Пусть P – давление на высоте h,
а P ΔP – на высоте h Δh .
Выведем закон изменения давления с высотой, предполагая, что 1) поле тяготения
однородно, 2) температура постоянна и
3) масса всех молекул одинакова.
25.
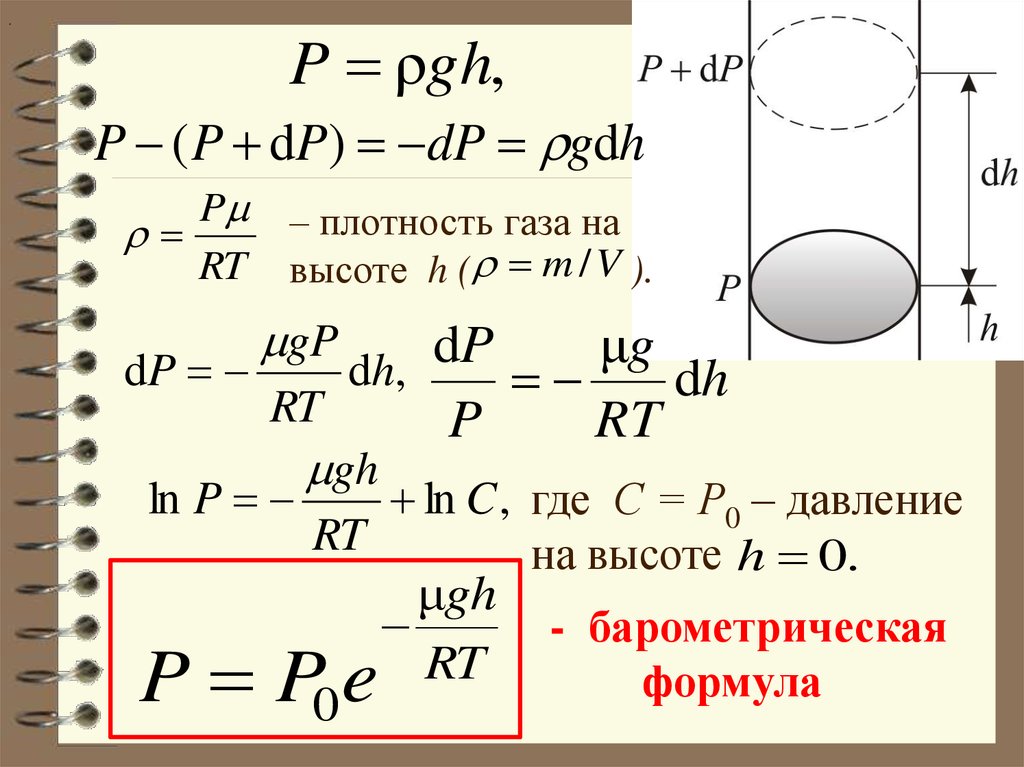
.P ρgh,
P ( P dP) dP gdh
P – плотность газа на
RT высоте h ( m / V ).
gP
d
P
μ
g
dP
dh,
d
h
RT
P
RT
ln P
gh
ln C , где С = Р0 – давление
RT
на высоте h 0.
μgh
- барометрическая
RT
формула
0
P Pe
26. Причём , dР < 0, так как на большей высоте давление меньше. Раз-ность давления равна весу газа, заключённого в объёме цилиндра
Причём dh 0 , dР < 0, так как набольшей высоте давление меньше. Разность давления P ( P dP) равна весу
газа, заключённого в объёме цилиндра с
площадью основания равного единице и
высотой dh, P ρgh, ρ плотность газа
на высоте h, медленно убывает с
высотой. P ( P dP) ρgdh,
Отсюда
P P0 e
gh
RT
- барометрическая
формула
где P0 – давление на высоте h 0.
27. Из барометрической формулы следует, что P убывает с высотой тем быстрее, чем тяжелее газ (чем больше μ) и чем ниже температура
(например, на большихвысотах концентрация легких газов Не и
Н2 гораздо больше чем у поверхности
Земли).
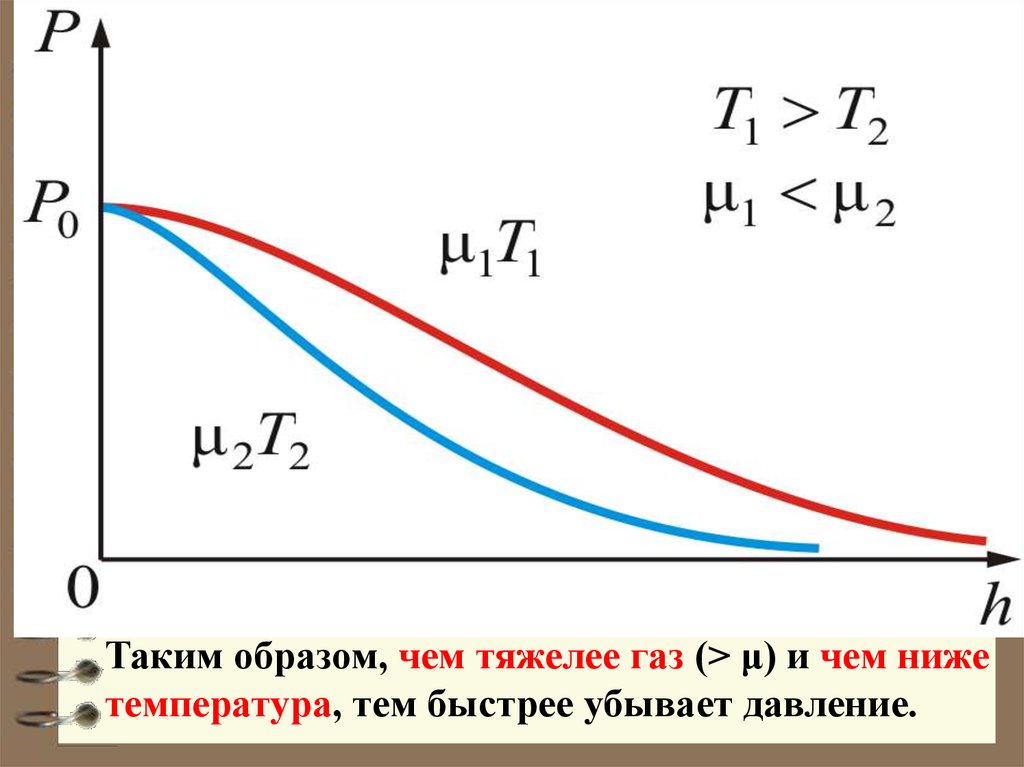
На рисунке изображены две кривые,
которые можно трактовать, либо как
соответствующие разным μ (при
одинаковой Т), либо как отвечающие
разным Т, при одинаковых μ.
28.
Таким образом, чем тяжелее газ (> μ) и чем нижетемпература, тем быстрее убывает давление.
29.
30.
АтмосфераЗемли
31.
32. Строение атмосферы
33. Распределение Бозе-Эйнштейна и Ферми-Дирака
Если у нас имеется термодинамическая система состоящая из N частиц,энергии которых могут принимать
дискретные значения , то говорят о
системе квантовых чисел.
Поведение такой системы описывается квантовой статистикой, в основе которой лежит принцип неразличимости тождественных частиц.
34. Основная задача квантовой статистики состоит в определении среднего числа частиц , находящихся в ячейке фазового пространства:
Основная задача квантовой статистикисостоит в определении среднего числа
частиц Ni , находящихся в ячейке
фазового пространства: «координаты –
проекции импульса» (x, y, z и px, py, pz)
частиц.
При этом имеют место два закона
распределения частиц по энергиям (две
статистики):
35. распределение Бозе-Эйнштейна: ; распределение Ферми-Дирака: .
распределение Бозе-Эйнштейна:1
N i
( Ei μ )
kT
e
;
1
распределение Ферми-Дирака:
1
N i
( Ei μ )
e
kT
.
1
36. Первая формула описывает квантовые частицы с целым спином (собственный момент количетсва движения). Их называют бозоны
(например, фотоны).Вторая формула описывает
квантовые частицы с полуцелым
спином. Их называют фермионы
(например: электроны, протоны,
нейтрино).
37.
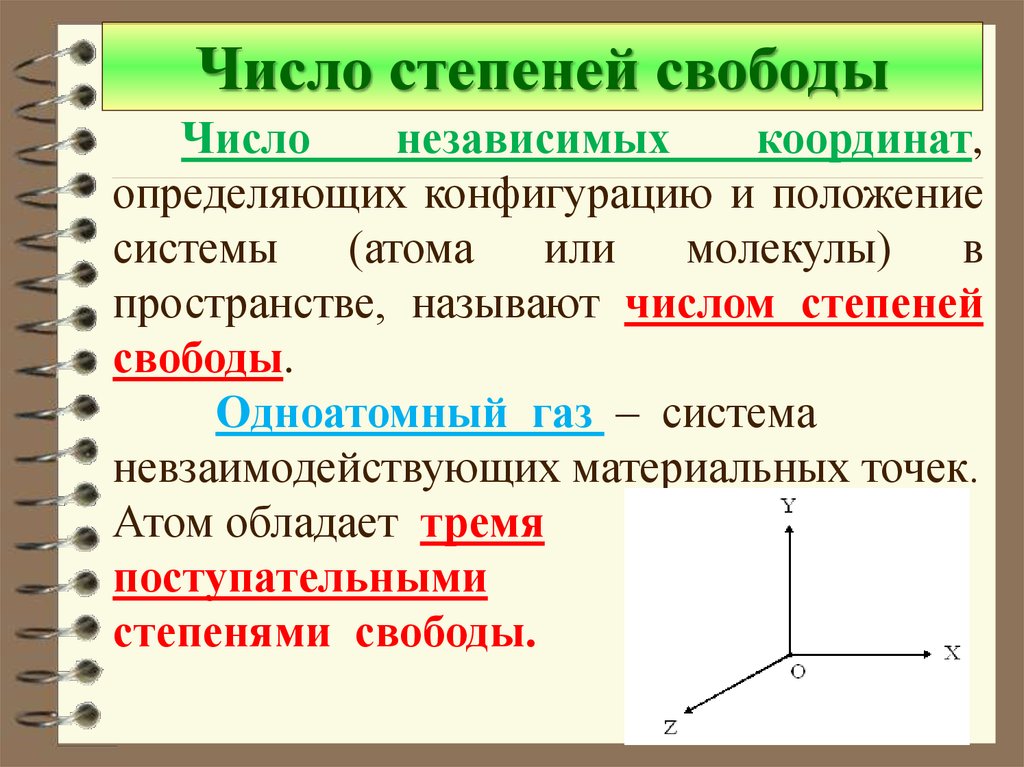
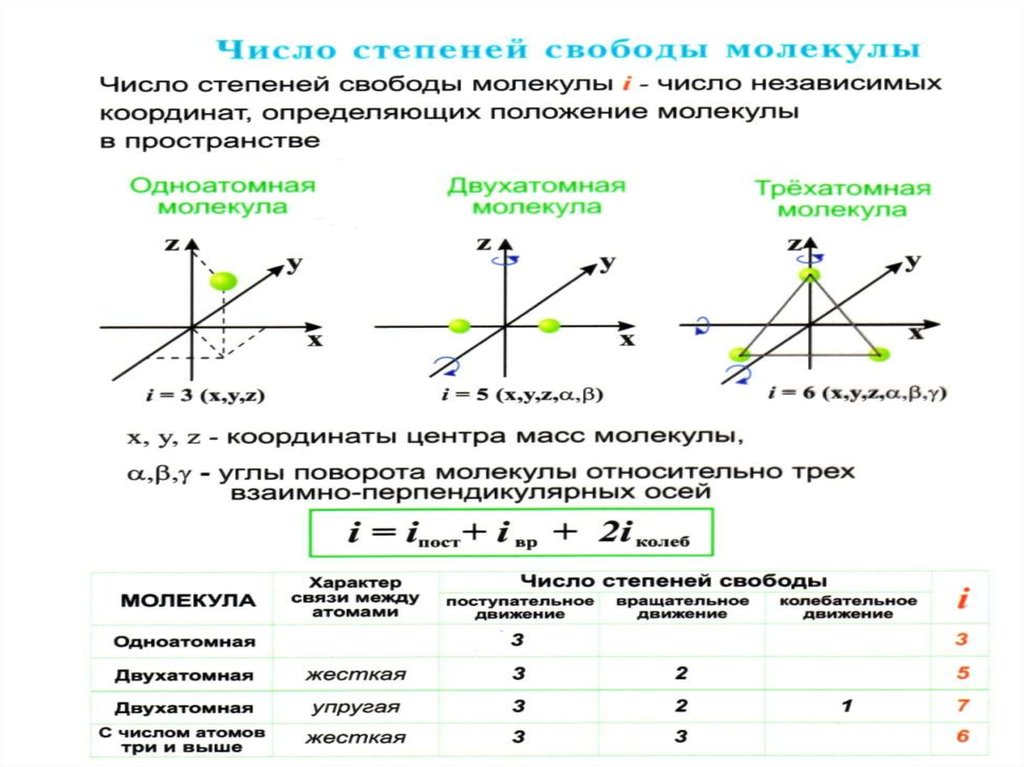
Число степеней свободыЧисло
независимых
координат,
определяющих конфигурацию и положение
системы
(атома
или
молекулы)
в
пространстве, называют числом степеней
свободы.
Одноатомный газ – система
невзаимодействующих материальных точек.
Атом обладает тремя
поступательными
степенями свободы.
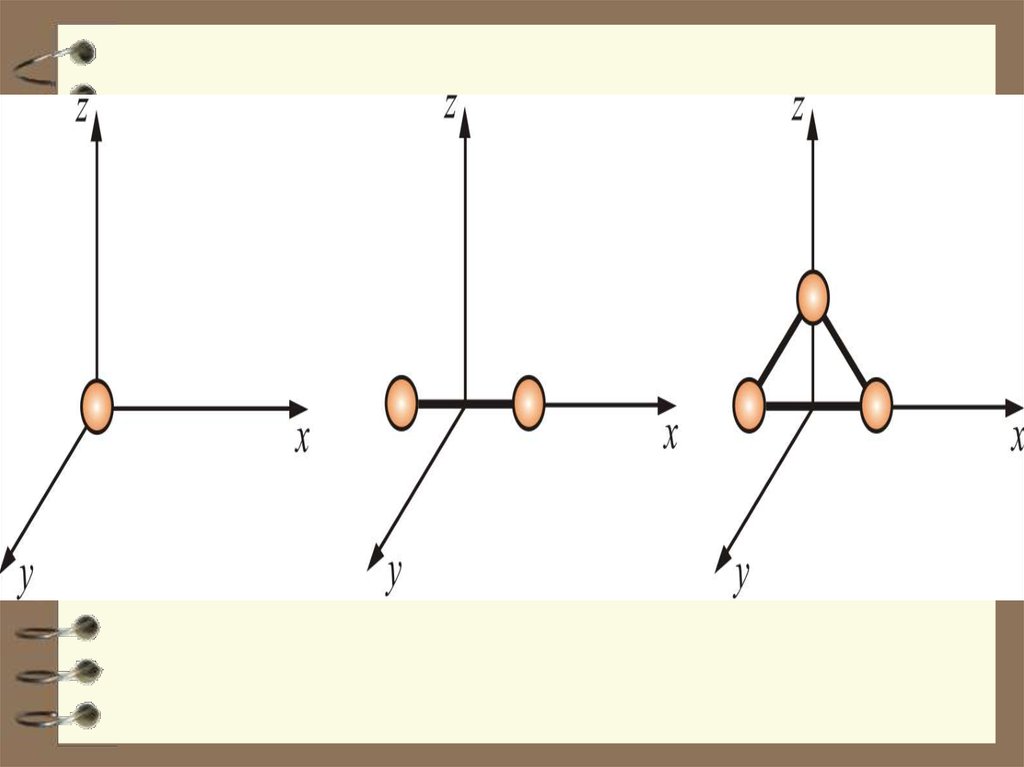
38. Числом степени свободы называется число независимых переменных, опреде-ляющих положение тела в пространстве и обозначается i i
Числом степени свободы называетсячисло независимых переменных, определяющих положение тела в пространстве
и обозначается i
i=3
Как видно, положение материальной
точки (одноатомной молекулы) задаётся
тремя координатами, поэтому она имеет
три степени свободы: i = 3
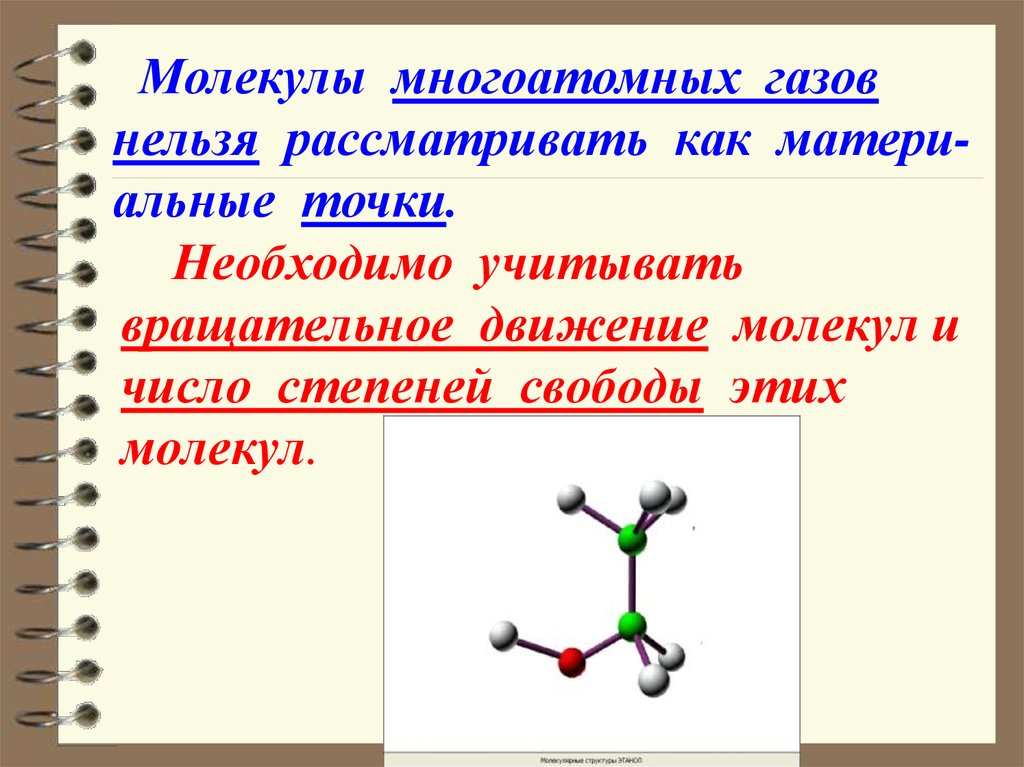
39. Необходимо учитывать вращательное движение молекул и число степеней свободы этих молекул.
Молекулы многоатомных газовнельзя рассматривать как материальные точки.
Необходимо учитывать
вращательное движение молекул и
число степеней свободы этих
молекул.
40. Многоатомная молекула может ещё и вращаться. Например, у двухатомных молекул вращательное движение можно разложить на два
независимых вращения, а любоевращение можно разложить на три
вращательных
движения
вокруг
взаимно перпендикулярных осей. Но
для двухатомных молекул вращение
вокруг оси x не изменит её положение в
пространстве,
а
момент
инерции
относительно этой оси равен нулю.
41.
42.
Двухатомная молекула, состоящая изжестко связанных атомов, обладает
тремя поступательными (центр масс) и
двумя вращательными степенями свободы. Вращение вокруг оси z молекулы не меняет её положения.
43.
Трехатомная (многоатомная) молекула, состоящая из жестко связанныхатомов, обладает тремя поступательными (центр масс) и тремя вращательными степенями свободы i = 6.
Если возможны колебания атомов,
то добавляется колебательная
степень свободы.
i iпост iвращ 2iколеб
44.
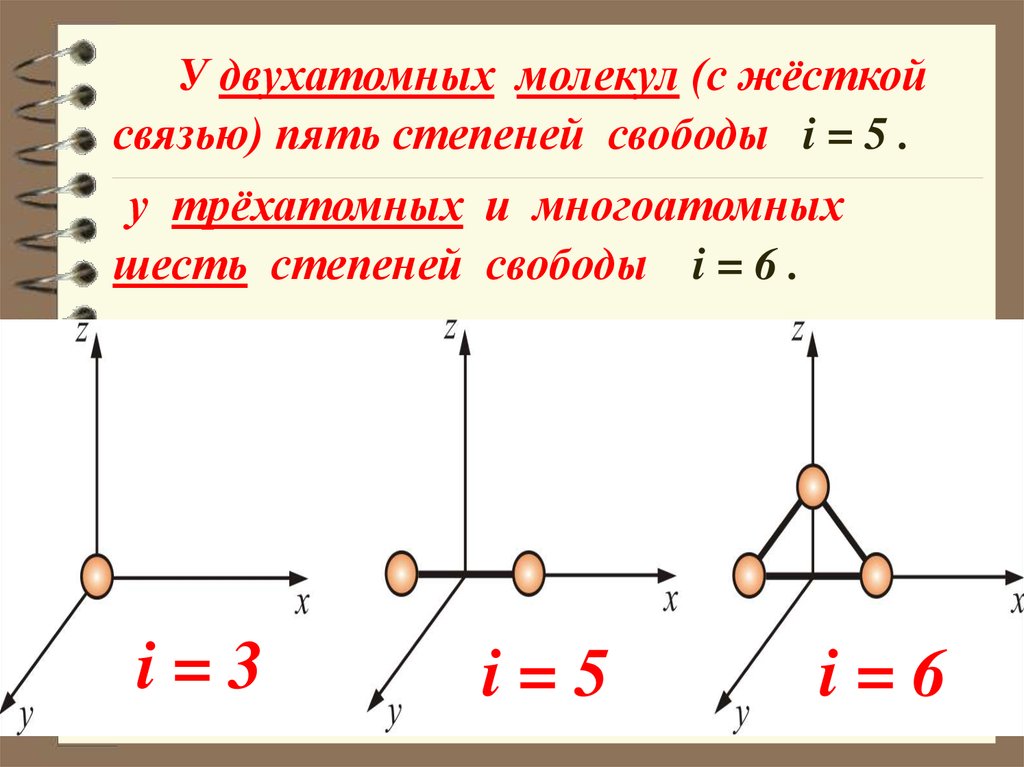
У двухатомных молекул (с жёсткойсвязью) пять степеней свободы i = 5 .
у трёхатомных и многоатомных
шесть степеней свободы i = 6 .
i=3
i=5
i=6
45.
46. При взаимных столкновениях молекул возможен обмен их энергиями и превращение энергии вращательного движения в энергию
поступательногодвижения
и
обратно. Таким путём установили
равновесие
между
значениями
средних энергий поступательного и
вращательного движения молекул.
47.
Средняя энергия поступательного3
движения молекулы равна: Е kT
2
Независимо от общего числа степеней
свободы молекул три степени свободы
всегда поступательные. Ни одна из
поступательных степеней свободы не
имеет преимущества перед другими,
поэтому на каждую из них приходится
в среднем одинаковая энергия, равная
Е 1
1/3 значения Е, т.е.
Е1
3
2
kT
48. Больцман доказал, что, средняя энергия приходящаяся на одну степень свободы равна:
Закон о равномерном распределенииэнергии по
степеням свободы
Больцман доказал, что, средняя
энергия
Е
приходящаяся на одну степень
свободы равна:
1
kT
2
49.
В классической статистической физикевыводится закон Больцмана о равномерном распределении энергии по степеням
свободы молекул: для статистической
системы, находящейся в состоянии
термодинамического равновесия, на каждую
поступательную и вращательную степени
свободы приходится в среднем кинетическая
энергия, равная kT / 2 , а на каждую колебательную степень свободы - в среднем
энергия, равная kT .
50.
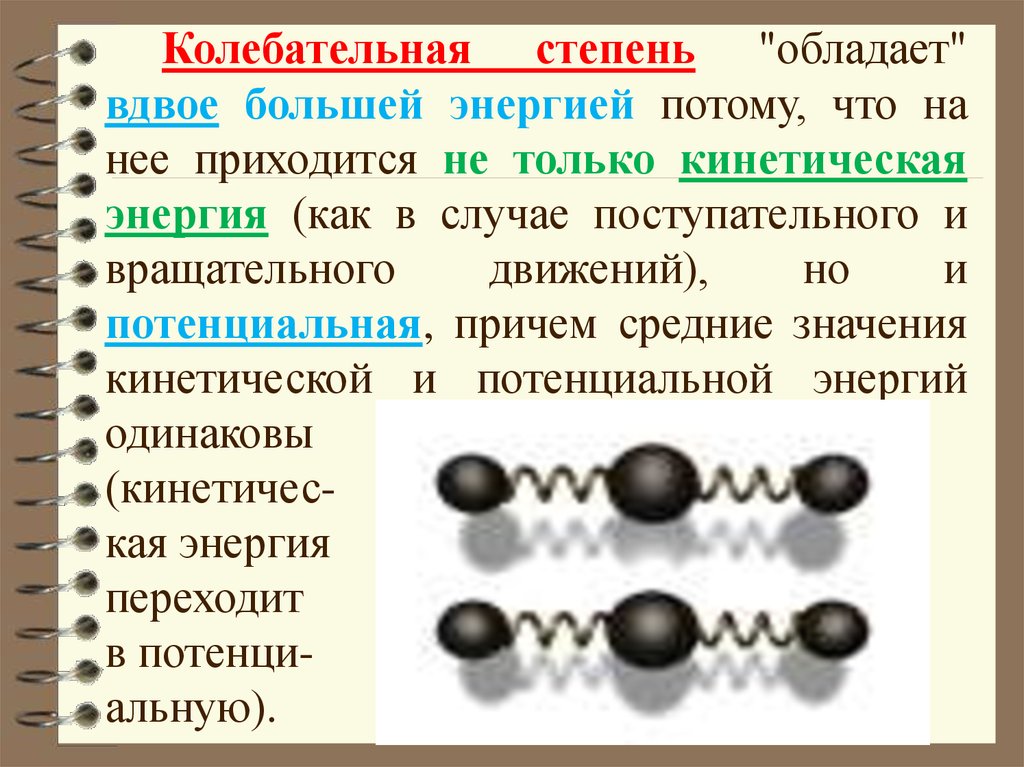
Колебательная степень "обладает"вдвое большей энергией потому, что на
нее приходится не только кинетическая
энергия (как в случае поступательного и
вращательного
движений),
но
и
потенциальная, причем средние значения
кинетической и потенциальной энергий
одинаковы
(кинетическая энергия
переходит
в потенциальную).
51.
Итак, средняя энергияприходящаяся на одну степень
свободы:
1
Е kT
2
52. У одноатомной молекулы i = 3, тогда для двухатомных молекул i = 5 для трёхатомных молекул i = 6
У одноатомной молекулы i = 3, тогда3
Е kT ,
2
для двухатомных молекул i = 5
5
Е kT ,
2
для трёхатомных молекул i = 6
6
Е kT .
2
53. На среднюю кинетическую энер-гию молекулы, имеющей i-степеней свободы приходится Это и есть закон Больцмана о равномерном
На среднюю кинетическую энергию молекулы, имеющей i-степенейсвободы приходится
i
Е kT
2
Это и есть закон Больцмана о
равномерном распределении средней
кинетической энергии по степеням
свободы. Здесь
i = iпост + iвращ + 2iкол
54. Теплоёмкости одноатомных и многоатомных газов
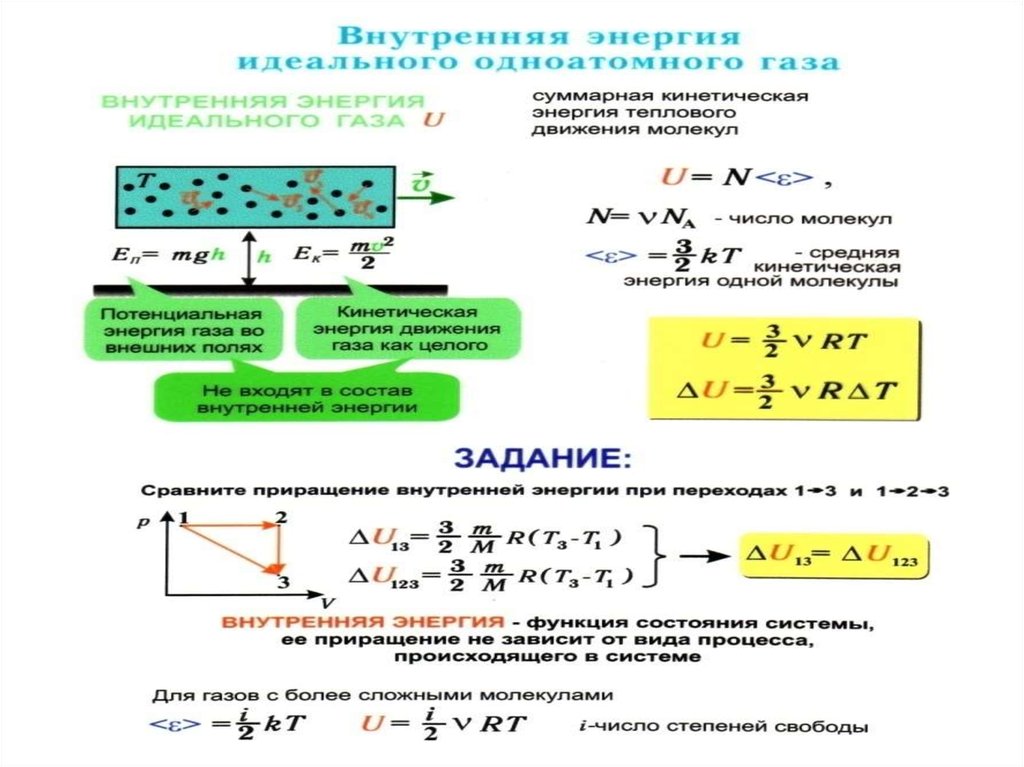
Внутренняя энергия одного моляодноатомного идеального газа равна
3
3
U N A kT RT
2
2
3
U RT
2
3
Дж
dU
CV
R 12,5
моль К
dT V 2
55.
Джмоль К
хорошо подтверждается на
опыте с He, Ne, Ar, Kr,
парами одноатомных газов.
То, что C 12,5
V
,
56.
Внутренняя энергия одного моляидеального газа c i степенями
свободы равна:
U
i
RT
2
i
dU
CV
R
2
dT V
молярная
теплоёмкость
при
постоянном объеме СV – величина
постоянная, от температуры не зависит.
57.
58.
Для одного моля идеального газа с i степенями свободы теплоёмкость C P :i
i 2
CP R R
R
2
2
Постоянная адиабаты (коэффициент
Пуассона) для идеального
СР i 2
газа:
СV
i
Для одноатомного идеального газа (i = 3): 20,8
12,5
1,67
59. для трех и более атомных молекул:
При этом: для двухатомных молекул:5
Дж
CV R 20,8
2
моль К
7
Дж
CP
CP R 29,1
;
1,4
2
моль К
CV
для трех и более атомных молекул:
6
Дж
CV R 3R 24,9
2
моль К
8
Дж
4
C Р R 4 R 33,3
; 1,33
2
моль К
3
60.
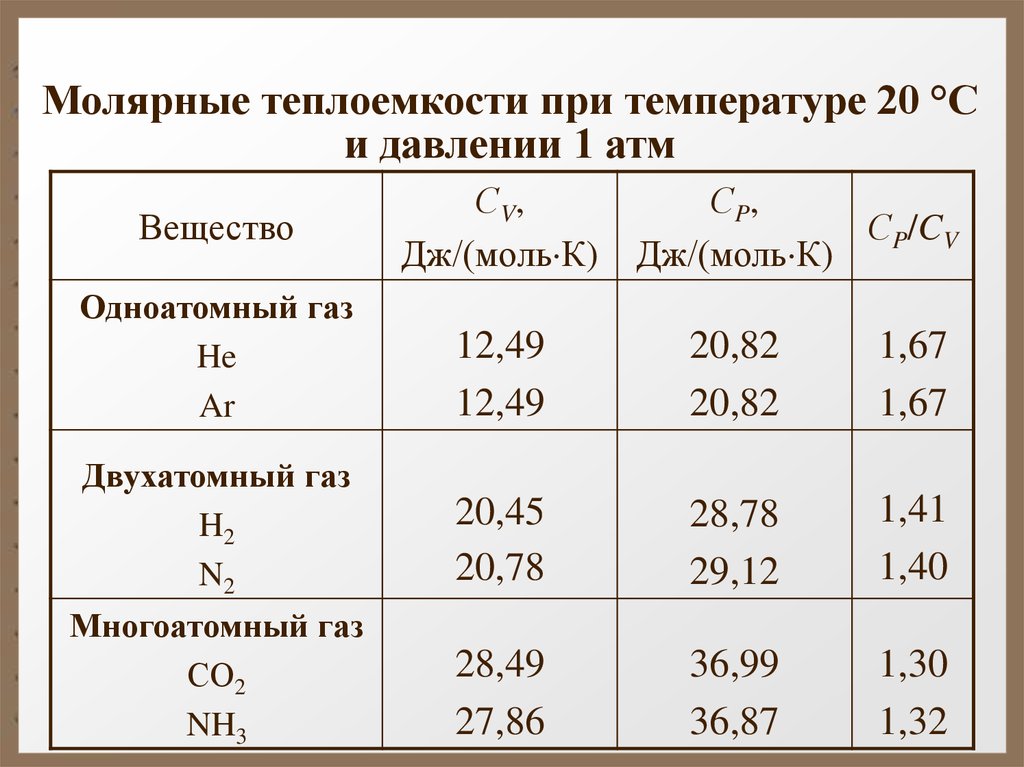
Молярные теплоемкости при температуре 20 °Си давлении 1 атм
Вещество
С V,
Дж/(моль К)
С P,
СP/CV
Дж/(моль К)
Одноатомный газ
He
Ar
12,49
12,49
20,82
20,82
1,67
1,67
Двухатомный газ
H2
N2
20,45
20,78
28,78
29,12
1,41
1,40
Многоатомный газ
СО2
NH3
28,49
27,86
36,99
36,87
1,30
1,32
61. В общем случае, для молярной массы газа
iCV R
2
i
i 2
CP CV R R R
R
2
2
i 2
CP
R
2
62. Для произвольного количества газов ( для ν молей ): Из теории также следует, что СV не зависит от температуры (рисунок).
Для произвольного количествагазов ( для ν молей ):
i m i
CV R R
2 2
i 2 m i 2
CP
R
R
2
2
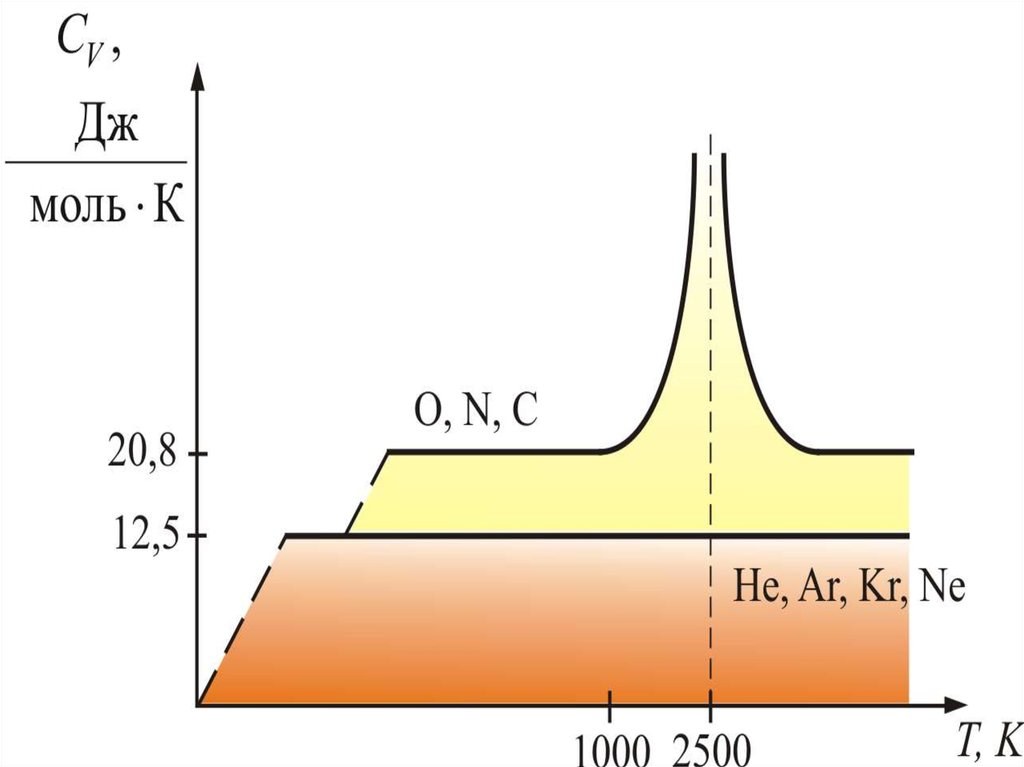
Из теории также следует, что СV не
зависит от температуры (рисунок).
63.
64. Для одноатомных газов это выполняется в очень широких пределах, а для двухатомных газов только в интервале от 100 1000 К.
Для одноатомных газов этовыполняется в очень широких
пределах, а для двухатомных газов
только в интервале от 100 1000 К.
Отличие связано с проявлением
квантовых законов. При низких
температурах
колебательное
движение как бы «заморожено» и
двухатомные молекулы движутся
поступательно, как одноатомные и
равны
их
теплоёмкости.
65.
При увеличении температуры, когдаТ > 1000 К, начинают сказываться
колебания атомов молекулы вдоль
оси z (атомы в молекуле связаны не
жёстко, а как бы на пружине).
66. Одна колебательная степень свободы несет энергии, так как при этом есть и кине-тическая и потенциальная энергия, то есть
Одна колебательная степень свободы несет1
kT энергии, так как при этом есть и кине2
тическая и потенциальная энергия, то есть
появляется шестая степень свободы – колебательная. При температуре равной 2500 К,
молекулы диссоциируют. На диссоциацию
молекул тратится энергия раз в десять превышающая среднюю энергию поступательного движения. Это объясняет сравнительно низкую температуру пламени. Кроме того, атом – сложная система, и при высоких
температурах начинает сказываться движение электронов внутри него.
67.
68.
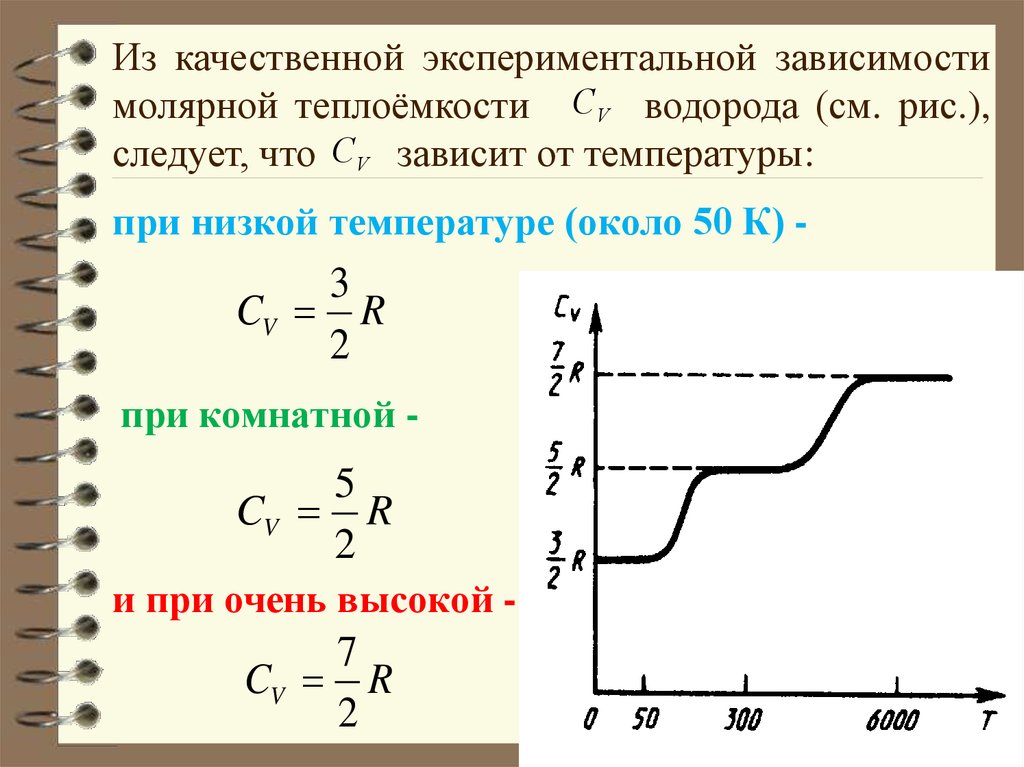
Из качественной экспериментальной зависимостимолярной теплоёмкости CV водорода (см. рис.),
следует, что CV зависит от температуры:
при низкой температуре (около 50 К) -
3
CV R
2
при комнатной -
5
CV R
2
и при очень высокой -
7
CV R
2
69.
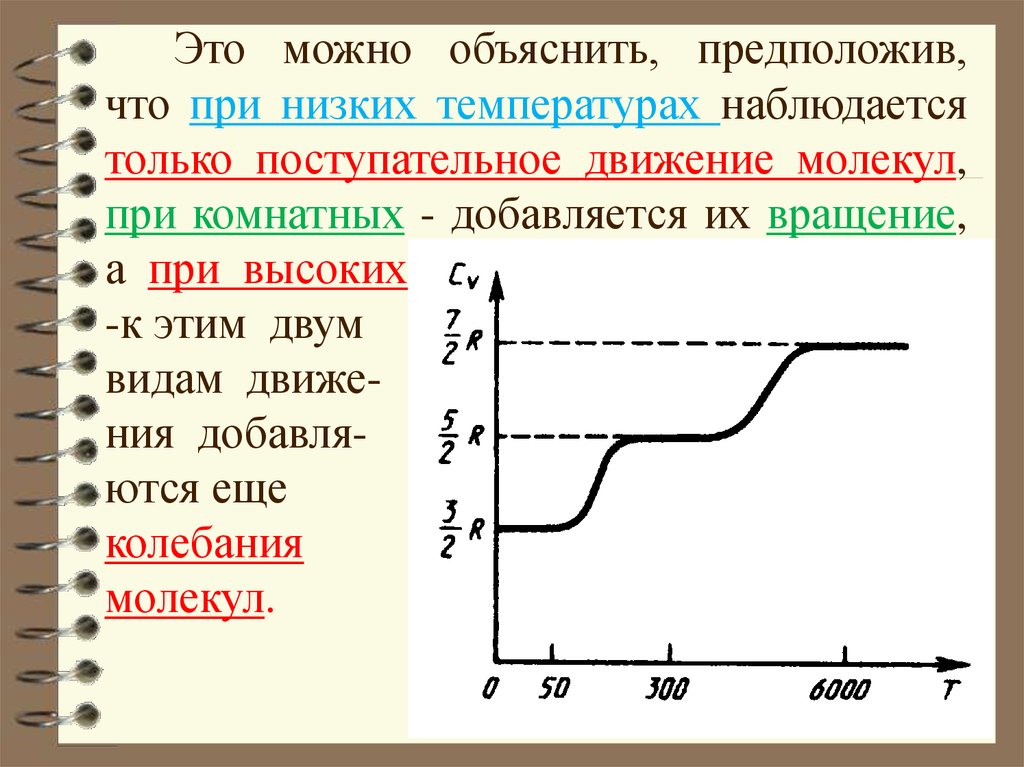
Это можно объяснить, предположив,что при низких температурах наблюдается
только поступательное движение молекул,
при комнатных - добавляется их вращение,
а при высоких
-к этим двум
видам движения добавляются еще
колебания
молекул.
70.
Расхождение теории и экспериментанетрудно объяснить. Дело в том, что при
вычислении теплоёмкости надо учитывать
квантование энергии вращения и
колебаний молекул (возможны не любые
вращательные и колебательные энергии, а
лишь определенный дискретный ряд
значений энергий). Если энергия теплового
движения недостаточна, например, для
возбуждения колебаний, то эти колебания
не вносят своего вклада в теплоёмкость
(соответствующая
степень
свободы
"замораживается"-
71.
-кней
не
применим
закон
равнораспределения
энергии).
Этим
объясняется, что теплоемкость моля
двухатомного газа – водорода - при
комнатной температуре равна 5R / 2 ,
вместо 7R / 2 при высоких температурах.
Аналогично можно объяснить уменьшение
теплоёмкости при низкой температуре
("замораживаются" вращательные степени
свободы) и увеличение при высокой
("возбуждаются" колебательные степени
свободы).






















































 Физика
Физика








