Похожие презентации:
Молекулярная физика и термодинамика
1. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
2. Молекулярная физика
Молекулярная физика-раздел физики изучающий строение и свойства вещества, исходя из молекулярнокинетических представлений основывающихся натом , что все тела состоят из молекул, находящихся в
непрерывном, хаотическом движении.
Процессы изучаемые молекулярной физикой являются
результатом совокупного действия огромного числа
молекул. Законы поведения большого числа молекул
изучаются на основе статистического метода основанного на том, что свойства макроскопической системы определяются свойствами частиц системы, особенностями их движения и усреднёнными значениями динамических характеристик этих частиц.
3. Термодинамика
Термодинамика-раздел физики, изучающий свойствамакроскопических систем, находящихся в состоянии
термодинамического равновесия, и процессы перехода между этими состояниями. Термодинамика не
рассматривает микропроцессы, которые лежат в
основе этих превращений. Этим термодинамический
метод отличается от статистического.
Термодинамика имеет дело с термодинамической системой (совокупностью макроскопических тел, которые взаимодействуют друг с другом или с другими
телами (внешней средой)). Основа термодинамического метода - определение состояния термодинамической системы. (Аналогия с методом «черного
ящика»).
4.
Состояние системы задаётся термодинамическими параметрами (параметрами состояния) - совокупностьюфизических величин, характеризующих свойства термодинамической системы. В качестве параметров
используют: давление P, температуру T, объем V и др.
• Температура- физическая величина, характеризующая
степень нагретости макроскопической системы
в
состоянии термодинамического равновесия (система
находится в термодинамическом равновесии, если её
состояние с течением времени не изменяется. Единицы
измерения: кельвин К и градус Цельсия ⁰С и др.
В качестве реперной точки термодинамической температурной шкала используется тройная точка воды .
5.
Тройная точка воды определяет состояние, когда триее фазы (вода, пар и лёд) находятся в термодинамическом равновесии ( давление Р = 609 Па, температура Т=273,15 К).
• Удельный объём v- объём единицы массы. Когда тело однородно (его плотность ρ=const), то V m 1 .
При постоянной массе удельный объём пропорционален общему объёму V и макроскопические свойства тела можно охарактеризовать объёмом тела V.
• Давление Р- физическая величина, численно равная
силе, действующей на единицу площади поверхности тела по направлению нормали к этой поверхdF
ности.
P n
dS
6. Молекулярно-кинетическая теория идеальных газов (МКТ)
7. ИДЕАЛЬНЫЙ ГАЗ
В МКТ пользуются идеализированной модельюидеального газа согласно которой:
• Собственный объём молекул газа пренебрежимо
мал по сравнению с объёмом сосуда.
• Молекулы не взаимодействуют между собой.
• Молекулы (частицы) сталкиваются по законам соударения абсолютно упругих тел.
Наиболее близко под условия идеального газа подходит любой разряженный газ.
8. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА (УРАВНЕНИЕ МЕНДЕЛЕЕВА-КЛАПЕЙРОНА)
Опытным путём, ещё до составления МКТ, был установлен ряд законов, описывающих поведениеидеальных газов:
• Закон Бойля-Мариотта
• Закон Гей-Люсака
• Закон Шарля
• Закон Авогадро
• Закон Дальтона
9. Закон Бойля-Мариотта
ИзотермаT const PV const
m const
Т – температура газа (в Кельвинах)
m – масса газа
V – объём занимаемый газом
Р – давление газа
10. Закон Гей-Люсака
Ð constT
V V0 (1 t ), V V0T V0
T0
m const
Закон Шарля
V const
T
P P0 (1 t ), P P0
T0
m const
Т – термодинамическая температура,
t – температура по шкале Цельсия,
P₀,V₀ - давление и объём газа при Т0=273,15 К,
1
K 1 - коэффициент объемного расширения.
273,15
11.
T t1
t 273,15
Изобара
Изохора
P const V1 T1
m const
V2 T2
V const P1 T1
m const
P2 T2
V1=const
P
P1=const
V
V2=const
P2=const
V2 >V1
P2 >P1
-1̸α
0
t,˚C
-1̸α
0
0
1̸α
t,˚C
T, K
12. Закон Авогадро
Моли любых газов при одинаковых температуре идавлении занимают одинаковые объёмы. При
нормальных условиях этот объём равен :
V ì 22.41 10 3 ì
3
ìîëü
В одном моле различных веществ содержится одно
и тоже число молекул, называемое : постоянная
Авогадро.
N a 6,022 10 23 ìîëü
1
13. Закон Дальтона
Давление смеси идеальных газов равно суммепарциальных давлений входящих в неё газов.
Р Р1 Р2 Р3 Рп
Р₁,Р₂,Р₃,…,Рn – парциальные давления газов ( давления, которые оказывали бы газы смеси, если бы
они занимали объём равный объёму смеси при
той же температуре).
14. Уравнение Клапейрона
Состояние некоторой массы газа m определяется тремя параметрами: давлением Р объёмом V и температурой Т. Между этими параметрами существуетсвязь называемая уравнением состояния : f(P,V,T)=0.
где каждая из переменных является функцией двух
других.
Французский физик Клапейрон (1799-1864), соединив
уравнения Бойля-Мариотта и Гей-Люсака, вывел
уравнение состояния идеального газа:
PV
const
T
15. Молярная газовая постоянная
Д. И. Менделеев объединил уравнение Клапейрона изакон Авогадро, отнеся уравнение Клапейрона к одному молю вещества, использовав молярный объём
Vm . Согласно закону Авогадро, при одинаковых Р и m
моли всех газов занимают одинаковый объём Vm, и
общая для всех газов постоянная R - молярная газовая постоянная.
Числовое значение R определяется из уравнения состояния идеального газа, полагая что 1 моль вещества
находится при нормальных условиях:
P0 1,013 10 5 ( Ïà )
Äæ
R 8,31(
)
Ò0 273,15( Ê )
ìîëü Ê
3
3
V
22
,
41
10
(
ì
ìîëü )
m
16. Уравнение Менделеева-Клапейрона
PVm RTУравнение состояния идеального газа для одного моля
вещества.
От данного уравнения можно перейти к уравнению
Менделеева-Клапейрона для произвольной массы газа. Если 1 моль занимает объём Vm , то газ массой m,
при тех же условиях , займёт объём V m M Vm , где
М-молярная масса (масса 1 моля вещества (кг/моль)) .
m
PV
RT RT
M
m
M
- количество вещества.
17.
Часто используется иная форма записи уравнения состояния идеального газа с использованием постояннойБольцмана k.
R
23
k
1,38 10 ( Äæ Ê )
Na
RT kNaT
P
nkT
Vm
Vm
Na
N - концентрация молекул
n
Vm
V
При одинаковых температуре и давлении все газы содержат в единице объёма одинаковое число молекул.
Число молекул содержащееся в 1 м3 газа при нормальных условиях определяется числом Лошмита.
P0
Nl
2,68 10 25 ( ì
kT0
3
)
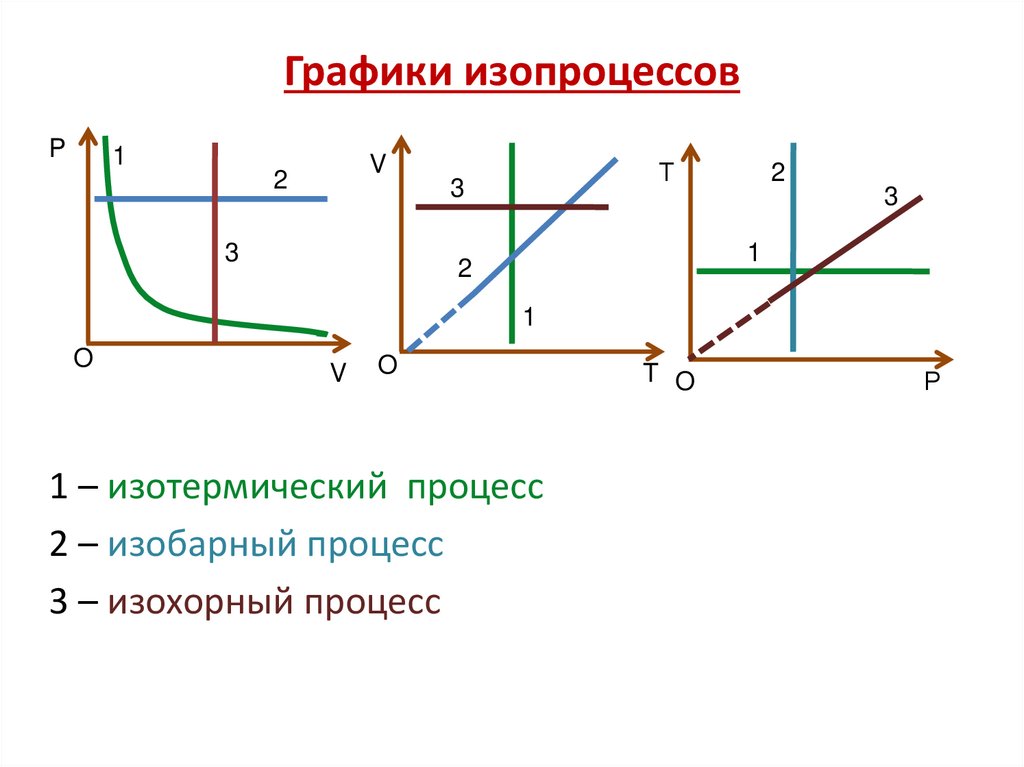
18. Графики изопроцессов
P1
V
2
Т
3
3
2
3
1
2
1
O
V
O
1 – изотермический процесс
2 – изобарный процесс
3 – изохорный процесс
T O
Р
19. Основное уравнение молекулярно-кинетической теории идеальных газов
20.
Для вывода основного уравнения молекулярно-кинетической теории (ОУМКТ) идеальных газов рассмотрим одноатомный идеальный газ. Газ заключён в сосуд с абсолютно упругими стенками. Молекулы газадвигаются хаотически, число столкновений между
молекулами пренебрежимо мало по сравнению с
ударами об стенки.
∆S
Выделим на стенке сосуда элементарную
v∆t
площадку ∆S и определим давление на
неё. При каждом соударении каждая молекула, движущаяся перпендикулярно площадке, передаёт ей
импульс m0 v ( m0 v) 2m0 v . Где:
m₀- масса молекулы
v – скорость молекулы
21.
За время ∆t площадки ∆S достигнут только те молекулыкоторые заключены в объёме цилиндра с основанием ∆S, и высотой v∆t . Число этих молекул n Sv t где
n-концентрация молекул.
Молекулы двигаются под разными углами и имеют
разные скорости, (причём скорости молекул при
соударении меняются). Для упрощения хаотическое
движение молекул заменяют на движение вдоль 3
взаимно перпендикулярных направлений. Вдоль
каждого двигается треть от общего числа молекул,
причём половина (⅙ часть от всех молекул)в одну
сторону, а половина в другую. Тогда число ударов в
заданном направлении будет 1 n Sv t .
6
22.
При столкновении с площадкой эти молекулы передадут ей импульс:1
1
p 2m0 v n Sv t m0 nv 2 S t
6
3
Тогда давление газа на стенку сосуда будет:
P
p
1
nm0 v 2
t S
3
Если газ в объёме V содержит N молекул двигающихся
со скоростями v₁,v₂,v₃,…,vn то целесообразно рассматривать среднюю квадратичную скорость v кв характеризующую всю совокупность молекул газа.
v кв
1
N
N
2
v
i
i 1
23. Основное уравнение МКТ
Тогда уравнение давления примет вид:1
P nm0 v кв
3
2
Основное уравнение МКТ для идеального газа
Учитывая что n=N/V, можно выразить:
1
PV Nm0 v кв
3
2
2 m0 v кв
N
3
2
2
2
E
3
Е –суммарная кинетическая энергия поступательного
движения всех молекул.
24. Средние значения скорости и энергии
12
Так как масса всего газа m Nm0, и PV m v кв ,
3
1
2
то для 1 моля газа PVm M vêâ RT , следовательно:
3
vкв
3RT
M
3RT
m0 N a
3kT
m0
Значение средней квадратичной скорости молекул газа
Аналогично:
E m0 v 2 3
0
kT
N
2
2
Средняя кинетическая энергия поступательного движения одной молекулы идеального газа.
25. Закон Максвелла для распределения молекул идеального газа по скоростям и энергиям теплового движения
26.
При выводе основного уравнения МКТ молекулам задавали различные скорости. В результате многократных соударений скорость каждой молекулы меняется по модулю и направлению. Однако, из-за хаотического движения молекул, все направления движения считаются равновероятными, то есть в любом направлении движетсяпримерно одинаковое количество молекул. По МКТ, в
газе, находящемся в состоянии равновесия, при постоянной температуре, как бы не изменялись отдельные
скорости молекул при столкновениях, среднеквадратичная скорость
vêâ молекул массой m₀ остаётся постоянной. Значит, в газе находящемся в равновесии,
устанавливается некоторое стационарное, не изменяющееся со временем, распределение молекул по скоростям, подчиняющееся определённому статистическому закону. Этот закон был выведен Максвеллом.
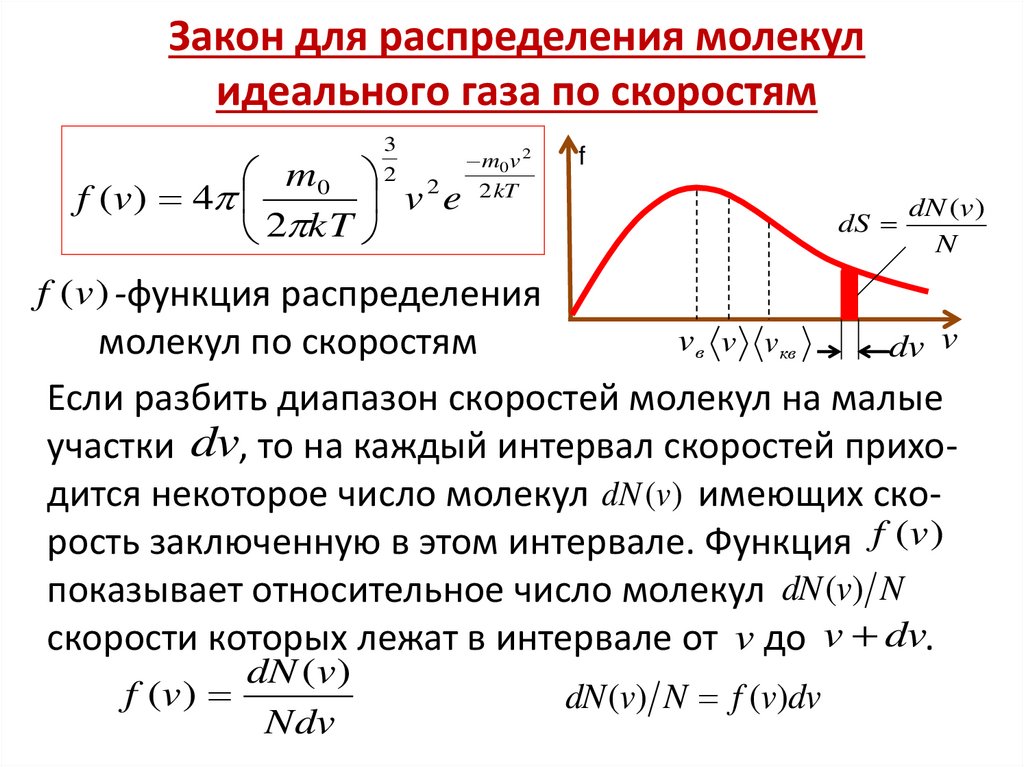
27. Закон для распределения молекул идеального газа по скоростям
32
m0 2
f (v) 4
v e
2 kT
m0 v 2
2 kT
f
dS
dN (v)
N
f (v ) -функция распределения
vв v v кв
молекул по скоростям
dv v
Если разбить диапазон скоростей молекул на малые
участки dv, то на каждый интервал скоростей приходится некоторое число молекул dN (v) имеющих скорость заключенную в этом интервале. Функция f (v )
показывает относительное число молекул dN (v) N
скорости которых лежат в интервале от v до v dv.
dN (v )
f (v )
Ndv
dN (v) N f (v)dv
28.
Конкретный вид функции зависит от природы газа (массы молекул ), и параметра состояния (температуры).m0 v 2
При возрастании скорости v множитель
e 2 kT
уменьшается быстрее, чем растёт множитель v 2 и функция f (v ), начинаясь от нуля, достигает максимума при
Т1<Т2
vв и асимптотически стремится
f
к нулю. Кривая не симметрична
относительно vв.
При повышении температуры гаv
за максимум распределения функции по скоростям сместится вправо, однако площадь ограниченная кривой останется неизменной, и при росте температуры кривая
распрелеления молекул будет понижаться.
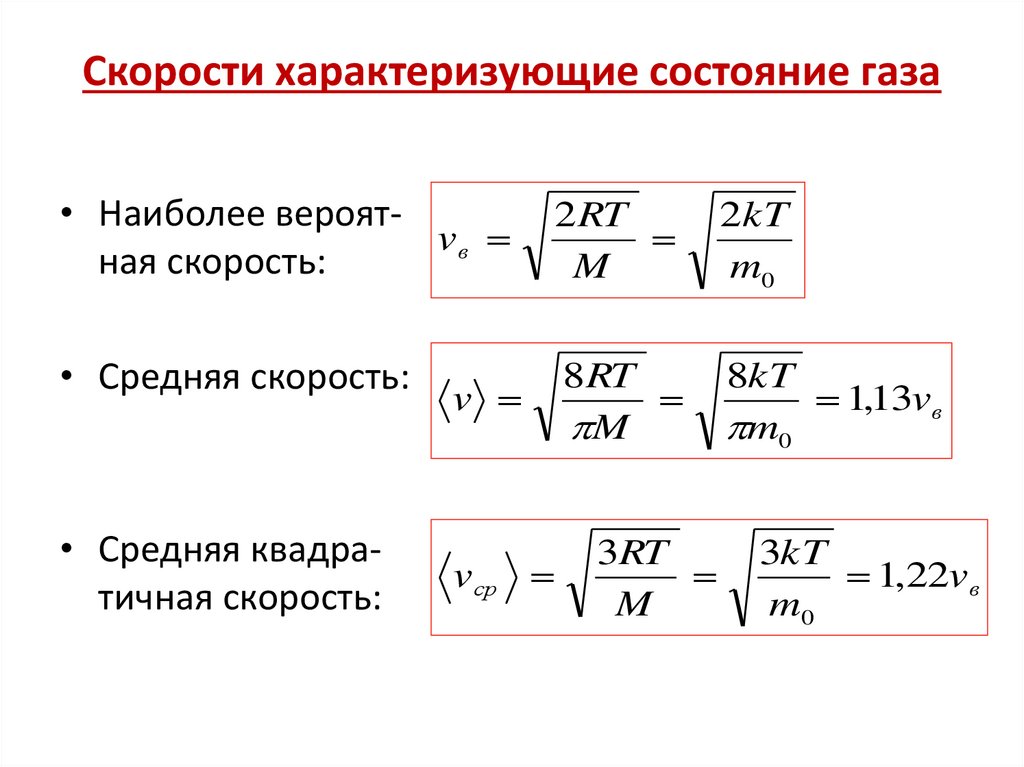
29. Скорости характеризующие состояние газа
• Наиболее вероятvвная скорость:
2 RT
M
2kT
m0
• Средняя скорость:
8RT
M
8kT
1,13vв
m0
• Средняя квадратичная скорость:
v
vср
3RT
M
3kT
1,22vв
m0
30. Функция распределения молекул по энергиям теплового движения
f ( )2
kT
3
2
1
2
e
kT
Функция распределения молекул по энергиям
Средняя кинетическая энергия одной молекулы
идеального газа:
f d
0
3
2
kT
0
2
3
2
e
kT
3
d kT
2
Полученный результат совпадает с полученным
ранее.
31. ФОРМУЛА БОЛЬЦМАНА ЭЛЕМЕНТЫ КЛАССИЧЕСКОЙ СТАТИСТИКИ (РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА-БОЛЬЦМАНА)
32.
Газы атмосферы находится в потенциальном поле тяготения Земли. Если бы не было:• Поля тяготения Земли: атмосферный воздух рассеялся бы по Вселенной.
• Теплового движения молекул: молекулы воздуха
упали бы на Землю.
Тяготение и тепловое движение приводят к стационарному состоянию газа, при котором происходит убыль
концентрации и давления газа с ростом высоты над
Землей.
Если газ (или другая система частиц) находится во внешнем потенциальном силовом поле, то распределение частиц по объёму описывается с помощью закона Больцмана.
33. Закон Больцмана
Если высота над Землей равна h , то давP2h
dh
ление Р , на высоте
давление:
P+dP
dh
P dP dh 0 dP 0 (давление с
P
высотой убывает).
h
Разность давлений Р и P dP равна весу газа, заключённого в объёме цилин- P1 h1
дра высотой dh с основанием, площадь которого равна единице площади. Значит:
h2
P P dP gdh
- плотность газа на высоте h ( при изменении высоты на dh плотность газа можно считать постоянной).
dP gdh
34. Барометрическая формула
Используя уравнение состояния идеального газа (УСИГ)m
m PM
PM
dP
gM
PV RT
dP
gdh
dh
M
V RT
RT
P
RT
При большом изменении высоты от h1 до h2 давление
меняется от Р1 до Р2 .
P2
dP
Mg
P P RT
1
h2
h1
P2
Mg
dh ln
(h2 h1 )
P1
RT
Р2 P1e Mg ( h2 h1 ) RT
Барометрическая формула – характеризует атмосферное давление в зависимости от высоты.
35.
h1 0 уровень моря, то:Если считать что
Mgh
RT
m0 gh
kT
P P0 e
где:
P - давление на высоте h
P0 - давление на уровне моря
Так как P nkT, значит:
n n0 e
Mgh
RT
n0 e
n0 e
En
kT
n 0 - концентрация молекул на уровне моря h 0
n - концентрация молекул на высоте h
E n m0 gh - потенциальная энергия в поле тяготения.
m0 - масса одной молекулы
36. Формула Больцмана
n n0 eEn
kT
Закон Больцмана устанавливает число частиц dn x, y, z ,
координаты которых находятся в интервале от x до
x dx , от y до y dy , от z до z dz .То есть dn x, y, z число молекул находящееся в элементарном объёме.
Распределение молекул газа по координатам и скоростям , при наличии произвольного потенциального
поля, описывают распределением Максвелла-Больцмана .
dn const
1
(2 mkT )
3
e
2
2 2
p2
x p y pz
2 m kT
dpx dp y dpz e
En x , y , z
kT
dxdydz
37.
dn -число молекул находящихся в шестимерном пространстве в элементе объёма d dxdydzdpx dp y dp zEn x, y, z -потенциальная энергия молекулы во внешнем силовом поле в точке с координатами x, y, z и
проекциями импульса по осям p x , p y , p z .
Закон Максвелла-Больцмана представляет собой произведение двух функций распределения, одна из них
расписывает распределение по координатам, дру-гая
по скоростям.
38. СРЕДНЕЕ ЧИСЛО СТОЛКНОВЕНИЙ СРЕДНЯЯ ДЛИНА СВОБОДНОГО ПРОБЕГА МОЛЕКУЛ
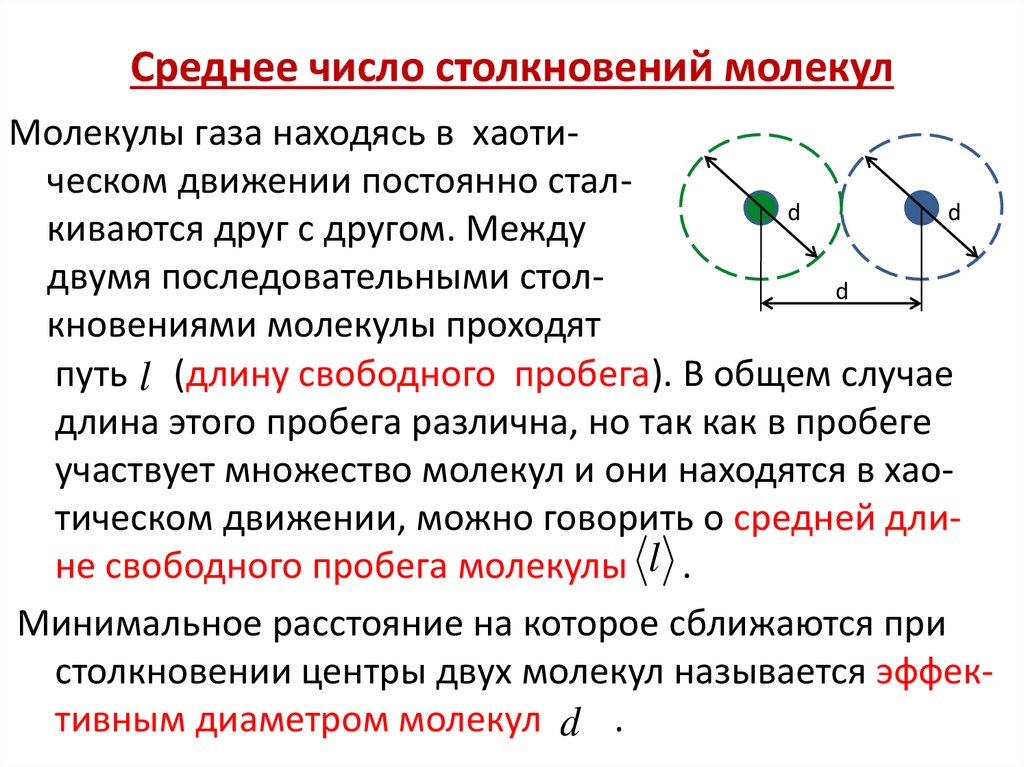
39. Среднее число столкновений молекул
Молекулы газа находясь в хаотическом движении постоянно сталdd
киваются друг с другом. Между
двумя последовательными столd
кновениями молекулы проходят
путь l (длину свободного пробега). В общем случае
длина этого пробега различна, но так как в пробеге
участвует множество молекул и они находятся в хаотическом движении, можно говорить о средней длине свободного пробега молекулы l .
Минимальное расстояние на которое сближаются при
столкновении центры двух молекул называется эффективным диаметром молекул d .
40.
Эффективный диаметр молекул зависит от скоростисталкивающихся молекул, от температуры газа (немного
растёт с ростом температуры).
В среднем за 1 секунду молекула проходит путь
равный средней арифметической скорости v ( v 1 ), и
если среднее число столкновений испытанное молекулой за 1 секунду z , то средняя длина свободного пробега:
v
l
z
41.
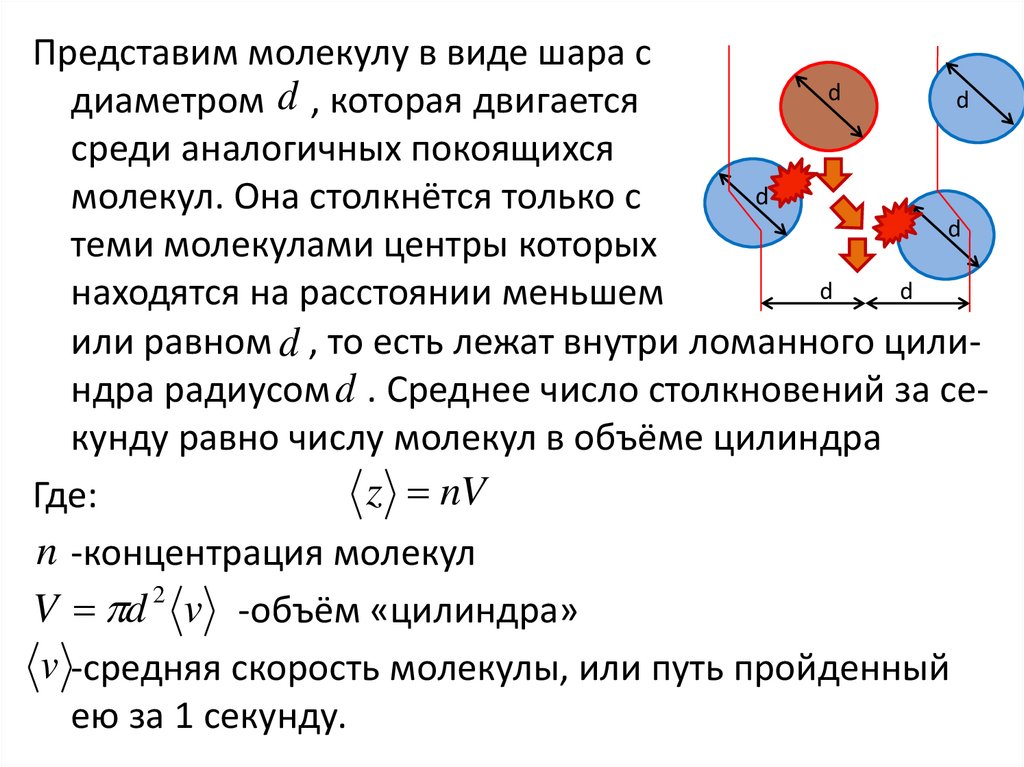
Представим молекулу в виде шара сd
d
диаметром d , которая двигается
среди аналогичных покоящихся
d
молекул. Она столкнётся только с
d
теми молекулами центры которых
d
d
находятся на расстоянии меньшем
или равном d , то есть лежат внутри ломанного цилиндра радиусом d . Среднее число столкновений за секунду равно числу молекул в объёме цилиндра
z nV
Где:
n -концентрация молекул
2
V d v -объём «цилиндра»
v -средняя скорость молекулы, или путь пройденный
ею за 1 секунду.
42.
Среднее число столкновений:z n d 2 v
Среднее число столкновений, с учётом движения других молекул:
z 2n d 2 v
Средняя длина свободного пробега молекул:
1
l
2
2n d
Значит l обратно пропорциональна концентрации молекул n . Так как Р nkT при постоянной температуре T концентрация молекул n пропорциональна
давлению Р и значит:
l1
n2 P2
l2
n1 P1
43. ЯВЛЕНИЯ ПЕРЕНОСА В ТЕРМОДИНАМИЧЕСКИ НЕРАВНОВЕСНЫХ СРЕДАХ
44.
В термодинамически неравновесных средах возникаютособые необратимые процессы называемые
явлениями переноса в результате которых происходит перенос энергии, массы, импульса. Это:
• Теплопроводность (перенос энергии)
• Диффузия (перенос массы)
• Внутреннее трение (перенос импульса)
Для простоты ограничимся одномерными явлениями
переноса.
45. Теплопроводность
Если в одной области газа кинетическая энергия больше чем вТ(Е )
другой, то, с течением времени,
вследствие постоянного столкновения молекул, происходит процесс выравнивания
средних кинетических энергий молекул (температур).
Перенос энергии в виде температур подчиняется
закону Фурье
к
dT
j E
dx
46.
j E - плотность теплового потока (величина определяемаяэнергией переносимой в форме теплоты в единицу
времени через единичную площадку перпендикулярную положительному направлению потока).
- теплопроводность (коэффициент теплопроводности).
dT
- градиент температуры равен скорости изменения
dx температуры на единицу длины х в направлении к
нормали к этой площадке.
При теплопроводности энергия переносится в направлении убывания температуры ( j E иdT dx противоположны по знаку). Теплопроводность численно равна
плотности теплового потока при градиенте температуры равной единице:
1
cV v l
3
47.
cV - удельная теплоёмкость газа при постоянном объёме.(количество теплоты необходимое для нагревания 1 кг газа на 1 К при постоянном объёме.- плотность газа
v -средняя скорость теплового движения молекул
l - средняя длина свободного пробега молекул
48. Диффузия
Диффузия - самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов,жидкостей или твёрдых тел.
Диффузия - обмен массой между телами.
Для однородного газа диффузия подчиняется
Закону Фика
d
jm D
dx
j m -плотность потока массы (величина определяемая
массой вещества диффундирующего в единицу времени через единичную площадку
перпендикулярную потоку.
49.
D -диффузия (коэффициент диффузии)d -градиент плотности равен скорости изменения
dx плотности на единицу длины х в направлении к нормали этой площадки. Перенос массы осуществляется
в направлении убывания плотности (знаки j m и d dx
противоположны).
Диффузия численно равна плотности потока массы при
градиенте плотности равном единице.
1
D v l
3
50. Вязкость. Внутреннее трение
v1<v2Вязкость (внутреннее трение)свойство жидкостей или газов
v1
v2
оказывать сопротивление перемещению одной части вещества
относительно другой.
При прохождении одних слоев жидкости (газа) относительно других , возникают силы внутреннего трения,
направленные по касательной к поверхности слоев.
Действие этих сил проявляется в том, что со стороны
слоя двигающегося медленнее, на слой двигающийся быстрее действует тормозящая сила. И наоборот
на слой двигающийся медленнее со стороны более
51.
быстрого слоя действует ускоряющая сила. Сила внутреннего трения тем больше, чем больше рассматриваемая поверхность и зависит от того, насколько быстроменяется скорость течения жидкости (газа) при переходе от слоя к слою. Пусть v2 v1 скорости слоев газа
(жидкости) и v v2 v1разница между скоростями
слоев . Направление в котором отсчитывается расстояние между слоями газа (жидкости) х перпендикулярно скоростям течения слоев жидкости.
Величина v x показывает как быстро меняется скорость при переходе от слоя к слою в направлении х
перпендикулярном направлению движения слоев и
называется градиентом скорости. Модуль сил внут v
реннего трения:
F
S
x
52.
-коэффициент пропорциональности, зависящий отприроды жидкости (газа) называется динамической
вязкостью . (Единица измерения Па с) равен динамической вязкости среды в которой при градиенте скорости с модулем равным 1 м/с на 1 м, возникает сила
1 Н на 1 м² поверхности касания слоев.
Чем больше вязкость, тем сильнее вещество отличается
от идеального, и тем большие силы внутреннего трения в них возникают. Вязкость зависит от температуры (у жидкостей с ростом температуры уменьшается,
у газов увеличивается).
Течение называется ламинарным если вдоль потока
каждый выделенный слой скользит относительно соседних не перемешиваясь с другими и турбулентным
если вдоль потока происходит перемешивание газа.
53.
Внутреннее трение подчиняетсяЗакону Ньютона
v
dv
F
S
j p
x
dx
j p -плотность потока импульса (величина определяемая
полным импульсом переносимым в единицу времени
в положительном направлении потока через единичную площадку перпендикулярную пути потока (импульс переносится в направлении убывания скорости,
знаки j p и dv dx противоположны)).
Динамическая вязкость численно равна плотности
потока импульса, при градиенте скорости равном 1:
1
v l
3
54.
Закономерности всех явлений переноса сходны междусобой, сходство их математических выражений обусловленно общностью процесса перемешивания молекул в процессе их хаотического движения и сталкивания между собой.
Коэффициенты , D, связаны между собой:
1
3 cV v l
D
1
D v l
1
3
cV
1
v l
3
55. ЗАКОНЫ ТЕРМОДИНАМИКИ
56. Термодинамическая система
Термодинамическая система- макроскопические объекты (тела и поля) которые могут обмениваться энергией как с друг другом так и со внешней средой, то естьс телами и полями, которые являются внешними по
отношению к данной системе.
Произвольная термодинамическая система находящаяся в любом термодинамическом состоянии обладает
полной энергией E складывающейся из: кинетичесм ех
кой энергии E к (энергии механического движения
как целого или её макроскопических частей), потенвн
E
циальной энергии п (во внешних силовых полях:
гравитационного, электромагнитного и т.д.), внутренней энергии U
E Е м ех Е вн U
к
п
57. Внутренняя энергия системы
Внутренней энергией тела (или системы тел) U называется энергия зависящая только от термодинамического состояния тела (системы) и включающая в себяэнергию всех видов внутреннего движения в системе
(теле) и энергию взаимодействия всех частиц (ионов,
атомов, молекул) входящих в тело (систему).
Внутренняя энергия совпадает с энергией покоя
системы.
58.
Например, внутренняя энергия газа,состоящего из многоатомных молекул, складывается из:• Кинетической энергии Eк теплового поступательного
и вращательного движения молекул.
• Кинетической Eк и потенциальной E п энергий колебаний атомов в молекулах.
• Потенциальной энергии E п обусловленной межмолекулярными взаимодействиями (не учитывается
для идеального газа).
• Энергии электронных оболочек атомов и ионов.
• Кинетической Eк и потенциальной E п энергий взаимодействия нуклонов в ядрах атомов.
59.
Внутренняя энергия является однозначной функциейтермодинамического состояния системы. Её значение не зависит от того, с помощью какого процесса
система пришла в данное состояние. Изменение U
при переходе системы из одного состояния 1 в другое 2 равно U U 2 U1 , и не зависит от вида процесса перехода из 1 в 2. Если система совершает круговой процесс, то полное изменение внутренней
энергии: dU 0
В идеальном газе молекулы между собой не взаимодействуют, следовательно внутренняя энергия будет
равна: U N
N - число молекул
i
kT -средняя энергия одной молекулы
2
60. Степени свободы
i степень свободы – число независимых переменных(координат) определяющих положение системы в
пространстве
z
Для материальной точки (молекулы) i 3 число
координат трёхмерного пространства (x,y,z)
x
y
Для двухатомного газа (совокупность 2 материальных точек, жестко связанных недеформи- z
рованной связью) i 5 (x,y,z-3 поступательx
ные, 2 –вращательные)
y
Для трёх- и многоатомных молекул i 6 (3z
поступательные, 3- вращательные
x
y
61.
Внутренняя энергия для 1 моля идеального газаi
i
U m kTN a RT
2
2
Внутренняя энергия для газа массой m
i m
i
U
kTN a RT
2M
2
Элементарное изменение внутренней энергии
i m
i
dU
kNa dT RdT
2M
2
62. Первое начало термодинамики
63.
Обмен энергией между термодинамическойсистемой и внешними телами происходит либо при
совершении работы, либо с помощью теплообмена.
• Количество энергии переданное системе внешними
телами путём теплообмена называется количеством
теплоты Q сообщенной системе.
• Количество энергии переданное системе внешними
телами при силовом взаимодействии между ними
называется работой А .
64.
Работой расширения называется работа, которую система производит против внешнего давления.Рассмотрим газ, находящийся под поршнем в цилиндрическом сосуде. Если газ расширяясь передвигает
поршень на бесконечно малое расстояние dl , это
значит, что он производит над ним работу:
S
А Fdl PSdl PdV
dl
dV
S -площадь поршня
Sdl dV-изменение объёма системы.
Полную работу совершаемую газом при изменении его
объёма от V1 до V2 найдём интегрированием:
V2
A PdV
V1
65.
Изменение внутренней энергии U12 закрытой системы(системы которая не может обмениваться веществом
с внешней средой), которое происходит при переходе
системы из состояния 1 в состояние 2 , равно сумме
совершенной над системой внешними
работы А12
силами и количества теплоты Q сообщаемого системе.
Q12
U12 A12
А12 А12 -
работа совершенная системой над
внешними телами в процессе 12.
66. Первое начало термодинамики
U Q AКоличество теплоты, сообщенное системе, расходу-ется
на изменение внутренней энергии и совер-шение
системой работы против внешних сил.
В дифференциальной форме уравнение имеет вид:
Q dU dA
dU -бесконечно малое изменение внутренней энергии
системы.
dA -элементарная работа
Q -бесконечно малое количество теплоты
Единицы измерения всех этих величин-Дж (джоули).





























































 Физика
Физика








