Похожие презентации:
Функции нескольких переменных. (Лекция 1)
1. Лекция №1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
1.2.
3.
4.
5.
6.
Определение функции нескольких переменных.
Предел и непрерывность.
Частные производные и полный дифференциал.
Производная сложной функции.
Производная неявной функции.
Частные производные и дифференциалы высших
порядков.
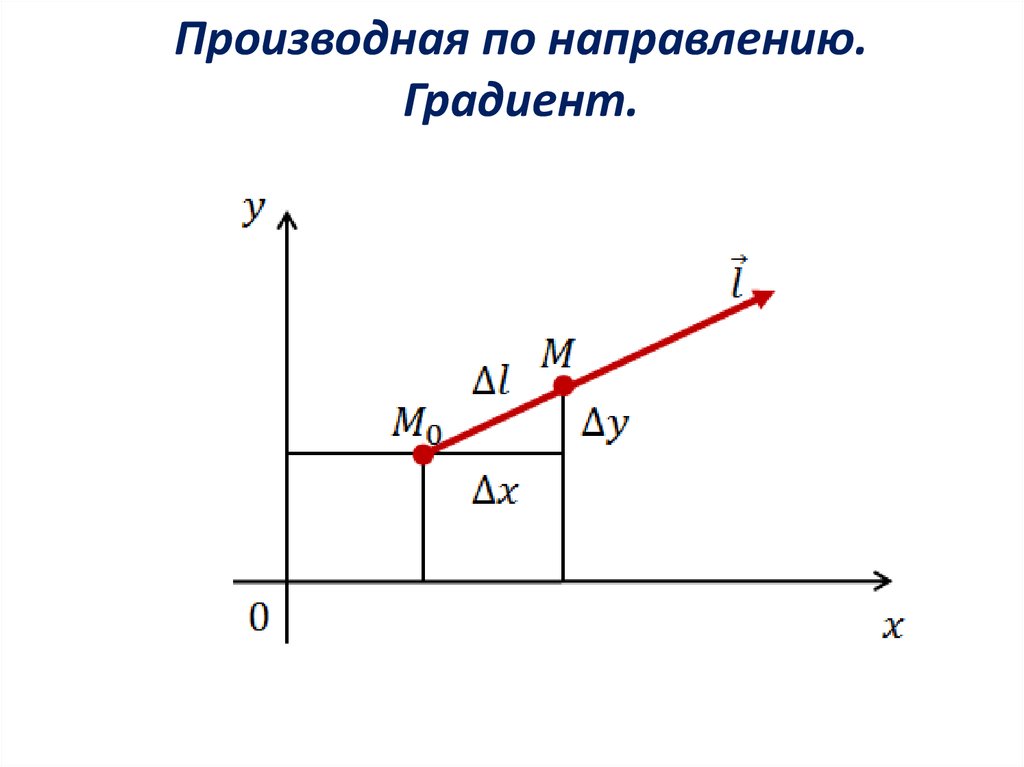
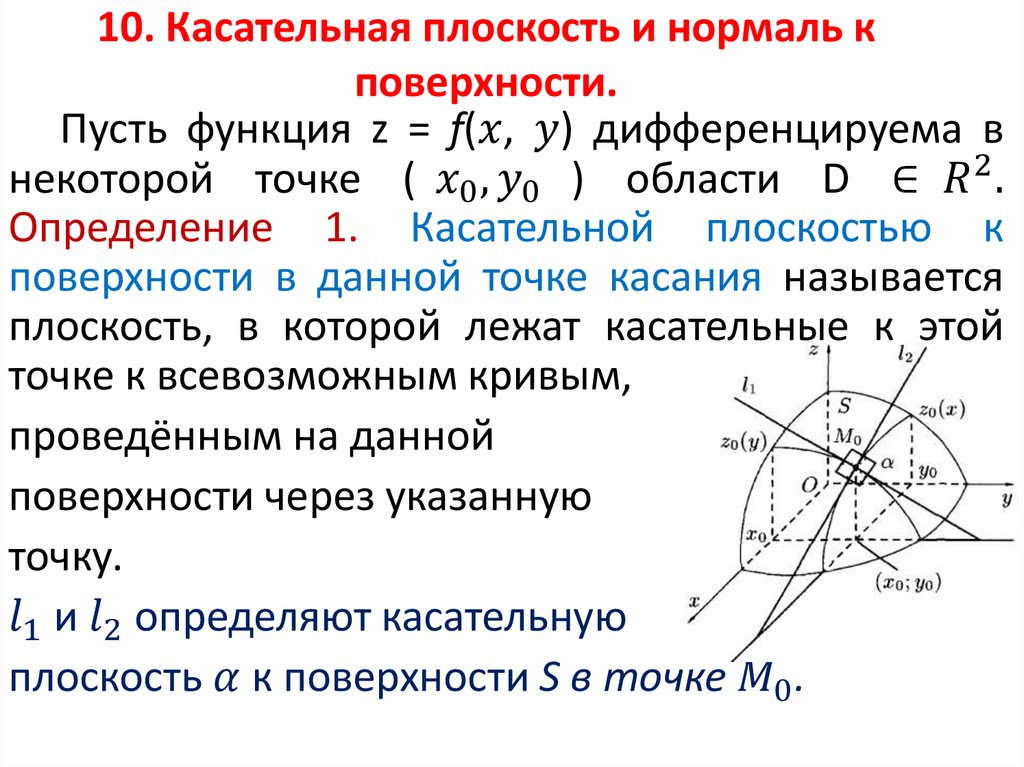
7. Производная по направлению и градиент.
8. Экстремумы функций двух переменных.
2. Литература
1. Д. Письменный «Конспект лекций повысшей математике», Ч.1, Ч.2.
2. Н.С. Пискунов «Дифференциальное и
интегральное исчисления», Т. 1, 2.
3. М.В. Ишханян «Математический анализ»,
Ч.1, 2.
4. Минорский В.П. «Сборник задач по высшей
математике».
3.
1. ФУНКЦИЯ ДВУХ ПЕРЕМЕННЫХ.1.1. Определение, способы задания
А) Табличное задание функции
y1
y2
...
ym
x1
z11
z12
…
z1m
x2
z21
z22
…
z2m
...
…
…
…
…
xn
zn1
zn2
…
znm
4.
Б) Графическое задание функции (номограммы)z
y=y1
y=y2
y=y3
y=ym
0
a
b
x
5.
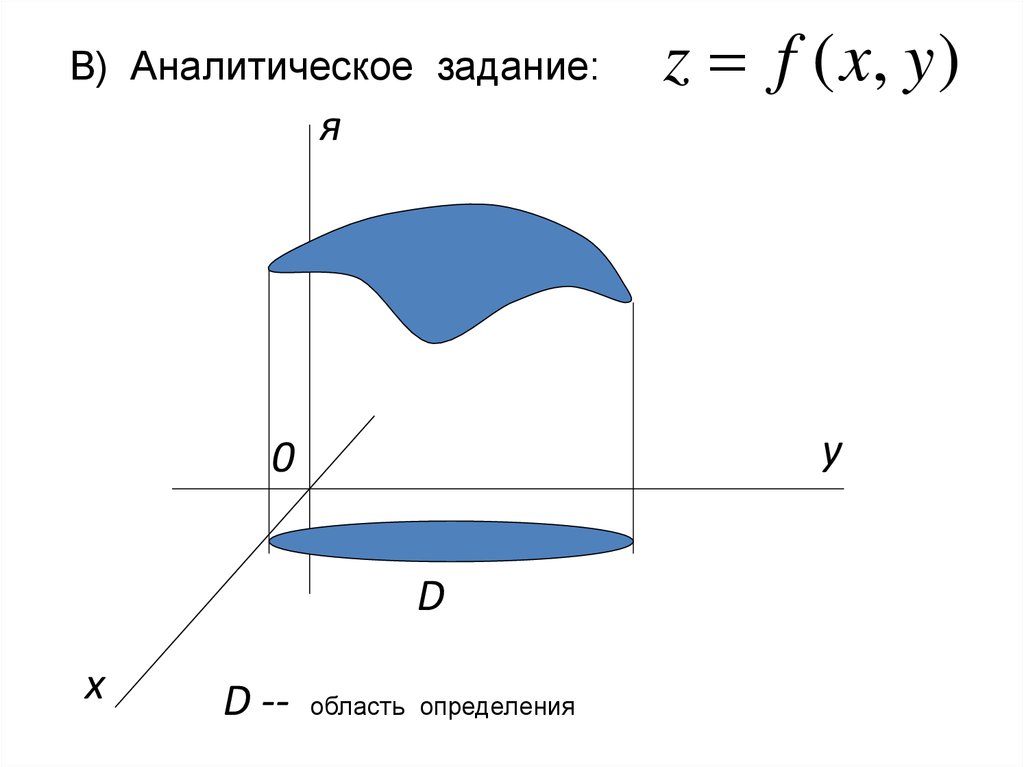
В) Аналитическое задание:z f ( x, y )
я
y
0
D
x
D --
область определения







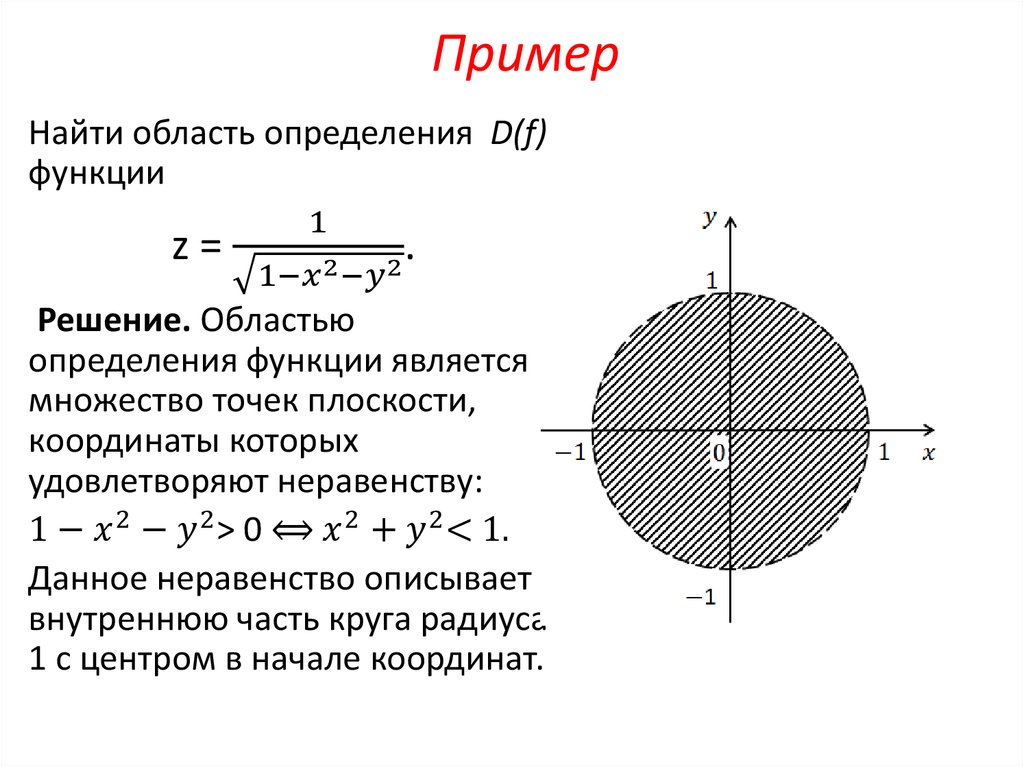

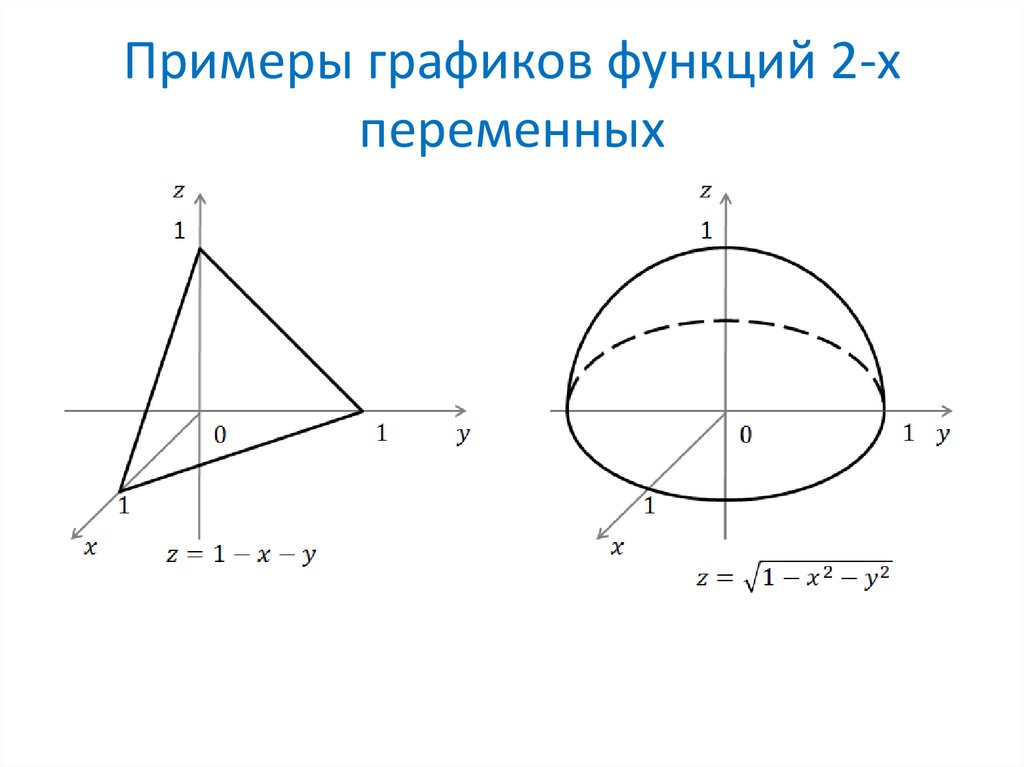

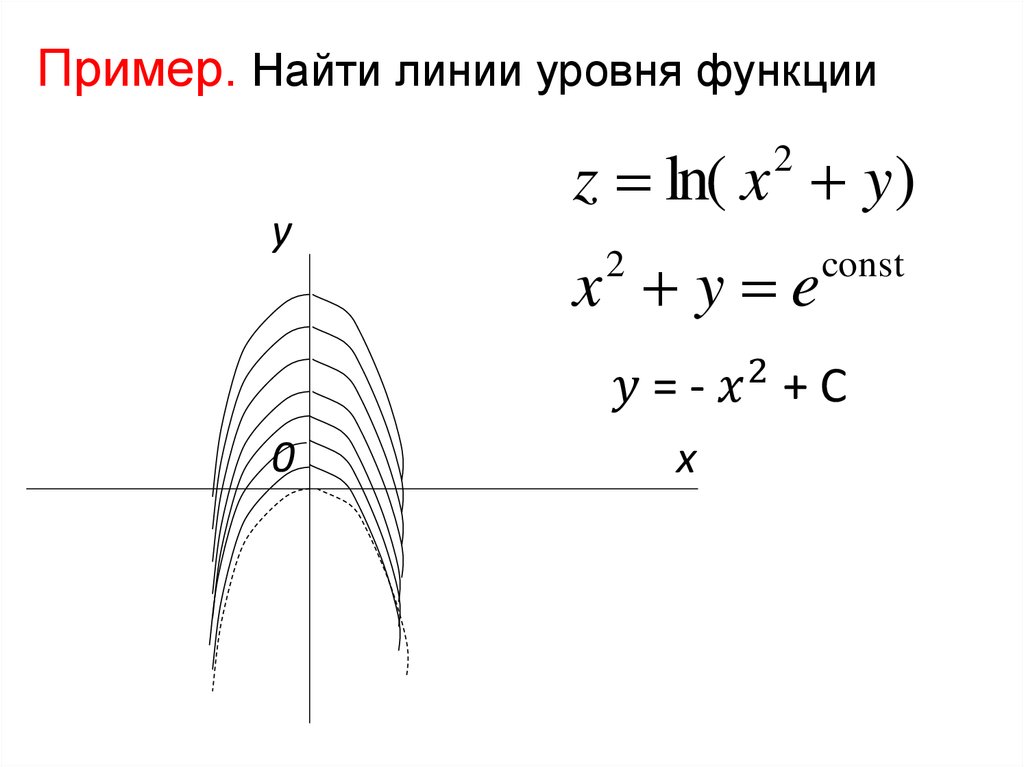














































 Математика
Математика








