Похожие презентации:
Функции нескольких переменных. (Тема 5)
1. Функции нескольких переменных
(ФНП)2. Евклидово пространство Rn
Евклидово пространство Rn
Пусть имеем n действительных чисел х1,х2, х3,...хn,
где ( i ) xi R
Упорядоченный набор (х1,х2, х3,...хn) определяет
n
точку n-мерного пространства R : М R n
Множество точек D {x x ( x1 , , xn )} R n
называется областью (подмножеством)
n
пространства R
Расстоянием между точками х и у называют
величину ( x, y ) x y ( x1 y1 )2 ( xn yn )2
что соответствует обычной евклидовой норме.
3. Определение ФНП
Если каждой точке М(х1,х2, х3,...хn) из множестваn
по некоторому правилу ставится в
D R
соответствие вполне определенное значение
переменной величины z, то говорят, что на
множестве D задана функция нескольких
переменных z = f (х1,х2, х3,...хn)
Обозначения:
х1,х2, х3,...хn – независимые переменные,
аргументы
z – зависимая переменная, функция
f – закон соответствия, правило
n
D – область определения функции,D R
Z – область значений функции,Z R
4. Примеры ФНП
Площадь поверхности прямоугольногопараллелепипеда:
S 2 х1 х2 2 х2 х3 2 х1 х3
где х1, х2, х3
- измерения параллелепипеда
Производственная функция Кобба-Дугласа:
Q А К L1
Зависимая
переменная Q – объем выпуска
продукции,
Аргументы: К – затраты капитала, L- затраты
трудовых ресурсов;
Параметры: А – параметр производительности,
α – доля капитала в доходе
5. Договоренности
Обычно рассматривают функцииz f ( x, y )
двух переменных или
u f ( x, y , z )
трех переменных
Далее рассмотрим функцию двух
переменных (n=2): z f ( x, y )
Все утверждения справедливы при n>2
6. Способы задания ФНП
При аналитическом способе задания используютчаще всего:
явное задание функции, т.е. уравнением вида
z f ( x, y )
неявный способ посредством уравнения,
связывающего три переменные величины:
В этом случае каждую из величин x, y, z можно
рассматривать как неявную функцию двух
остальных.
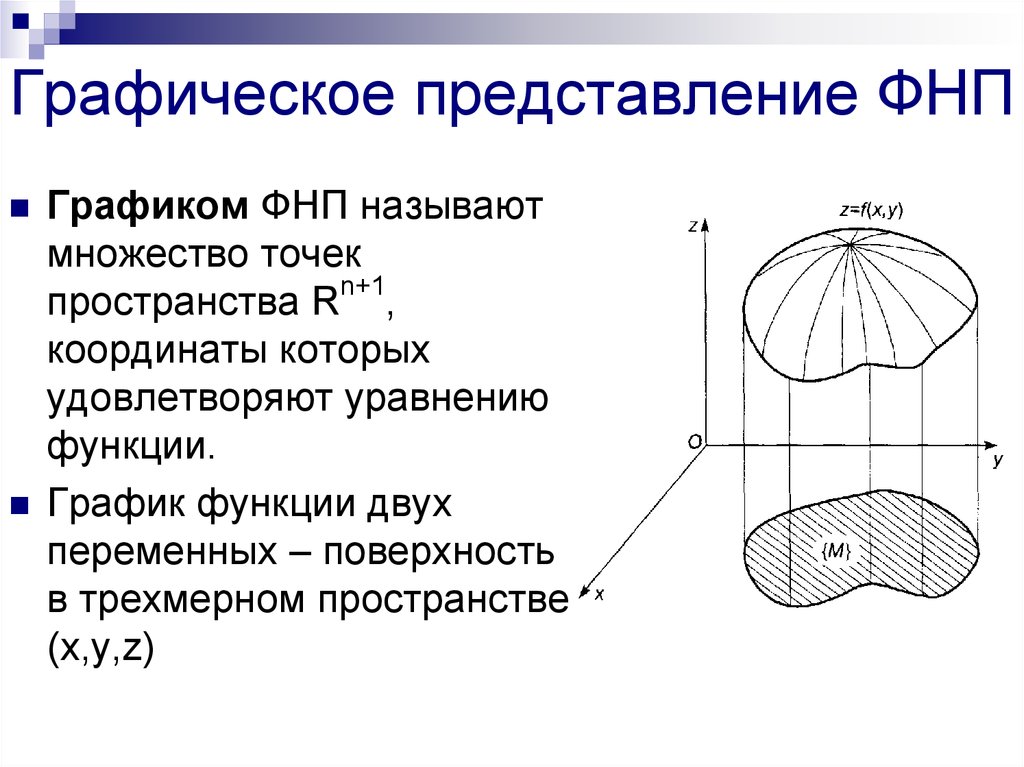
7. Графическое представление ФНП
Графиком ФНП называютмножество точек
n+1
пространства R ,
координаты которых
удовлетворяют уравнению
функции.
График функции двух
переменных – поверхность
в трехмерном пространстве
(x,y,z)
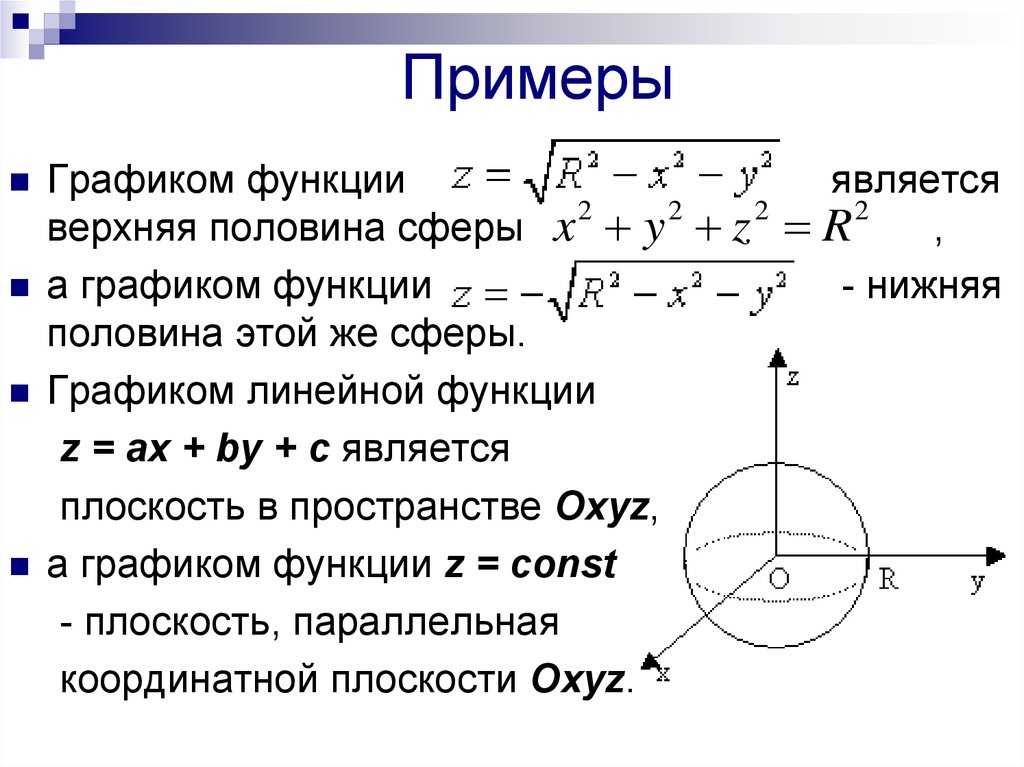
8. Примеры
Графиком функцииявляется
2
2
2
2
верхняя половина сферы x y z R
,
а графиком функции
- нижняя
половина этой же сферы.
Графиком линейной функции
z = ax + by + с является
плоскость в пространстве Oxyz,
а графиком функции z = сonst
- плоскость, параллельная
координатной плоскости Oxyz.
9. Примеры
Построить график функции z ( xПостроим график в системе Maple
2
y 1)
2
10. Графическое представление ФНП
Линией (поверхностью)уровня функции
нескольких переменных
называется множество
таких точек на плоскости,
что значение функции в
них одно и то же и равно С.
Число С называют
уровнем.
11. График и линии уровня ФНП
12. Предел и непрерывность функций нескольких переменных
13. Окрестности точки в Rn
Круговой δ-окрестностью Uδ точки М0 (x0, y0)называется круг радиуса δ с центром в точке M0,
т.е. множество точек M (x, y), координаты которых
удовлетворяют неравенству
Прямоугольной δ-окрестностью Vδ точки М0
(x0, y0) называется прямоугольник
с центром в точке M0 со сторонами 2δ.
14. Предел ФНП в точке
Число A называется пределом функции f (x, y) прии
, если для любого числа ε>0 можно найти такое
число δ>0, что неравенство
выполняется
для всех точек М(х,у) из δ-окрестности точки М0 (x0, y0).
Обозначения:
Символически:
А lim f ( x, y) ( 0)( 0) M U (M 0 ) f ( x, y) A
x x0
y y0
Геометрический смысл определения: в точках
достаточно малой окрестности точки М0 значения функции
f(х, у) как угодно мало отличаются от числа А.
15. Предел ФНП
Понятия предела функций одной и нескольких переменныхво многом аналогичны:
Рассматривают предел в бесконечно удаленной точке,
Используют понятия бесконечно большой и бесконечно
малой функций;
Имеют место те же теоремы о свойствах пределов;
Используют те же приемы вычисления пределов.
НО основное различие между ними касается условия
существования предела: для ФНП стремление к
предельной точке может происходить по бесконечному
числу направлений, потому для существования предела у
ФНП должны совпадать пределы по всем возможным
направлениям.
16. Пример
Найти предел limx 0
y 0
ln( 1 x 2 y 2 )
x2 y2
Решение
Обозначим x 2 y 2 . Условие х→0, у→0
равносильно ρ→0.
Перейдем в пределе к переменной ρ:
ln( 1 x 2 y 2 )
ln( 1 2 ) 0
(ln( 1 2 ))
lim
lim
lim
2
2
x 0
0
0
0
x y
y 0
1
( 2 )
2
0
1
lim
0
0
1
1
17. Пример
НайтиРешение
По любой прямой предел один и тот же:
С другой стороны, пусть стремление к предельной
точке происходит по кривой
Тогда
Следовательно, предел не существует.
18. Непрерывность ФНП
Пусть функция z f ( x, y ) определена вокрестности Uδ точки М0 (x0, y0).
Функция называется непрерывной в точке
М0 (x0, y0), если
Функция непрерывна в точке тогда и только тогда,
когда бесконечно малым приращениям аргументов
соответствует бесконечно малое приращение
функции:
Функцию, непрерывную в каждой точке области D,
называют непрерывной в этой области.
19. Пример
Исследовать на непрерывность функциюРешение
Функция определена при всех значениях
переменных x и y, кроме начала координат, где
знаменатель обращается в нуль.
Многочлен x2+y2 непрерывен всюду → непрерывен
корень квадратный из непрерывной функции →
дробь непрерывна всюду, кроме точек, где её
знаменатель равен нулю.
Итак, рассматриваемая функция непрерывна на
всей координатной плоскости Оху, исключая
начало координат.
20. Дифференциальное исчисление функций нескольких переменных
21. Частные производные ФНП первого порядка
Пусть функция z f ( x, y ) двух переменных определенав области D, а М0 (x0, y0) – внутренняя точка области D.
Дадим аргументу x приращение Δx = x - x0, тогда функция z
получит частное приращение по x:
x z x f f ( x0 x, y0 ) f ( x0 , y0 )
Если существует конечный предел
xz
f ( x0 x, y0 ) f ( x0 , y0 )
lim
lim
x 0 x
x 0
x
то этот предел называется частной производной
функции z f ( x, y ) по х в точке М0 и обозначается
одним из символов:
f
f
z
,
z x ( M 0 ), f x (M 0 ), f x ( x0 , y0 ),
,
x M 0
x ( x0 , y0 )
x M 0
22. Частные производные ФНП первого порядка
Аналогично определяется частная производная по у.Используются обозначения: z у , f y , z , f
у
y
Производные f х , f y называются частными
производными первого порядка или первыми
частными производными.
Частная производная по какой-либо переменной есть
обычная производная, при условии, что все остальные
переменные – константы.
Правила и формулы дифференцирования функций одной
переменной справедливы при нахождении частных
производных ФНП.
23. Пример
Найти частные производные функцииРешение
u z
xy
24. Геометрический смысл частных производных ФНП
Пусть поверхность Р –график функции z f ( x, y )
При у=у0 получим:
кривая Гх – сечение Р;
α – угол наклона касательной к
кривой Гх в точке (х0,у0) к оси Ох;
z x ( x0 , y0 ) tg
Аналогично при х=х0
z y ( x0 , y0 ) tg
25. Пример
Какой угол образует с осью Ох касательная к линиив точке М (2,4,5)?
Решение
Так как значение у фиксировано (у=4), используем
геометрический смысл частной производной по
переменной х (при постоянном у):
значение в точке М
Следовательно
и α=450
26. Полный дифференциал
Пусть функция z f ( x, y ) определена в области D, аМ0 (x0, y0) – внутренняя точка области D.
Дадим ее аргументам x и у соответствующие приращения
Δx и Δу, тогда функция z получит полное приращение:
z f ( x0 x, y0 y) f ( x0 , y0 )
Существенную часть полного приращения функции
составляет ее дифференциал
Дифференциалом (полным дифференциалом) ФНП
называется сумма произведений частных производных
этой функции на приращения соответствующих
независимых переменных:
dz z x x z y y z x dx z y dy
27. Дифференцируемость ФНП
Функция z f ( x, y ) называется дифференцируемой вточке (х0, у0), если ее полное приращение может быть
z dz x y
представлено в виде
где α и β- бесконечно малые относительно Δx и Δу.
Для дифференцируемости ФНП существование у нее
частных производных является лишь необходимым, но
недостаточным условием.
Достаточное условие дифференцируемости ФНП: если
частные производные z х , z y существуют в окрестности
точки (х0, у0) и непрерывны в самой точке, то функция
z f ( x, y )дифференцируема в этой точке
28. Производная по направлению
Пусть функция z f ( x, y ) определена в окрестности точкиМ0 (x0, y0); l - некоторое направление
При перемещении точки М0 (x0, y0) в данном направлении l
в точку М (x, y) функция z получит приращение
l z f ( x0 x, y0 y) f ( x0 , y0 )
- приращение функции z в данном направлении l.
Производной функции z по направлению l называется
предел
l z
f ( x0 x, y0 y ) f ( x0 , y0 )
zl lim
lim
l 0 x
l 0
l
Производная по направлению характеризует скорость
изменения функции в данном направлении
29. Градиент
Градиентом функции z f ( x, y ) называется вектор,координаты которого равны соответственно частным
производным:
gradz z ( z x , z y )
Связь градиента функции с производной
по направлению l
определяется равенством zl z e z x cos z y cos
где e (cos , cos ) – единичный вектор, задающий
направление l.
Градиент функции характеризует направление и величину
максимальной скорости возрастания функции в точке.
Зная градиент функции в каждой точке, можно локально
строить линии уровня, т.к. градиент перпендикулярен линии
уровня.
30. Частные производные ФНП высших порядков
Частные производные первого порядка сами являютсяфункциями нескольких переменных, их также можно
дифференцировать.
Для функции z f ( x, y ) возможны четыре вида частных
производных второго порядка:
z xx ( z x ) x , z xy ( z x ) y , z yx ( z y ) x , z yy ( z y ) y ,
и восемь – третьего порядка:
В случае большего числа аргументов все вторые частные
производные функции u = u(x1,…,xn) можно записать с
помощью матрицы Гессе:
u x x
u x x u x x
u
x x
матрицы Гессе : 2 1
u xn x1
1 1
1 2
u x2 x2
u xn x2
u x2 xn
u xn xn
1 n
31. Частные производные ФНП высших порядков
Частные производные, в которых дифференцированиепроизводится по одинаковым переменным называются
повторными; по разным переменным - смешанными.
Если функция нескольких переменных необходимое
количество раз дифференцируема в точке (имеет
непрерывные частные производные), то ее смешанные
производные в этой точке равны.
В силу равенства смешанных производных матрица Гессе
симметрична
32. Экстремумы функции нескольких переменных
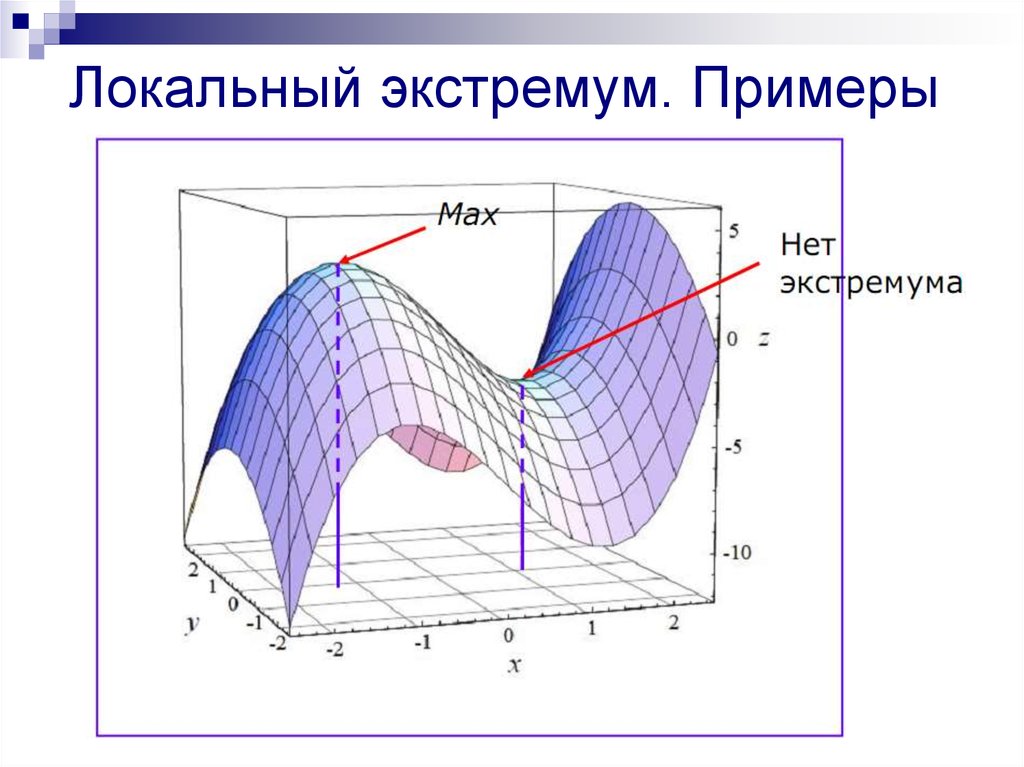
33. Локальный экстремум ФНП
Точка М0 (x0, y0) называется точкой максимума(локального максимума) функции z f ( x, y ) , если
существует окрестность UM0 точки М0, в каждой точке М
которой выполняется неравенство f(M0)≥f(M)
Точка М0 (x0, y0) называется точкой минимума
(локального минимума) функции
, если
существует окрестность UM0 точки М0, в каждой точке М
которой выполняется неравенство f(M0) ≤f(M)
z f ( x, y )
34. Локальный экстремум ФНП
В критических точках функция можетиметь экстремум, а может не иметь,
т.е. необходимое условие
экстремума не является
достаточным
35. Локальный экстремум ФНП
Достаточное условие экстремума ФНП:Пусть функция z f ( x, y ) имеет непрерывные частные
производные второго порядка в некоторой окрестности
критической точки М0:
Тогда
если
то экстремум есть,
причем при А > 0 в точке М0 – минимум функции;
при А < 0 - максимум.
если
то экстремума в точке М0 нет;
если
то требуется дополнительное
исследование
36. Локальный экстремум ФНП
1.2.
3.
4.
5.
Схема исследования ФНП на экстремум
Найти частные производные первого порядка
Найти критические точки, решая систему
уравнений z x 0
z y 0
Найти частные производные второго порядка
Вычислить значения вторых производных в
критических точках, проверить достаточные
условия экстремума
Найти экстремальные значения функции.
37. Локальный экстремум. Примеры
38.
Локальный экстремум. Примеры39. Локальный экстремум. Примеры
Исследовать на экстремум функциюРешение
Найдем
Критические точки:
→
Найдем
Проверка достаточных условий:
проведем дополнительное исследование –
рассмотрим ∆z(0;0)=z(h,k)-z(0,0)
при
при
приращение ∆z(0;0) принимает значения разных знаков,
поэтому в точке (0;0) экстремума нет.
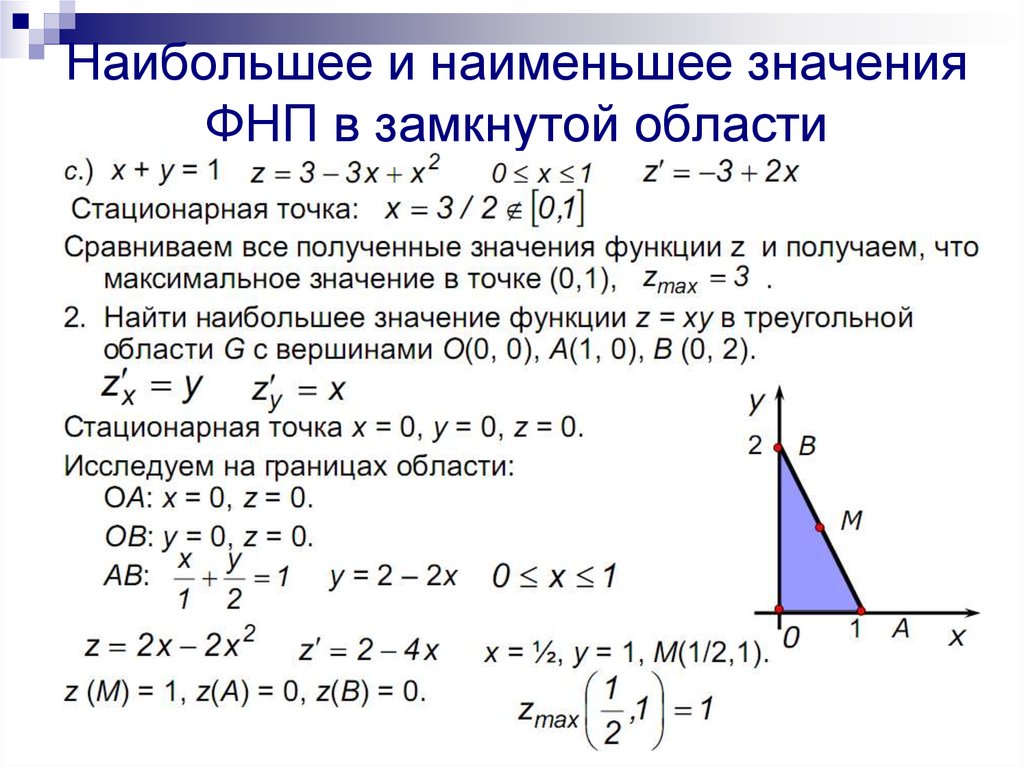
40. Наибольшее и наименьшее значения ФНП в замкнутой области
41. Наибольшее и наименьшее значения ФНП в замкнутой области
42. Наибольшее и наименьшее значения ФНП в замкнутой области
43. Условный экстремум ФНП
Условным экстремумом функции z=f(х,у) называетсяэкстремум этой функции, достигнутый при условии, что
аргументы х и у связаны уравнением g(x,y)=C.
Уравнение g(x,y)=C называется уравнением связи.
Геометрический смысл:
выбор наибольшего (наименьшего)
значения среди точек, лежащих на
линии, определяемой уравнением
связи.
44. Условный экстремум ФНП
1 способ – выражение одной неизвестной из уравнениясвязи
Пример. Найти экстремумы функцииz x 2 2y 2 при
условии 3 x 2 y 11
11 3x
Выразим из уравнения связи переменную у: y
2
Подставив это выражение в функцию z, получим
2
11 3 x 11 2
2
z x 2
( x 6 x 11) z ( x)
2
2
Исследуем ее как функцию одной переменной:
z 5,5 (2 x 6) 0 при x 3 - точка минимума, откуда y 1
Точка (3,1) - точка условного экстремума (минимума):
z min 32 2 12 11
45. Условный экстремум. Метод множителей Лагранжа
2 способ (универсальный) – метод неопределенныхмножителей Лагранжа - используется, когда из
уравнения связи выражение ни одной из переменных
невозможно или число переменных больше двух.
Алгоритм метода:
Составить функцию Лагранжа:
1.
( x, y , ) f ( x, y ) g ( x, y )
2.
Исследовать функцию Лагранжа на экстремум как
функцию трех переменных.










































 Математика
Математика








