Функция и ее свойства

1. Функция. Свойства функции.

Лекция №2 по математике. Для студентов 1 курса весенний
семестр отделение «Сестринское дело».
Составила преподаватель математики Чухарева Ю.И.
2017

2. Определение .

Функция – это «закон»
однозначного соответствие
между элементами двух
множеств Х и Y.
2

3. Определение .

Говорят, что
наjjмножестве Х имеется функция (отоб
ражение, операция, оператор) f со
значениями из Y, если каждому элементу х
из множества Х по правилу f поставлен в
соответствие некоторый элемент y из
множества Y.
3

4. Определение .

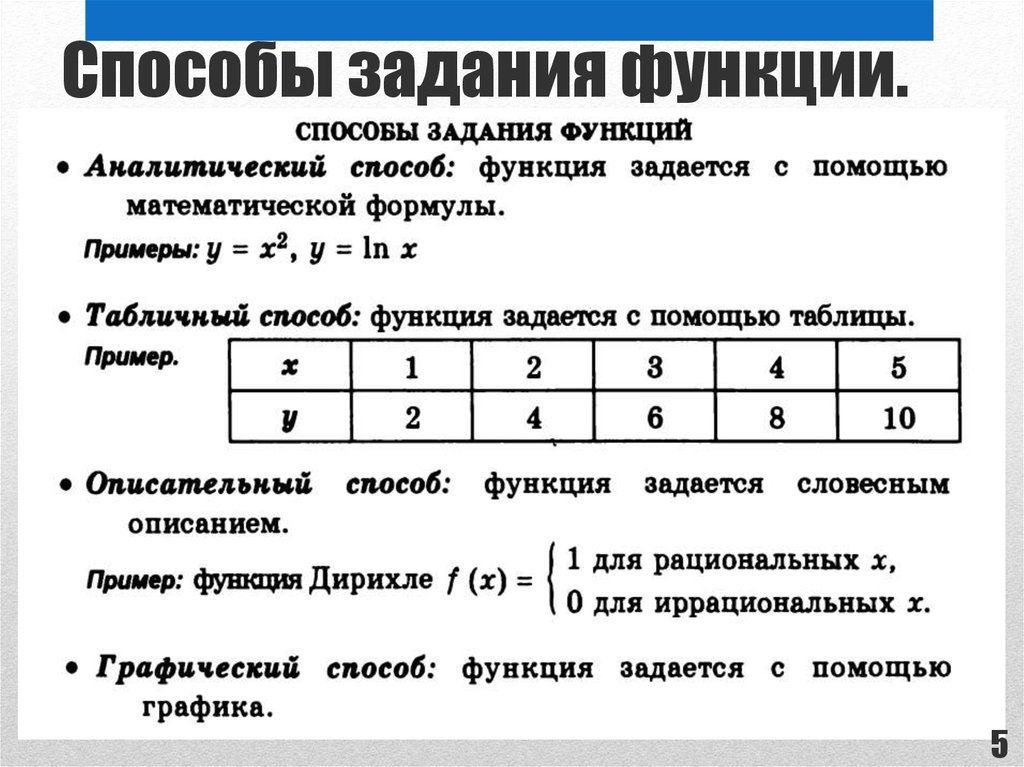
4

5. Способы задания функции.

5

6. Основные свойства функции.

Область определения функции.
Область значения функции.
Четность и нечетность функции.
Периодичность функции.
Точки пересечения графика функции с осями.
Промежутки знакопостоянства.
Асимптоты.
Точки экстремума. (максимум и минимум функции).
Промежутки монотонность функции. (промежутки
возрастание и убывание функции)
• График функции.
• Дополнительные точки.
6

7. Область определения функции.

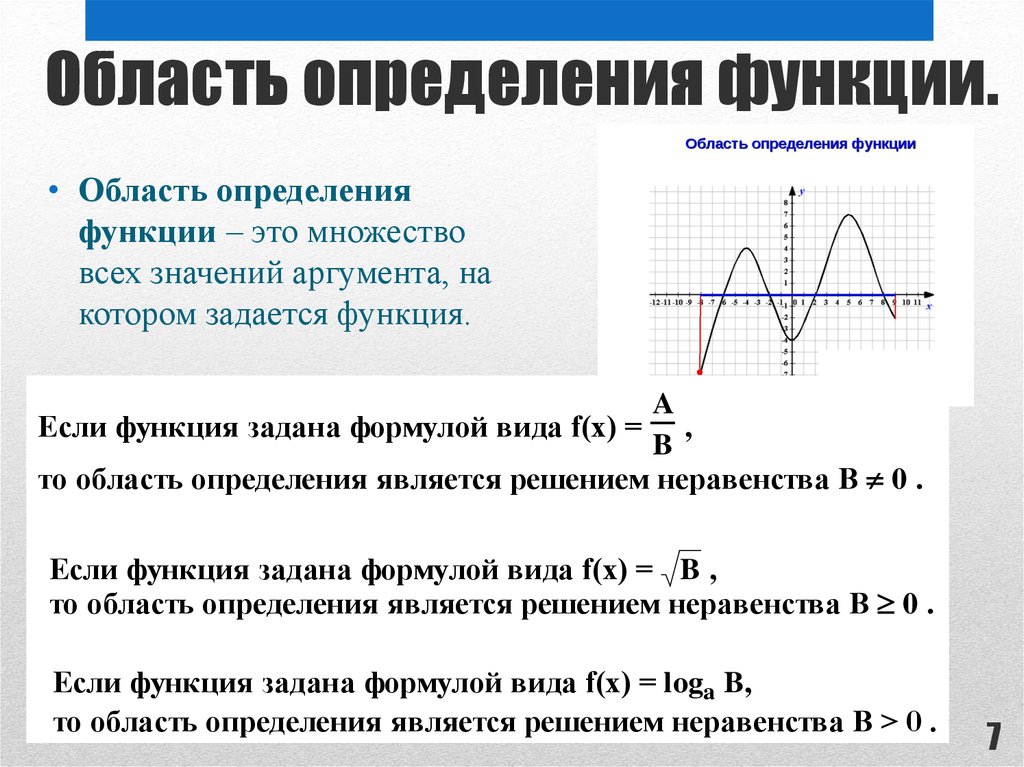
• Область определения
функции – это множество
всех значений аргумента, на
котором задается функция.
A
Если функция задана формулой вида f(x) = ,
B
то область определения является решением неравенства В 0 .
Если функция задана формулой вида f(x) = B ,
то область определения является решением неравенства B 0 .
Если функция задана формулой вида f(x) = loga B,
то область определения является решением неравенства В > 0 .
7

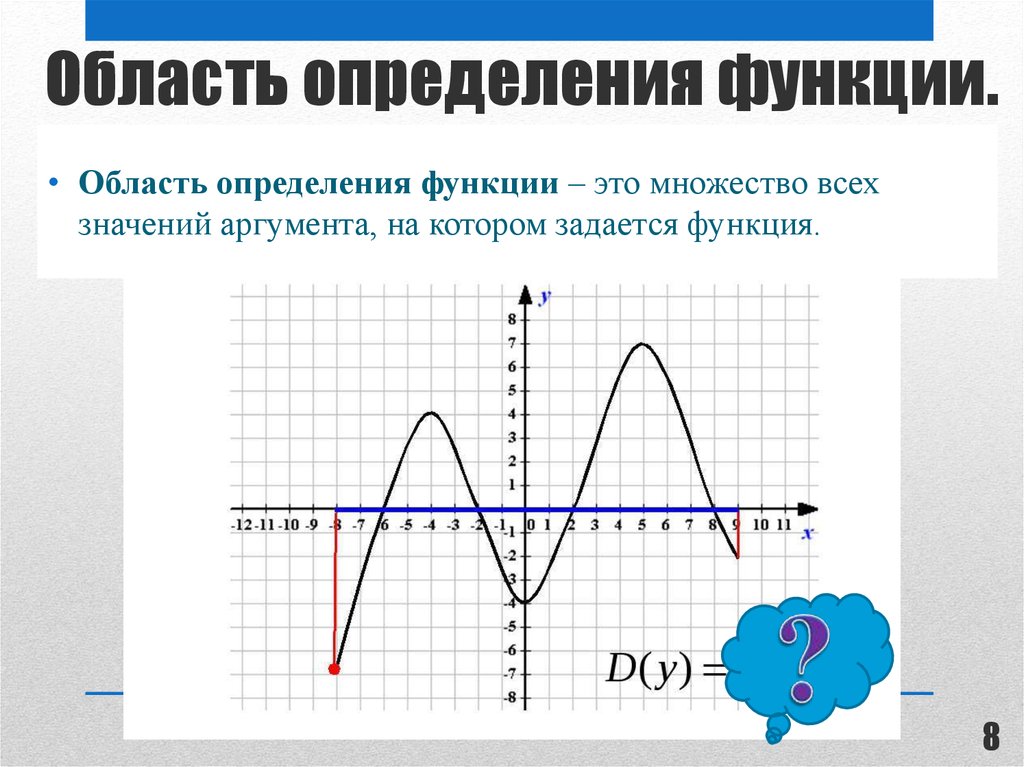
8. Область определения функции.

• Область определения функции – это множество всех
значений аргумента, на котором задается функция.
8

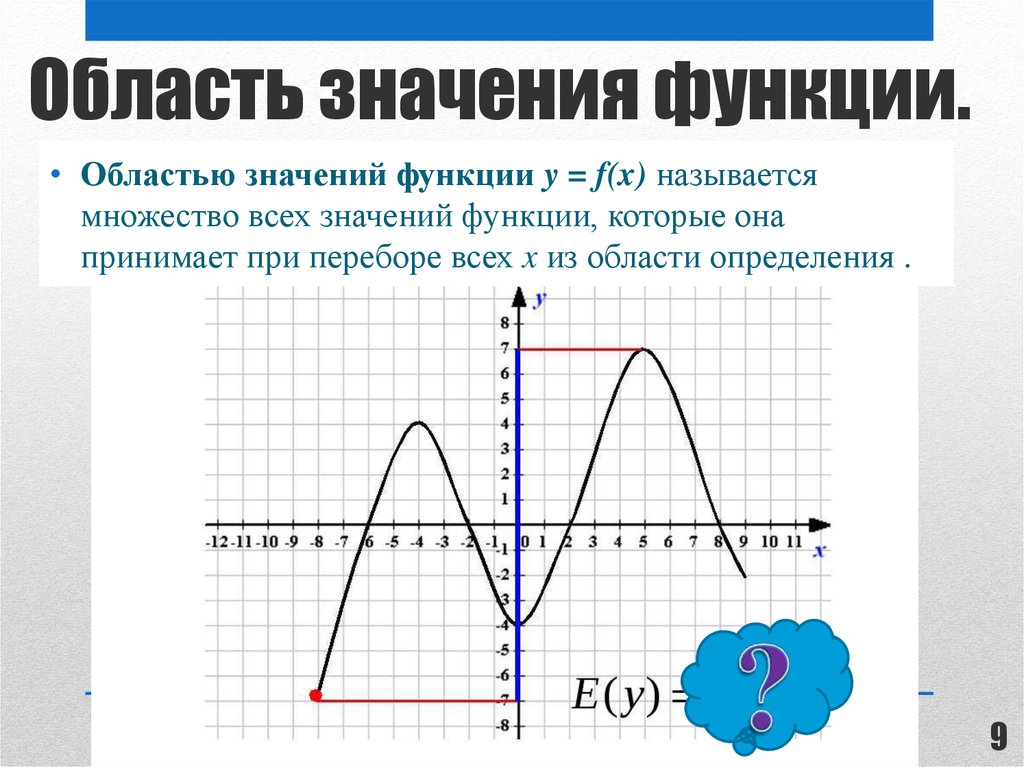
9. Область значения функции.

• Областью значений функции y = f(x) называется
множество всех значений функции, которые она
принимает при переборе всех x из области определения .
9

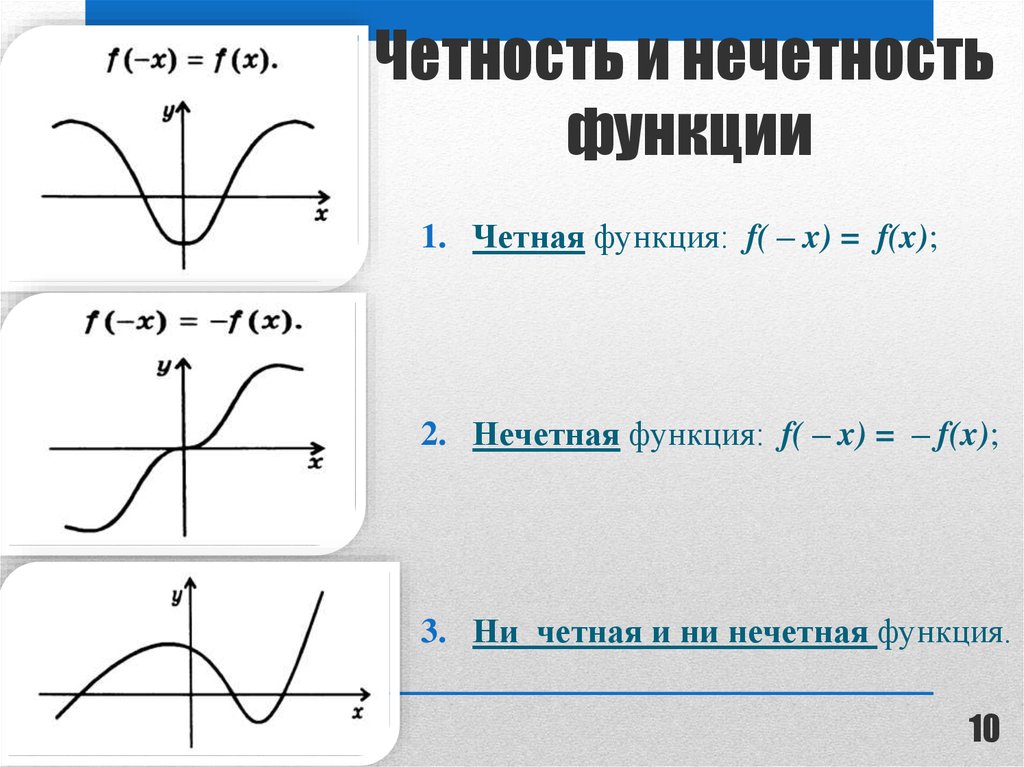
10. Четность и нечетность функции

1. Четная функция: f( – x) = f(x);
2. Нечетная функция: f( – x) = – f(x);
3. Ни четная и ни нечетная функция.
10

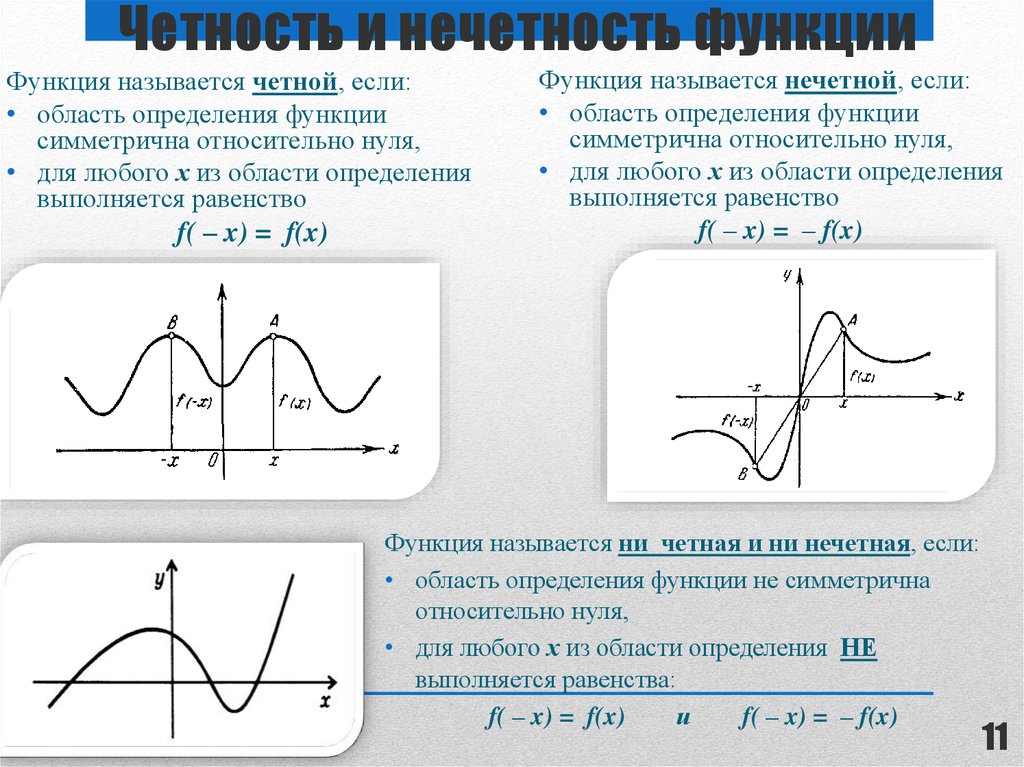
11. Четность и нечетность функции

Функция называется четной, если:
• область определения функции
симметрична относительно нуля,
• для любого х из области определения
выполняется равенство
f( – x) = f(x)
Функция называется нечетной, если:
• область определения функции
симметрична относительно нуля,
• для любого х из области определения
выполняется равенство
f( – x) = – f(x)
Функция называется ни четная и ни нечетная, если:
• область определения функции не симметрична
относительно нуля,
• для любого х из области определения НЕ
выполняется равенства:
f( – x) = f(x)
и
f( – x) = – f(x)
11

12. Периодичность функции.

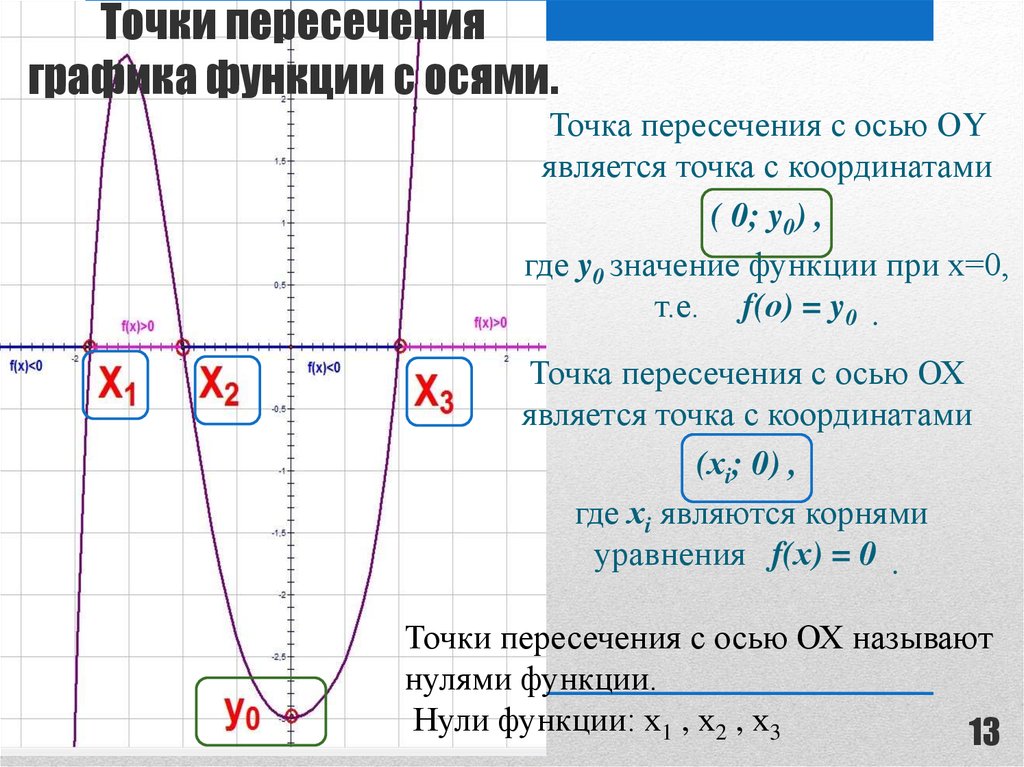
12

13. Точки пересечения графика функции с осями.

Точка пересечения с осью ОY
является точка с координатами
( 0; y0) ,
где y0 значение функции при х=0,
т.е. f(о) = y0 .
Точка пересечения с осью ОХ
является точка с координатами
(хi; 0) ,
где хi являются корнями
уравнения f(х) = 0 .
Точки пересечения с осью ОХ называют
нулями функции.
Нули функции: х1 , х2 , х3
13

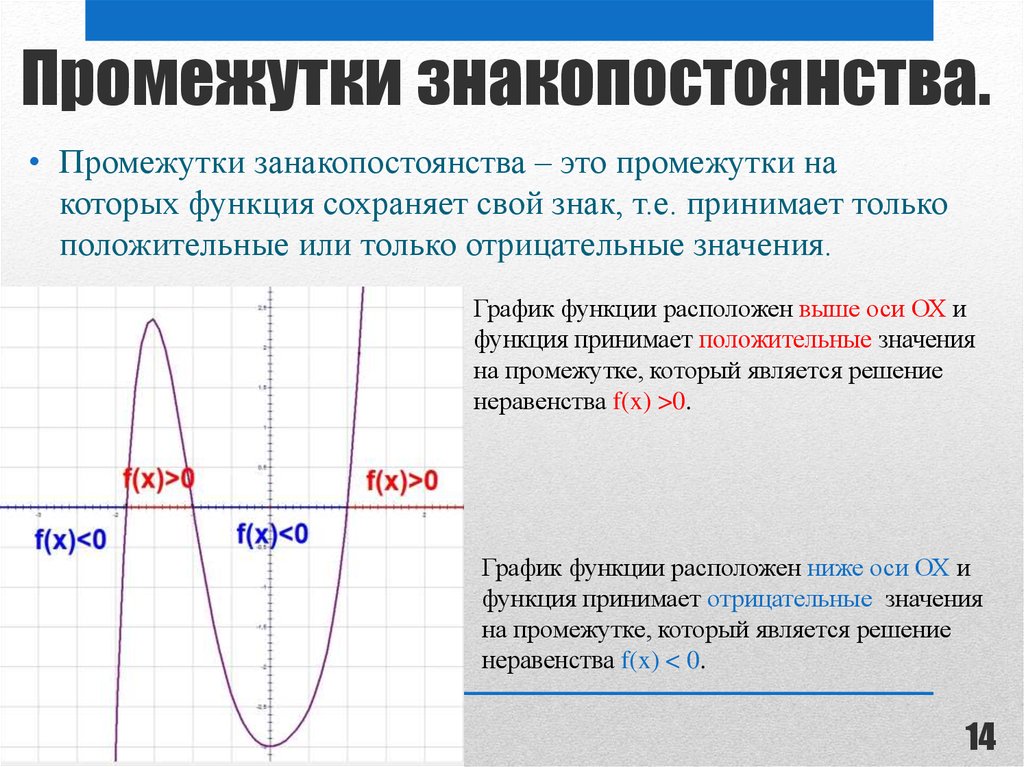
14. Промежутки знакопостоянства.

• Промежутки занакопостоянства – это промежутки на
которых функция сохраняет свой знак, т.е. принимает только
положительные или только отрицательные значения.
График функции расположен выше оси ОХ и
функция принимает положительные значения
на промежутке, который является решение
неравенства f(x) >0.
График функции расположен ниже оси ОХ и
функция принимает отрицательные значения
на промежутке, который является решение
неравенства f(x) < 0.
14

15. Асимптота.

15

16. Асимптота.

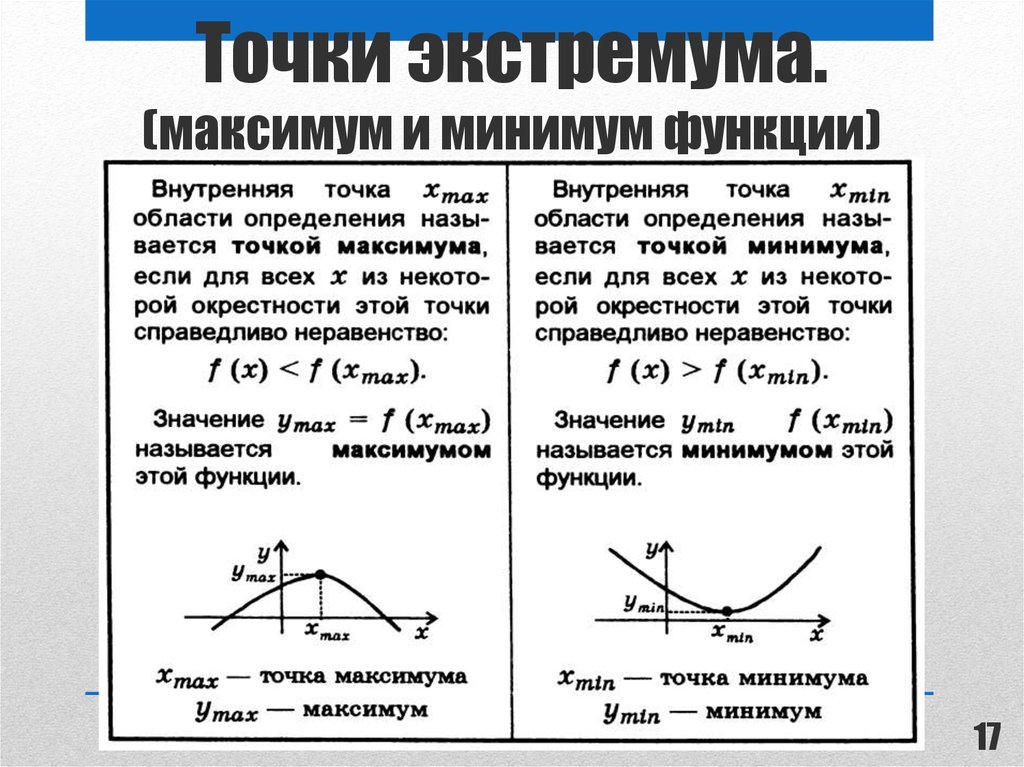
16

17. Точки экстремума. (максимум и минимум функции)

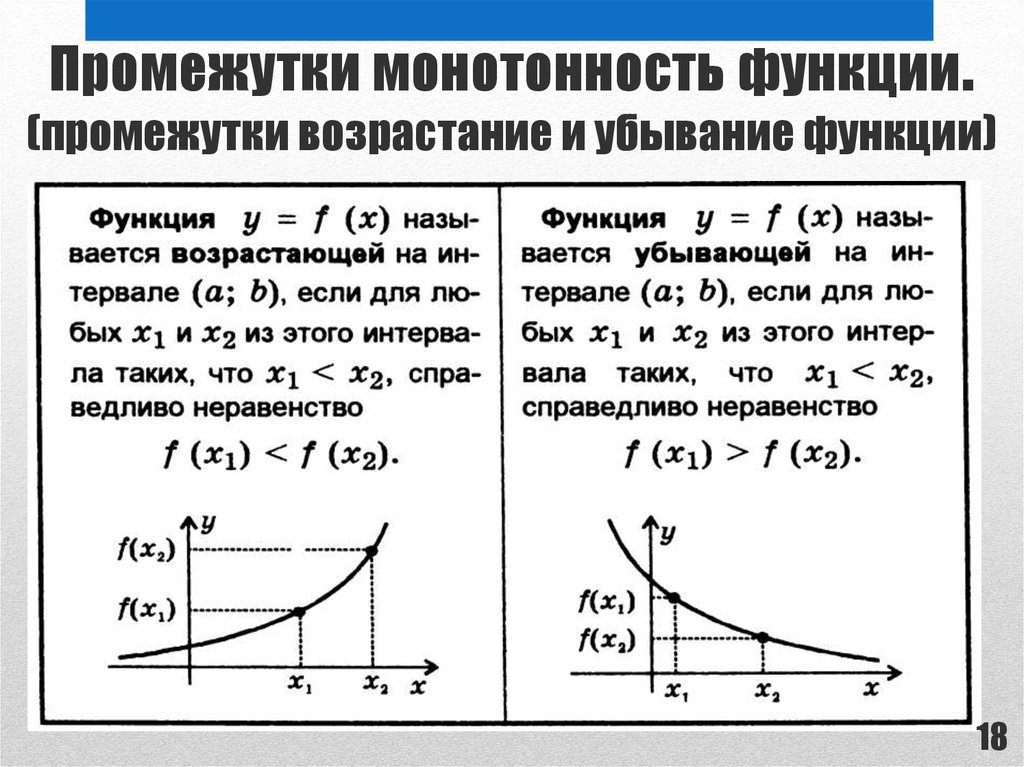
17

18. Промежутки монотонность функции. (промежутки возрастание и убывание функции)

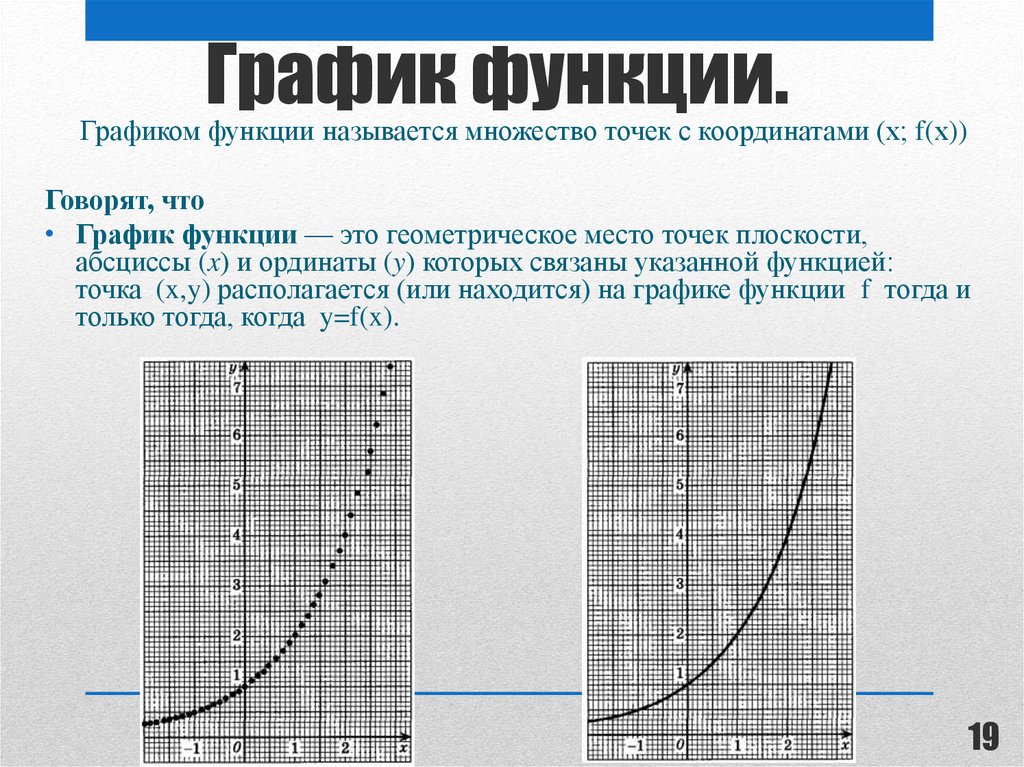
18

19. График функции.

Графиком функции называется множество точек с координатами (х; f(х))
Говорят, что
• График функции — это геометрическое место точек плоскости,
абсциссы (x) и ординаты (y) которых связаны указанной функцией:
точка (x,y) располагается (или находится) на графике функции f тогда и
только тогда, когда y=f(x).
19

20. Дополнительные точки

• По результатам исследования функции строится график
функции. Для точности построения можно задать точки и
найти значение функции в этих точках.
20

21. Литература и Интернет ресурсы

• Учебники по Алгебре для 10 и 11 классов.
• Наглядный справочник по алгебре и началам анализа. 7-11кл
Генденштейн, Ершова 1997 -96с.
• Математический анализ элементарных функций Крейн С.Г.,
Ушакова В.Н_1963 -168с.
• http://www.alleng.ru/index.htm
• http://www.cleverstudents.ru
• http://mathprofi.ru
• http://bigslide.ru/matematika/7286-funkciya-oblast-opredeleniya-ioblast-znacheniy-fu.html
• https://ru.wikipedia.org/wiki
• Для создания некоторых слайдов использовалась программа
«Живая геометрия»
21

22. Желаем успехов.

22