Функция. Свойства функции

1. Функция. Свойства функции.

-
-
область определения;
область значений;
пересечение с осью абсцисс;
монотонность;
экстремумы;
чётность / нечётность;
ограниченность;
периодичность;
наибольшее и наименьшее значения.

2.

у
у
у
у2
у1
хо
у1
хо
О
у2
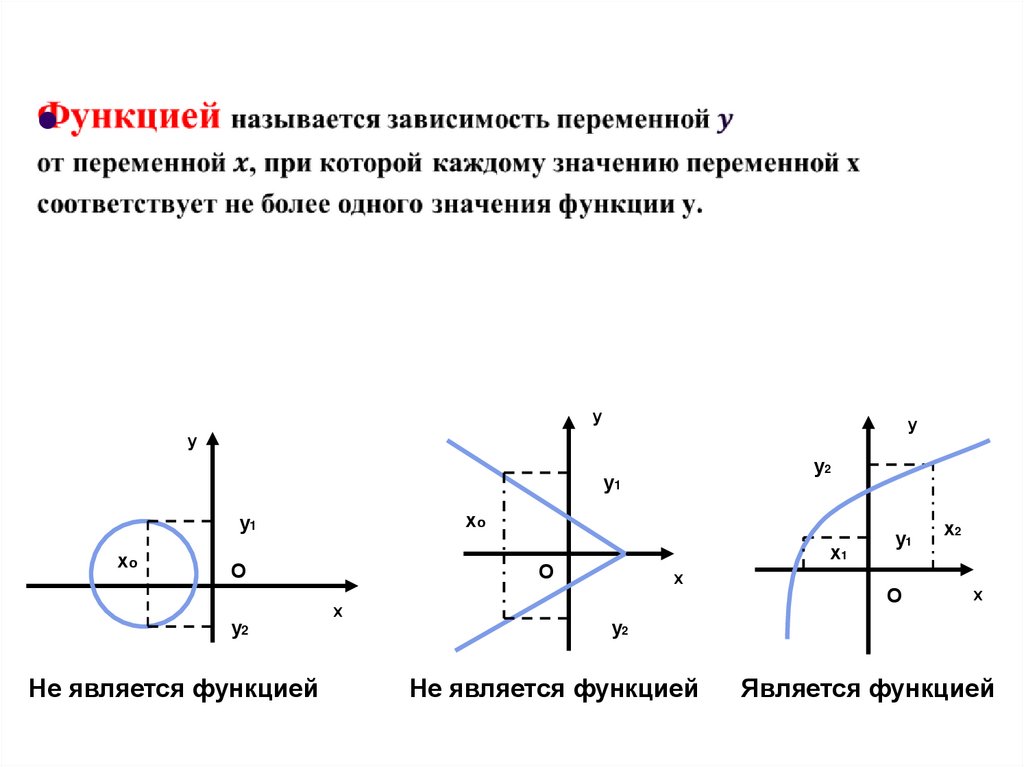
Не является функцией
х1
О
х
х
у1
О
х2
х
у2
Не является функцией
Является функцией

3. Свойства функции

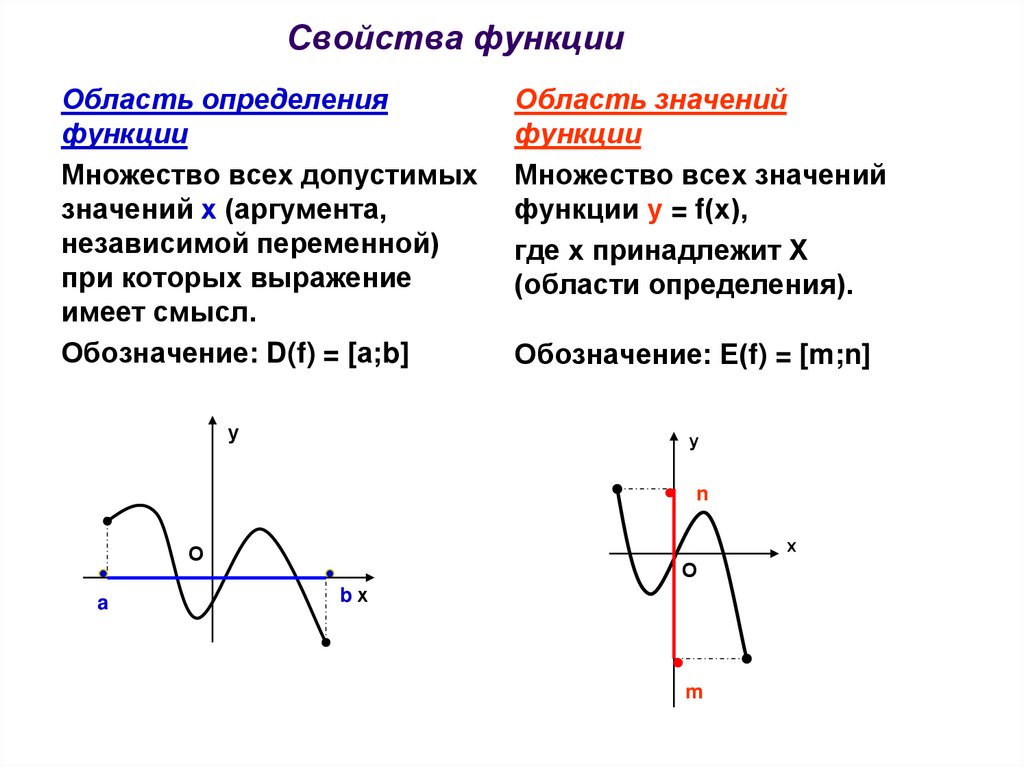
Область определения
функции
Множество всех допустимых
значений х (аргумента,
независимой переменной)
при которых выражение
имеет смысл.
Обозначение: D(f) = [а;b]
у
Область значений
функции
Множество всех значений
функции у = f(х),
где х принадлежит Х
(области определения).
Обозначение: Е(f) = [m;n]
у
n
х
О
a
О
bх
m

4. Пересечение с осью абсцисс

Свойства функции
Пересечение с осью абсцисс
Точки, в которых функция пересекается с осью х
имеют вторую координату y=0.

5. Свойства функции

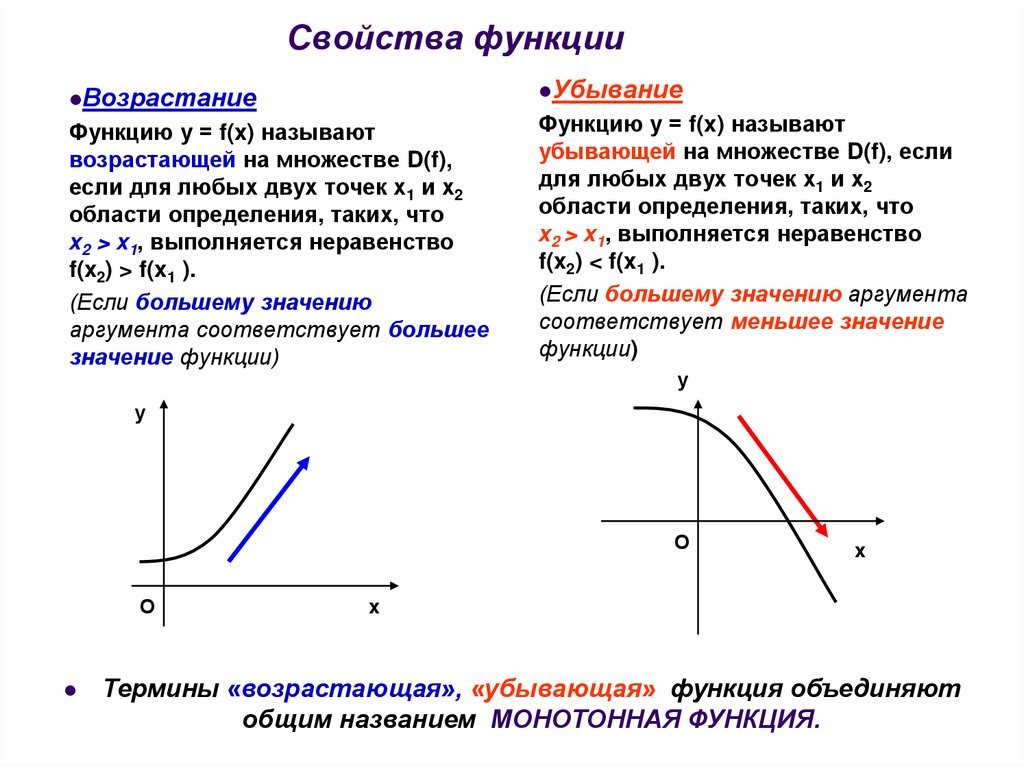
Убывание
Возрастание
Функцию у = f(x) называют
возрастающей на множестве D(f),
если для любых двух точек х1 и х2
области определения, таких, что
х2 > х1, выполняется неравенство
f(x2) > f(x1 ).
(Если большему значению
аргумента соответствует большее
значение функции)
Функцию у = f(x) называют
убывающей на множестве D(f), если
для любых двух точек х1 и х2
области определения, таких, что
х2 > х1, выполняется неравенство
f(x2) < f(x1 ).
(Если большему значению аргумента
соответствует меньшее значение
функции)
у
у
О
О
x
x
Термины «возрастающая», «убывающая» функция объединяют
общим названием МОНОТОННАЯ ФУНКЦИЯ.

6. Экстремумы

Свойства функции
Экстремумы
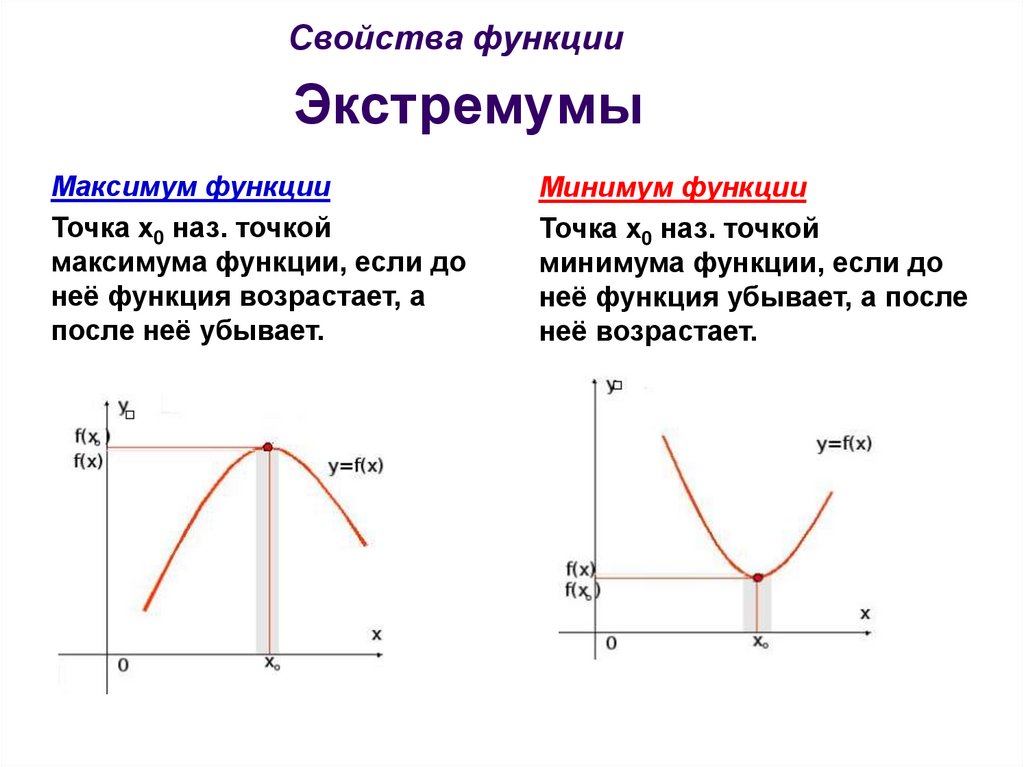
Максимум функции
Точка х0 наз. точкой
максимума функции, если до
неё функция возрастает, а
после неё убывает.
Минимум функции
Точка х0 наз. точкой
минимума функции, если до
неё функция убывает, а после
неё возрастает.

7. Четность, нечетность функции

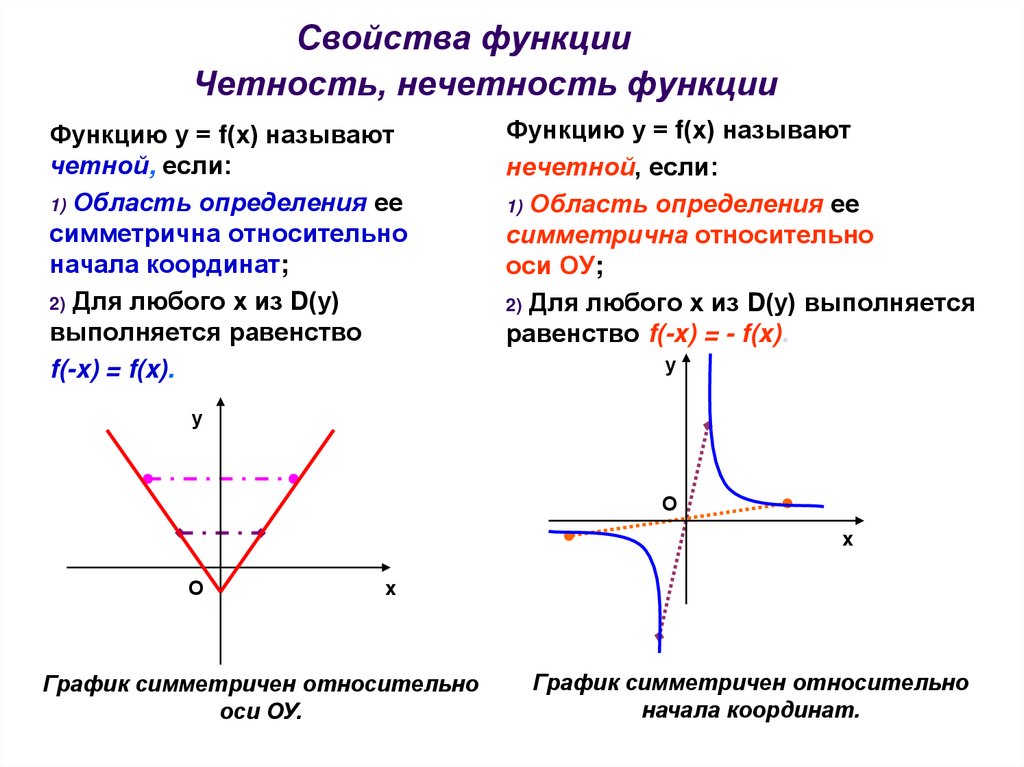
Свойства функции
Четность, нечетность функции
Функцию у = f(х) называют
четной, если:
1) Область определения ее
симметрична относительно
начала координат;
2) Для любого х из D(у)
выполняется равенство
f(-x) = f(x).
Функцию у = f(х) называют
нечетной, если:
1) Область определения ее
симметрична относительно
оси ОУ;
2) Для любого х из D(у) выполняется
равенство f(-x) = - f(x).
у
у
О
x
О
x
График симметричен относительно
оси ОУ.
График симметричен относительно
начала координат.

8. Ограниченность функции

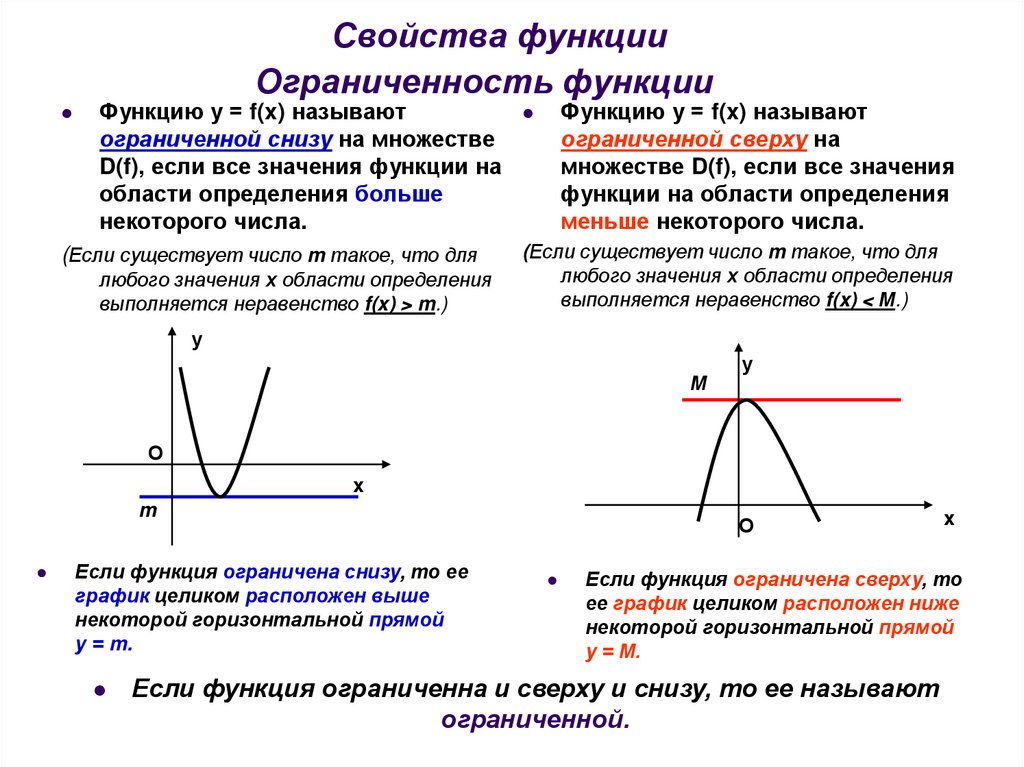
Свойства функции
Ограниченность функции
Функцию у = f(x) называют
ограниченной снизу на множестве
D(f), если все значения функции на
области определения больше
некоторого числа.
(Если существует число m такое, что для
любого значения х области определения
выполняется неравенство f(x) > m.)
Функцию у = f(x) называют
ограниченной сверху на
множестве D(f), если все значения
функции на области определения
меньше некоторого числа.
(Если существует число m такое, что для
любого значения х области определения
выполняется неравенство f(x) < М.)
у
М
у
О
x
m
Если функция ограничена снизу, то ее
график целиком расположен выше
некоторой горизонтальной прямой
у = m.
О
x
Если функция ограничена сверху, то
ее график целиком расположен ниже
некоторой горизонтальной прямой
у = М.
Если функция ограниченна и сверху и снизу, то ее называют
ограниченной.

9.

Свойства функции
Периодичность функции

10. Наибольшее (наименьшее) значения функции

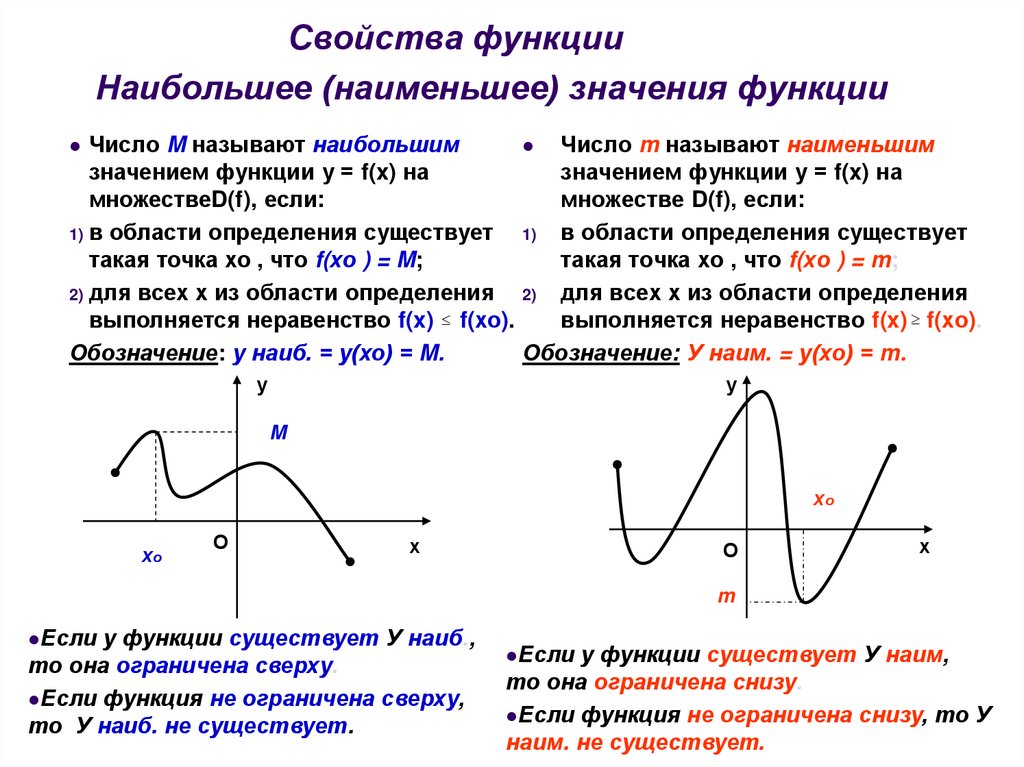
Свойства функции
Наибольшее (наименьшее) значения функции
Число M называют наибольшим
Число m называют наименьшим
значением функции у = f(x) на
значением функции у = f(x) на
множествеD(f), если:
множестве D(f), если:
1) в области определения существует
1)
в области определения существует
такая точка хо , что f(хо ) = M;
такая точка хо , что f(хо ) = m;
2) для всех х из области определения
2)
для всех х из области определения
выполняется неравенство f(x) f(хо).
выполняется неравенство f(x) f(хо).
Обозначение: у наиб. = у(хо) = M.
Обозначение: У наим. = у(хо) = m.
у
у
M
хо
хо
О
х
О
х
m
Если
у функции существует У наиб.,
то она ограничена сверху.
Если функция не ограничена сверху,
то У наиб. не существует.
Если
у функции существует У наим,
то она ограничена снизу.
Если функция не ограничена снизу, то У
наим. не существует.

11. Алгоритм исследования функции

Свойства функции
Алгоритм исследования функции
1.
2.
3.
4.
5.
6.
7.
8.
9.
Область определения.
Область значений.
Пересечение с осью абсцисс
Монотонность (возрастание, убывание).
Экстремумы функции
Четность, нечетность функции.
Ограниченность функции.
Периодичность
Наибольшее, наименьшее значения
функции.

12. Линейная функция

y kx m(k 0)
K>0
у
m
О
х
у
K<0
m
О
х

13. Функция

k
y
x
у
K>0
О
x
у
K<0
О
х

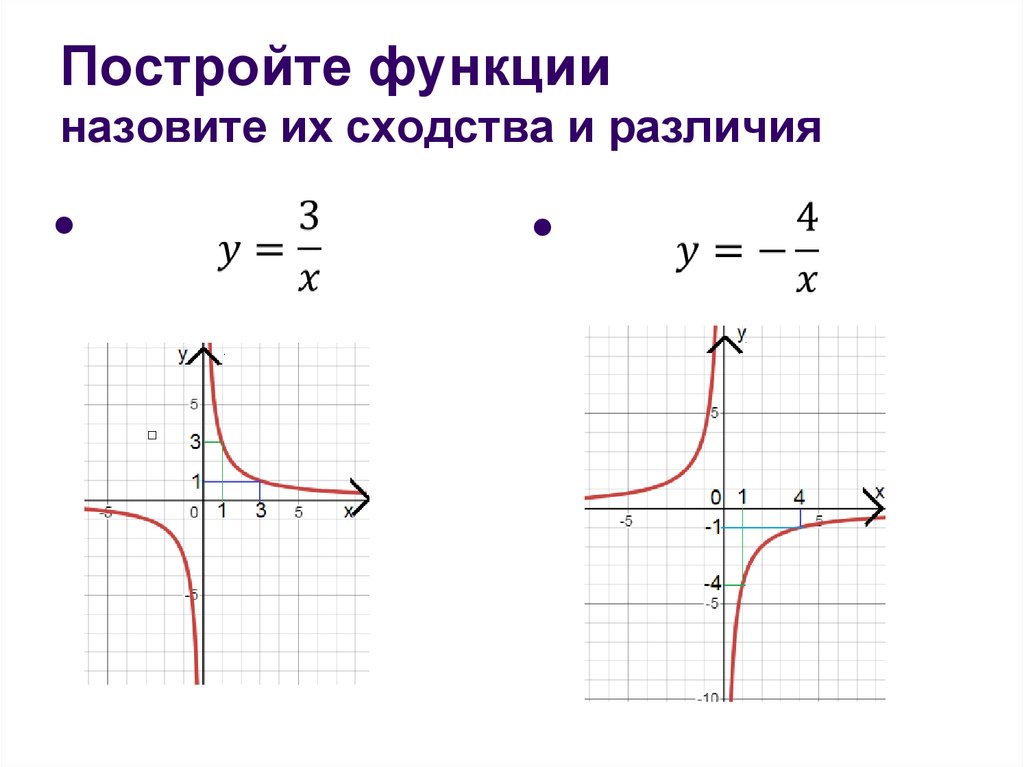
14. Постройте функции назовите их сходства и различия

15. Опишите свойства функции

16.

Самостоятельно выполните
задания Ф 3, которые
находятся в группе «102 СВ
математика» в VK:
https://vk.com/club202575453