Первый закон термодинамики

1. Первый закон термодинамики

Q= U+L
(1)
В технической термодинамике первый закон
формулируется следующим образом:
теплота, подводимая к системе, в общем случае расходуется
как на изменение ее внутренней энергии, так и на
совершение работы изменения объема.
При переходе к удельным величинам выражение
приобретает вид:
q= u + l
(2)
Записывая (2) для бесконечно малого процесса будем иметь:
dq=du+dl
(3)
dq=du+pdv (4)

2. Термодинамические процессы идеального газа

3.

• К основным процессам относятся:
– Изохорный (при постоянном объеме);
– Изобарный (при постоянном давлении);
– Изотермический (при постоянной
температуре);
– Адиабатный (без теплообмена с окружающей
средой)
ПОЛИТРОПНЫЙ ПРОЦЕСС – Обобщенный процесс

4. Политропный процесс

• Постоянство теплоемкости определяет
закономерность изменения параметров в
политропном процессе.
Изохорный, изобарный, изотермический и
адиабатный процессы –
политропные процессы.

5. Показатель политропы

Первый закон термодинамики:
(c-cp)dT = - vdp,
• q=cdT=dh-vdp=cpdT-vdp;
• q=cdT=du+pdv=cvdT+pdv.
(c-cv)dT = pdv .
c cp
vdp
c cv
pdv
n
c cp
c cv
pvn = const

6. Взаимосвязь основных параметров

Tv n 1 const
Tp
1 n
n
const

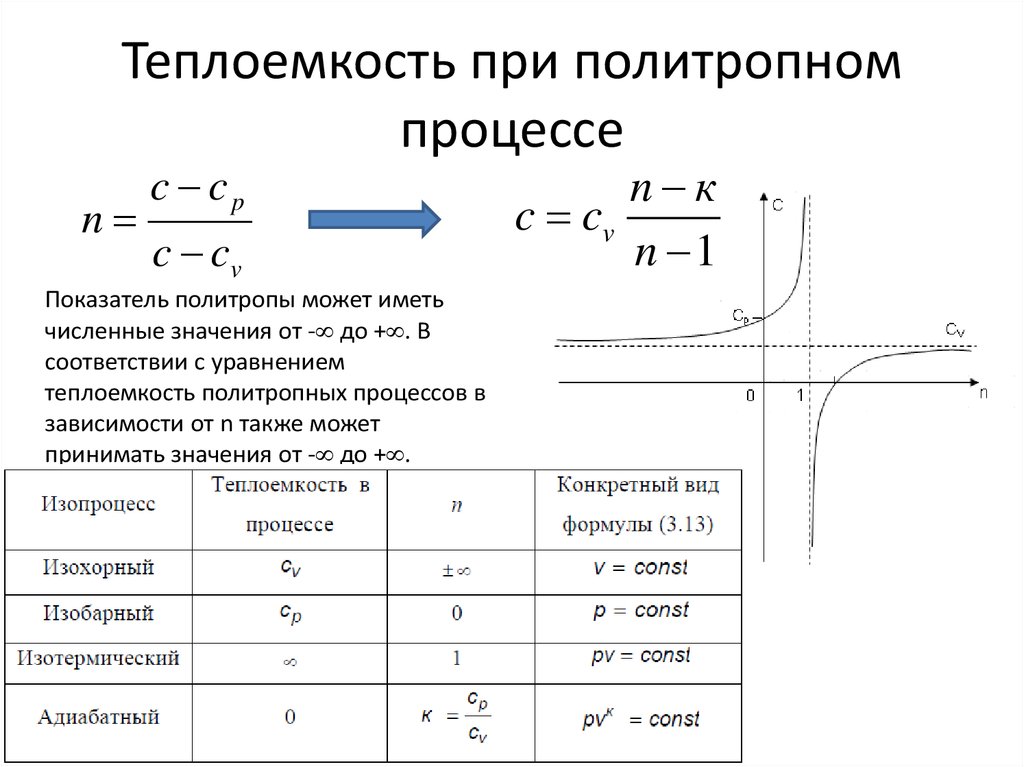
7. Теплоемкость при политропном процессе

n
c cp
c cv
Показатель политропы может иметь
численные значения от - до + . В
соответствии с уравнением
теплоемкость политропных процессов в
зависимости от n также может
принимать значения от - до + .
n к
c cv
n 1

8. Изменение основных параметров

.
Изменение внутренней энергии
u2 - u1 = cv(T2 - T1)
Изменение энтальпии
h2 - h1 = cp(T2 - T1)
Изменение энтропии
cdT
T
n к T2
s2 s1
c ln 2 cv
ln
T
T1
n 1 T1
1
2
Количество теплоты
2
q Tds c(T2 T1 ) cv
1
n к
(T2 T1 )
n 1
Работа
2
l pdv q (u2 u1 ) cv
1
n к
1 к
R
R
T
(T2 T1 ) cv (T2 T1 ) cv
(T2 T1 )
(T1 T2 )
T1 (1 2 )
n 1
n 1
n 1
n 1
T1

9. Частные случаи политропного процесса

.
Изобарный процесс
p
протекает при постоянном давлении.
p=const.
Политропа превращается в изобару при n=0.
Уравнение Tvn-1 = const, при n=0 превращается
в уравнение T/v=const.
n=0
Изменение внутренней энергии u2 - u1 = cv(T2 - T1);
Изменение энтальпии h2 - h1 = cp(T2 - T1) = qp;
Изменение энтропии s2 s1 c p ln
Количество теплоты
T2
v
c p ln 2
T1
v1
qp = cp(T2-T1) = h2-h1
2
Работа изменения объема l p pdv p(v2 v1 ) R(T2 T 1)
1
v

10. Частные случаи политропного процесса

.
Изохорный процесс
p
n=
протекает при постоянном объеме. v=const.
Политропа превращается в изохору при n= .
Уравнение Tp(1-n)/n = const, при n=
превращается в уравнение T/p=const.
n=0
Изменение внутренней энергии u2 - u1 = cv(T2 - T1);
Изменение энтальпии h2 - h1 = cp(T2 - T1);
Изменение энтропии s2 s1 cv ln
Количество теплоты
T2
p
cv ln 2
T1
p1
qv = cv(T2 - T1) = u2 - u1
2
Работа изменения объема lv pdv 0
1
v

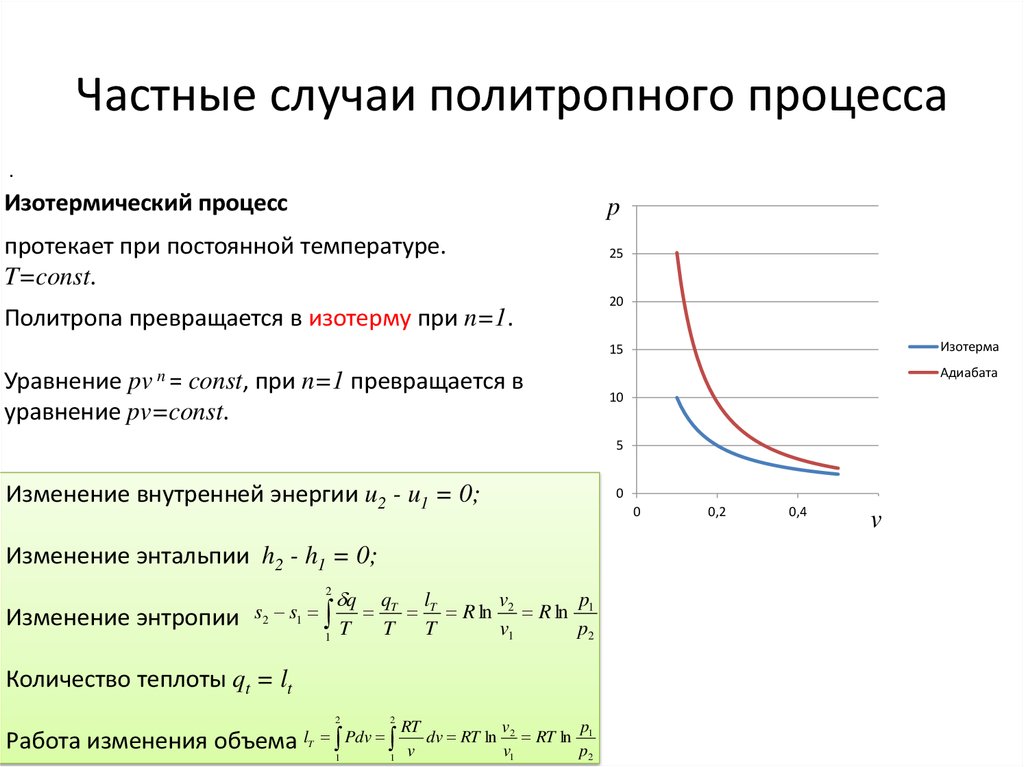
11. Частные случаи политропного процесса

.
Изотермический процесс
p30
протекает при постоянной температуре.
T=const.
Политропа превращается в изотерму при n=1.
25
20
Изотерма
15
Уравнение pv n = const, при n=1 превращается в
уравнение pv=const.
Адиабата
10
5
Изменение внутренней энергии u2 - u1 = 0;
Изменение энтальпии h2 - h1 = 0;
2
Изменение энтропии
s2 s1
1
q
T
qT lT
v
p
R ln 2 R ln 1
T T
v1
p2
Количество теплоты qt = lt
Работа изменения объема l
T
2
2
1
1
Pdv
RT
v
p
dv RT ln 2 RT ln 1
v
v1
p2
0
0
0,2
0,4
0,6
v

12. Частные случаи политропного процесса

.
Адиабатный процесс
p30
протекает без теплообмена. dq=o.
25
Политропа превращается в адиабату при n=k.
20
Изотерма
15
Уравнение pv n = const, при n=k превращается в
уравнение pvk=const.
Адиабата
10
5
Изменение внутренней энергии u2 - u1 = cv(T2 – T1);
Изменение энтальпии h2 - h1 = cp(T2 - T1);
Изменение энтропии ds=0, s=const (изоэнтропный)
Количество теплоты dq = 0
Работа изменения объема ls = - (u2 - u1) = cv(T1 - T2)
0
0
0,2
0,4
0,6
v

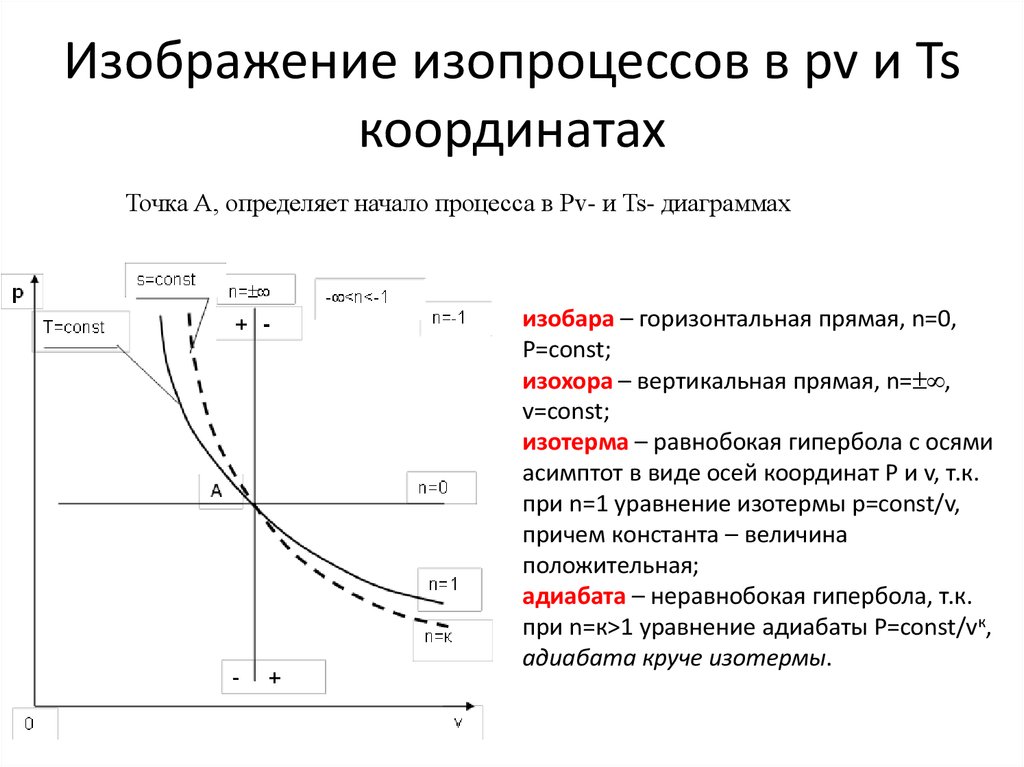
13. Изображение изопроцессов в pv и Ts координатах

Точка А, определяет начало процесса в Рv- и Ts- диаграммах
изобара – горизонтальная прямая, n=0,
Р=const;
изохора – вертикальная прямая, n= ,
v=const;
изотерма – равнобокая гипербола с осями
асимптот в виде осей координат Р и v, т.к.
при n=1 уравнение изотермы p=const/v,
причем константа – величина
положительная;
адиабата – неравнобокая гипербола, т.к.
при n=к>1 уравнение адиабаты Р=const/vк,
адиабата круче изотермы.

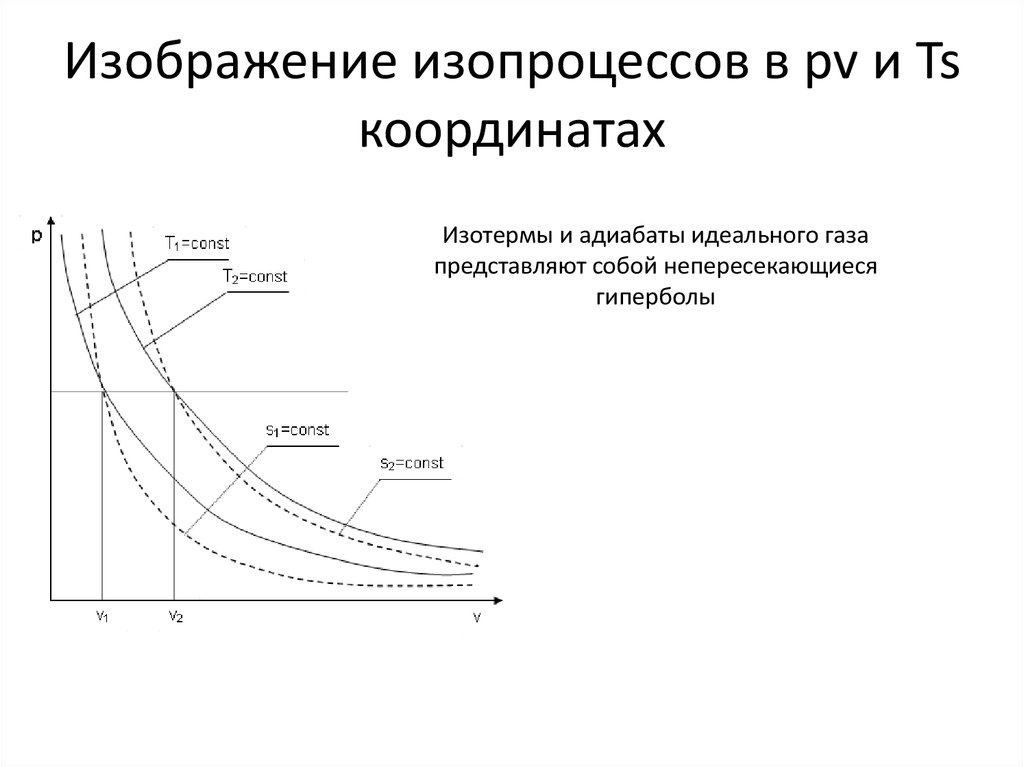
14. Изображение изопроцессов в pv и Ts координатах

Изотермы и адиабаты идеального газа
представляют собой непересекающиеся
гиперболы

15. Изображение изопроцессов в pv и Ts координатах

cdT
T
n к T2
c ln 2 cv
ln
T
T1
n 1 T1
1
2
s2 s1
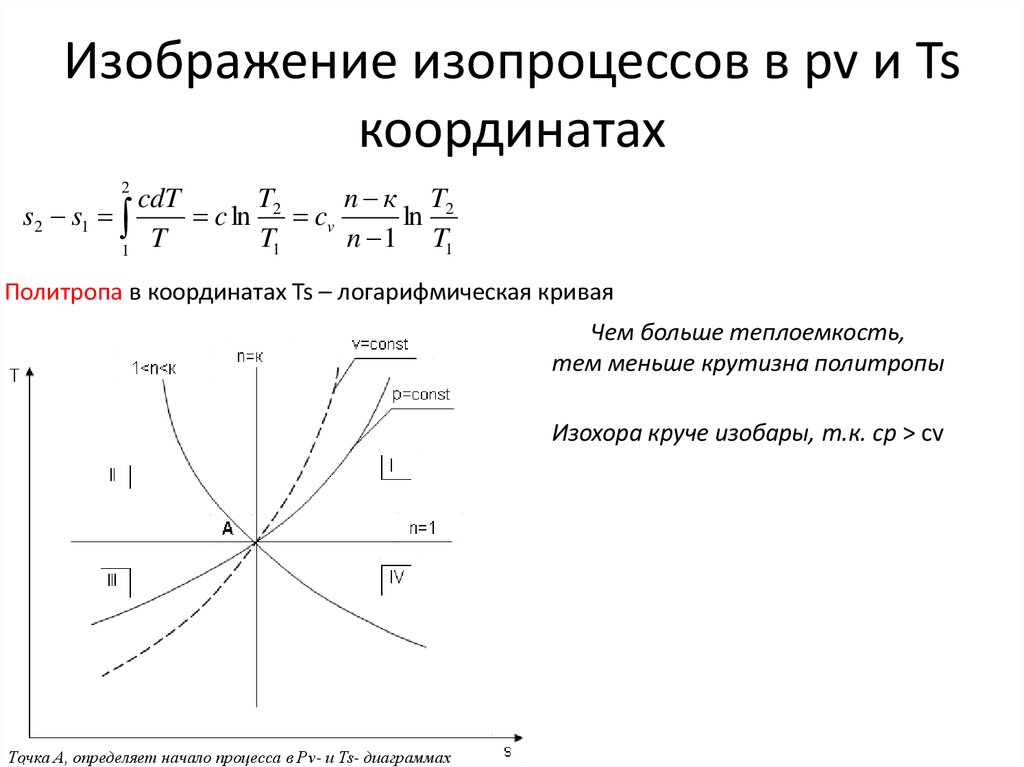
Политропа в координатах Ts – логарифмическая кривая
Чем больше теплоемкость,
тем меньше крутизна политропы
Изохора круче изобары, т.к. cp > cv
Точка А, определяет начало процесса в Рv- и Ts- диаграммах

16. Изображение изопроцессов в pv и Ts координатах

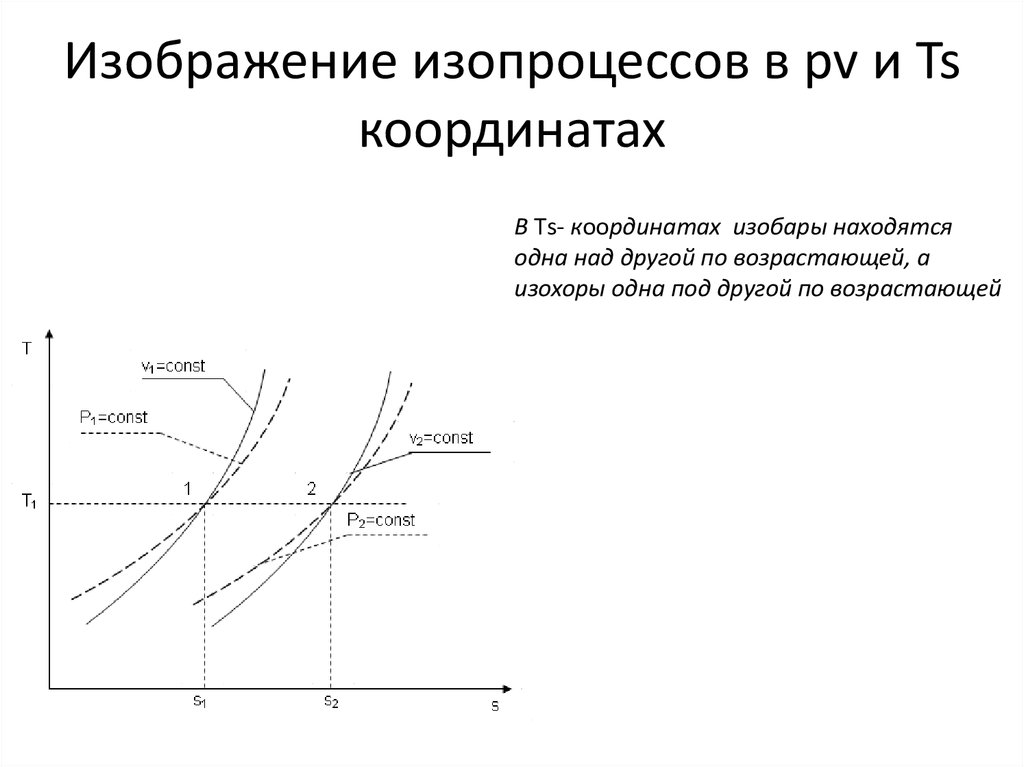
В Тs- координатах изобары находятся
одна над другой по возрастающей, а
изохоры одна под другой по возрастающей

17. Качественный и количественный анализ политропных процессов в Рv- и Ts- диаграммах

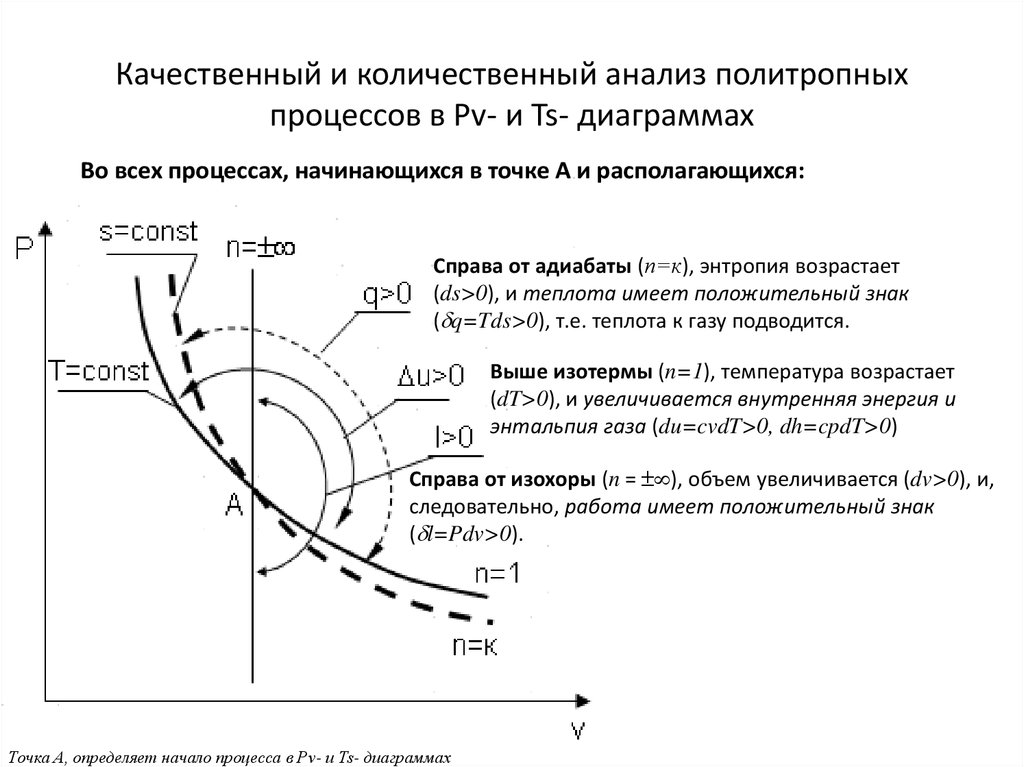
Во всех процессах, начинающихся в точке А и располагающихся:
Cправа от адиабаты (n=к), энтропия возрастает
(ds>0), и теплота имеет положительный знак
( q=Tds>0), т.е. теплота к газу подводится.
Выше изотермы (n=1), температура возрастает
(dT>0), и увеличивается внутренняя энергия и
энтальпия газа (du=cvdT>0, dh=cpdT>0)
Cправа от изохоры (n = ), объем увеличивается (dv>0), и,
следовательно, работа имеет положительный знак
( l=Pdv>0).
Точка А, определяет начало процесса в Рv- и Ts- диаграммах

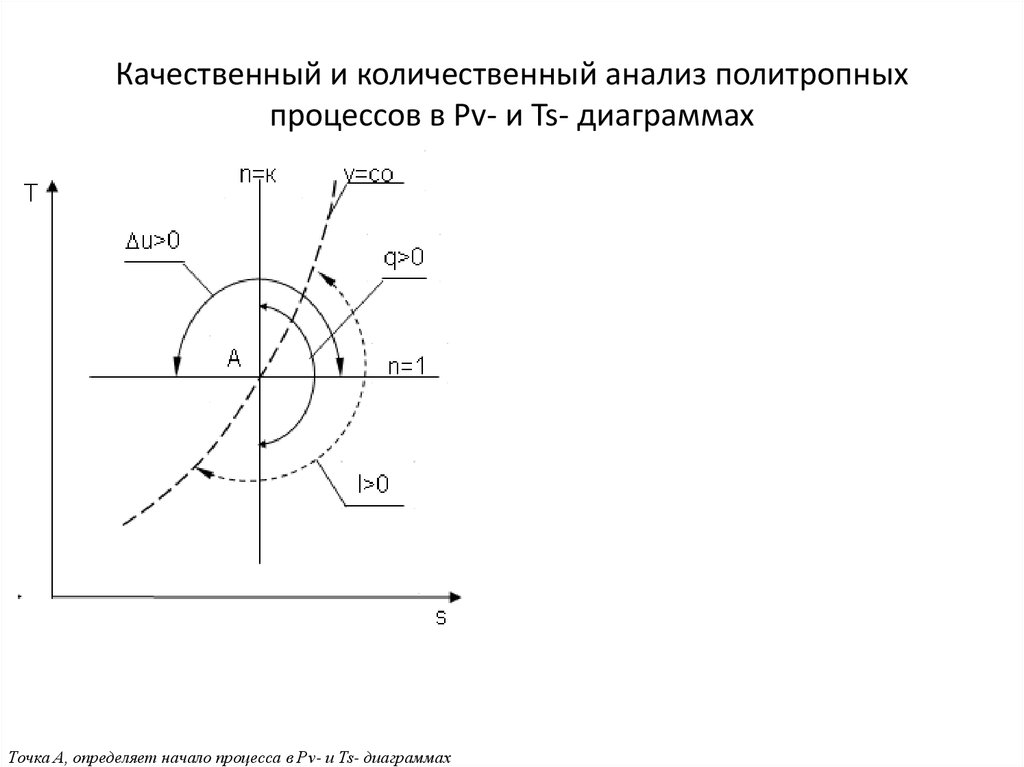
18. Качественный и количественный анализ политропных процессов в Рv- и Ts- диаграммах

Точка А, определяет начало процесса в Рv- и Ts- диаграммах

19. Использование первого закона термодинамики для энергетического анализа круговых   процессов (циклов)

Использование первого закона термодинамики для
энергетического анализа круговых процессов (циклов)
Уравнение первого закона термодинамики для циклов
может быть получено в результате интегрирования dq=du+dl
уравнения по всему контуру цикла:
Qц=Lц
Таким образом, первый закон термодинамики исключает
возможность создания "вечного двигателя" первого рода, то
есть двигателя, который производил бы работу, не требуя
для этого затрат энергии.

20. Использование первого закона термодинамики для энергетического анализа круговых   процессов (циклов)

Использование первого закона термодинамики для
энергетического анализа круговых процессов (циклов)
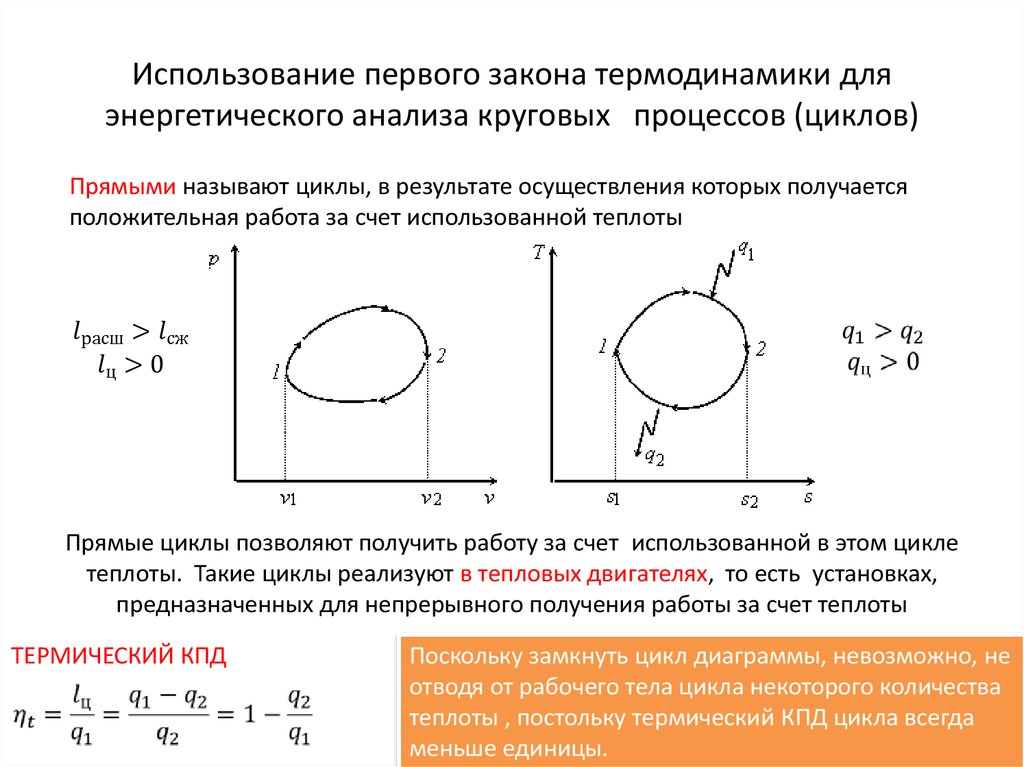
Прямыми называют циклы, в результате осуществления которых получается
положительная работа за счет использованной теплоты
Прямые циклы позволяют получить работу за счет использованной в этом цикле
теплоты. Такие циклы реализуют в тепловых двигателях, то есть установках,
предназначенных для непрерывного получения работы за счет теплоты
ТЕРМИЧЕСКИЙ КПД
Поскольку замкнуть цикл диаграммы, невозможно, не
отводя от рабочего тела цикла некоторого количества
теплоты , постольку термический КПД цикла всегда
меньше единицы.

21. Использование первого закона термодинамики для энергетического анализа круговых   процессов (циклов)

Использование первого закона термодинамики для
энергетического анализа круговых процессов (циклов)
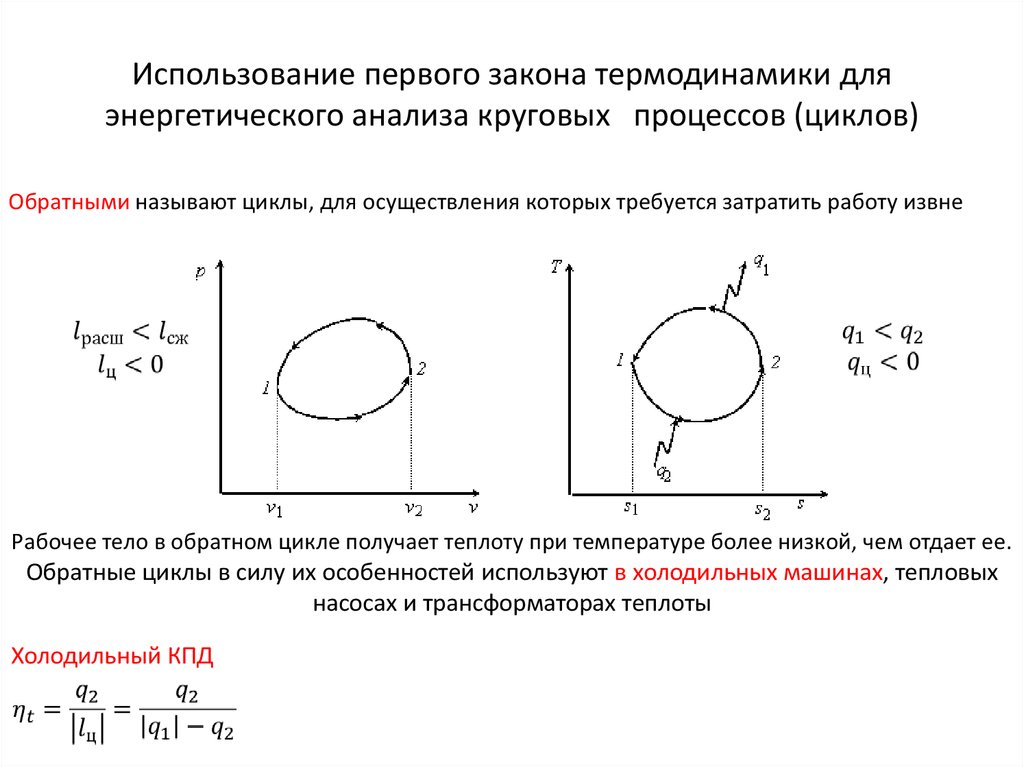
Обратными называют циклы, для осуществления которых требуется затратить работу извне
Рабочее тело в обратном цикле получает теплоту при температуре более низкой, чем отдает ее.
Обратные циклы в силу их особенностей используют в холодильных машинах, тепловых
насосах и трансформаторах теплоты
Холодильный КПД