ТТД 05. Политропные процессы. Энтропия идеального газа. Тепловая Ts-диаграмма

1. ТТД 05

● Политропные процессы
● Энтропия идеального газа
● Тепловая Ts-диаграмма

2. Исследование политропных процессов

1. Уравнение процесса выводится из аналитического
выражения I закона термодинамики:
dq=du+pdv; cdT=cvdT+pdv; (c-cv)dT-pdv=0.
Сделаем подстановку из уравнения Клапейрона
pv=RT; T=pv/R; dT=(pdv+vdp)/R.
После подстановки dT в (1) имеем:
(c-cv)(pdv+vdp)/R-pdv=0.
(1)

3. Преобразование выражения I закона термодинамики

Умножим полученное выражение на R/(c-cv):
pdv+vdp-Rpdv/(c-cv)=0.
С учетом уравнения Майера R=cp-cv:
pdv+vdp-(cp-cv)pdv/(c-cv)=0.
После приведения подобных членов и сокращения имеем:
[1-(cp-cv)/(c-cv)]pdv+vdp=npdv+vdp=0.

4. Уравнение политропных процессов

Разделим переменные, поделив уравнение на pv:
ndv/v+dp/p=0.
После интегрирования при n=Const:
nlnv+lnp=Const;
или:
ln(pvn)=ln(Const).
После потенцирования получаем уравнение политропных
процессов:
pvn=Const.

5. Соотношения между параметрами

На предыдущем слайде за показатель политропы принято
выражение:
n =[1-(cp-cv)/(c-cv)]= (c-cp)/(c-cv).
2. pv-диаграмму политропных процессов рассмотрим позже.
3. Поскольку уравнение политропы pvn=Const аналогично
уравнению адиабаты pvk=Const, то все соотношения
между параметрами будут аналогичные:
p1v1n=p2v2n; T2/T1=(v1/v2)n-1; T2/T1=(p2/p1)(n-1)/n.

6. Работа и теплота

4. Изменение внутренней энергии: Δu=cvΔT.
5. Выражения для работы также запишутся по аналогии с
адиабатным процессом:
l=(p1v1-p2v2)/(n-1); l=(T1-T2)R/(n-1).
6. Теплота по I закону термодинамики:
q=Δu+l.
и через теплоемкость:
q=cΔT.

7. Показатель политропы и энергетический коэффициент

Политропную теплоемкость можно найти из выражения
показателя политропы:
n=(c-cp)/(c-cv); nc-ncv=c-cp;
приводим подобные члены, умножая и деля выражение на cv
и учитывая, что cp/cv=k:
c=(ncv-cp)cv/(n-1)cv=(n-k)cv/(n-1).
7. Энергетический коэффициент:
φ=Δu/q=cvΔT/[(n-k)cvΔT/(n-1)];
или:
φ=(n-1)/(n-k).

8. Обобщающее значение политропных процессов

Уравнение политропных процессов pvn=Const справедливо
для любого из частных термодинамических процессов:
● изохорный
n=∞: p1/nv=p1/∞v=p0v=v=Const;
● изобарный
n=0: pv0=p=Const;
● изотермический
n=1: pv=Const или T=Const;
● адиабатный
n=k: pvk=Const.

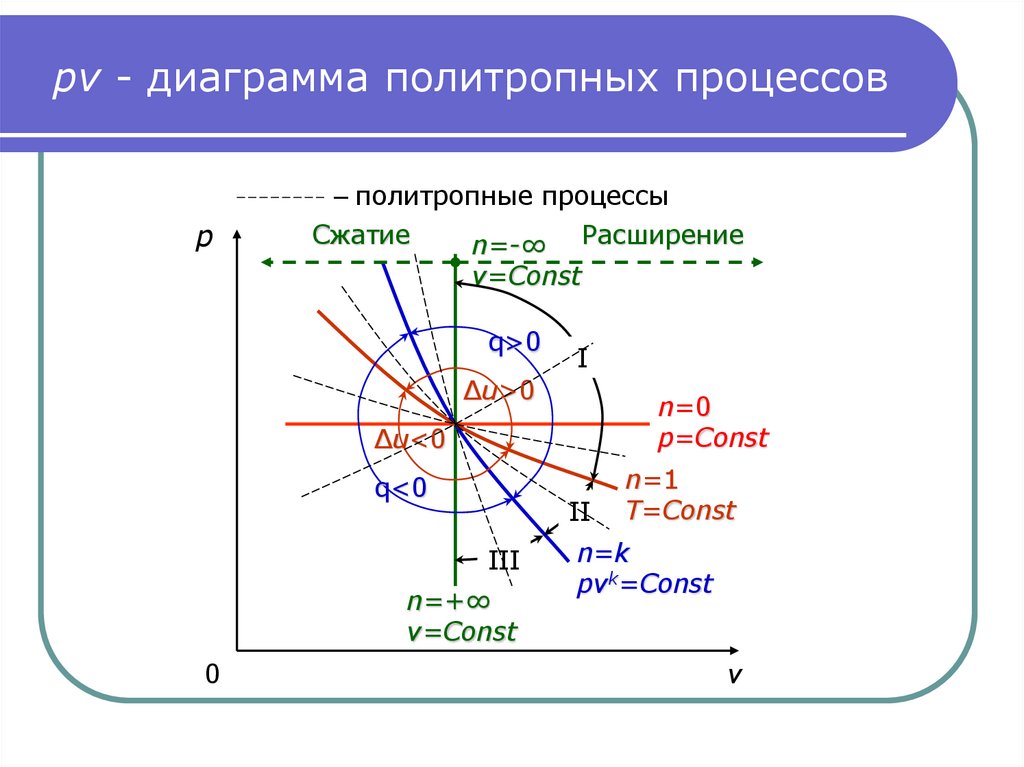
9. Три группы политропных процессов

На следующем слайде изображены все возможные
термодинамические процессы.
Изотерма T=Const разделяет их на две группы:
Δu>0 и Δu<0.
Адиабата также делит их на две группы:
q>0 и q<0.
Таким образом, по знакам изменения внутренней энергии и
теплоты процессы расширения газа делятся на I, II и III
группы.

10. pv - диаграмма политропных процессов

– политропные процессы
p
Сжатие
n=-∞ Расширение
v=Const
q>0
I
Δu>0
n=0
p=Const
Δu<0
q<0
II
III
n=+∞
v=Const
0
n=1
T=Const
n=k
pvk=Const
v

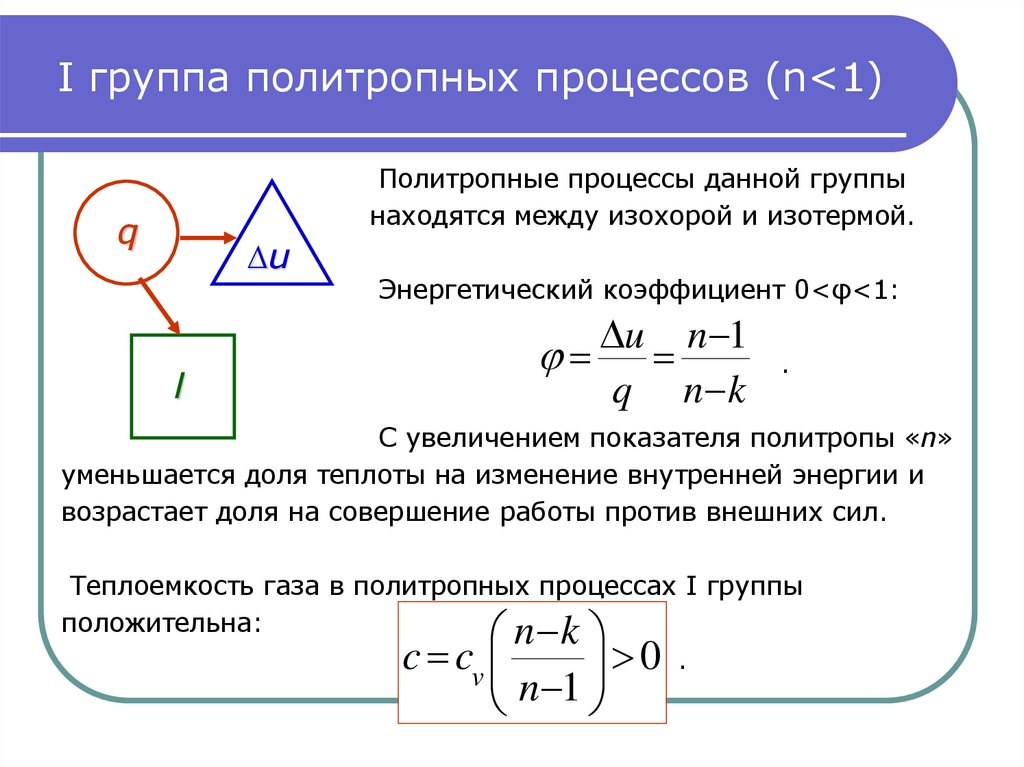
11. I группа политропных процессов (n<1)

I группа политропных процессов (n<1)
Политропные процессы данной группы
находятся между изохорой и изотермой.
q
∆u
l
Энергетический коэффициент 0<φ<1:
u n 1
q
n k
.
С увеличением показателя политропы «n»
уменьшается доля теплоты на изменение внутренней энергии и
возрастает доля на совершение работы против внешних сил.
Теплоемкость газа в политропных процессах I группы
положительна:
.
n k
c cv
0
n 1

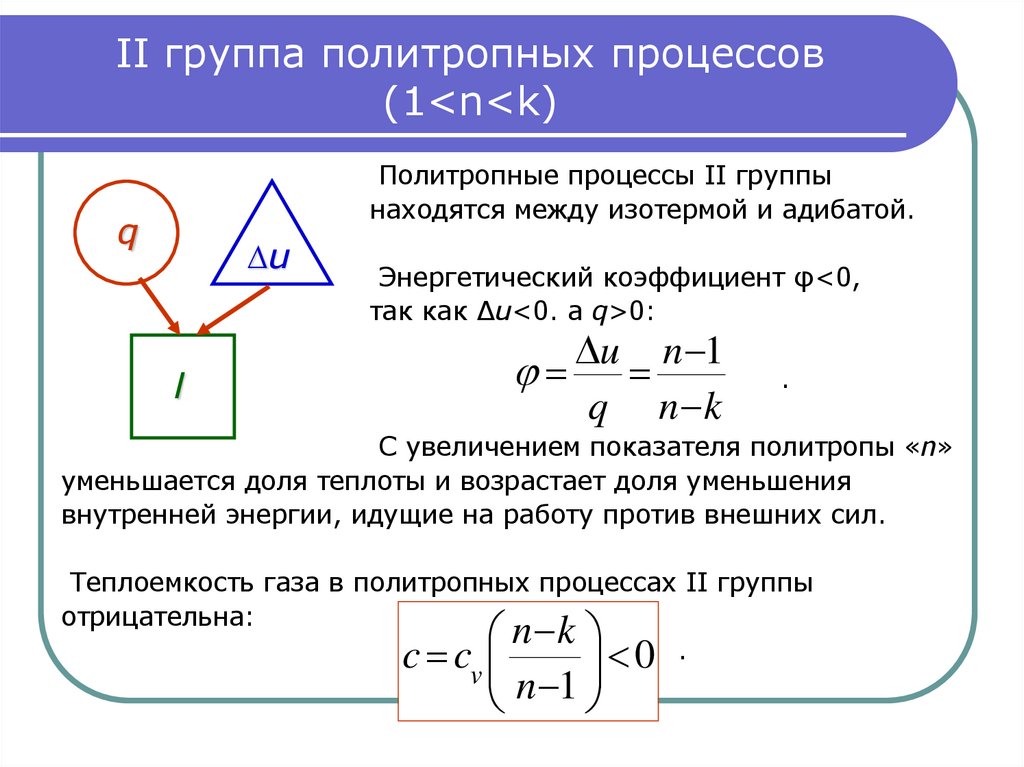
12. II группа политропных процессов (1<n<k)

II группа политропных процессов
(1<n<k)
Политропные процессы II группы
находятся между изотермой и адибатой.
q
∆u
Энергетический коэффициент φ<0,
так как ∆u<0. а q>0:
u n 1
l
q
n k
.
С увеличением показателя политропы «n»
уменьшается доля теплоты и возрастает доля уменьшения
внутренней энергии, идущие на работу против внешних сил.
Теплоемкость газа в политропных процессах II группы
отрицательна:
n k
c c
0 .
v
n
1

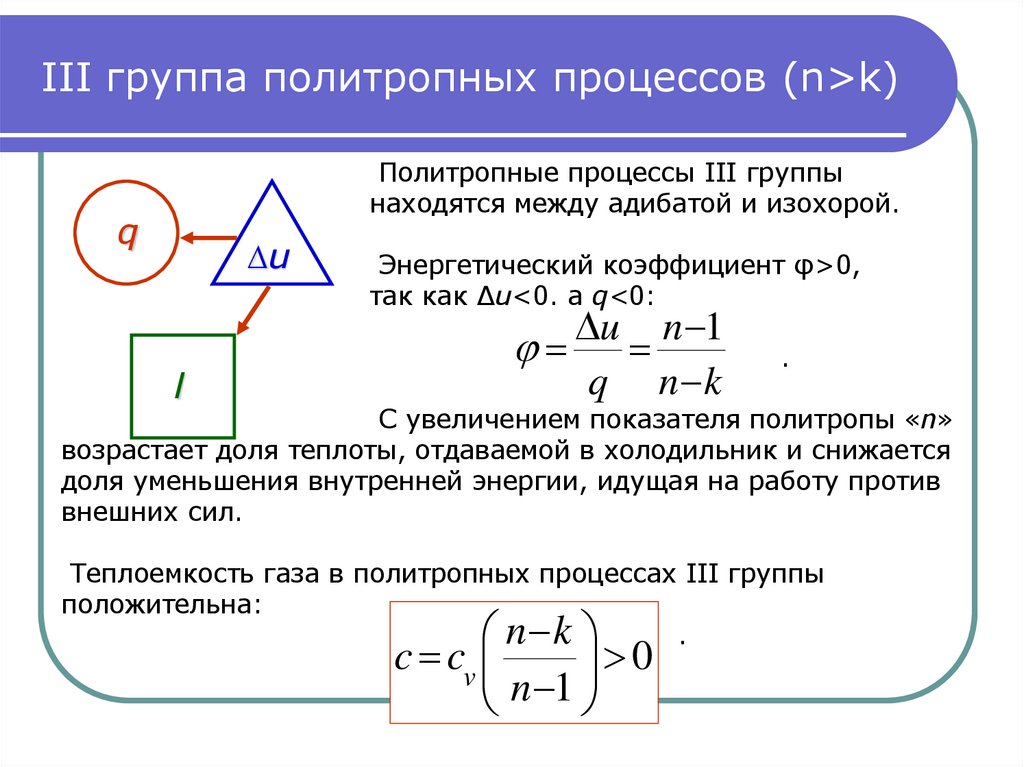
13. III группа политропных процессов (n>k)

III группа политропных процессов (n>k)
Политропные процессы III группы
находятся между адибатой и изохорой.
q
∆u
l
Энергетический коэффициент φ>0,
так как ∆u<0. а q<0:
u n 1
q n k
.
С увеличением показателя политропы «n»
возрастает доля теплоты, отдаваемой в холодильник и снижается
доля уменьшения внутренней энергии, идущая на работу против
внешних сил.
Теплоемкость газа в политропных процессах III группы
положительна:
.
n k
c cv
0
n 1

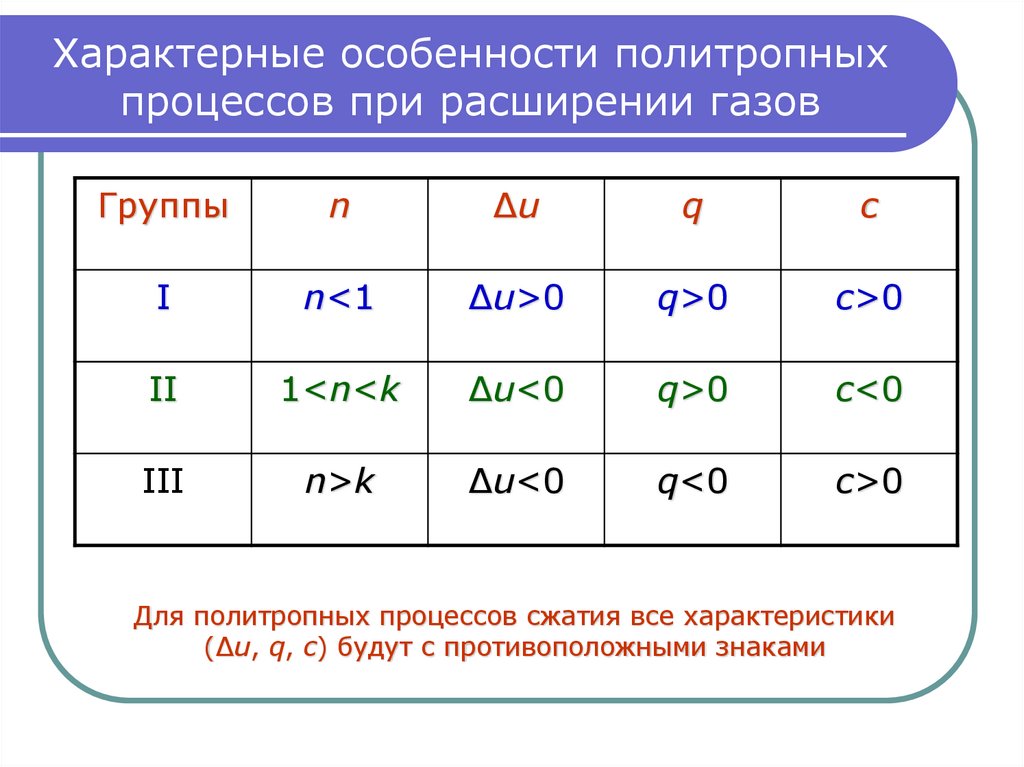
14. Характерные особенности политропных процессов при расширении газов

Группы
n
∆u
q
c
I
n<1
∆u>0
q>0
c>0
II
1<n<k
∆u<0
q>0
c<0
III
n>k
∆u<0
q<0
c>0
Для политропных процессов сжатия все характеристики
(∆u, q, c) будут с противоположными знаками

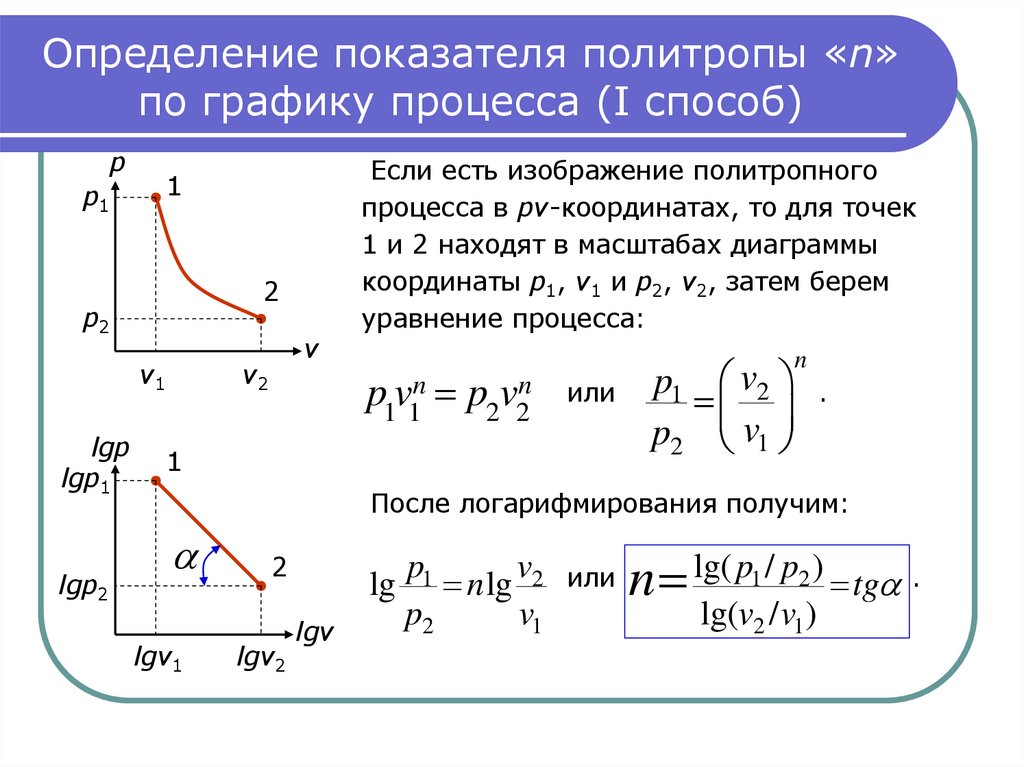
15. Определение показателя политропы «n» по графику процесса (I способ)

р
1
p1
2
p2
v1
lgp
lgp1
lgp2
v
v2
Если есть изображение политропного
процесса в pv-координатах, то для точек
1 и 2 находят в масштабах диаграммы
координаты p1, v1 и p2, v2, затем берем
уравнение процесса:
p1v1n p2v2n
1
n
или
p1 v2 .
p2 v1
После логарифмирования получим:
lgv1
2
lgv2
lg
lgv
lg( p1 / p2 )
p1
v
n lg 2 или n
tg .
lg(v2 / v1)
p2
v1

16. II способ определения показателя политропы «n»

р
А
C
v
D
В
L
E
v
Для произвольной точки С , из которой
проведена подкасательная СЕ к
политропному процессу АВ:
tg (dp / dv) .
Найдем производную dp/dv из уравнения
политропы pvn=const.
Дифференцируем уравнение политропы:
vndp npvn 1dv 0 ,
откуда:
tg
dp npv n 1 np
n
dv
v
v
.
(1)

17. Формулировка II способа

С учетом (1), из прямоугольного треугольника CDE имеем:
CD p np
tg
n
DE L v
.
Таким образом, показатель политропы «n» численно равен
абсциссе v произвольной точки С , поделенной на длину
подкасательной L для этой точки.

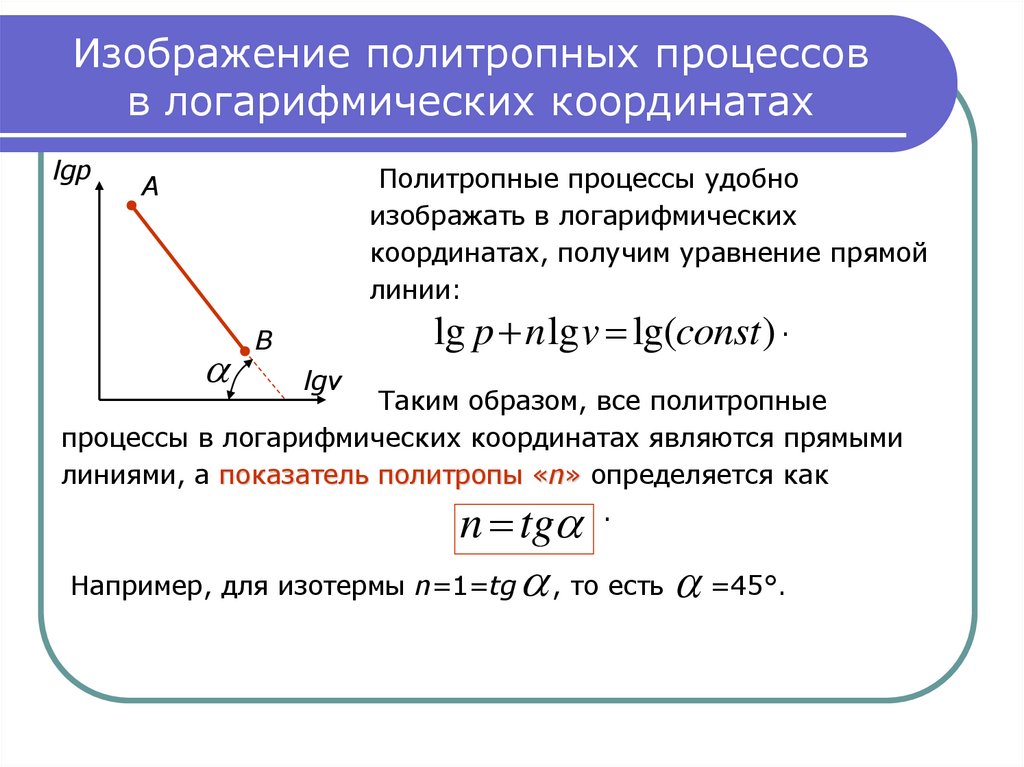
18. Изображение политропных процессов в логарифмических координатах

lgp
Политропные процессы удобно
изображать в логарифмических
координатах, получим уравнение прямой
линии:
lg p n lg v lg(const ) .
A
B
lgv
Таким образом, все политропные
процессы в логарифмических координатах являются прямыми
линиями, а показатель политропы «n» определяется как
.
n tg
Например, для изотермы n=1=tg
, то есть =45°.

19. Энтропия идеального газа

Обозначим через дифференциал энтропии выражение
ds=dq/T, Дж/(кгК).
(1)
Тогда теплоту можно определить как dq=Tds, то есть
площадь под процессом в Ts-диаграмме.
Найдем зависимости T=f(s) для термодинамических
процессов подстановкой в (1) I закона термодинамики:
ds du pdv cv dT pdv cv dT R dv ;
(2)
c dT vdp
(3)
T
T
ds dh vdp p
T
T
T
v
c p dT R dp .
T
p

20. Изменение энтропии в термодинамических процессах

Проинтегрировав выражения (2) и (3), получим изменения
энтропии в политропных процессах:
s cv n T2 R n v2 ; (4)
T1
v1
s cp n T2 R n p2
T1
.
(5)
p1
Из (4) при v=Const и из (5) при p=Const получим
изменения энтропии в изохорном и изобарном процессах:
sv cv n T2 ; (6)
T1
s p cp n T2 .
T1
(7)

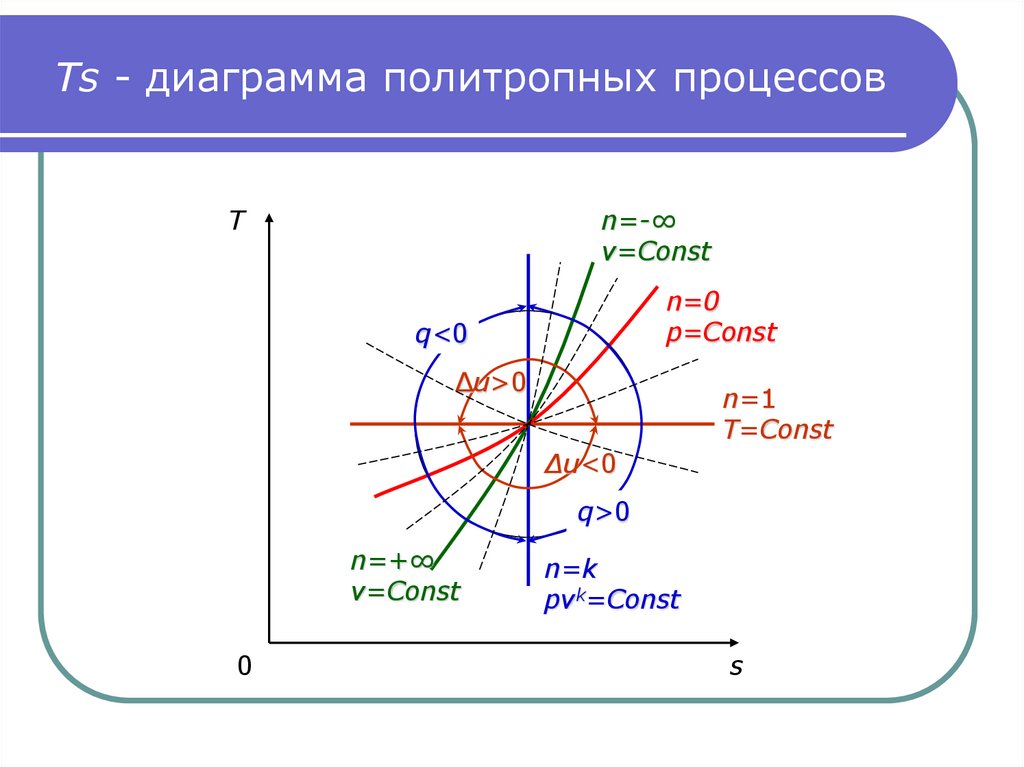
21. Изображение термодинамических процессов в Ts-диаграмме

Из выражений (6, 7) следует, что изохора и изобара в Tsдиаграмме представляют собой логарифмические кривые.
Причем изохора проходит круче изобары, так как
при ΔT=idem:
Δsp>Δsv из-за cp>cv.
Изотерма в Ts-диаграмме отображается горизонтальной
прямой.
Изображение адиабаты вытекает из анализа выражения
dq=0=Tds.

22. Изотерма и адиабата в Ts-диаграмме

Так как T≠0, то ds=0, следовательно s=Const – это и
есть уравнение адиабаты в Ts-диаграмме.
На следующем слайде представлена Ts-диаграмма
термодинамических процессов.
Площадь под процессом в Ts-диаграмме представляет
собой теплоту, поэтому она называется тепловой диаграммой.

23. Ts - диаграмма политропных процессов

T
n=-∞
v=Const
n=0
p=Const
q<0
Δu>0
n=1
T=Const
Δu<0
q>0
n=+∞
v=Const
0
n=k
pvk=Const
s