Кибернетические системы

1. Лекция 4. Кибернетические системы

Содержание лекции:
1.
Понятие кибернетической системы
2.
Закон необходимого разнообразия
3.
Кибернетическая система как форма представления систем
Кибернетические системы
© Н.М. Светлов, 2006-2010
1/11

2. Литература

1. Понятие кибернетической системы
• Система управления, или кибернетическая система,
характеризуется:
– целью управления;
– объектом управления (управляемой подсистемой);
– функцией управления:
• оптимизация
• стабилизация
• слежение (мониторинг);
– факторами неопределённости
• Процесс управления можно представить как процесс
снятия энтропии управляемой подсистемы воздействием
со стороны управляющей подсистемы
Кибернетические системы
© Н.М. Светлов, 2006-2010
3/11

3. 1. Понятие кибернетической системы

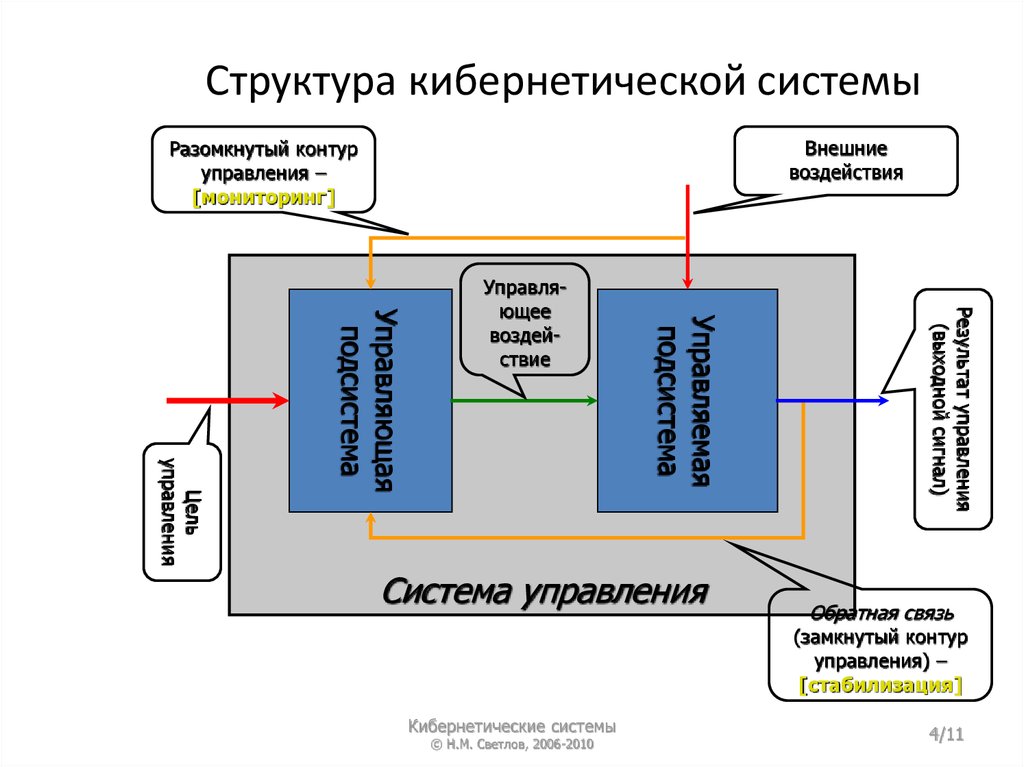
Структура кибернетической системы
Внешние
воздействия
Разомкнутый контур
управления –
[мониторинг]
Система управления
Результат управления
(выходной сигнал)
Управляемая
подсистема
Цель
управления
Управляющая
подсистема
Управляющее
воздействие
Обратная связь
(замкнутый контур
управления) –
[стабилизация]
Кибернетические системы
© Н.М. Светлов, 2006-2010
4/11

4. Структура кибернетической системы

1. Понятие
кибернетической системы
Характеристики системы управления
Управляемость
• характеристика системы управления, отражающая способность управляющей подсистемы
снижать энтропию управляемой подсистемы
• может быть охарактеризована долей снятой энтропии в общей энтропии управляемой
подсистемы (до акта управления)
• находится в обратной зависимости со сложностью управляемой подсистемы
Достижимость
• характеристика системы управления, решающей задачу оптимизации
• отражает способность управляющей подсистемы достичь требуемых характеристик
выходного сигнала
• выражается показателями эффективности:
• отношение выходного сигнала к значению некоторой входной переменной;
• отношение достигнутого выходного сигнала к его оптимальному значению.
Устойчивость
• характеристика системы управления, решающей задачу стабилизации
• отражает способность управляющей подсистемы поддерживать характеристики
выходного сигнала, задаваемые целью управления
• может быть выражена:
• абсолютным либо относительным отклонением от заданного значения;
• вероятностью выхода за пределы заданного диапазона
Кибернетические системы
© Н.М. Светлов, 2006-2010
5/11

5. 1. Понятие кибернетической системы

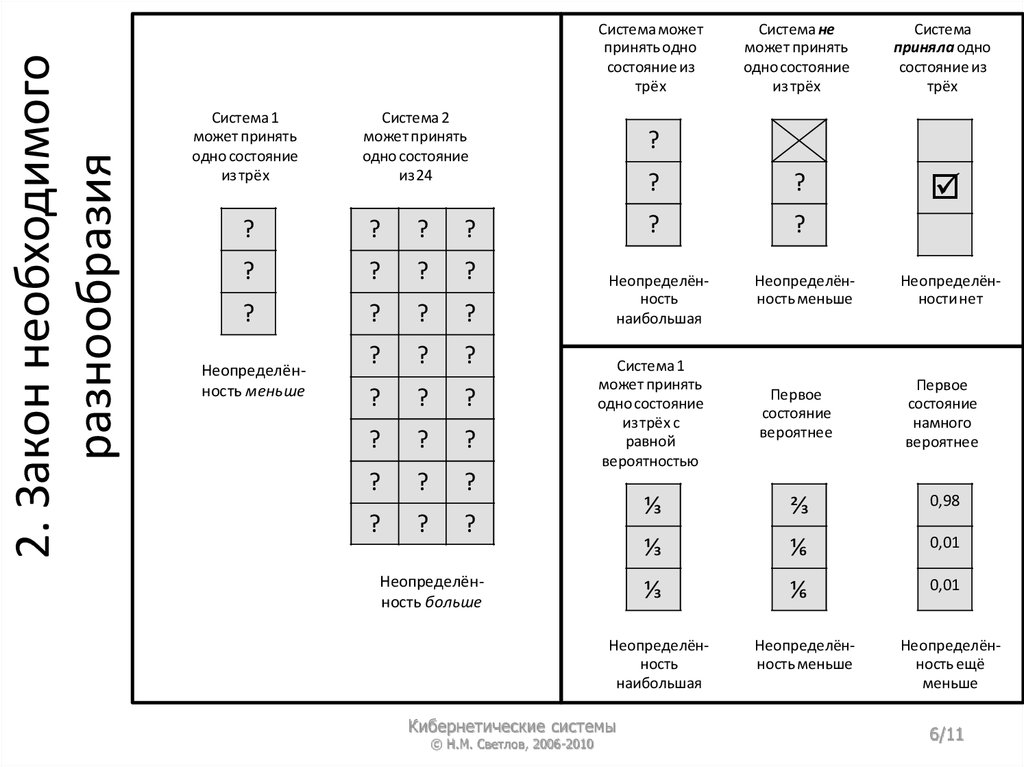
2. Закон необходимого
разнообразия
Система может
принять одно
состояние из
трёх
Система 1
может принять
одно состояние
из трёх
Система 2
может принять
одно состояние
из 24
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
Неопределённость меньше
Система не
может принять
одно состояние
из трёх
Система
приняла одно
состояние из
трёх
?
?
?
?
?
Неопределённость
наибольшая
Неопределённость меньше
Неопределённости нет
Система 1
может принять
одно состояние
из трёх с
равной
вероятностью
Первое
состояние
вероятнее
Первое
состояние
намного
вероятнее
⅓
⅔
0,98
⅓
⅙
0,01
⅓
⅙
0,01
Неопределённость больше
Неопределённость
наибольшая
Кибернетические системы
© Н.М. Светлов, 2006-2010
Неопределённость меньше
Неопределённость ещё
меньше
6/11

6. 2. Закон необходимого разнообразия

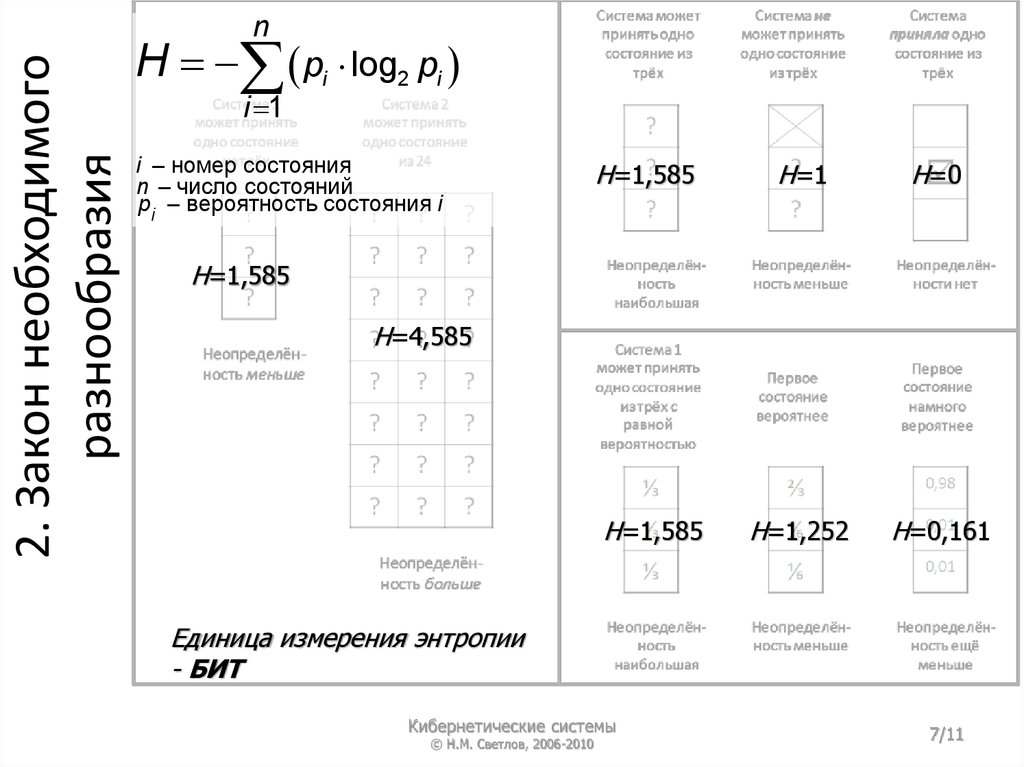
n
H pi log2 pi
i 1
i – номер состояния
n – число состояний
pi – вероятность состояния i
H=1,585
H=1
H=0
H=1,252
H=0,161
H=1,585
H=4,585
H=1,585
Единица измерения энтропии
- БИТ
Кибернетические системы
© Н.М. Светлов, 2006-2010
7/11

7. 2. Закон необходимого разнообразия

Если состояния системы равновероятны, то H=log2 N,
где N – число состояний системы
Энтропия объединённой системы:
• равна сумме энтропий её подсистем, если подсистемы
независимы
• меньше суммы энтропий подсистем, если подсистемы влияют
друг на друга
Если известно, в каком состоянии находится система,
её энтропия равна нулю
Кибернетические системы
© Н.М. Светлов, 2006-2010
8/11

8. 2. Закон необходимого разнообразия

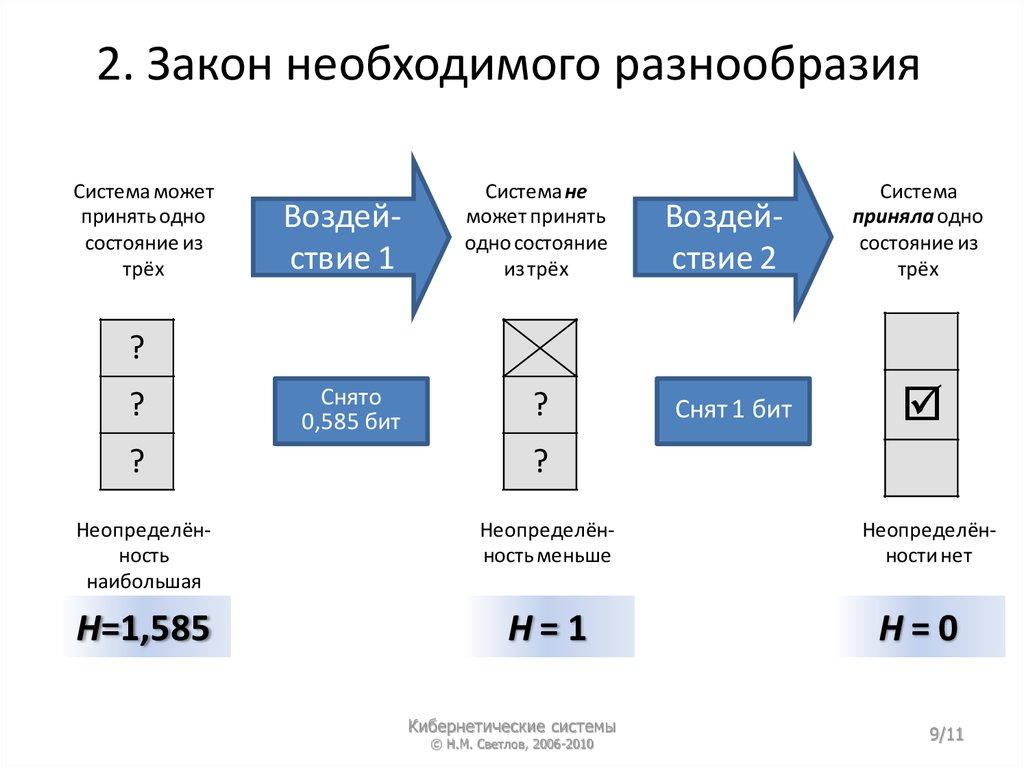
Система может
принять одно
состояние из
трёх
Воздействие 1
Система не
может принять
одно состояние
из трёх
Воздействие 2
Система
приняла одно
состояние из
трёх
?
?
?
Снято
0,585 бит
?
Снят 1 бит
?
Неопределённость
наибольшая
Неопределённость меньше
H=1,585
H=1
Кибернетические системы
© Н.М. Светлов, 2006-2010
Неопределённости нет
H=0
9/11

9. 2. Закон необходимого разнообразия

Энтропия управляемой подсистемы может быть снята
полностью лишь в том случае, если энтропия
управляющей подсистемы не меньше энтропии
управляемой подсистемы (У. Эшби)
Менее сложная система не может полностью
контролировать более сложную
Кибернетические системы
© Н.М. Светлов, 2006-2010
10/11

10. 2. Закон необходимого разнообразия

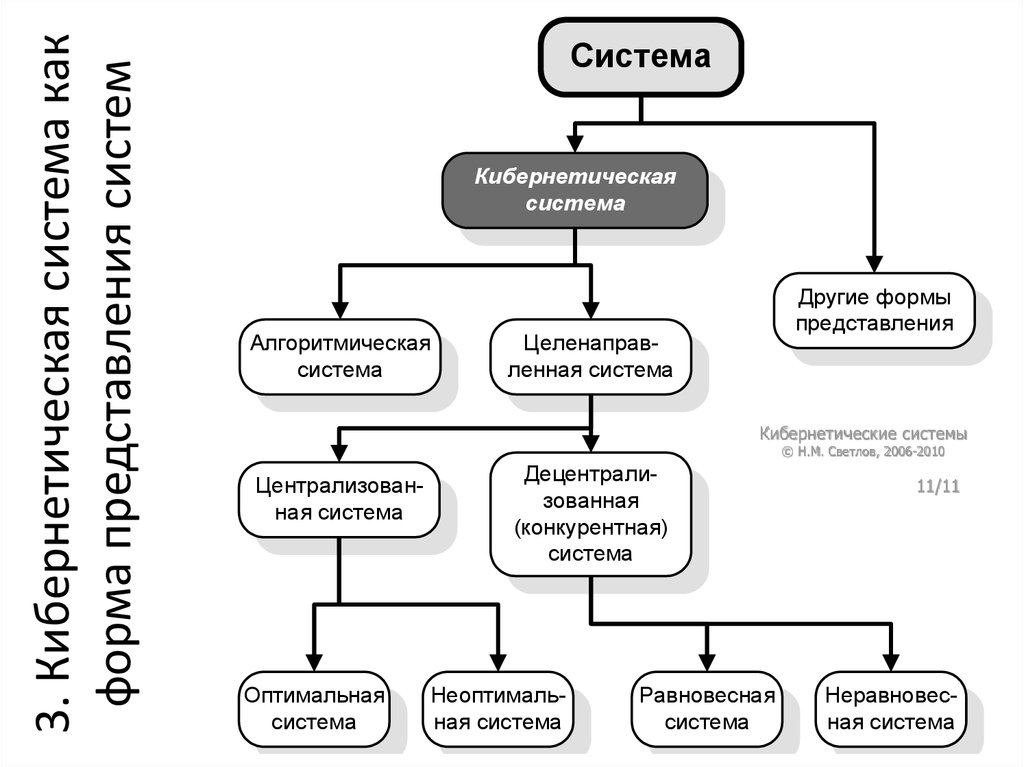
3. Кибернетическая система как
форма представления систем
Система
Кибернетическая
система
Алгоритмическая
система
Другие формы
представления
Целенаправленная система
Кибернетические системы
© Н.М. Светлов, 2006-2010
Централизованная система
Оптимальная
система
Децентрализованная
(конкурентная)
система
Неоптимальная система
Равновесная
система
11/11
Неравновеcная система