Кибернетические системы. Лекция 3

1. Лекция 3. Кибернетические системы

Содержание лекции:
1.
Энтропия и информация
2.
Понятие «кибернетическая система»
3.
Структура кибернетической системы
4.
Закон необходимого разнообразия
5.
Функции управления
Кибернетические системы
© Н.М. Светлов, 2006-2011
1/11

2. Литература

1.
2.
3.
4.
Сурмин Ю.П. Теория систем и системный
анализ: Учебное пособие. Киев: МАУП, 2003.
Винер Н. Кибернетика, или управление и связь в
животном и машине. М.: Наука, 1983.
Винер Н. Кибернетика и общество. М.: Тайдекс
Ко, 2002.
Бир С. Мозг фирмы. М.: Горячая линия –
Телеком, 1993.
Кибернетические системы
© Н.М. Светлов, 2006-2011
2/11

3. 1. Энтропия и информация

Мера неопределённости
состояния системы называется
энтропией
Энтропия измеряется в битах
1 бит – это энтропия системы,
способной принимать два
состояния с равной
вероятностью
Величина энтропии в битах
равна двоичному логарифму
числа её возможных
состояний, если они
равновероятны
Если система состоит из N
элементов, каждый из которых
принимает два состояния с
равной вероятностью, то её
энтропия равна N бит
В общем случае энтропия
(в битах) равна
pi log 2 ( pi ), если pi 0;
i 1 0, если pi 0
n число состояний системы
n
pi
Кибернетические системы
© Н.М. Светлов, 2006-2011
вероятность состояния
3/11
i

4.

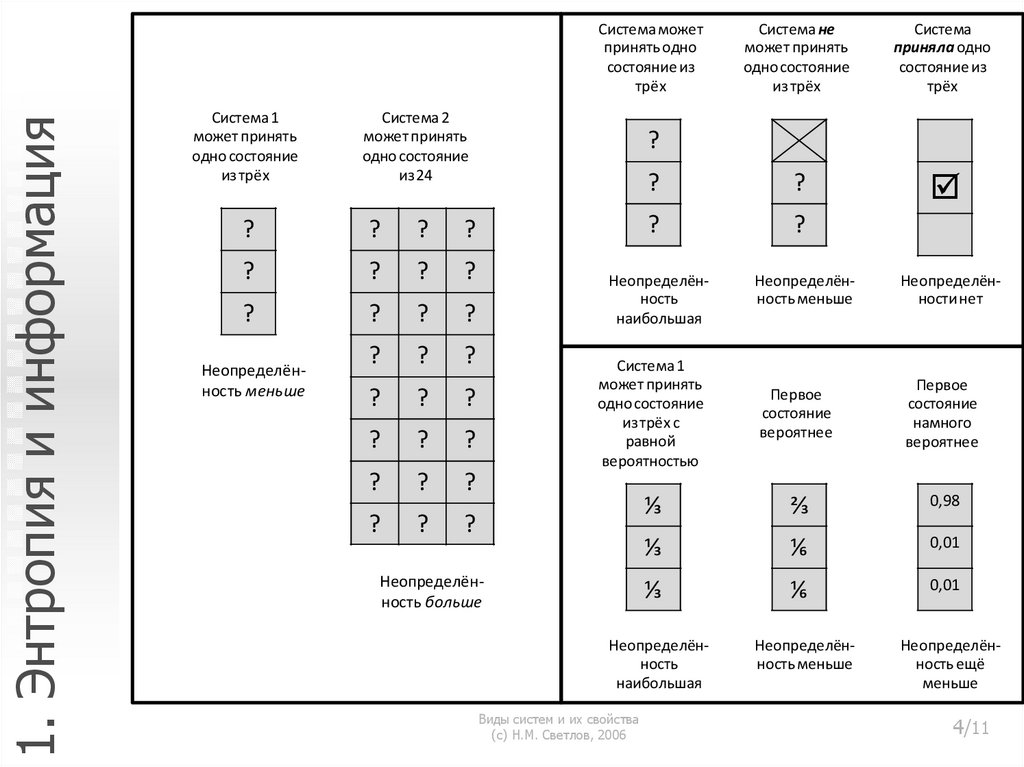
1. Энтропия и информация
Система может
принять одно
состояние из
трёх
Система 1
может принять
одно состояние
из трёх
Система 2
может принять
одно состояние
из 24
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
Неопределённость меньше
Система не
может принять
одно состояние
из трёх
Система
приняла одно
состояние из
трёх
?
?
?
?
?
Неопределённость
наибольшая
Неопределённость меньше
Неопределённости нет
Система 1
может принять
одно состояние
из трёх с
равной
вероятностью
Первое
состояние
вероятнее
Первое
состояние
намного
вероятнее
⅓
⅔
0,98
⅓
⅙
0,01
⅓
⅙
0,01
Неопределённость больше
Неопределённость
наибольшая
Виды систем и их свойства
(с) Н.М. Светлов, 2006
Неопределённость меньше
Неопределённость ещё
меньше
4/11

5.

n
1. Энтропия и информация
H pi log2 pi
i 1
i – номер состояния
n – число состояний
pi – вероятность состояния i
H=1,585
H=1
H=0
H=1,252
H=0,161
H=1,585
H=4,585
H=1,585
Единица измерения энтропии
- БИТ
Виды систем и их свойства
(с) Н.М. Светлов, 2006
5/11

6. 1. Энтропия и информация

Если благодаря некоторому событию состояние
системы, энтропия которой составляла x бит,
стало нам известно, то:
её энтропия стала равна
нулю
мы получили о ней x бит
информации
• система теперь достоверно
(с вероятностью 100%)
находится в известном нам
состоянии
• это стало возможным
благодаря какому-либо каналу
передачи данных от системы к
наблюдателю пропускной
способностью не менее x бит
Кибернетические системы
© Н.М. Светлов, 2006-2011
6/11

7. 2. Понятие «Кибернетическая система»

Система управления, или кибернетическая
система, характеризуется:
целью управления
Управля объектом управления (управляемой
подсистемой)
ющее
воздей факторами неопределённости
ствие
Процесс управления можно представить как процесс снятия
энтропии управляемой подсистемы воздействием со стороны
управляющей подсистемы
Примеры:
холодильник
компьютер
животное
фирма
рынок
Управляемая
подсистема
Управляющая
подсистема
Система управления
Кибернетические системы
© Н.М. Светлов, 2006-2011
7/11

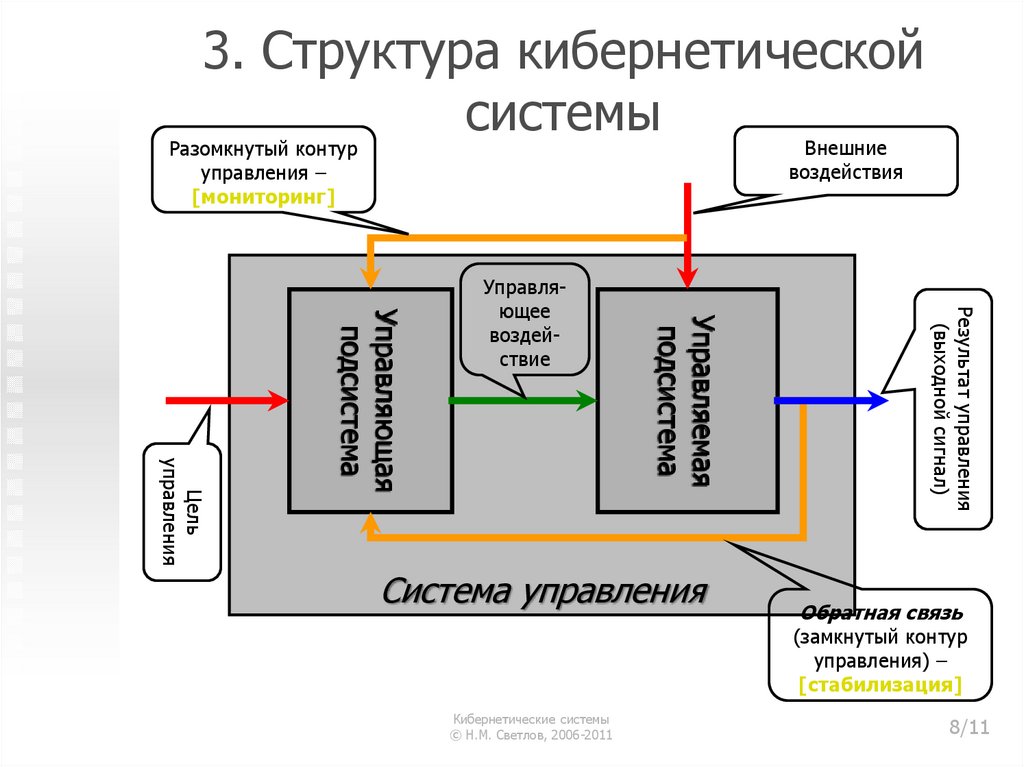
8. 3. Структура кибернетической системы

Внешние
воздействия
Разомкнутый контур
управления –
[мониторинг]
Система управления
Результат управления
(выходной сигнал)
Управляемая
подсистема
Цель
управления
Управляющая
подсистема
Управляющее
воздействие
Обратная связь
(замкнутый контур
управления) –
[стабилизация]
Кибернетические системы
© Н.М. Светлов, 2006-2011
8/11

9. 4. Закон необходимого разнообразия

Энтропия управляемой подсистемы может быть
снята полностью лишь в том случае, если
энтропия управляющей подсистемы не меньше
энтропии управляемой подсистемы
• У. Эшби
Менее сложная система не может полностью
контролировать более сложную
Кибернетические системы
© Н.М. Светлов, 2006-2011
9/11

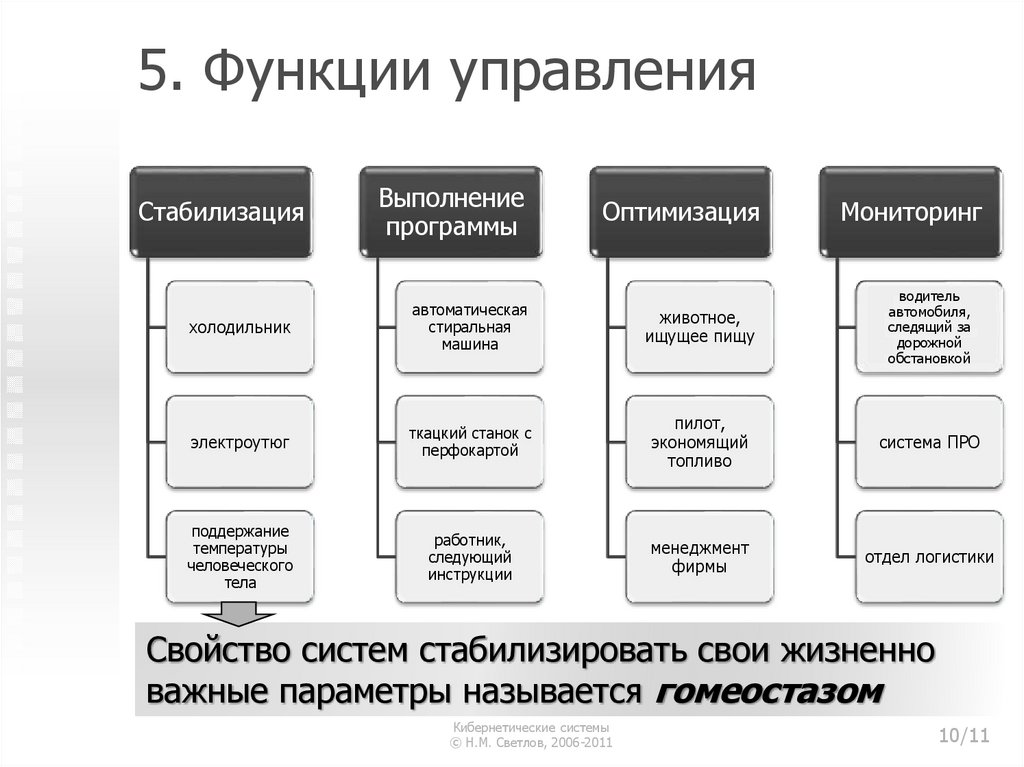
10. 5. Функции управления

Стабилизация
Выполнение
программы
Оптимизация
Мониторинг
холодильник
автоматическая
стиральная
машина
животное,
ищущее пищу
водитель
автомобиля,
следящий за
дорожной
обстановкой
электроутюг
ткацкий станок с
перфокартой
пилот,
экономящий
топливо
система ПРО
поддержание
температуры
человеческого
тела
работник,
следующий
инструкции
менеджмент
фирмы
отдел логистики
Свойство систем стабилизировать свои жизненно
важные параметры называется гомеостазом
Кибернетические системы
© Н.М. Светлов, 2006-2011
10/11

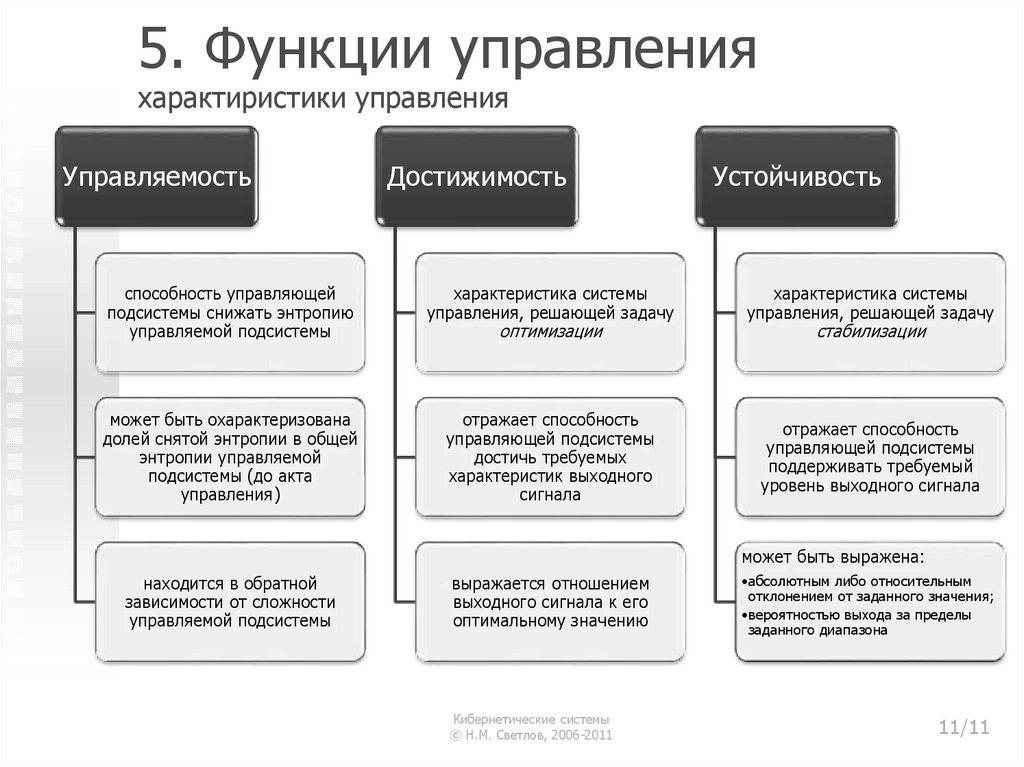
11. 5. Функции управления характиристики управления

Управляемость
Достижимость
Устойчивость
способность управляющей
подсистемы снижать энтропию
управляемой подсистемы
характеристика системы
управления, решающей задачу
характеристика системы
управления, решающей задачу
может быть охарактеризована
долей снятой энтропии в общей
энтропии управляемой
подсистемы (до акта
управления)
отражает способность
управляющей подсистемы
достичь требуемых
характеристик выходного
сигнала
отражает способность
управляющей подсистемы
поддерживать требуемый
уровень выходного сигнала
оптимизации
стабилизации
может быть выражена:
находится в обратной
зависимости от сложности
управляемой подсистемы
выражается отношением
выходного сигнала к его
оптимальному значению
Кибернетические системы
© Н.М. Светлов, 2006-2011
•абсолютным либо относительным
отклонением от заданного значения;
•вероятностью выхода за пределы
заданного диапазона
11/11