Линейная алгебра. Экономические приложения

1. Линейная алгебра

Лекция 7
Экономические приложения

2. Межотраслевой баланс

Межотраслевой баланс (МОБ) — экономико-математическая
балансовая
модель,
характеризующая
межотраслевые
производственные взаимосвязи в экономике страны между
выпуском продукции в одной отрасли и затратами продукции
всех участвующих отраслей, необходимыми для обеспечения
этого выпуска.
2

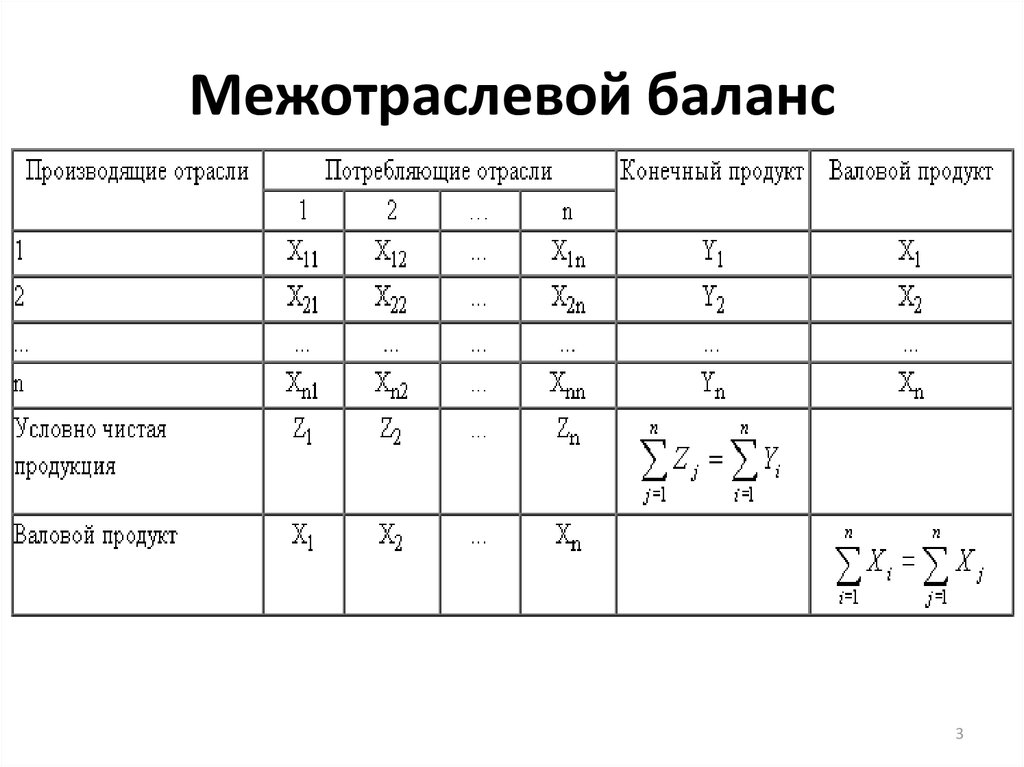
3. Межотраслевой баланс

3

4.

Столбцы отражают состав валового выпуска отраслей
экономики по элементам промежуточного
потребления и добавленной стоимости.
Строки - направления использования ресурсов
каждой отрасли.
4

5. Применения МОБ

Основные задачи применения МОБ:
1.
Определить
объем
производственного
валового
сектора
продукта
экономики
по
известному конечному спросу.
2.
Распределить
по
отраслям
производства
промежуточный продукт каждой отрасли.
5

6. Пример составления модели

Предположения модели:
1.
Некоторый экономический регион производит n видов
продуктов (только своими силами и только для населения
данного региона).
2.
Технологический процесс отработан, а спрос населения на
эти товары изучен.
Требуется определить годовой объем выпуска
продуктов для обеспечения конечного и
производственного потребления.
6

7. Введем обозначения

для известных величин:
yi - спрос населения на i-й продукт (i=1,...,n);
aij - количество i-го продукта, необходимое для выпуска единицы
j-го продукта по данной технологии ( i=1,...,n ; j=1,...,n);
для неизвестных величин:
xi - объем выпуска i-го продукта (i=1,...,n).
7

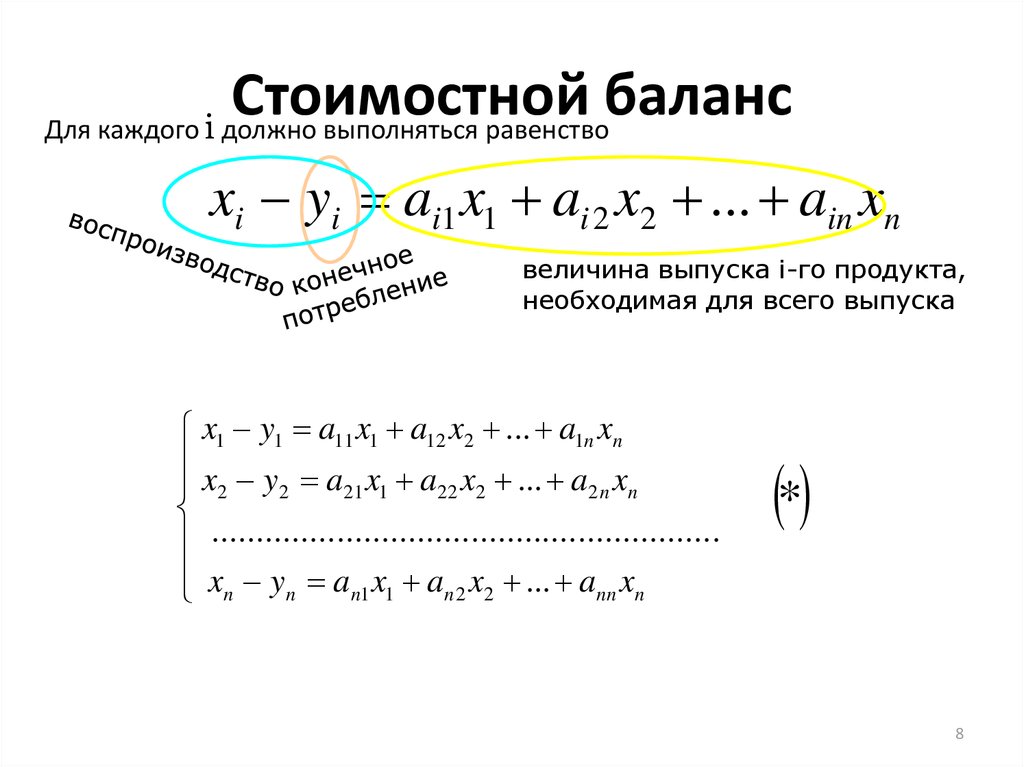
8. Стоимостной баланс

Для каждого i должно выполняться равенство
xi yi ai1 x1 ai 2 x2 ... ain xn
величина выпуска i-го продукта,
необходимая для всего выпуска
x1 y1 a11 x1 a12 x2 ... a1n xn
x y a x a x ... a x
2
2
21 1
22 2
2n n
.........................................................
xn yn an1 x1 an 2 x2 ... ann xn
*
8

9. Модель Леонтьева

Определим
технологическую матрицу
(матрицу прямых затрат)
вектор спроса
y1
y2
Y
y
n
a11
a21
A
...
a
n1
a
a
12
22
...
a
n2
и вектор выпуска
X AX Y , или X AX Y
a
a
...
2n
,
... ...
... ann
...
1n
x1
x2
X .
x
n
- классическая модель
«затраты-выпуск».
9

10. Формулировки модели Леонтьева

Эквивалентные формулировки уравнения
межотраслевого баланса:
AX Y X
- каноническая форма
X ( E A) 1 Y
Матрица
- приведенная форма
(E – A)-1 называется матрицей полных затрат.
10

11. Задачи

Типовые задачи, возникающие при изучении
межотраслевого баланса:
ЗАДАЧА 1. Найти матрицу
А
- прямых затрат.
ЗАДАЧА 2. Дана матрица
А
прямых затрат и
вектор
X
валового выпуска. Найти вектор
конечного продукта
Y.
Решение:
Y = (E-A)X
11

12. Задачи

ЗАДАЧА 3 (основная).
Дана матрица
А
прямых затрат и вектор
конечного продукта. Найти вектор
Y
X валового выпуска.
Решение:
1-й способ - решение СЛУ
2-й способ - нахождение
(Е-А)X=Y
X=(Е-А)-1Y
12

13. Продуктивность матрицы прямых затрат модели Леонтьева

Определение.
Матрица прямых затрат модели Леонтьева (все элементы
неотрицательны) называется продуктивной, если для
любого неотрицательного вектора конечного выпуска Y
найдётся неотрицательный вектор валового выпуска X с
данной матрицей прямых затрат.
В этом случае и модель Леонтьева называется
продуктивной.
13

14. Теорема (первый критерий продуктивности)

Модель Леонтьева с неотрицательной матрицей А
продуктивна тогда и только тогда, когда
существует неотрицательная матрица (Е–А)-1.
14

15. Теорема (второй критерий продуктивности)

Матрица А с неотрицательными элементами продуктивна, если
сумма элементов по любому ее столбцу (строке) не превосходит
единицы:
a
n
i 1
ij
1
Причем хотя бы для одного столбца (строки) эта сумма строго
меньше единицы.
15

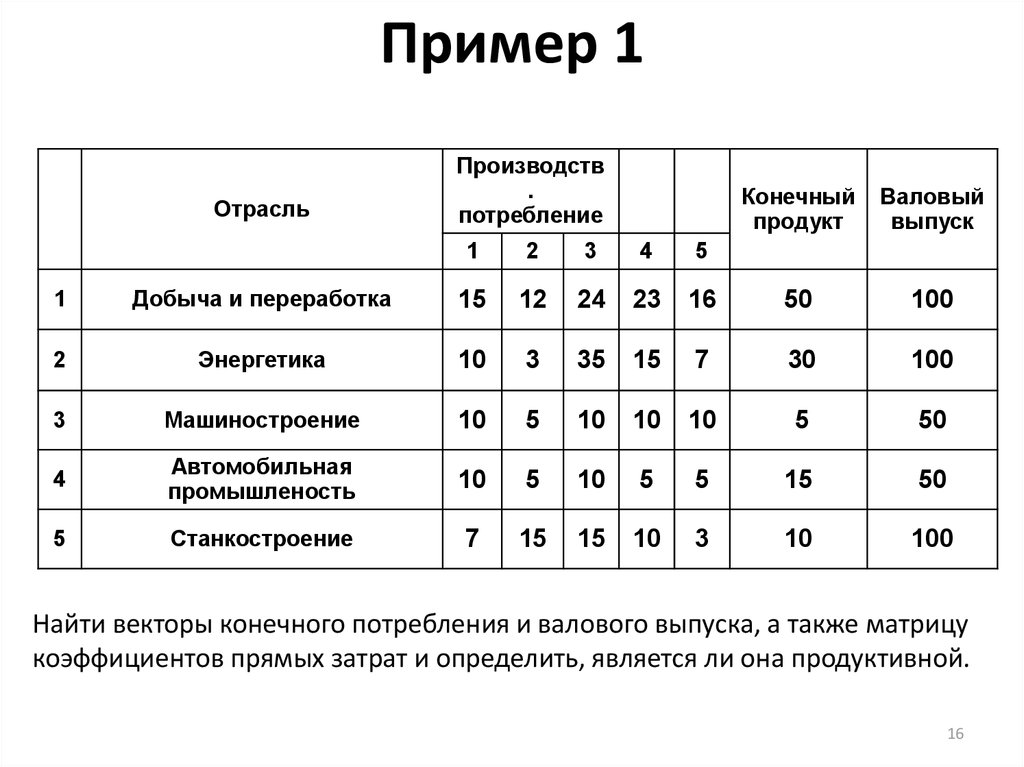
16. Пример 1

В таблице приведены данные по балансу:
Отрасль
Производств
.
потребление
1
2
3
4
5
Конечный
продукт
Валовый
выпуск
1
Добыча и переработка
15
12
24
23
16
50
100
2
Энергетика
10
3
35
15
7
30
100
3
Машиностроение
10
5
10
10
10
5
50
4
Автомобильная
промышленость
10
5
10
5
5
15
50
5
Станкостроение
7
15
15
10
3
10
100
Найти векторы конечного потребления и валового выпуска, а также матрицу
коэффициентов прямых затрат и определить, является ли она продуктивной.
16

17. Пример 1 (продолжение)

100
50
100
30
X 50 , Y 5 ,
50
15
100
10
0,15
0,10
A 0,10
0,10
0,07
xij aij x j , i, j 1,2,..., n
0,12
0,48
0,46
0,03
0,70
0,30
0,05
0,20
0,20
0,05
0,20
0,10
0,15
0,30
0,20
0,16
0,07
0,10
0,05
0,03
17

18. Пример 1 (продолжение)

Все элементы матрицы А положительны. Сумма элементов
третьего и четвертого столбцов больше единицы.
Следовательно, условия второго критерия продуктивности не
соблюдены, матрица А не является продуктивной.
Экономическая причина: внутреннее потребление
отраслей 3 и 4 слишком велико в соотношении с их
валовыми выпусками.
18

19. Пример 2

Дан баланс трех отраслей промышленности за некоторый
период времени:
Отрасль
Производств.
потребление
1
2
3
Конечный
продукт
Валовый
выпуск
1
Тяжелая
промышленность
5
35
20
40
100
2
Легкая
промышленность
10
10
20
60
100
3
Сельское
хозяйство
20
10
10
10
50
1. Построить матрицу полных затрат.
2. Найти объем валового выпуска каждого вида продукции, если
конечное потребление по отраслям увеличить соответственно на 60,
70, 30 усл.ед.
19

20. Пример 2 (продолжение)

100
40
X 100 , Y 60 ,
50
10
0,05 0,35 0,40
A 0,10 0,10 0,40
0,20 0,10 0,20
Матрица А удовлетворяет обоим критериям продуктивности. В
случае заданного увеличения конечного потребления новый
60
вектор конечного продукта Y* будет иметь вид
Y * 70
30
Новый вектор валового выпуска X* найдем из
X * AX * Y * , или
E A X * Y *
20

21. Пример 2 (продолжение)

1 0 0 0,05
E A 0 1 0 0,10
0 0 1 0,20
Решаем систему
0,35
0,10
0,10
0,40 0,95 0,35 0,40
0,40 0,10
0,90 0,40
0,20 0,20 0,10
0,80
E A X * Y *
, получаем
152,6
X * 135,8
92,5
Таким образом, для заданного увеличения компонент вектора конечного
продукта, необходимо увеличить соответствующие валовые выпуски:
тяжелой промышленности на 52,2%, легкой промышленности — на 35,8% и
сельского хозяйства — на 85%.
21

22. Пример 3

Дано уравнение межотраслевого баланса для двух
отраслей:
2
xi xij yi , i 1, 2
i 1
500 100 160 240
400 275 40 85
Требуется определить, каким должен быть вектор
валового выпуска, чтобы конечный продукт 1-й
отрасли увеличился вдвое, а 2-й – на 20%.
22

23. Пример 3 (продолжение)

Решение:
100
A 500
275
500
Пример 3 (продолжение)
160
0 .2
400
40 0.55
400
0 .4
.
0 .1
480
1 0 .2 0 .4
; E A
;
Y0
102
0.55 1 0.1
1
0.8 0.4 480
X 0 ( E A) Y0
0.9 102
0.55
1.8 0.8 480 945.6
X 0
1.1 1.6 102 691.2
1
23

24. Пример 3 (продолжение)

Даны матрица
продукта
Y
А
прямых затрат и вектор конечного
:
A
1
3
1
2
1
6
1
4
,
Найти вектор валового выпуска
Решение:
1
Y .
3
X.
X E A Y ,
1
2
X 3
1
2
1
6
3
4
1
1 9 10 1 39
3 6 8 3 30
24

25. Модель международной торговли

Пусть x1, x2, … , xn – бюджеты торгующих стран,
a11
a21
A
...
a
n1
a
a
12
22
...
a
n2
a
a
– структурная матрица торговли,
...
2n
... ...
... ann
...
1n
xij - часть бюджета i-й страны, которую она тратит на
торговлю с j-й страной. Тогда выручка i-й страны составит
pi a x1 ai 2 x2 ... ain xn
i1
25

26. Модель международной торговли

Какими должны быть соотношения между
бюджетами торгующих между собой стран,
чтобы торговля была взаимовыгодной?
p1 a11 x1 a12 x2 ... a1n xn x1
p2 a21 x1 a22 x2 ... a2 n xn x2
pn an1 x1 an 2 x2 ... ann xn xn
26

27. Замечание о модели международной торговли

Модель международной торговли является частным
случаем модели МОБ.
Роль отраслей играют государства.
Все товары, которые государство производит идут в
потребление либо в своей стране, либо в странахпартнерах (все товары рассматриваются как конечные).
27

28. Теорема (условие бездефицитности торговли)

Пусть
А
– структурная матрица торговли,
– вектор бюджетов торгующих стран.
Тогда условием бездефицитной торговли
является следующее равенство:
X
А.X=X ,
т.е. вектор
X
должен быть собственным
А , отвечающим
собственному числу 1.
вектором матрицы
28