Похожие презентации:
Кинематика вращательного движения
1. Омский государственный технический университет Кафедра физики
Калистратова Л.Ф.Электронные лекции по разделам классической и
релятивистской механики
6 лекций
(12 аудиторных часов)
2. Тема 2. Кинематика вращательного движения
Тема лекции2.1. Угловое перемещение. Угловая скорость.
2.2. Угловое ускорение.
2.3. Обратная задача кинематики при вращательном
движении.
2.4. Взаимосвязь линейных и угловых величин.
3. 2.1. Угловое перемещение. Угловая скорость.
Любое движение абсолютно твёрдого тела может бытьсведено к сумме двух движений – поступательного
и вращательного.
При вращательном движении различные точки
твёрдого тела движутся по-разному.
Вращательное движение нельзя охарактеризовать
движением определённой точки.
4.
При вращательном движении все точки теладвижутся по окружностям, центры которых
лежат на одной неподвижной прямой,
называемой осью вращения.
При вращательном движении радиус-векторы,
проведённые из центров соответствующих
окружностей к точкам тела за время dt
поворачиваются на один и тот же угол d .
5.
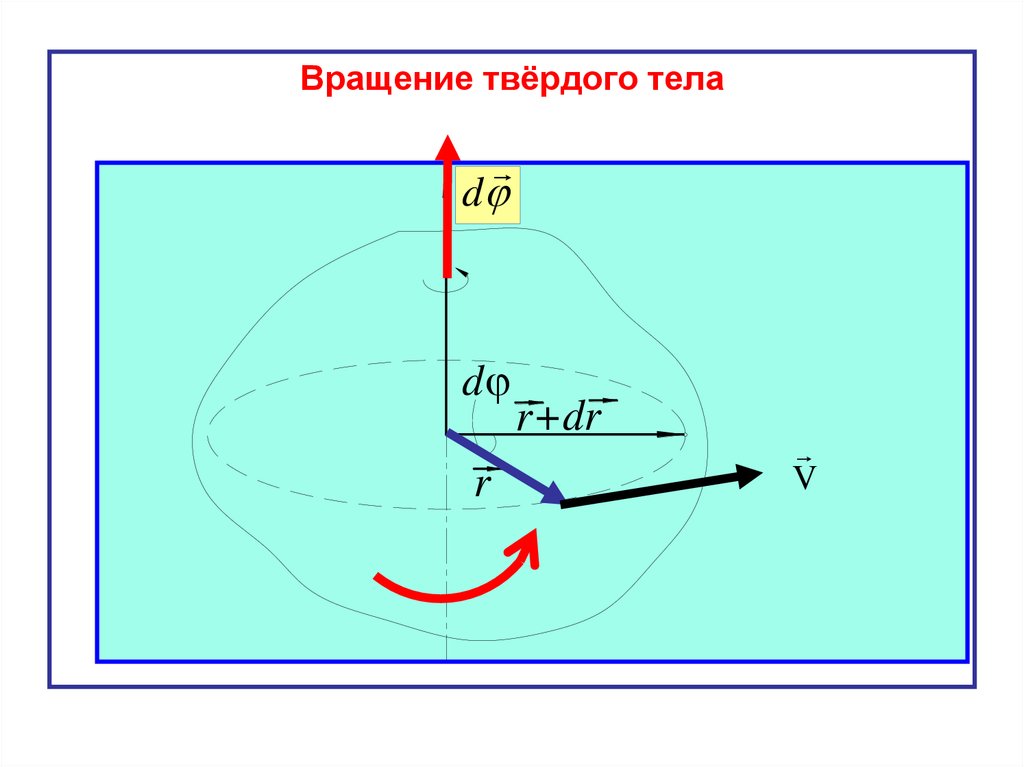
Вращение твёрдого телаd
d
r
r+dr
V
6.
Угловое перемещение d– вектор, численно
равный углу поворота d радиус-вектора
определённой точки вращающегося тела.
- измеряется в радианах: [φ] = рад.
Его направление определяется правилом буравчика:
Вектор d направлен вдоль оси вращения так, что
если смотреть с его конца, то вращение тела
должно происходить против часовой
стрелки.
d d
d
7.
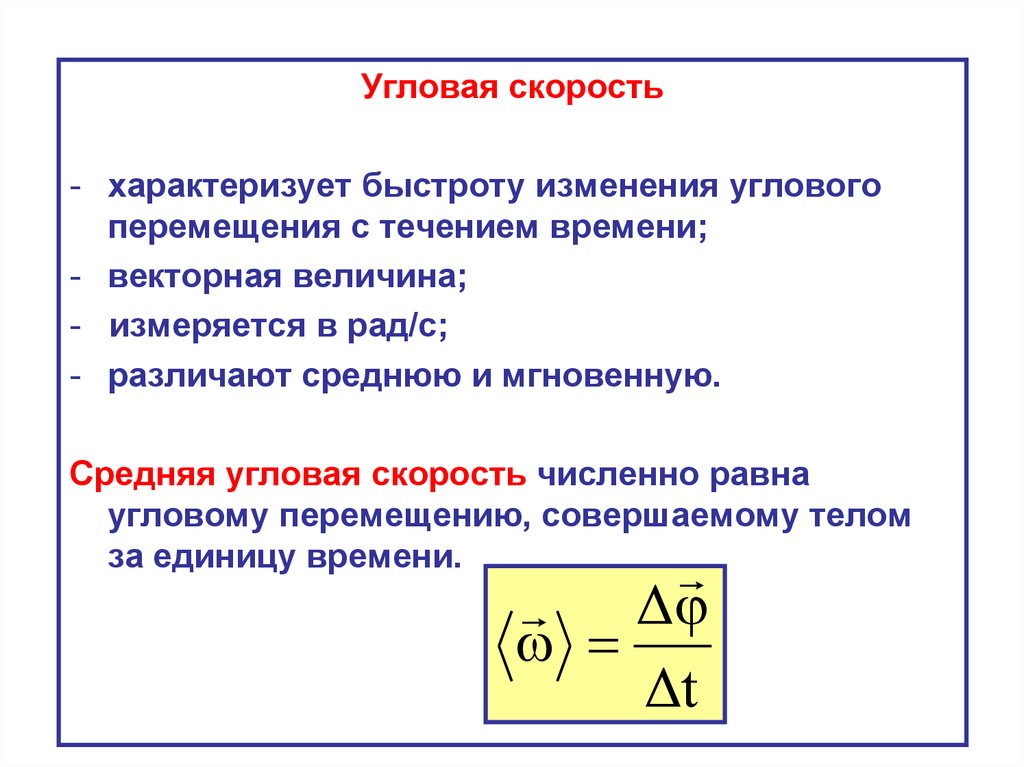
Угловая скорость- характеризует быстроту изменения углового
перемещения с течением времени;
- векторная величина;
- измеряется в рад/с;
- различают среднюю и мгновенную.
Средняя угловая скорость численно равна
угловому перемещению, совершаемому телом
за единицу времени.
Δ
Δt
8.
Мгновенная угловая скорость равна пределу, ккоторому стремится средняя угловая скорость
при неограниченном убывании промежутка
времени до нуля.
Δ
d
ω lim
Δt 0 Δt
dt
Мгновенная угловая скорость равна первой
производной от углового перемещения по
времени.
d
dt
ω
d
ω
dt
Вектор угловой скорости
направлен по оси
вращения и определяется по правилу буравчика.
9.
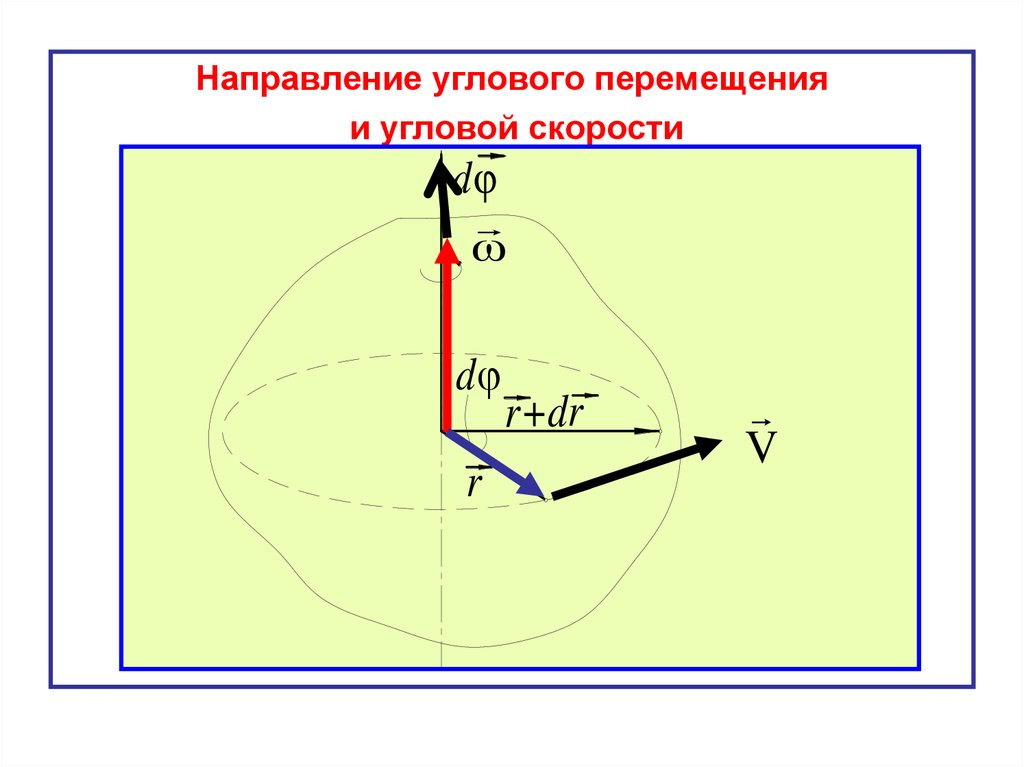
Направление углового перемещенияи угловой скорости
d
ω
d
r
r+dr
V
10.
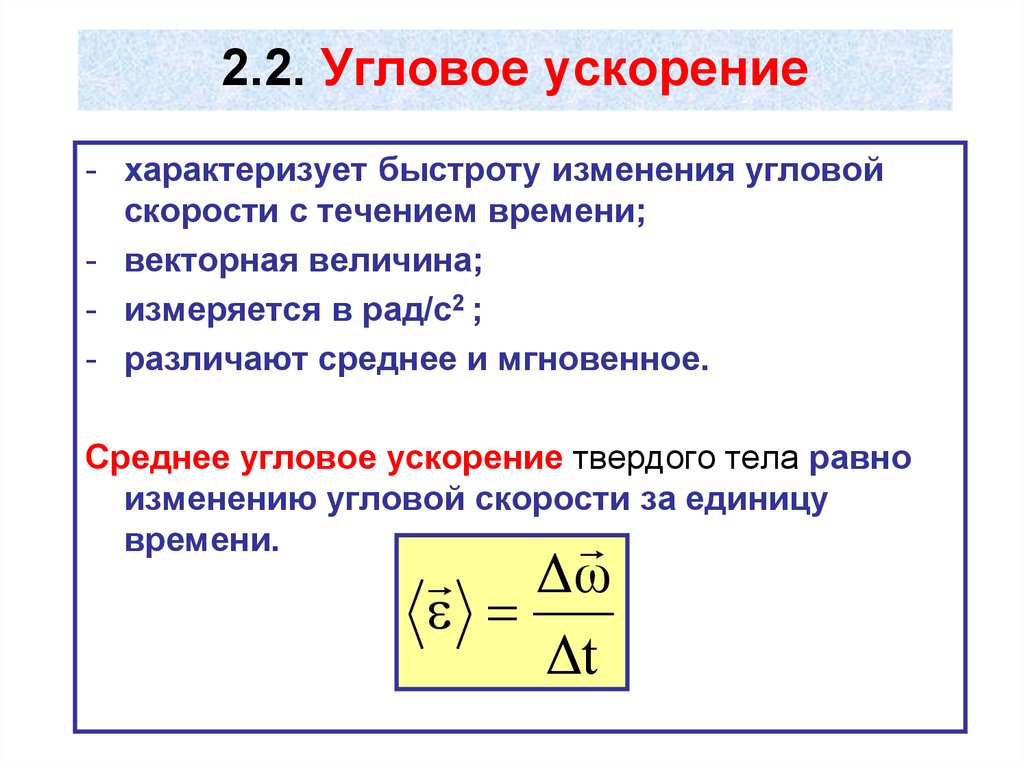
2.2. Угловое ускорение- характеризует быстроту изменения угловой
скорости с течением времени;
- векторная величина;
- измеряется в рад/с2 ;
- различают среднее и мгновенное.
Среднее угловое ускорение твердого тела равно
изменению угловой скорости за единицу
времени.
Δω
Δt
11.
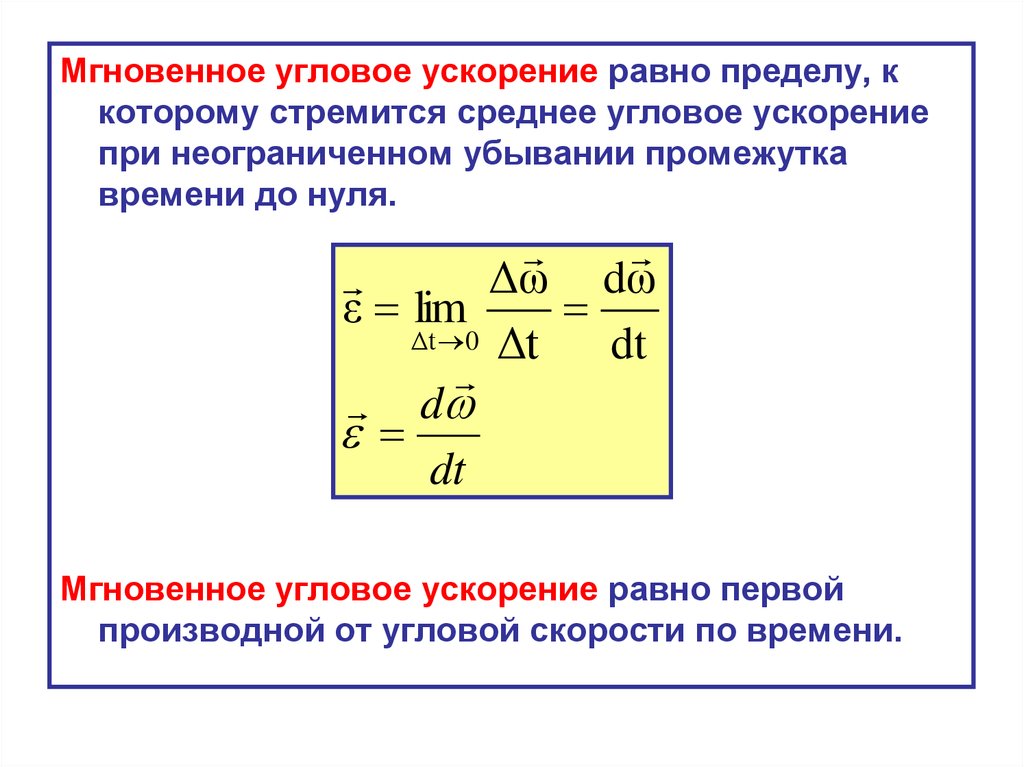
Мгновенное угловое ускорение равно пределу, ккоторому стремится среднее угловое ускорение
при неограниченном убывании промежутка
времени до нуля.
Δω dω
ε lim
Δt 0 Δt
dt
d
dt
Мгновенное угловое ускорение равно первой
производной от угловой скорости по времени.
12.
Модуль мгновенного углового ускорения равенпервой производной от модудя угловой
скорости по времени или второй производной
от углового перемещения по времени.
d
ε
dt
2
d
2
dt
13.
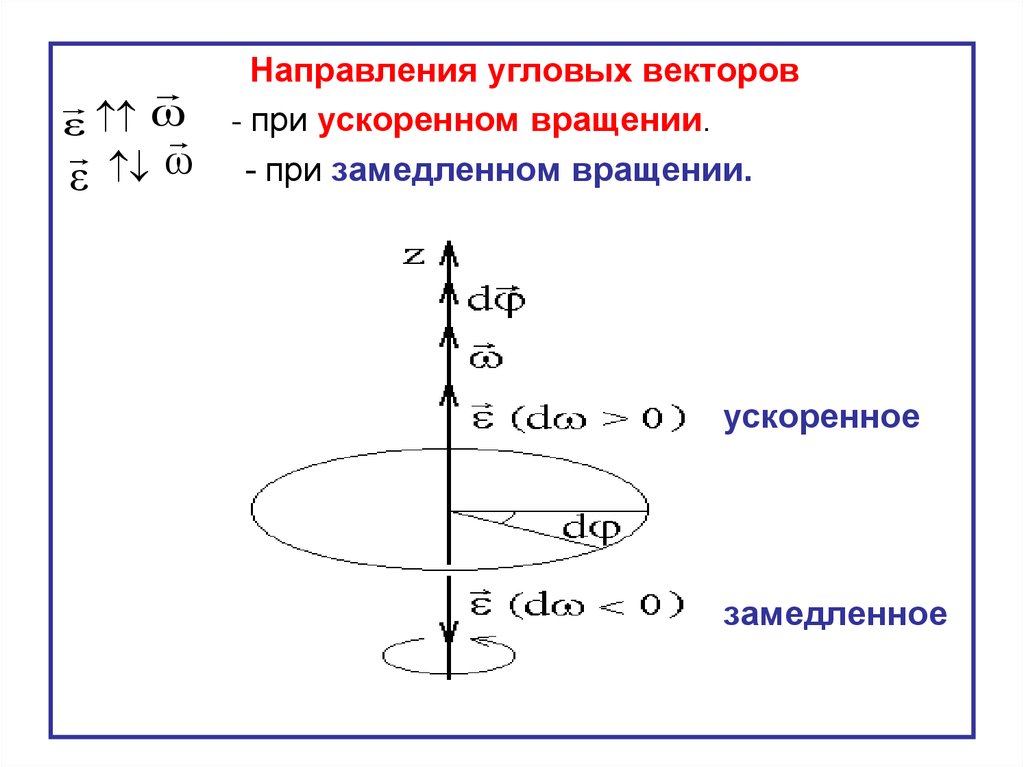
Направления угловых векторовε ω - при ускоренном вращении.
ω - при замедленном вращении.
ε
ускоренное
замедленное
14.
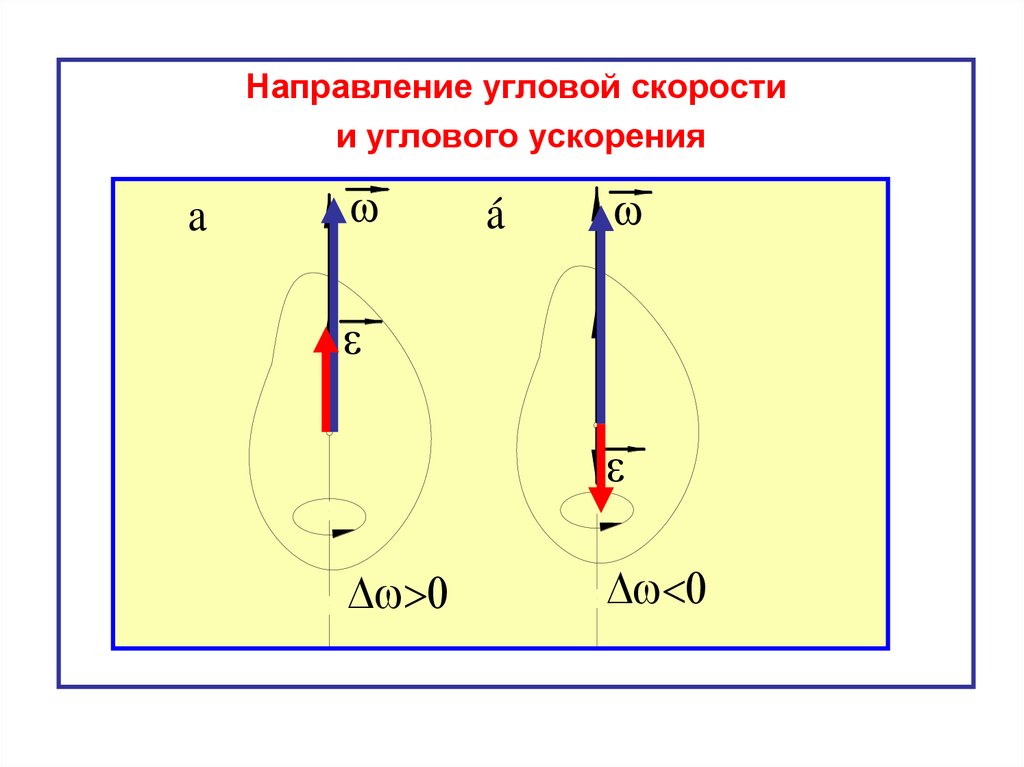
Направление угловой скоростии углового ускорения
á
a
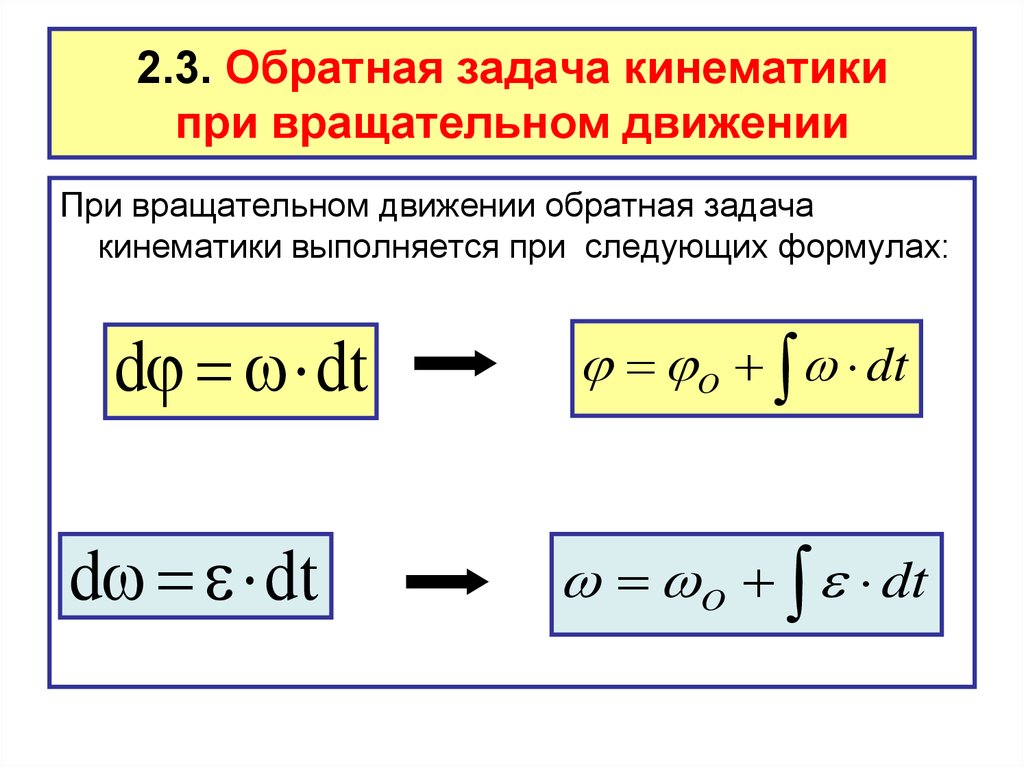
15. 2.3. Обратная задача кинематики при вращательном движении
При вращательном движении обратная задачакинематики выполняется при следующих формулах:
d dt
d dt
O dt
O dt
16.
= 0,= t.
При равномерном вращении
= const,
При равнопеременном вращении
0 t
εt
ω0 t
2
2
= const
17.
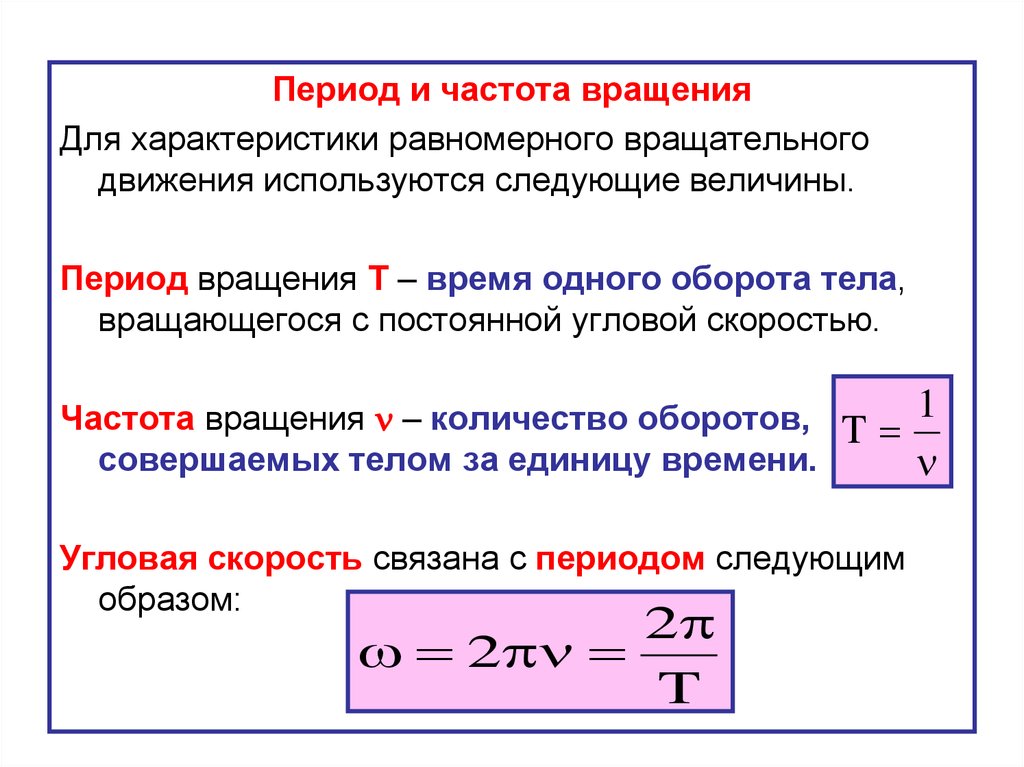
Период и частота вращенияДля характеристики равномерного вращательного
движения используются следующие величины.
Период вращения Т – время одного оборота тела,
вращающегося с постоянной угловой скоростью.
Частота вращения – количество оборотов, T 1
совершаемых телом за единицу времени.
Угловая скорость связана с периодом следующим
образом:
2
2
T
18. 1.4. Взаимосвязь угловых и линейных величин
Кроме угловых величин: углового перемещения,угловой скорости и углового ускорения движение
каждой точки вращающегося твердого тела
характеризуют линейные величины:
линейное перемещение dr ,
линейный путь dS,
линейная скорость v ,
тангенциальное ускорение a τ
,
нормальное ускорение a n ,
полное ускорение a .
19.
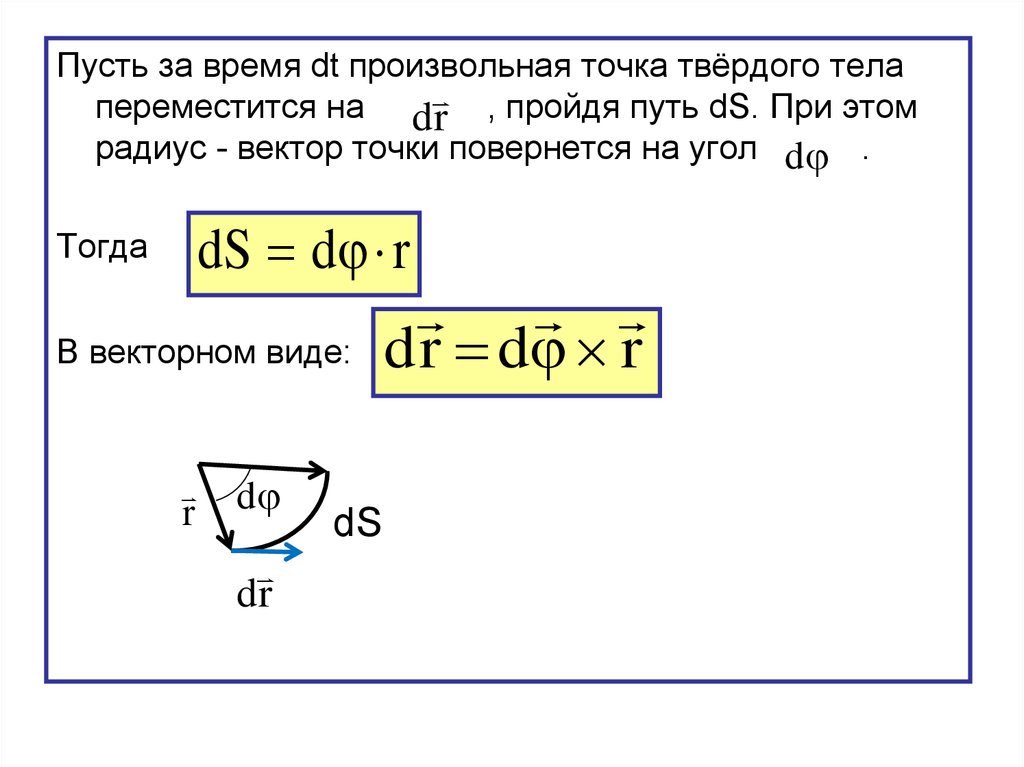
Пусть за время dt произвольная точка твёрдого телапереместится на d r , пройдя путь dS. При этом
радиус - вектор точки повернется на угол d .
Тогда
dS d r
В векторном виде:
d
r
dr
dS
d r d r
20.
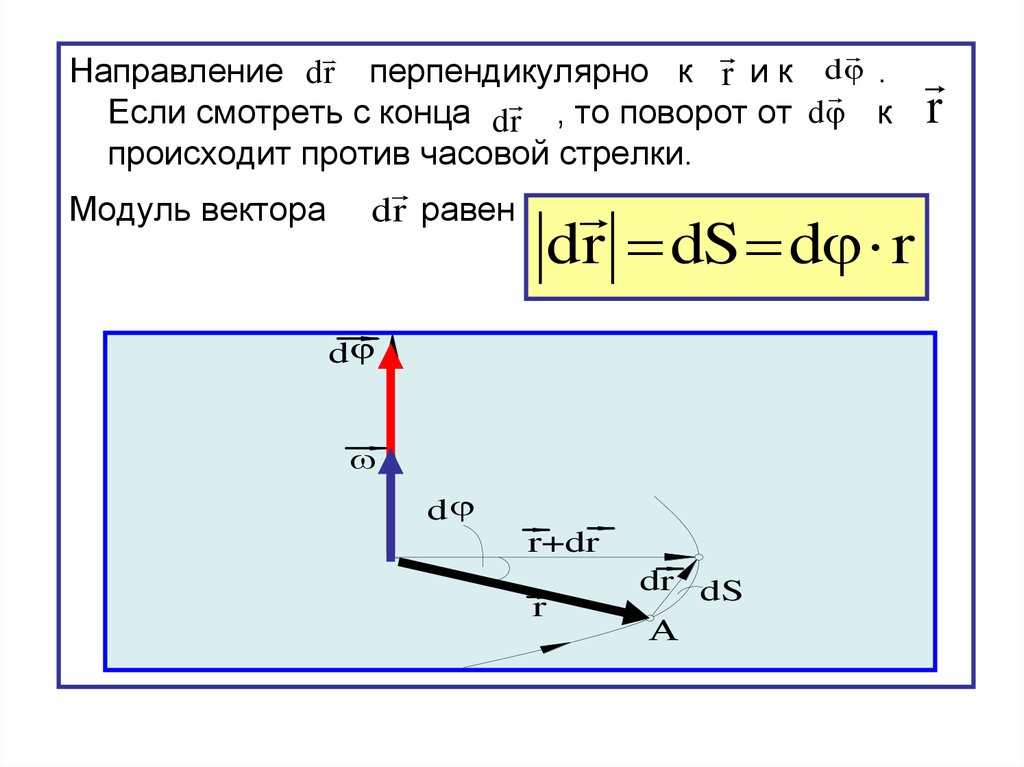
Направление dr перпендикулярно к r и к d .Если смотреть с конца dr , то поворот от d к
происходит против часовой стрелки.
Модуль вектора dr равен
dr dS d r
d
d
r+dr
r
dr dS
r
21.
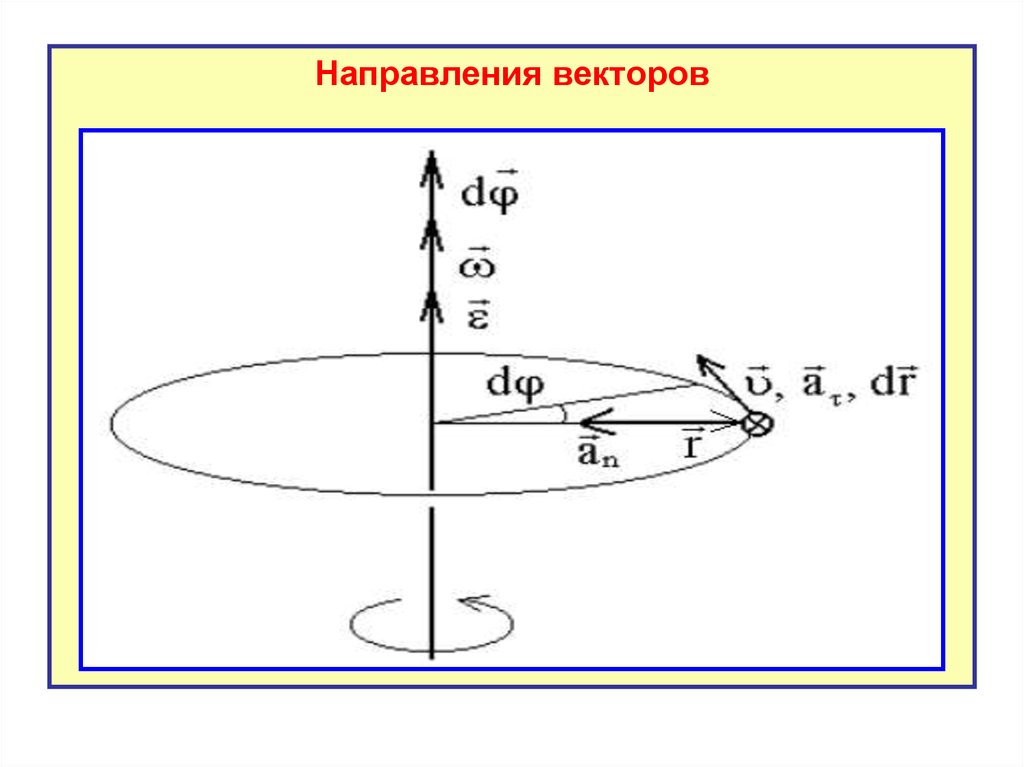
Направления векторов22.
Вектор элементарного перемещения:d r d
r
dt dt
Разделим это соотношение на dt:
Учтём, что
Получим
dr
V
dt
d r d r
d
ω
dt
v r
.
Линейная скорость данной точки твёрдого тела равна
векторному произведению угловой скорости на
радиус - вектор точки.
23.
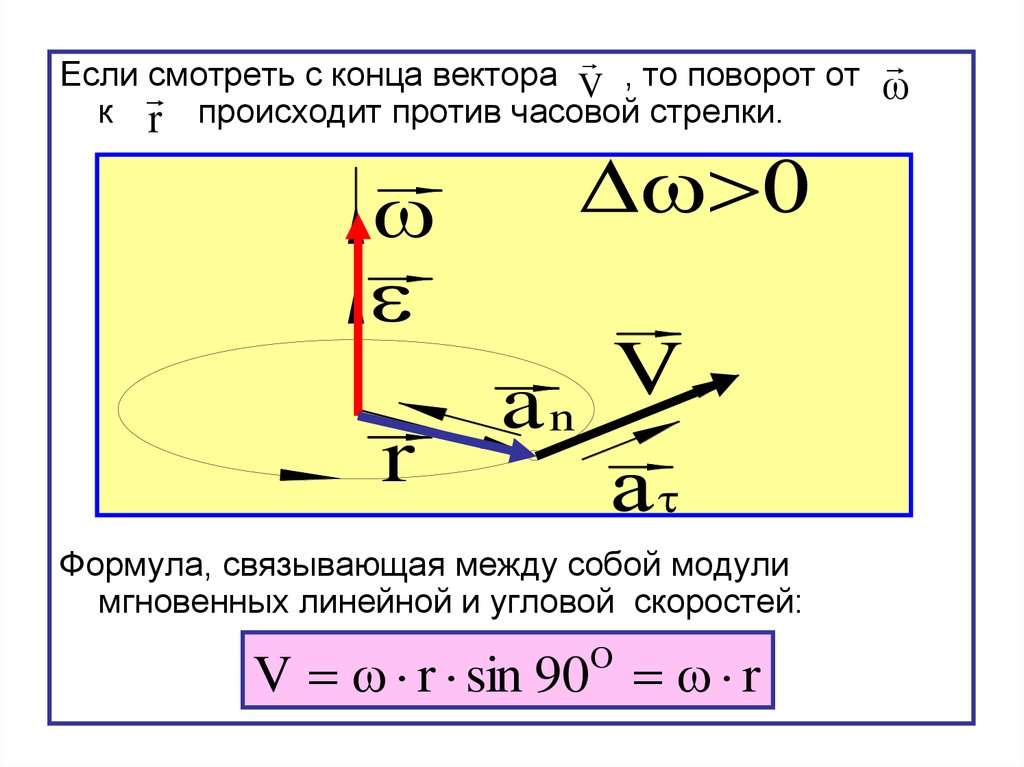
Если смотреть с конца вектора V , то поворот от ωк r происходит против часовой стрелки.
r
V
an
Формула, связывающая между собой модули
мгновенных линейной и угловой скоростей:
V r sin 90 r
O
24.
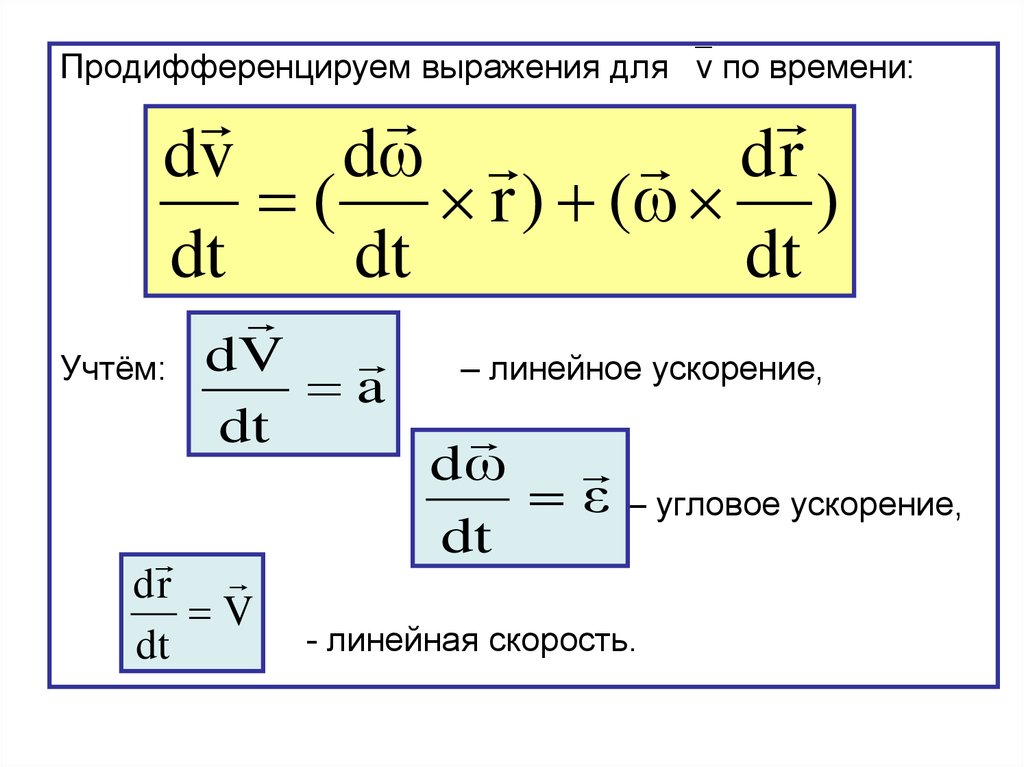
Продифференцируем выражения для v по времени:dr
dv
d
( r ) ( )
dt
dt
dt
Учтём:
dV
a
dt
dr
V
dt
– линейное ускорение,
dω
ε
dt
– угловое ускорение,
- линейная скорость.
25.
a ( r ) ( v )a aτ an
Получим
и сравним
Первый вектор в правой части - тангенциальное
ускорение.
Второй вектор – нормальное ускорение.
26.
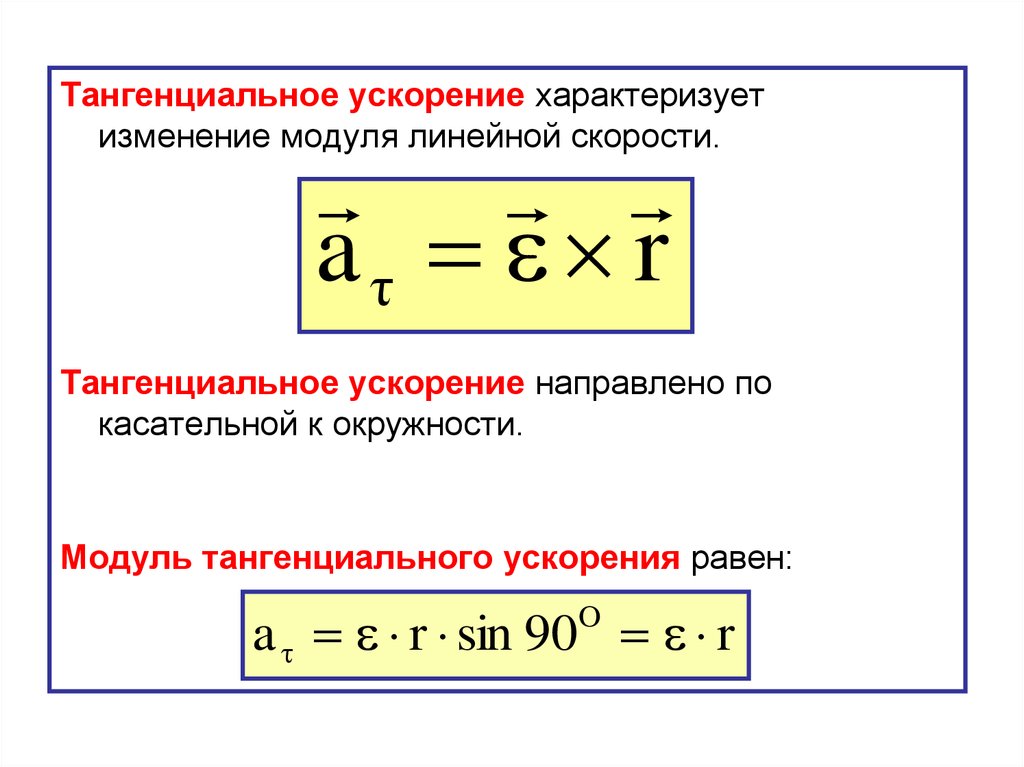
Тангенциальное ускорение характеризуетизменение модуля линейной скорости.
aτ r
Тангенциальное ускорение направлено по
касательной к окружности.
Модуль тангенциального ускорения равен:
a r sin 90 r
O
27.
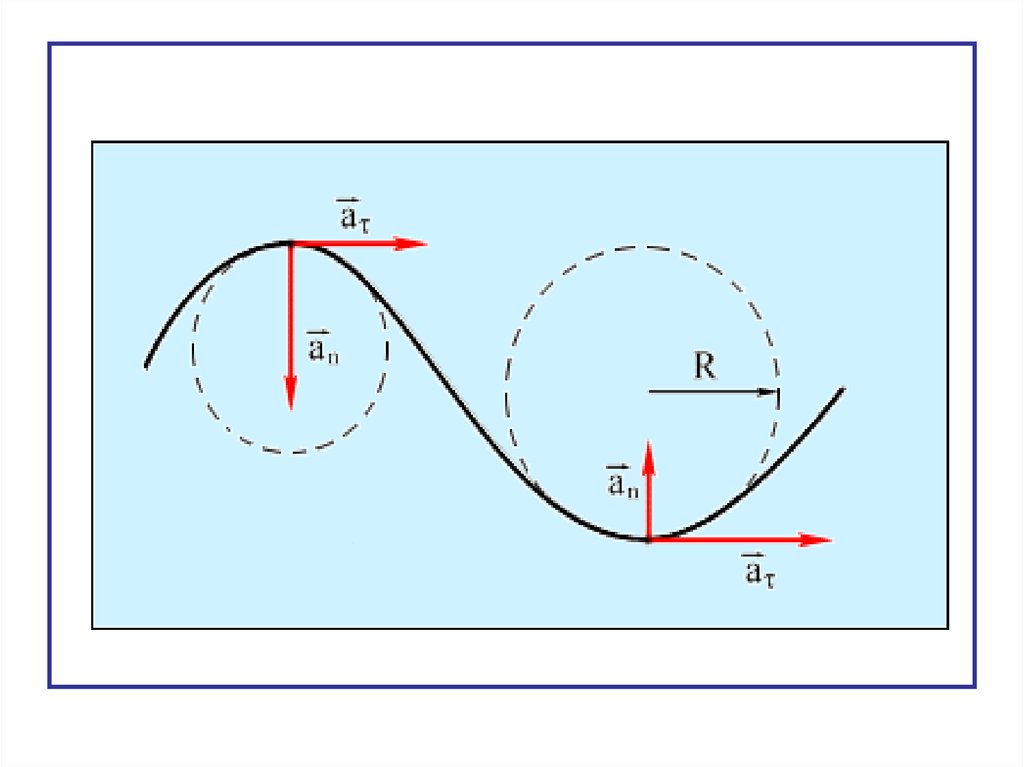
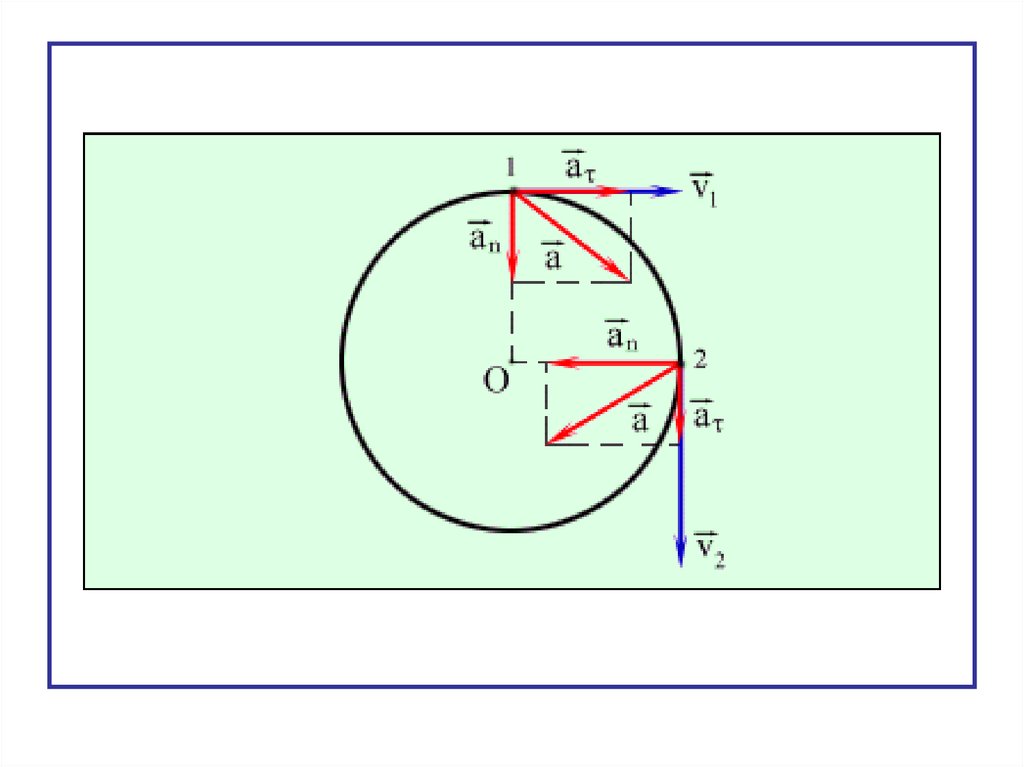
Нормальное ускорение характеризует изменениенаправления линейной скорости.
a n v
a ε, r ω, v
a ω, v
Нормальное ускорение направлено к центру
n
окружности.
Модуль нормального ускорения равен
V
a n V sin 90 V r
r
O
2
2












 Физика
Физика








