Похожие презентации:
Кинематика вращательного движения абсолютно твердого тела
1.
Кинематика вращательного движенияабсолютно твердого тела
Абсолютно твердое тело – это система
материальных точек, расстояния между
которыми не меняются в процессе движения.
Основными видами движения твердого
тела являются:
•поступательное,
•простое вращательное (вращение вокруг
неподвижной оси).
1
2.
Поступательное движение – это движение,при котором все точки твердого тела
совершают за один и тот же промежуток
времени одинаковые перемещения.
Задача
описания
поступательного
движения твердого тела сводится к задаче
кинематики материальной точки.
Простое
вращательное
движение
(вращение вокруг неподвижной оси) – это
движение, при котором все точки твердого
тела движутся по окружностям, центры
которых лежат на оси вращения.
2
3.
Кинематика вращательного движенияабсолютно твердого тела
1.Угловое перемещение.
2. Угловая скорость.
3. Угловое ускорение.
4. Законы равноускоренного
вращательного движения.
5. Связь линейных и угловых
характеристик движения.
4.
1.Угловое перемещение dВектор d называется
d
R
d
R
вектором углового перемещения
• он численно равен углу поворота радиусвектора материальной точки за время dt
• направление его определяется по правилу
правого винта.
Единицей измерения углового перемещения в
СИ является радиан (рад).
Угол поворота радиус- вектора является
функцией времени: φ = φ(t)
5.
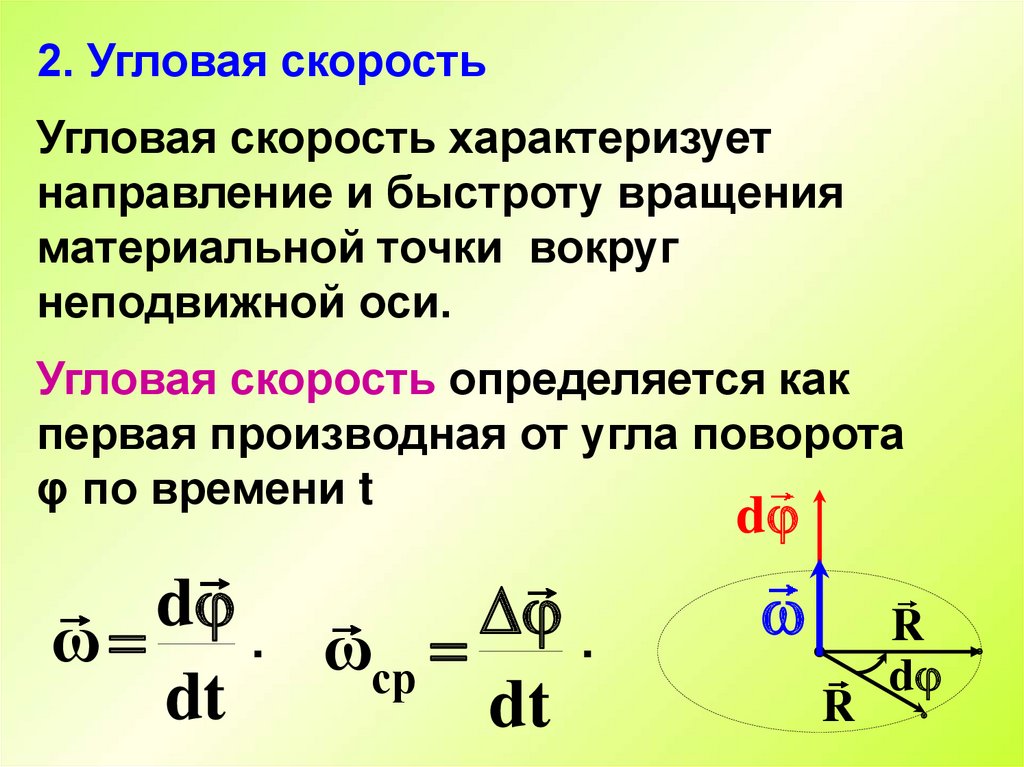
2. Угловая скоростьУгловая скорость характеризует
направление и быстроту вращения
материальной точки вокруг
неподвижной оси.
Угловая скорость определяется как
первая производная от угла поворота
φ по времени t
d
d .
.
ω
ωср
dt
dt
R
d
R
6.
3. Угловое ускорениеБыстроту изменения угловой скорости
характеризует вектор углового
ускорения:
d
dt
В СИ угловое ускорение измеряется в
радианах на секунду в квадрате (рад/с2).
ср
- среднее ускорение.
dt
7.
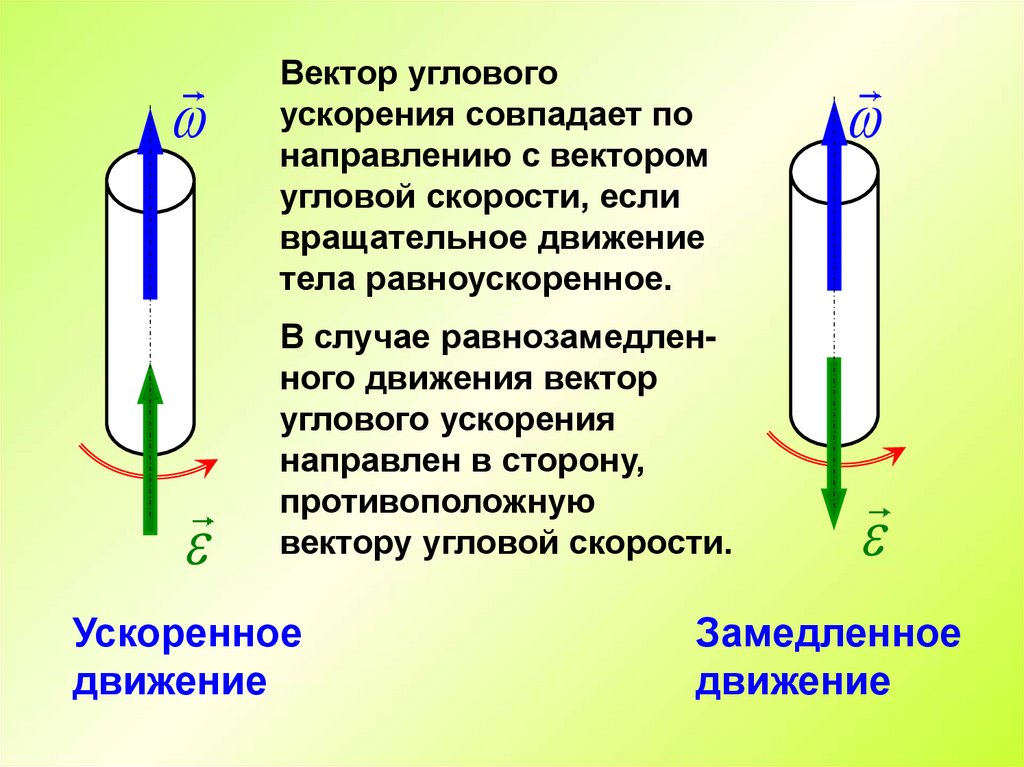
Вектор угловогоускорения совпадает по
направлению с вектором
угловой скорости, если
вращательное движение
тела равноускоренное.
В случае равнозамедленного движения вектор
углового ускорения
направлен в сторону,
противоположную
вектору угловой скорости.
Ускоренное
движение
Замедленное
движение
8.
4. Законы равноускоренноговращательного движения
Равноускоренным называется вращение
с постоянным угловым ускорением
ω0
ω0
ω ω0 t
ω ω0 t
t
ω0 t
2
2
t
ω0 t
2
2
9.
5. Связь линейных и угловыххарактеристик движения
Пусть материальная точка движется по
окружности радиуса R, и за время dt
перемещается по дуге окружности
длиной dS.
dS R d
dS R d
dt
dt
dS d R
v R ω
10.
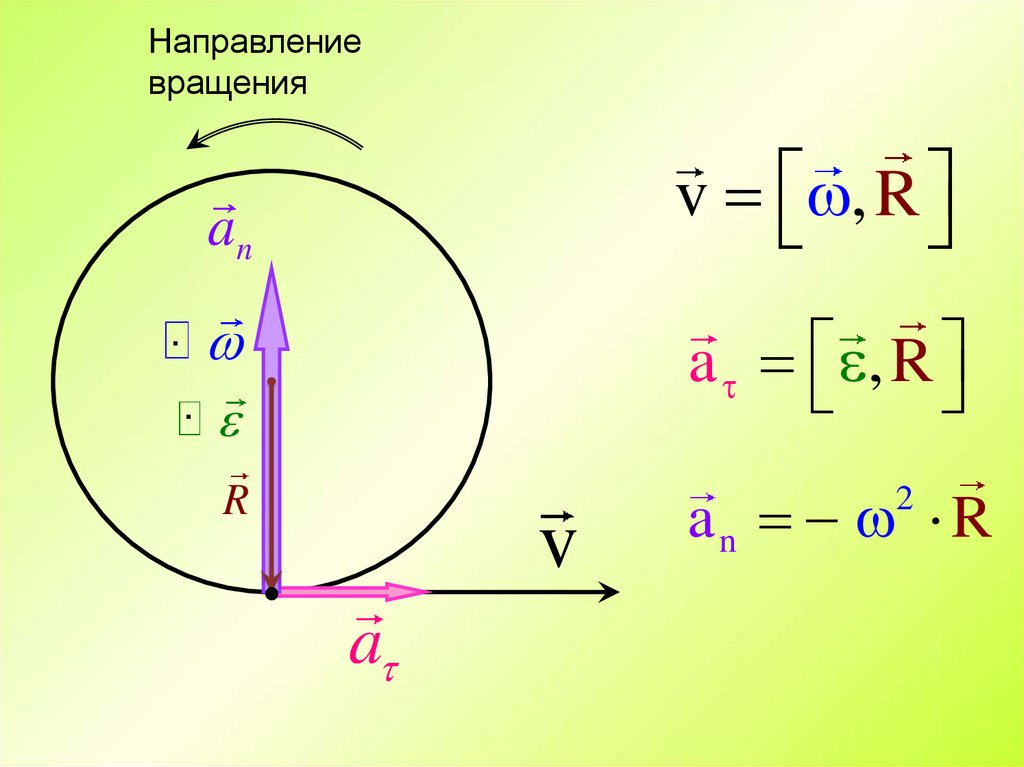
Направлениевращения
v , R
an
∙
∙
a , R
R
v
a
an R
2
11.
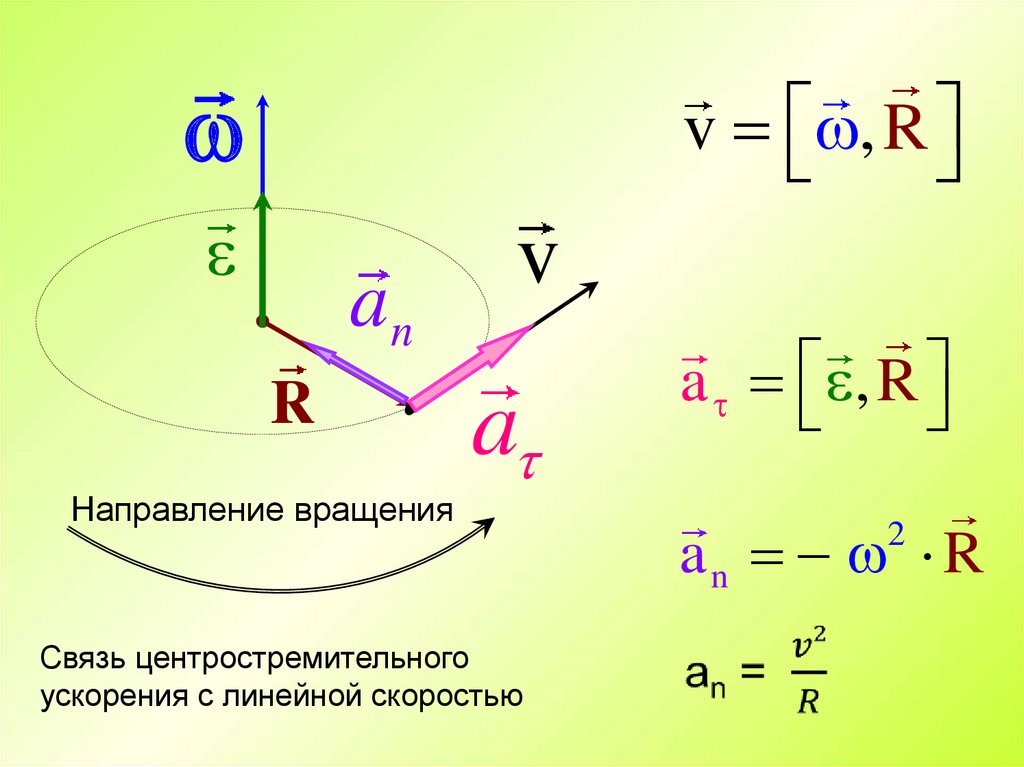
v , Ran
R
Направление вращения
v
a
Связь центростремительного
ускорения с линейной скоростью
a , R
an R
2
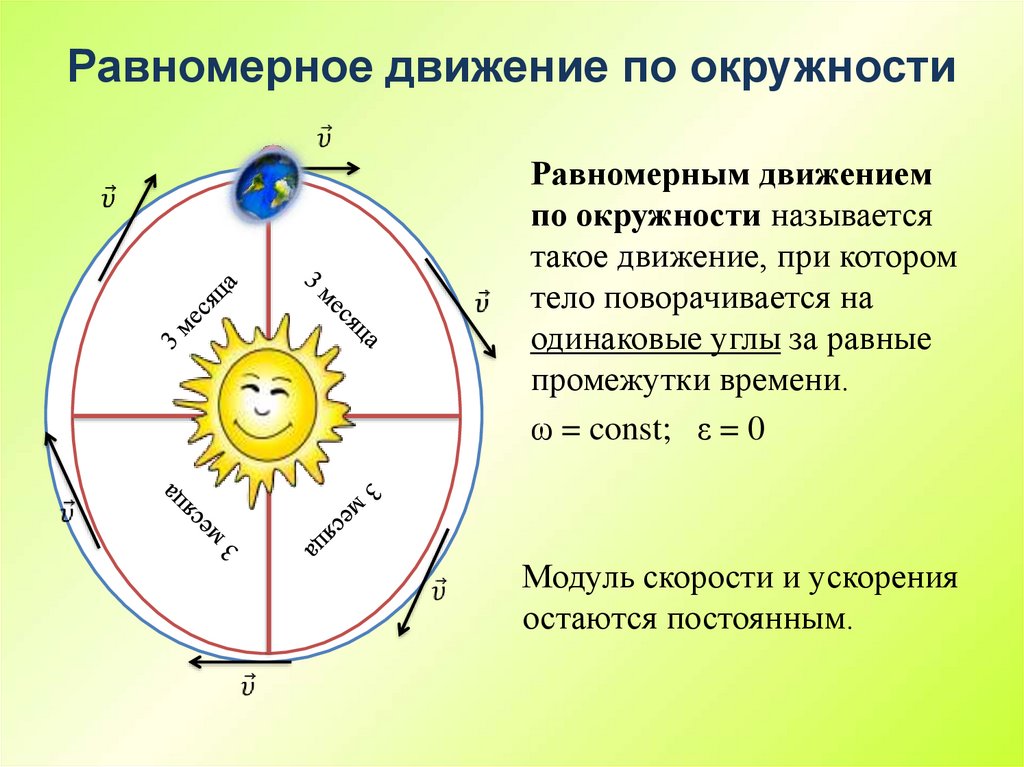
12. Равномерное движение по окружности
Равномерным движениемпо окружности называется
такое движение, при котором
тело поворачивается на
одинаковые углы за равные
промежутки времени.
ω = const; ε = 0
Модуль скорости и ускорения
остаются постоянным.
13. Кинематика вращательного движения материальной точки
Равномерное движение по окружности14. Кинематика вращательного движения материальной точки
Равномерное движение по окружности15.
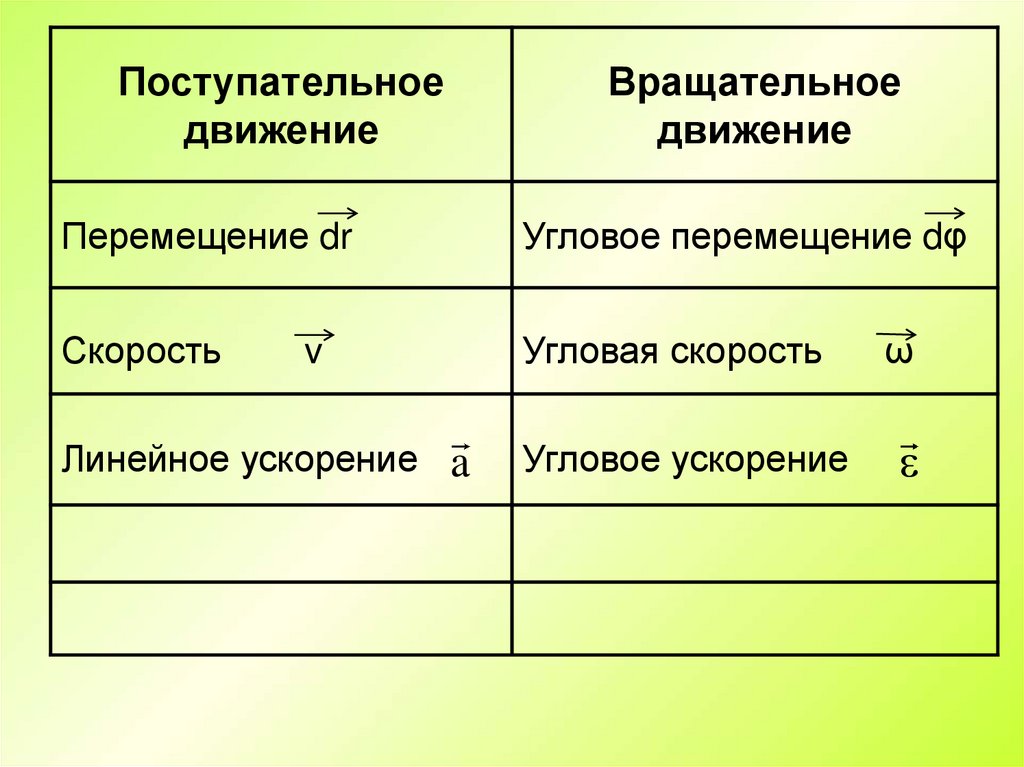
Поступательноедвижение
Вращательное
движение
Перемещение dr
Угловое перемещение dφ
Скорость
Угловая скорость
v
Линейное ускорение
a
Угловое ускорение
ω
16.
Динамика вращательного движенияабсолютно твердого тела
1. Момент силы.
2. Момент инерции. Теорема Штейнера.
3. Основной закон динамики
вращательного движения.
17.
1. Момент силыМоментом силы F относительно неподвижной
точки О называется векторная физическая
величина M, равная векторному
произведению радиус-вектора r,
проведенного из точки О в точку приложения
силы, на силу F .
Вектор момента
силы направлен
перпендикулярно
плоскости,
образованной
векторами r и F .
18.
Модуль вектора момента силы M r F sin .α – угол между векторами r и F.
Введём обозначение r sin d и назовём d
плечом силы F .
Плечо силы – это кратчайшее расстояние от
точки О до линии действия силы.
M r F sin
M F d
r sin d
В СИ момент силы
измеряется в ньютонах
умноженных на метр (Н м).
19.
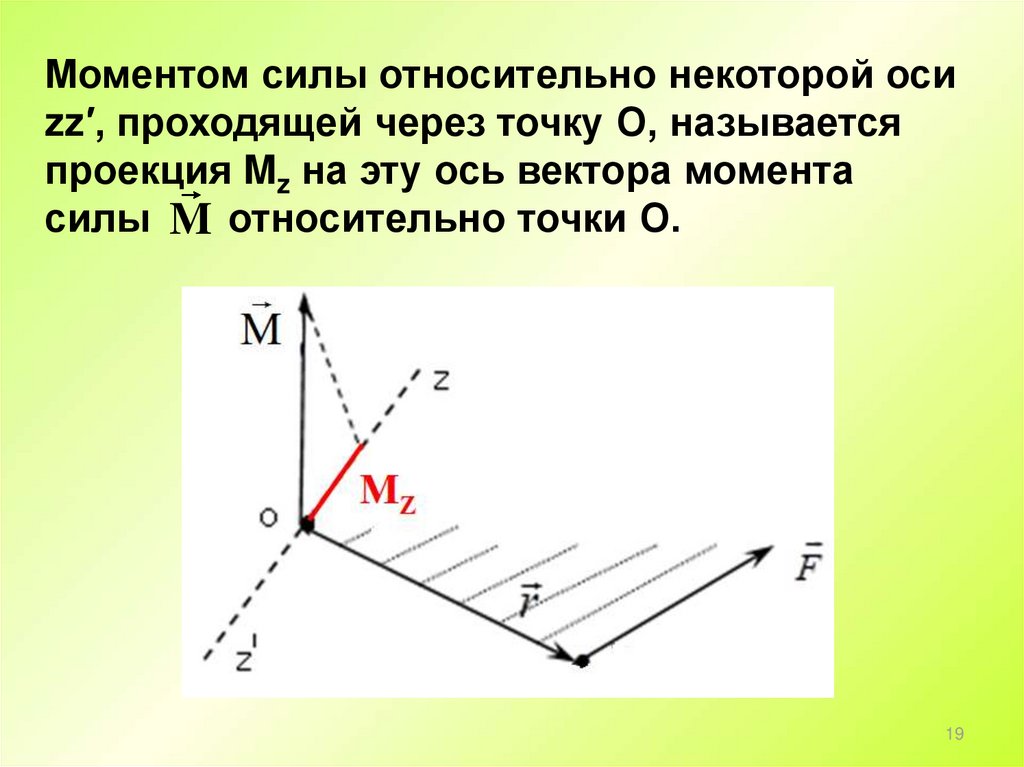
Моментом силы относительно некоторой осиzz′, проходящей через точку О, называется
проекция Mz на эту ось вектора момента
силы M относительно точки О.
19
20.
2. Момент инерции. Теорема ШтейнераИнертность – это свойство материальных тел,
проявляющееся в том, что тело сохраняет
состояние покоя или равномерного движения,
когда внешние воздействия на тело
отсутствуют.
Инертность тела при простом вращательном
движении зависит не только от массы, но и от
ее распределения относительно оси
вращения.
21.
Момент инерции I – физическая величина,количественно характеризующая инертность
твёрдого тела, проявляющуюся во
вращательном движении.
Момент инерции материальной точки
I m r2
m – масса материальной точки;
r – расстояние от материальной точки до оси
вращения.
Момент инерции I – скалярная аддитивная
величина
22.
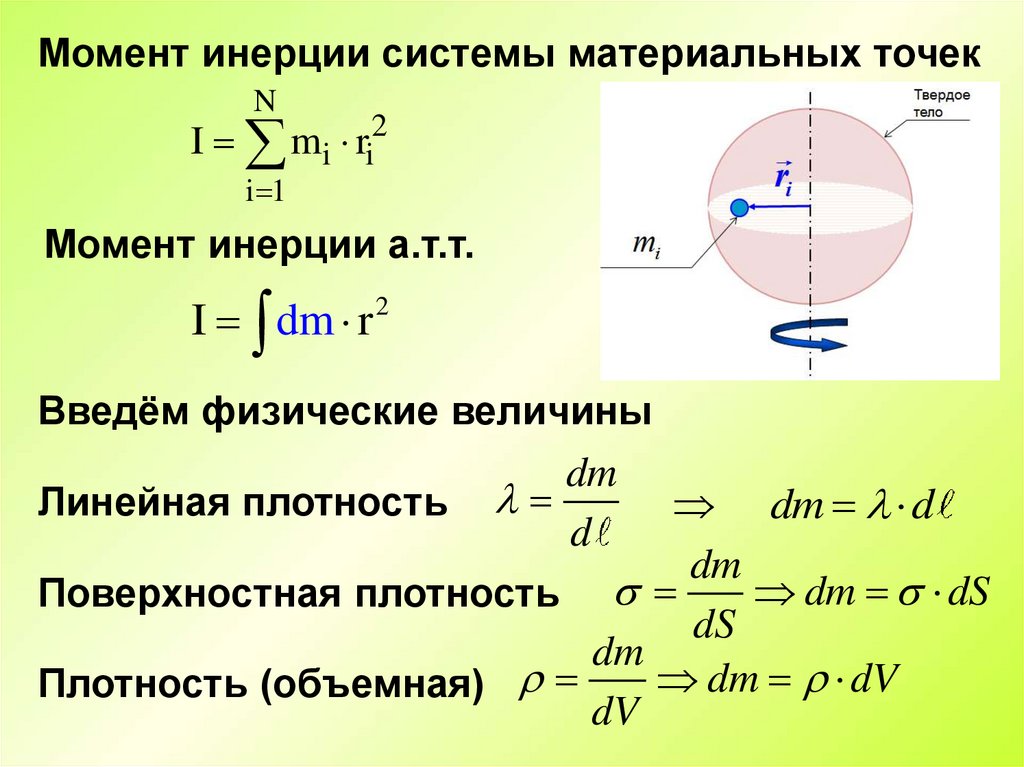
Момент инерции системы материальных точекN
I mi ri2
i 1
Момент инерции а.т.т.
I dm r 2
Введём физические величины
dm
d
dm d
dm
dm dS
Поверхностная плотность
dS
dm
dm dV
Плотность (объемная)
dV
Линейная плотность
23.
Момент инерции стержня относительно осипроходящей через конец стержня
m
I dm r
z
2
dm
dm dr
I dr r
0
r
dr
2
dm
3
r
I dr r
3
0
2
0
3
3
m
m
3
3
3
2
24.
Теорема Штейнера: момент инерции I телаотносительно произвольной оси О′О′ равен
сумме:
• момента инерции IС этого тела
относительно оси ОО, проходящей через
центр масс тела параллельно О′О′, и
• произведения массы m тела на квадрат
расстояния а между осями
a
a
I IС m a
2
25.
Момент инерции стержняотносительно оси
проходящей через центр
масс - IC
z
a
2
С
I Z IС m a 2
IС I Z m a
m
IZ
3
a
2
2
2
m
IС
3
2
m
4
2
1
m
12
2
26.
Момент инерции однородного обручаотносительно оси, проходящей через центр
масс обруча перпендикулярно его плоскости
I C R 2 dm
R
С Z
dm d
d
dm
2 R
m
2 R
IC R
2
2 R
0
IC
R2 d
0
m
R 2 2 R m R 2
d R 2 R
2 R
2
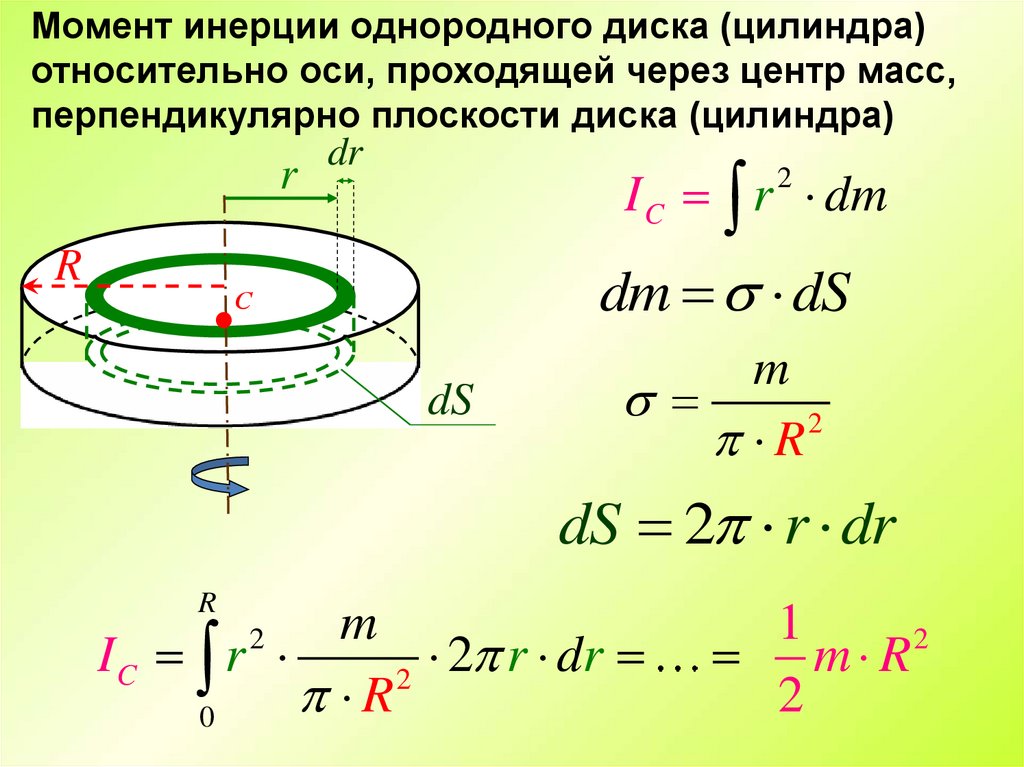
27.
Момент инерции однородного диска (цилиндра)относительно оси, проходящей через центр масс,
перпендикулярно плоскости диска (цилиндра)
r
R
dr
I C r dm
2
dm dS
С
dS
m
R2
dS 2 r dr
R
m
IC r
2 r dr
2
R
0
2
1
2
m R
2
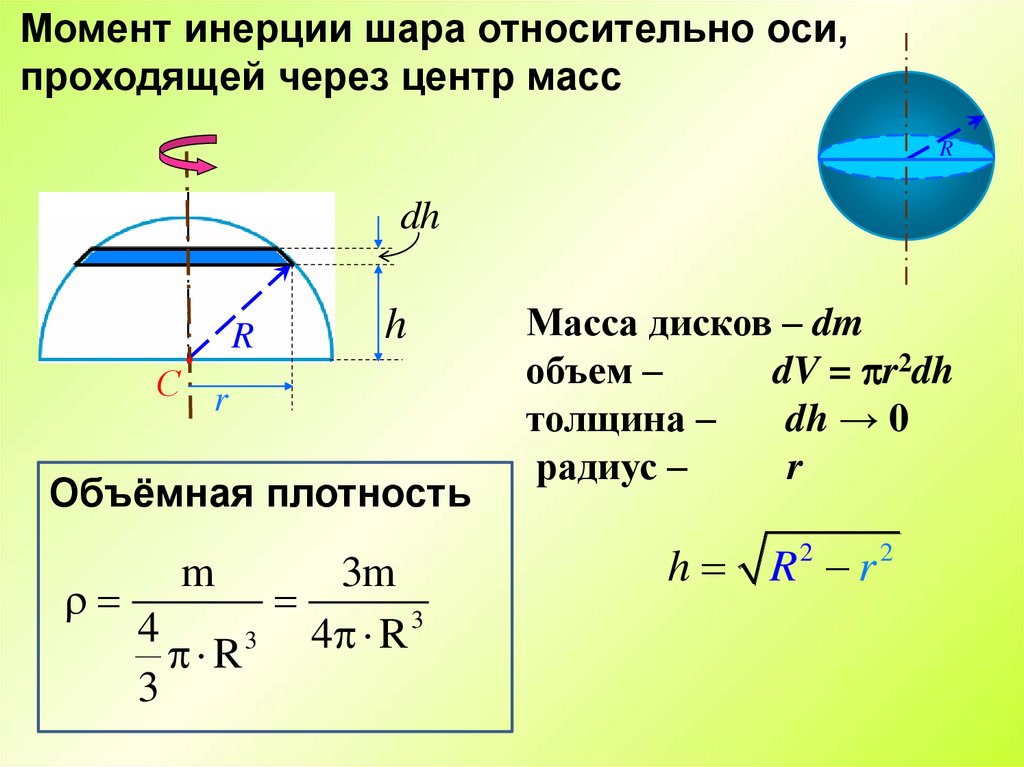
28.
Момент инерции шара относительно оси,проходящей через центр масс
R
dh
R
h
С r
Объёмная плотность
m
3m
3
4
4
R
3
R
3
Масса дисков – dm
объем –
dV = r2dh
толщина –
dh → 0
радиус –
r
h R2 r 2
29.
БЫЛО:h R r
2
dh
2r
2
2
dr 2 R r
2
2
R2 r 2
1 2
dI r dm
2
Моменты инерции дисков:
I1
r
1 2
1 2
1
r dm r dV r 2 r 2 dh
2
2
2
dh
IC 2 I 1
2
2rdr
2 R r
2
R
m
3 R
4
2
3
0
rdr
R2 r 2
r 5 dr
2
mR 2
R2 r 2 5
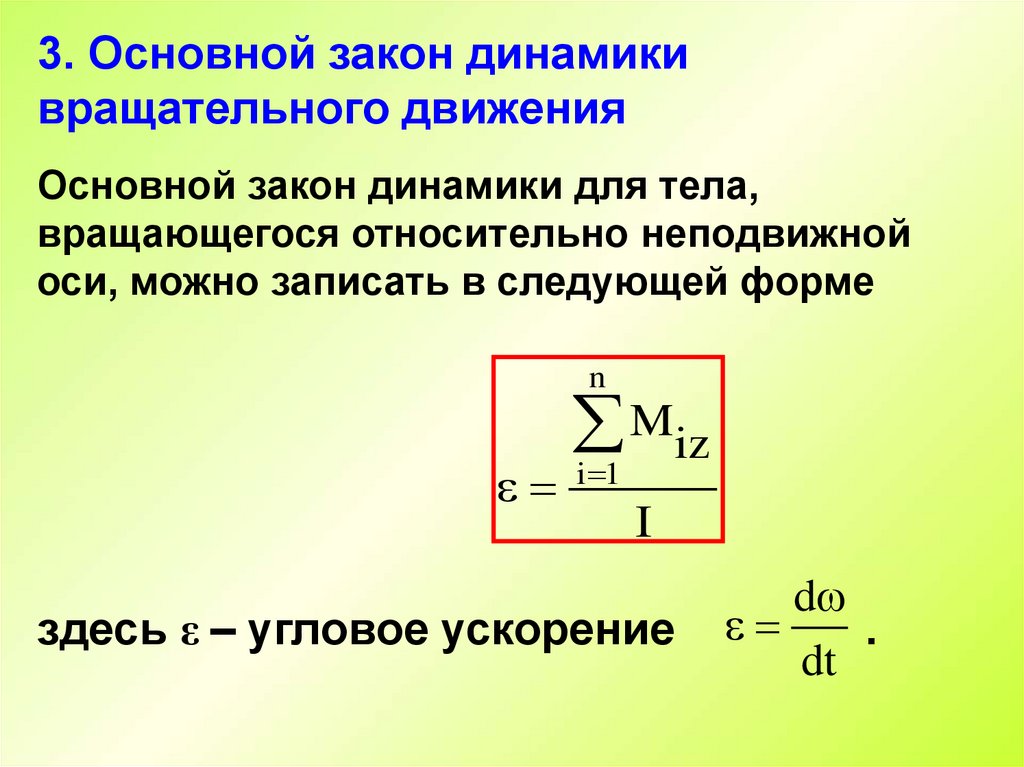
30.
3. Основной закон динамикивращательного движения
Основной закон динамики для тела,
вращающегося относительно неподвижной
оси, можно записать в следующей форме
n
Miz
i 1
I
здесь ε – угловое ускорение
d
.
dt
31.
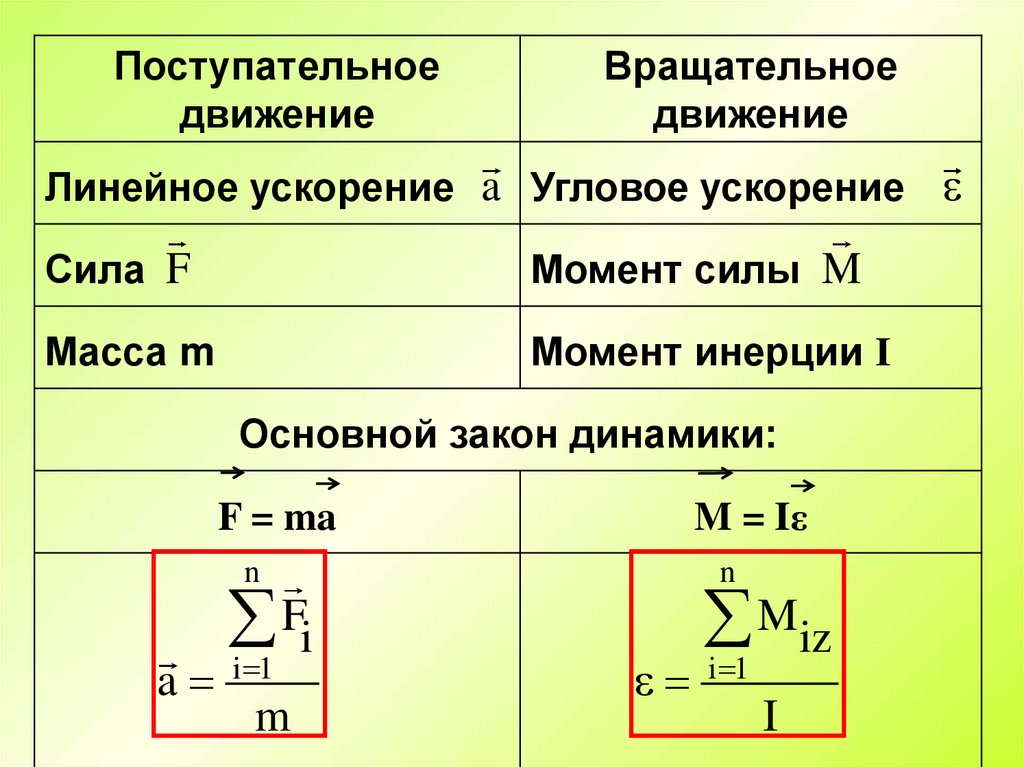
Поступательноедвижение
Вращательное
движение
Линейное ускорение a Угловое ускорение
Сила F
Момент силы M
Масса m
Момент инерции I
Основной закон динамики:
F = ma
M = Iε
n
a
Fi
i 1
m
n
Miz
i 1
I
32. Контрольные вопросы
Дайте определение вращательного движения.Дайте определение угловой скорости.
Дайте определение углового ускорения.
Какова связь между угловой и линейной скоростью?
Чему равно центростремительное ускорение?
Какова связь между линейным и угловым
ускорением материальной точки?
7. Что такое период вращения?
8. Что показывает частота вращения?
9. Какова связь между периодом вращения и угловой
скоростью?
1.
2.
3.
4.
5.
6.
33. Контрольные вопросы
10. Дайте определение момента силы.11. Что называется плечом силы?
12. Что такое момент инерции материальной точки?
13 . Какое свойство тела характеризует его момент
инерции?
14. Сформулируйте основной закон динамики
вращательного движения?
33
34.
Задача: Колесо автомашины вращается равнозамедленно. За время t=2 мин оно изменило частоту вращения от 240 до 60 мин-1. Определить:1) угловое ускорение колеса; 2) число полных оборотов,
сделанных колесом за это время. [1) 0,157 рад/с2; 2) 300]
34
35.
Задача: На шкив радиусом 0,5 м намотан шнур, кконцу которого привязана гиря массой 10 кг. Груз
опускается с ускорением 2 м/с2. Найти момент инерции
шкива.
35
36.
Задача: К ободу диска радиусом 20 см с моментоминерции 2 кг∙м2 приложена касательная сила 50 Н.
Какова будет угловая скорость через 10 с после начала
действия этой силы, если момент сил трения 8 Нм?
36


















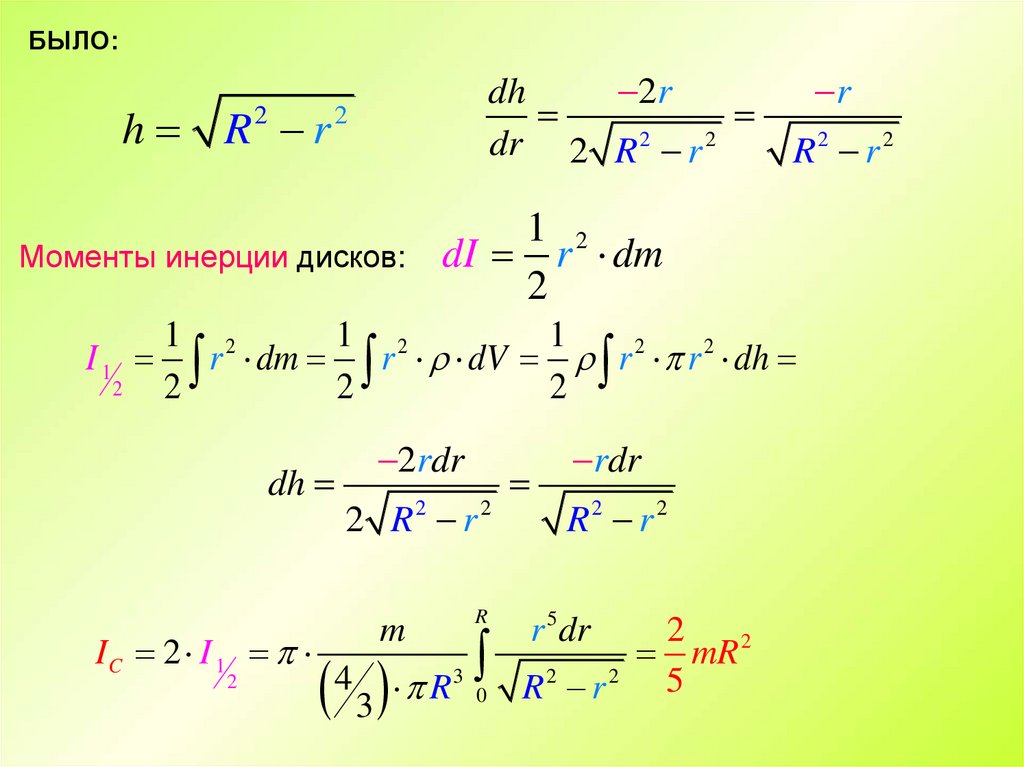





 Физика
Физика








