Введение в теорию четырёхполюсников линейных цепей переменного тока

1. С.Н. Охулков ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА

Федеральное агентство по образованию
Нижегородский государственный технический университет
им. Р.Е. АЛЕКСЕЕВА
С.Н. Охулков
ЭЛЕКТРОТЕХНИКА
И ЭЛЕКТРОНИКА
Кафедра “Теоретическая и общая
электротехника”
Для студентов электротехнических
специальностей всех форм обучения

2.

Автозаводская высшая школа управления и технологий
Очная и заочная форма обучения
- Автомобили и автомобильное хозяйство
- Автомобиле- и тракторостроение
Технология машиностроения
г. Нижний Новгород, ул. Лескова, 68, т. (831) 256-02-10

3. Тема 5

ВВЕДЕНИЕ В ТЕОРИЮ
ЧЕТЫРЁХПОЛЮСНИКОВ
ЛИНЕЙНЫХ ЦЕПЕЙ
ПЕРЕМЕННОГО ТОКА

4.

Четырехполюсник –
это устройство, имеющее четыре контакта:
два входных контакта используются для
подключения источника сигнала
и два выходных - для подключения нагрузки
см. схему

5.

Четырехполюсник

6.

Четырехполюсники широко применяются в системах
информации. Четырехполюсниками являются усилители,
фильтры, линии связи и т.д.
Четырехполюсник,
содержащий только
линейные элементы,
называется
Если внутри четырехполюсника
есть нелинейные или
параметрические элементы,
то четырехполюсник будет
линейным.
нелинейным
или
параметрическим.

7.

Четырехполюсник, не содержащий источников
напряжения или тока,
называется
ПАССИВНЫМ
АКТИВНЫЕ
четырехполюсники
содержат источники напряжения или тока

8.

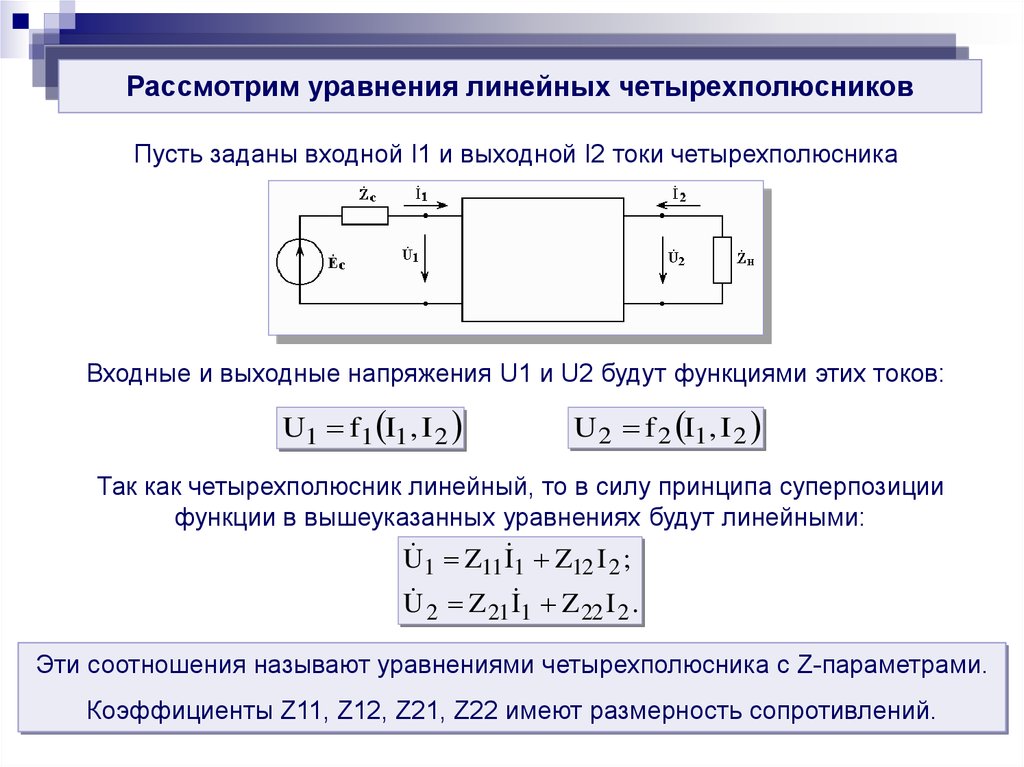
Рассмотрим уравнения линейных четырехполюсников
Пусть заданы входной I1 и выходной I2 токи четырехполюсника
Входные и выходные напряжения U1 и U2 будут функциями этих токов:
U1 f1 I1 , I 2
U 2 f 2 I1 , I 2
Так как четырехполюсник линейный, то в силу принципа суперпозиции
функции в вышеуказанных уравнениях будут линейными:
Z I Z I ;
U
1
11 1
12 2
Z I Z I .
U
2
21 1
22 2
Эти соотношения называют уравнениями четырехполюсника с Z-параметрами.
Коэффициенты Z11, Z12, Z21, Z22 имеют размерность сопротивлений.

9.

Если заданы напряжения
четырехполюсника U1 и U2,
то можно получить уравнения:
I1 Y11 U1 Y12 U 2 ;
I 2 Y21 U1 Y22 U 2 .
Это соотношение называют
уравнениями четырехполюсника с Y-параметрами
Коэффициенты Y11, Y12, Y21, Y22
имеют размерность проводимостей

10.

При заданных I1 и U2
получаем уравнения с
h-параметрами:
где
U1 h 11 I1 h 12 U 2 ;
I 2 h 21 I1 h 22 U 2 .
h11 имеет размерность сопротивления;
h22 имеет размерность проводимости;
h12, h21 – безразмерные коэффициенты.
Коэффициенты пропорциональности Z, Y, h
характеризуют внутреннюю структуру
четырехполюсника,
которая проявляется через взаимосвязь
входных и выходных токов и напряжений.

11.

Из анализа уравнений четырехполюсника легко
получить физический смысл параметров
четырехполюсника.
Для Z-параметров:
Z11 = U1/I1,
при I2 = 0 – входное сопротивление при холостом ходе на выходе;
Z12 = U1/I2,
при I1 = 0 – сопротивление обратной связи;
Z21 = U2/I1,
при I2 = 0 – сопротивление прямой передачи;
Z22 = U1/I2,
при I1 = 0 – выходное сопротивление при холостом ходе на входе.

12.

Для Y-параметров:
Y11 = I1/U1,
при U2 = 0 – входная проводимость при коротком замыкании на
выходе;
Y12 = I1/U2,
при U1 = 0 – проводимость обратной связи;
Y21 = I2/U1,
при U2 = 0 – проводимость прямой передачи;
Y22 = I2/U2,
при U1 = 0 – выходная проводимость при коротком замыкании на
входе.

13.

Для h-параметров:
h11 = U1/I1,
при U2 = 0 – входное сопротивление при коротком замыкании на
выходе;
h12 = U1/U2,
при I1 = 0 – коэффициент обратной связи по напряжению;
h21 = I2/I1,
при U2 = 0 – коэффициент прямой передачи по току;
h22 = I2/ U2,
при I1 = 0 – выходная проводимость при холостом ходе на входе.
Название параметра указывает на способ его
экспериментального определения или расчета
методом комплексных амплитуд

14.

Четырехполюсники
в основном используются
в системах передачи сигналов.
Для анализа прохождения сигналов через
четырехполюсник вводятся
передаточные функции
четырехполюсника.

15.

Передаточные функции четырехполюсника
U
KU U
2
1
– комплексный коэффициент передачи по
напряжению
K I I 2 I1
– комплексный коэффициент передачи по току
K P Pвых Pвх
– коэффициент передачи активной мощности
I
Z вх U
1 1
– комплексное входное сопротивление
I
Z вых U
2 2
– комплексное выходное сопротивление

16.

Наиболее часто используемыми передаточными функциями
являются коэффициент передачи по напряжению, входное и
выходное сопротивление.
Рассмотрим расчет этих функций
при известных параметрах
четырехполюсника

17.

Пусть известны Y-параметры четырехполюсника.
Используя уравнение I2 = Y21U1 + Y22U2 и формулу закона Ома
для нагрузки U2 = – ZнI2, получим выражение для
комплексного коэффициента передачи по напряжению:
K U Y21 Y22 Yн
где Yн = 1/Zн.
Используя формулу для входной проводимости Yвх = I1/U1
и деля уравнение I1 = Y11U1 + Y12U2 на напряжение U1, найдем
водную проводимость четырехполюсника:
Yвх Y11 Y12 Y21 Yн Y22
Аналогично, выходная проводимость четырехполюсника:
Yвых Y22 Y21 Y12 Y11 Yс
где Yc = 1/Zc.

18.

Рассмотрим методику расчета частотных характеристик
линейных четырехполюсников.
Комплексный коэффициент передачи по напряжению КU(j ),
в дальнейшем просто К(j ), представляет собой запись двух
характеристик: амплитудно-частотной (АЧХ) и фазочастотной
(ФЧХ):
K j K1 ( ) jK 2 ( ) K( )e j ( )
Первая характеристика К( ) выражается модулем
комплексного коэффициента передачи,
а вторая ( ) – его аргументом (фазой):
K( ) K12 ( ) K 22 ( )
K 2 ( )
( ) arctg
K1 ( )

19.

Для цепей с сосредоточенными параметрами частотные
характеристики могут быть представлены в виде отношения
двух полиномов:
M
a m j
K ( j )
m
A( j ) m 0
N
B( j )
n
b n j
n 0
Если обозначить j = р, то вышеприведенное выражение
можно записать в виде:
M
a mpm
K ( p)
A ( p) m 0
N
B(p)
bnpn
n 0
Это выражение называется
операторным коэффициентом передачи

20.

Исследование свойств полиномов А(р) и В(р) позволяет ответить на
многие вопросы, связанные с определением реакции линейной цепи на
сложное воздействие. В этой лекции рассматриваются частотные
характеристики в плане их применения к анализу цепей при
синусоидальном воздействии.
Если Zc << Z11, а Z22 << Zн
(см. схему),
то операторный
коэффициент передачи
приблизительно можно
определить без учета
сопротивлений источника
сигнала и нагрузки:
Z 22 p Z вых р
K p
Z11 p Z вх р
Рассмотрим примеры определения частотных характеристик простейших
четырехполюсников, для которых выполняется это условие

21.

Пример 1
Найти выражения амплитудночастотной и фазочастотной
характеристик коэффициента
передачи напряжения для
четырехполюсника, изображенного
справа.
RC-фильтр верхних частот
первого порядка
Операторный коэффициент
передачи по напряжению:
K p
Комплексный
коэффициент передачи (р = j ):
K j
pRC
R
R 1 pC 1 pRC
j RC
1 j RC
2 R 2 C 2
RC
Комплексный коэффициент передачи
в алгебраической форме:
K j
Модуль коэффициента передачи:
K
Фазовый сдвиг между выходным и
входным напряжением:
1
U U arctg
2
1
RC
1 2 R 2 C 2
j
1 2 R 2 C 2
RC
1 2 R 2 C 2

22.

Продолжение примера 1
Графики, рассчитанные по полученным формулам
АЧХ RC-фильтра верхних
частот первого порядка
ФЧХ RC-фильтра верхних
частот первого порядка

23.

Пример 2
Найти выражения амплитудночастотной и фазочастотной
характеристик коэффициента
передачи напряжения для
четырехполюсника, изображенного
справа.
RC-фильтр нижних
частот первого порядка
Операторный коэффициент
передачи по напряжению:
K p
Комплексный
коэффициент передачи (р = j ):
K j
Комплексный коэффициент передачи
в алгебраической форме:
K j
1 pC
1
R 1 pC 1 pRC
1
1 j RC
1
1 2 R 2 C 2
j
RC
1 2 R 2 C 2
Модуль коэффициента передачи:
K
Фазовый сдвиг между выходным и
входным напряжением:
U U arctg RC
2
1
1
1 2 R 2 C 2

24.

Продолжение примера 2
Графики, рассчитанные по полученным формулам
АЧХ RC-фильтра нижних
частот первого порядка
ФЧХ RC-фильтра нижних
частот первого порядка

25.

Пример 3
Найти выражение амплитудночастотной характеристики
коэффициента передачи
четырехполюсника, изображенного
справа.
Полосовой RLC-фильтр
второго порядка
Операторный коэффициент
передачи по напряжению:
K p
Комплексный
коэффициент передачи (р = j ):
K j
pRC
R
pL 1 pC R p 2 LC pRC 1
j RC
1 2 LC j RC

26.

Продолжение примера 3
Для определения модуля коэффициента передачи К( )
воспользуемся известным положением теории комплексных чисел
о том, что произведение комплексного числа на комплексносопряженное число равно квадрату его модуля:
K 2
j RC
j RC
1 2 LC j RC 1 2 LC j RC
K
2
K
2 R 2 C 2
1 2 LC 2 2 R 2C 2
RC
1 2 LC 2 2 R 2C 2
Очевидно, что коэффициент передачи на резонансной частоте
0 1 LC
будет максимальным, К( 0) = 1.

27.

Продолжение примера 3
АЧХ, рассчитанная по формуле
K
RC
1 2 LC 2 2 R 2C 2
АЧХ полосового RLC-фильтра
второго порядка

28.

Пример 4
Найти выражение амплитудночастотной характеристики
четырехполюсника, изображенного
справа.
Режекторный RLC-фильтр
второго порядка
Операторный коэффициент
передачи по напряжению:
Комплексный
коэффициент передачи (р = j ):
Модуль коэффициента передачи:
1 pC pL
p 2 LC 1
K p
R 1 pC pL p 2 LC pRC 1
K j
K
1 2 LC
1 2 LC j RC
1 2 LC
1 2 LC 2 2 R 2 C 2

29.

Продолжение примера 4
Очевидно, что коэффициент передачи на резонансной частоте
0 1 LC
будет минимальным, К( 0) = 0.
АЧХ, рассчитанная по формуле
K
1 2 LC
1 2 LC 2 2 R 2 C 2
АЧХ режекторного RLC-фильтра
второго порядка

30.

В современных системах передачи информации широко
используется частотный принцип разделения сигналов.
В соответствии с этим каждому сигналу соответствует своя
полоса частот, которая определяется спектром сигнала.
Важнейшую роль при обработке сигналов
в таких системах играют
электрические фильтры.
Электрический частотный фильтр
( в дальнейшем просто фильтр) –
это четырехполюсник, коэффициент передачи которого
зависит от частоты. Фильтр пропускает сигналы только в
определенной полосе частот; сигналы (помехи), частоты
которых не попадают в эту полосу, подавляются.

31.

По диапазону пропускаемых частот
фильтры делятся на
фильтры нижних частот (ФНЧ),
фильры верхних частот (ФВЧ),
полосовые фильтры (ПФ),
режекторные (РФ) или заграждающие (ЗФ)
фильтры.

32.

Условные обозначения (УГО) фильтров

33. Рекомендуемая литература

1. Алтунин Б.Ю., Панкова Н.Г. Теоретические основы электротехники:
Комплекс учебно - методических материалов: Часть 1 / Б.Ю. Алтунин,
Н.Г. Панкова; НГТУ им. Р.Е. Алексеева. Н.Новгород, 2007.-130 с.
2. Алтунин Б.Ю., Кралин А.А. Электротехника и электроника: комплекс
учебно-методических материалов: Ч.1/ Б.Ю. Алтунин, А.А. Кралин;
НГТУ
им. Р.Е. Алексеева. Н.Новгород, 2007.-98 с.
3. Алтунин Б.Ю., Кралин А.А. Электротехника и электроника: комплекс
учебно-методических материалов: Ч.2/ Б.Ю. Алтунин, А.А. Кралин;
НГТУ
им. Р.Е. Алексеева. Н.Новгород, 2008.-98 с
4. Касаткин, А.С. Электротехника /А.С. Касаткин, М.В. Немцов.-М.:
Энергоатомиздат, 2000.
5. Справочное пособие по основам электротехники и электроники
/под. ред. А.В. Нетушила.-М.: Энергоатомиздат, 1995.
6. Манаев Е.И. Основы радиоэлектроники.-3-е изд., перераб. И доп.-М.:
Радио и связь, 1990.-512 с.: ил.
7. Новожилов, О. П. Электротехника и электроника: учебник / О. П.
Новожилов. – М.: Гардарики, 2008. – 653 с.
Электротехника и электроника

34. Тема 5 Закончена

Благодарю за внимание