Математическая логика и теория алгоритмов. Введение. (Глава 1)

1.

МАТЕМАТИЧЕСКАЯ ЛОГИКА
И ТЕОРИЯ АЛГОРИТМОВ
Кафедра
Тесты:
Баллы:
Прикладной математики и
Информатики
по 1-2 гл. + к.р. + Итог.Тест
30
+ 30 +
40
= 100.
1

2.

МАТЕМАТИЧЕСКАЯ ЛОГИКА
И ТЕОРИЯ АЛГОРИТМОВ
&
1. Мендельсон Э. Введение в математическую логику.
2. Судоплатов С.В., Овчинникова Е. В. Математическая логика и теория
алгоритмов. Учебник, 2004.
3. Шапорев С.Д. Математическая логика. Курс лекции и практических
занятий. Учебное пособие, 2005.
4. Галиев Ш. И. Математическая логика и теория алгоритмов. Учебное
пособие, 2004.
2

3.

ИЗУЧАЕМЫЕ РАЗДЕЛЫ
1.
Логика высказываний
2.
Логика предикатов
3.
Логическое следствие и метод резолюций
4.
Теория алгоритмов
5.
Дедуктивные теории
6.
Неклассические логики
7.
Сложность вычислений
3

4.

СТАНОВЛЕНИЕ МАТЕМАТИЧЕСКОЙ ЛОГИКИ
Логика понимается как наука о способах доказательств и
опровержений.
Математическая логика – это логика, развиваемая с
помощью математических методов.
1.
Все люди смертны. Сократ – человек. Следовательно,
Сократ – смертен.
2.
Все
котята
любят
играть.
Мурка
–
котенок.
Следовательно, Мурка любит играть.
Оба эти вывода имеют одну и ту же форму:
Все А суть В; С есть А; следовательно, С есть В.
Эти выводы истинны в силу своей формы, независимо от
содержания.
4

5.

ПАРАДОКС БРАДОБРЕЯ
"To shave or not to shave…"
В одном полку был полковой парикмахер,
которого называют брадобреем.
Однажды командир приказал ему брить
тех и только тех, кто не бреется сам.
Брадобрей, получив приказ, сначала
обрадовался, потому что многие солдаты
умели бриться сами, а потом сел на пенек и
задумался: а что ему с собой-то делать?
Ведь если он будет брить себя, то
нарушит приказ командира не брить тех, кто
бреется сам. Брадобрей уже решил было, что брить себя не будет.
Но тут его осенила мысль, что если он сам себя брить не будет, то
окажется, что он сам не бреется, и по приказу командира он должет все-таки
себя побрить...
5

6.

6

7.

Основатель
математической
логики
7

8.

Принципиальное и прикладное значение математической логики
Принципиальное значение – обоснование математики
Прикладное значение. Применяется для следующих целей:
анализа и синтеза цифровых вычислительных машин и других
дискретных автоматов, в том числе и интеллектуальных систем;
анализа и синтеза формальных и машинных языков, для анализа
естественного языка;
проверки правильности программ и электронных схем;
анализа и формализации интуитивного понятия вычислимости;
создания экспертных систем для решения сложных проблем;
выяснения существования механических процедур для решения
задач определённого типа;
анализа проблем сложности вычислений.
8

9.

Глава 1
ЛОГИКА ВЫСКАЗЫВАНИЙ
§ 1. Высказывания, логические операции
Высказывание – повествовательное
предложение, которое истинно либо ложно.
9

10.

ВЫСКАЗЫВАНИЯ, ЛОГИЧЕСКИЕ ОПЕРАЦИИ
Высказывания:
2 2 = 4, 2 + 2 = 5, 2 > 1, 1 = 2, 3 2.
Не высказывания: sin x > 0,
x < y,
x + y > z,
«данное предложение ложно».
Операции:
А
В
А
А&В
А В
А В
А В
Л
Л
И
Л
Л
И
И
Л
И
И
Л
И
И
Л
И
Л
Л
Л
И
Л
Л
И
И
Л
И
И
И
И
- отрицание,
& - конъюнкция;
- импликация;
- эквивалентность.
-дизъюнкция;
10

11.

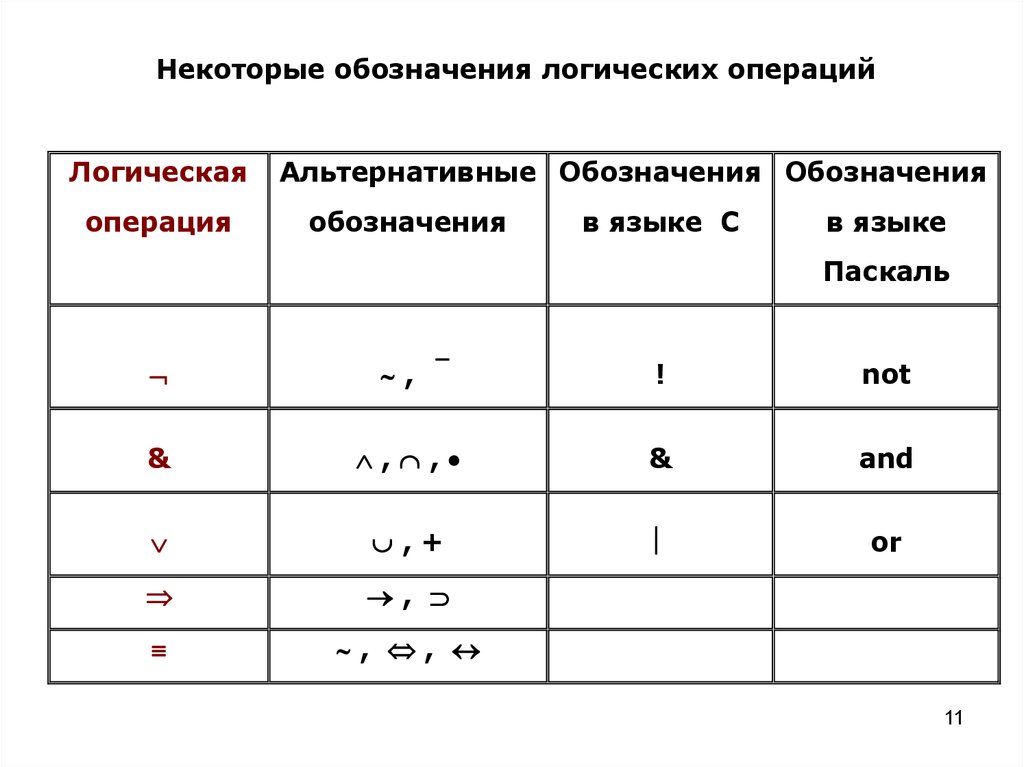
Некоторые обозначения логических операций
Логическая
операция
Альтернативные Обозначения Обозначения
обозначения
в языке С
в языке
Паскаль
,
!
not
&
, ,
&
and
,+
or
,
, ,
11

12.

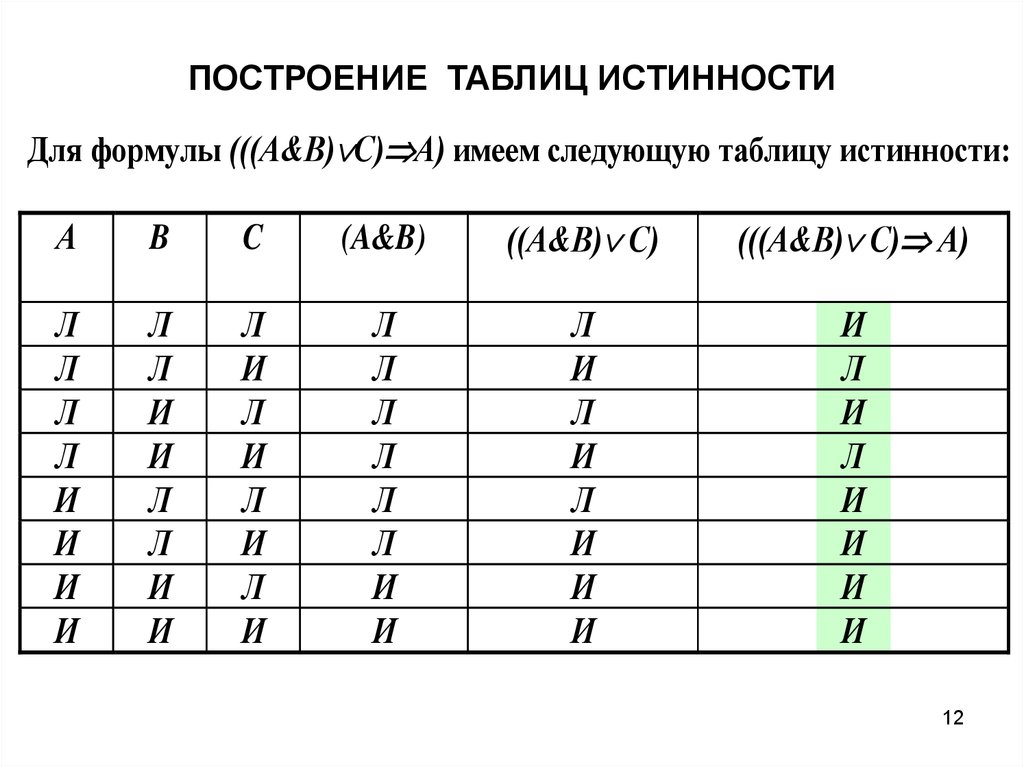
ПОСТРОЕНИЕ ТАБЛИЦ ИСТИННОСТИ
Для формулы (((А&В) С) А) имеем следующую таблицу истинности:
А
B
C
(A&B)
((А&В) С)
(((А&В) С) А)
Л
Л
Л
Л
И
И
И
И
Л
Л
И
И
Л
Л
И
И
Л
И
Л
И
Л
И
Л
И
Л
Л
Л
Л
Л
Л
И
И
Л
И
Л
И
Л
И
И
И
И
Л
И
Л
И
И
И
И
12

13.

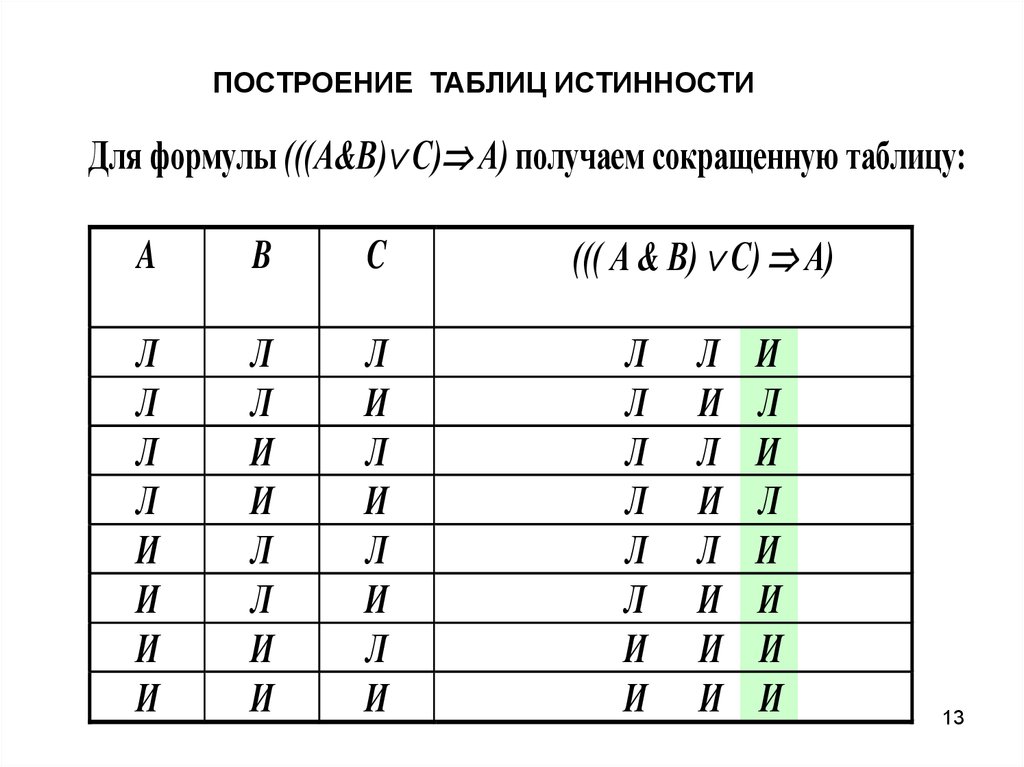
ПОСТРОЕНИЕ ТАБЛИЦ ИСТИННОСТИ
Для формулы (((А&В) С) А) получаем сокращенную таблицу:
A
B
C
Л
Л
Л
Л
И
И
И
И
Л
Л
И
И
Л
Л
И
И
Л
И
Л
И
Л
И
Л
И
((( А & В) С) А)
Л
Л
Л
Л
Л
Л
И
И
Л
И
Л
И
Л
И
И
И
И
Л
И
Л
И
И
И
И
13

14.

СОСТАВЛЕНИЕ ТАБЛИЦ ИСТИННОСТИ
Если сложное высказывание имеет n атомарных
высказываний, то его таблица истинности имеет
2
n
строк значений этого сложного высказывания.
Для n = 1 таблица имеет 2 строки;
n = 2 таблица имеет 4 строки;
n = 3 таблица имеет 8 строк и т.д.
14

15.

ПРОПОЗИЦИОНАЛЬНЫЕ ФОРМЫ ФОРМУЛЫ ЛОГИКИ ВЫСКАЗЫВАНИЙ
, & , , , - пропозициональные связки.
А1 , А2 , А3 ,… - пропозициональные буквы.
Определение пропозициональной формы:
1) каждая пропозиц. буква - пропозициональная форма,
2) если A и B пропозициональные формы, то ( A ) , (A & B ),
(A B ), (A B ), (A B ) тоже пропозиц. формы,
3) только те выражения являются пропозиц. формами,
для которых это следует из пп.1), 2).
Примеры: A,
( В ), ( А & ( В )), (( А & В) ( C )),
Упрощения в записях:
((( А) В ) С).
а) , б) , в): , & , , , .
15

16.

Пропозициональные формы –
формулы логики высказываний
Определение формул с помощью нормальных форм Бэкуса. Пусть Р
множество пропозициональных букв (атомов).
формула : = A
для любого A из Р
формула : = ( формула) ( формула & формула)
( формула формула) ( формула формула)
( формула формула)
Пр. : A, В, ( В), (A &( B)), ((A&B) С), (A (B C))
A, В, В,
A & B,
A&B С,
A (B C)
Атом или атомарная формула : = пропозициональная
буква
Пр.:
А,
В,
С, … .
16

17.

УПРОЩЕНИЯ В ЗАПИСЯХ
Упрощения в записях: а) , б) , в):
, &, , , .
Примеры: A, ( В ), ( А & ( В )), (( А & В) ( C )), ((( А) В ) С).
Сокр. запись: A, В, А & В,
Примеры:
( А & (А В )),
Сокр. запись: А & (А В ),
А & В C,
А В С.
( А (В C )),
( ( В С)).
А (В C ),
( В С).
17

18.

ТАВТОЛОГИИ ( ОБЩЕЗНАЧИМЫЕ ФОРМУЛЫ ). ПРОТИВОРЕЧИЯ
Тавтология ( Т ) - пропоз. форма, которая всегда принимает знач. И .
Примеры:
А А,
А А,
(А В) (В А).
Противоречие ( П ) - пропозиц. форма, которая всегда = Л .
Примеры: А & А,
(А А),
А А.
Теорема 1.1. Если A и A B - тавтологии, то B - тавтология.
Теорема 1.2. Если A есть тавтология, содержащая А1, А2,..., Аn, и B
получается из A подстановкой в A форм A 1, A 2 ,..., A n вместо
букв А1, А2 ,..., Аn
соответственно, то B
есть тавтология, т.е.
подстановка в тавтологию приводит к тавтологии.
Форма называется выполнимой, если она принимает значения И
хотя бы для одной совокупности значений пропозициональных букв,
в нее входящих.
18

19.

ПРОБЛЕМА РАЗРЕШИМОСТИ ЛОГИКИ ВЫСКАЗЫВАНИЙ
Проблема разрешимости логики высказываний: указать единый
способ (алгоритм), позволяющий для каждой формы A за конечное
число действий выяснить, является ли A тавтологией или нет.
Имея такой способ, мы сможем узнавать, будет ли
Если
A выполнимой или нет.
A тавтология, то A противоречие, следовательно, A невыполнима.
Если A не тавтология, то A выполнима.
Проблема
разрешимости
логики
высказываний
разрешима,
например, используя таблицу истинности можно выяснить, будет
форма тавтологией или нет.
19

20.

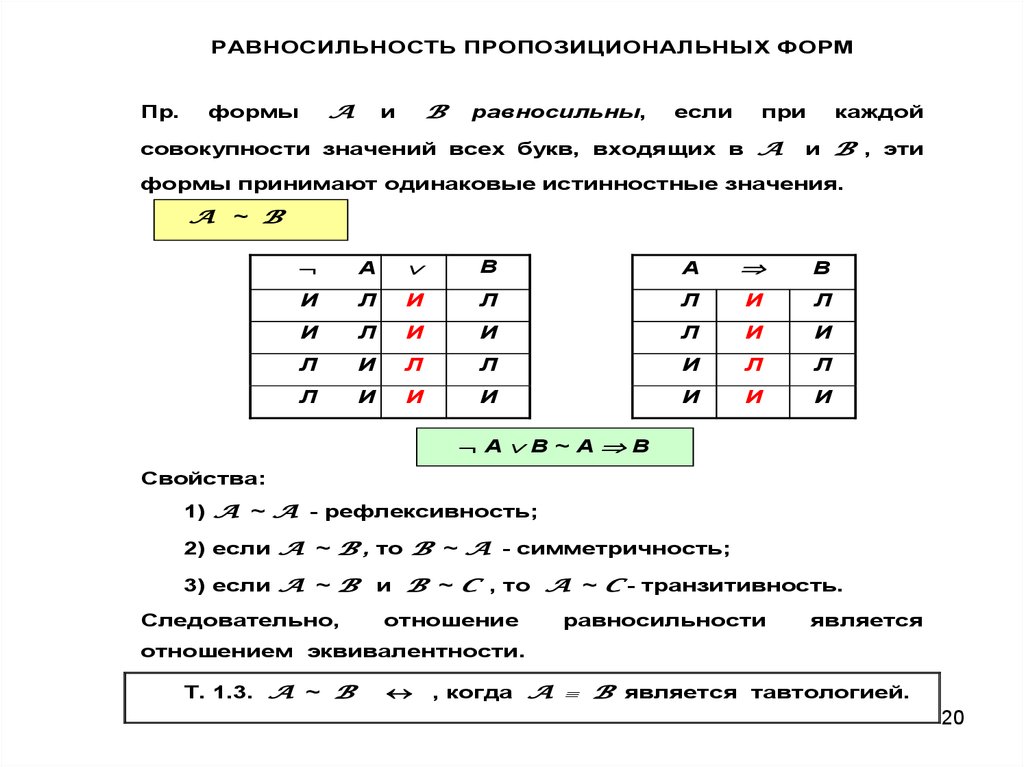
РАВНОСИЛЬНОСТЬ ПРОПОЗИЦИОНАЛЬНЫХ ФОРМ
Пр.
A
формы
B
и
равносильны,
если
при
совокупности значений всех букв, входящих в A
каждой
и B , эти
формы принимают одинаковые истинностные значения.
A
~ B
A
B
A
B
И
Л
И
Л
Л
И
Л
И
Л
И
И
Л
И
И
Л
И
Л
Л
И
Л
Л
Л
И
И
И
И
И
И
A В~A B
Cвойства:
1) A ~ A - рефлексивность;
2) если A ~ B , то B ~ A - симметричность;
3) если A ~ B
Следовательно,
и B ~ C , то A ~ C - транзитивность.
отношение
равносильности
является
отношением эквивалентности.
Т. 1.3. A ~ B
, когда A B является тавтологией.
20

21.

ОСНОВНЫЕ
СООТНОШЕНИЯ
закон двойного отрицания.
1) ( А) ~ А 2) A & B ~ B & A;
законы коммутативности;
3) A B ~ B A;
4) (A & B) & C ~ A & (B & C);
законы ассоциативности;
5) (A B) C ~ A ( B C );
первый закон дистрибутивности;
6) А&(В С) ~ А&В А&С 7) А В&С ~ (А В)&(А С) - второй закон дистрибутивности;
8) (А&В) ~ А В,
- законы де Моргана;
9) (А В) ~ А& В,
10) А&А ~ А, законы идемпотентности;
11) А А ~ А,
21

22.

ОСНОВНЫЕ
12)
13)
14)
15)
16)
17)
18)
19)
СООТНОШЕНИЯ
А А&В ~ А;
- законы поглощения;
А & (А В ~ А;
А А ~ Т - закон исключенного третьего;
А & А ~ П - закон противоречия;
А & Т ~ А;
А Т ~ Т;
А & П ~ П; свойство операций с Т и с П;
А П ~ А;
22

23.

Основные соотношения
1) ( А) ~ А.
2) A & B ~ B & A;
3) A B ~ B A;
4) (A & B) & C ~ A & (B & C);
5) (A B) C ~ A ( B C );
6) А&(В С) ~ А&В А&С ;
7) А В&С ~ (А В)&(А С);
8) (А&В) ~ А В,
9) (А В) ~ А& В,
10) А&А ~ А,
11) А А ~ А,
12) А А&В ~ А;
13) А&(А В ~ А;
14) А А ~ Т;
15) А& А ~ П;
16) А&Т ~ А;
17) А Т ~ Т;
18) А&П ~ П;
19) А П ~ А;
20) А В ~ В А
23

24.

ЗАВИСИМОСТИ МЕЖДУ СВЯЗКАМИ
А В ~ (А В) & (В А);
А В ~ А В;
А В ~ ( А В) & ( В А);
А & В ~ ( A В);
А В ~ ( А & В);
А В ~ А В.
Теорема 1.4. Для каждой пропозициональной формы A существует
равносильная ей форма, содержащая только связки , &,
связка относится только к пропозициональным буквам.
,
причем
Теорема 1.5. Для каждой пропозициональной формы A существует
равносильная ей форма, содержащая либо только связки , &, либо
, , либо ,
.
24

25.

ДИЗЪЮНКТИВНЫЕ И КОНЪЮНКТИВНЫЕ
НОРМАЛЬНЫЕ ФОРМЫ
Элементарные суммы: А В,
С А,
Элементарные произведения: А&В,
А В А С.
В&С,
А&С&А&В.
Дизъюнктивные нормальные формы (д.н.ф.): В&С А&D, А В&С,
А&С А&В& С.
Теорема
1.7.
Для
каждой
пропозициональной
формы
существует
равносильная ей д.н.ф. (не единственная).
Конъюнктивные нормальные формы (к.н.ф.): (А В) & (С D), (А В С)& B.
Теорема
1.9.
Для
каждой
пропозициональной
формы
существует
равносильная ей к.н.ф. (не единственная).
25

26.

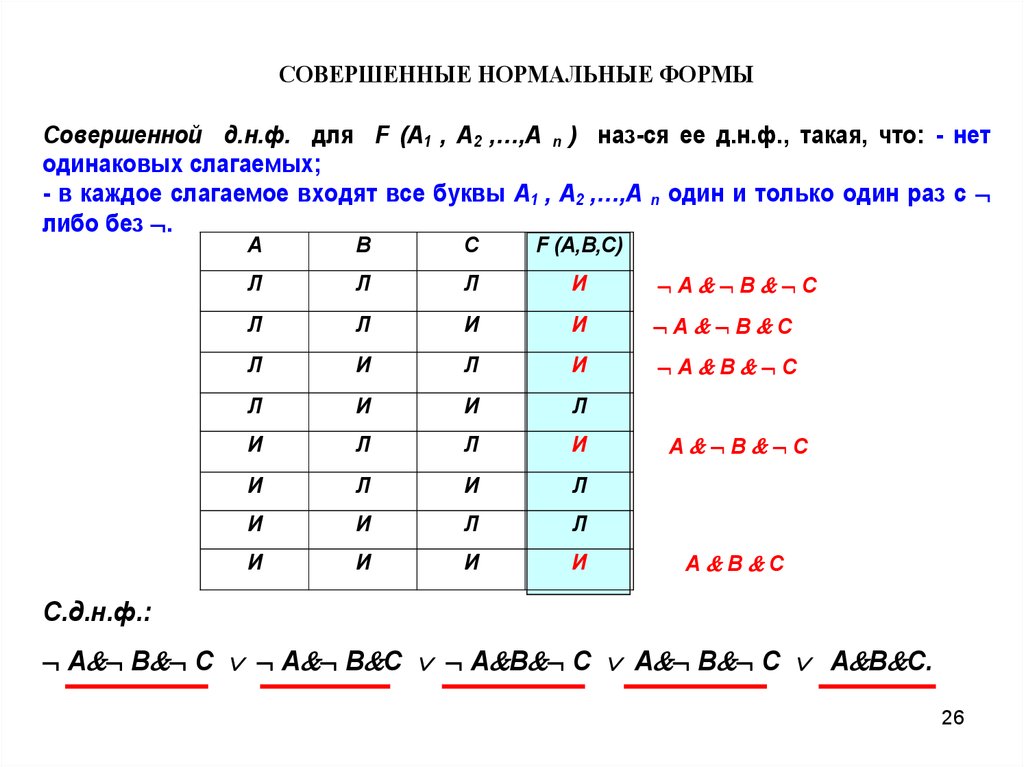
СОВЕРШЕННЫЕ НОРМАЛЬНЫЕ ФОРМЫ
Совершенной д.н.ф. для F (A1 , A2 ,…,A n ) наз-ся ее д.н.ф., такая, что: - нет
одинаковых слагаемых;
- в каждое слагаемое входят все буквы A1 , A2 ,…,A n один и только один раз с
либо без .
А
В
С
F (А,В,С)
Л
Л
Л
И
А В С
Л
Л
И
И
А В С
Л
И
Л
И
А В С
Л
И
И
Л
И
Л
Л
И
И
Л
И
Л
И
И
Л
Л
И
И
И
И
А В С
А В С
С.д.н.ф.:
А В С А В С А В С А В С А В С.
26

27.

СОВЕРШЕННЫЕ НОРМАЛЬНЫЕ ФОРМЫ
Совершенной к.н.ф. для F (А1 , А2 ,…,Аn ) называется ее к.н.ф., такая, что:
-нет одинаковых множителей;
-в каждое мн. входят все перем. А1 , А2 ,…,А n один и только один раз с
либо без .
С.к.н.ф.:
А
В
С
F (А,В,С)
Л
Л
Л
И
Л
Л
И
И
Л
И
Л
И
Л
И
И
Л
И
Л
Л
И
И
Л
И
Л
А В С
И
И
Л
Л
А В С
И
И
И
И
А В С
( А В С ) ( А В С ) ( А В С ).
27

28.

СОВЕРШЕННЫЕ НОРМАЛЬНЫЕ ФОРМЫ
Совершенной к.н.ф. для F (А1 , А2 ,…,Аn ) называется ее к.н.ф., такая, что:
-нет одинаковых множителей;
-в каждое мн. входят все перем. А1 , А2 ,…,А n один и только один раз с
либо без .
С.к.н.ф.:
А
В
С
F (А,В,С)
Л
Л
Л
И
Л
Л
И
И
Л
И
Л
И
Л
И
И
Л
И
Л
Л
И
И
Л
И
Л
А В С
И
И
Л
Л
А В С
И
И
И
И
А В С
( А В С ) ( А В С ) ( А В С ).
28