Похожие презентации:
Оценка достоверности статистических параметров. Статистический анализ вариации количественных признаков
1. Оценка достоверности статистических параметров. Статистический анализ вариации количественных признаков
Лекция 22. Каждое отдельное явление, взятое само по себе (длина листа на дереве) является случайным. Но взятые в массе они обнаруживают
статистическиезакономерности.
3. Вероятность – это возможность осуществления определенного события в некотором количестве случаев из общего числа возможных.
Вероятность варьирует от 0 до 1.p=m/N, где m- число благоприятных
факторов, N – число равновозможных
случаев
4. Теорема сложения вероятностей
Для независимых друг от друга событий, которыесовершенно несовместимы.
Например, на клумбе растут 20 красных, 30 синих
и 40 белых астр. Какова вероятность сорвать в
темноте окрашенную (синюю или красную)
астру?:
20 30
p
0,56
90 90
5. Теорема умножения вероятностей.
Относится к таким независимымсобытиям,
р=
которые следуют друг за другом и также
независимы друг от друга.
Например, какова вероятность наличия цифры 4
=
у двух выброшенных одновременно кубиков?
p= 1/6 *1/6 = 1/36
6. Теоретическая и эмпирическая (фактическая) вероятности.
Фактические вероятности приложимы только кконкретным совокупностям, по которым они
вычислены.
В генеральной совокупности вероятности
становятся теоретическими.
Возникает вопрос о том, насколько достоверны
статистические показатели, полученные по
выборочной совокупности, чтобы можно было по
ним судить о генеральной совокупности.
7. Распределение вероятностей
х1, х2, х3 ,…, хnр1, р2, р3 ,…, pn
Распределение - совокупность значений xi
и соответствующих им вероятностей pi .
8. Виды распределений
Биномиальное(a+b)1=a+b
(a+b)2=a2+2ab+b2
Частоты распределения отдельных классов
пропорциональны коэффициентам разложения
бинома Ньютона: (p+q)k , где p – вероятность
появления данного события, q- вероятность не
появления, k- количество классов.
Пуассона
Для очень редких событий, распределение событий
ассиметрично.
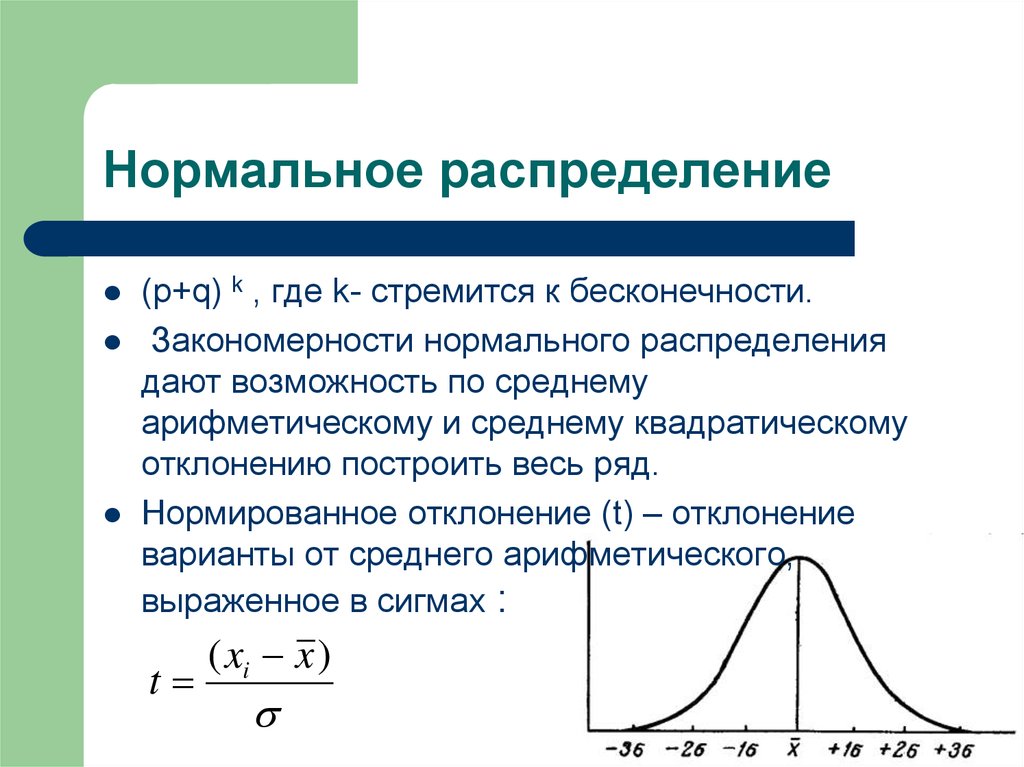
9. Нормальное распределение
(p+q) k , где k- стремится к бесконечности.Закономерности нормального распределения
дают возможность по среднему
арифметическому и среднему квадратическому
отклонению построить весь ряд.
Нормированное отклонение (t) – отклонение
варианты от среднего арифметического,
выраженное в сигмах :
t
( xi x )
10. Доверительные вероятности. Уровни значимости.
Доверительнаявероятность
Доверительный
интервал
Уровень
значимости
0,95
-1,96 σ…+1,96σ
0,05 (5%)
0,99
-2,58σ…+2,58σ
0,01 (1%)
С вероятностью 0,95 любая случайно взятая варианта будет
отклоняться от среднего арифметического не более чем на
±1,96σ, иными словами, с вероятностью 0,05 варианта будет за
пределами ±1,96σ.
Вероятности 0,95 (95%) соответствует уровень значимости 0,05
(5%). Это означает, что выход за пределы принятых границ
возможен с вероятностью 0,05, то есть, вероятность ошибочного
прогноза составляет 5%.
11. Проблема достоверности в статистике.
Чем меньше ошибка средней, тем ближевыборочное среднее к генеральному среднему.
mx
N
Доверительный интервал средней
арифметической генеральной совокупности
x tmx x tmx
При N >30 коэффициент Стьюдента t01 = 1,96 и
t05=2,58
12. При N>100
При N>100Ошибка среднего квадратического отклонения и
доверительный интервал вычисляются по
формулам:
m
2N
tm ˆ tm
Ошибка коэффициента вариации и
доверительный интервал – по формулам:
cv
cv tmcv cˆv cv tmcv
mcv
2N
13. Нулевая гипотеза (Н0) - между показателями разных выборок достоверного различия нет. Противоположная гипотеза – альтернативная
(На).Ошибка первого рода (ошибка α-типа):
отклоняется нулевая гипотеза, которая в
действительности верная.
Ошибка второго рода (ошибка β-типа):
принимается нулевая гипотеза, которая в
действительности ложная.
Мощность статистического критерия - есть
вероятность того, что будет принято правильное
решение при ложной нулевой гипотезе (1-β).
Мощность критерия зависит от объема выборки,
уровня значимости, надежности
экспериментальных методов и приборов.
14. Понятия о непараметрической статистике
Параметрические критерии основаны на том илиином законе распределения случайной
переменной.
Непараметрические критерии: 1) критерии оценки
независимости элементов выборки; 2) критерии
для оценки однородности выборок; 3) критерии
для оценки степени соответствия фактических
данных теоретически ожидаемым; 4) критерии
для оценки корреляции; 5) критерии для оценки
степени сходства между объектами по комплексу
признаков.
15. Критерии оценки независимости элементов выборки
Критерий серий, основанный на медиане.Правило преобразования: вместо варианты ставится «+», если
она больше Ме; вместо варианты ставится «-», если она меньше
Ме; если варианта равна Ме, она исключается из ряда.
Серией называют последовательность записанных подряд
одинаковых знаков «+» или «-». Серия может состоять и из
одного знака.
v - количество серий во всей последовательности знаков;
T (Тау) – количество знаков в самой длинной серии.
Нулевая гипотеза (Н0) - варианты выборки независимы;
альтернативная гипотеза (НА): варианты выборки зависимы.
Если нулевая гипотеза верна, то v - количество серий – должно
быть достаточно большим, а величина T (тау) – протяженность
самой длинной серии – должна быть малой.
16. Критерий «восходящих» и «нисходящих» серий.
Сравниваются значения двух рядомрасположенных вариант (пары): «xi» и «xi+1»:
если разность (xi+1-xi)>0, то ставится знак «+»;
если разность (xi+1-xi)<0, то знак «-»; если
xi+1=xi, то никакой знак не ставится.
Нулевая гипотеза принимается если
1
3
(2 N 1) tst
16n 29
90
T (тау) <5 (при N<26); или 6 (при 27<N<153);
или7 (при 154<N<1170)
17. Критерии однородности выборок.
Однородность выборок означаетвозможность считать их выбранными из
одной и той же генеральной совокупности.
К таким критериям относятся: критерий
Манна-Уитни, критерий Уилкоксона,
критерий Краскела-Уоллиса.
















 Математика
Математика








