Статистические гипотезы и достоверность статистических характеристик

1. СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ И ДОСТОВЕРНОСТЬ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК

2. ЦЕЛИ:

1. Ознакомиться с понятием
«статистическая гипотеза».
2. Изучить основной принцип
проверки статистических гипотез.
3. Изучить алгоритм выбора
критерия для сравнения двух
средних арифметических
генеральных совокупностей.

3.

1. Статистические гипотезы
(понятие, цель).
2. Проверка статистических
гипотез и ее основные этапы.
3. Алгоритм выбора критерия для
сравнения двух средних
арифметических генеральных
совокупностей.

4.

Гипотеза - это научное предположение,
выдвигаемое для объяснения к.-л.
явления и требующая проверки на опыте
и теоретического обоснования, чтобы
стать достоверной научной истиной
Статистической гипотезой наз.
проверяемое математическими
методами предположение относительно
статистических характеристик
результатов измерений.
(обозначение гипотезы: Н)
Н0 - нулевая гипотеза, Н1 - конкурирующая гипотеза

5. Проверка статистических гипотез

Процедура проверки гипотез сводится:
• выдвигаются две гипотезы Н0, Н1
• по выборочным данным вычисляется
значение некоторой величины - Критерий (K)
• Кнабл < > Ккрит (из табл.)
какую выбрать гипотезу?
Область принятия гипотезы
Н0
Ккрит
Критическая область
Н1
(схема односторонней критической области)
К1крит
К2крит
Критическая
область
Область
принятия гипотезы
(схема двухсторонней критической области)
Критическая
Область

6.

Н0/Н0 – приняли за достоверную Н0 и она верна
Н1/Н1 – приняли за достоверную Н1 и она верна
1)
Ошибки при проверке гипотез
Н1/Н0 – приняли за достоверную Н1, а верна Н0
(ошибка 1-го рода)
2) Н0/Н1 – приняли за достоверную Н0, а верна Н1
(ошибка 2-го рода)
Р(Н1/Н0) =
α – уровень значимости –
вероятность того, что мы приняли за
достоверную Н1, а верна Н0
α (0,1; 0,05; 0,01; 0,001)

7. Критерии для проверки гипотез

1. Параметрические
2. Непараметрические

8. Основные этапы проверки статистических гипотез

Выбор
критерия:
1. Формулировка
гипотез
(Н0 и Н1)
1. От объема выборки (малая, большая)
2. Выбор
уровня
из ряда
2. От
законазначимости
распределения
α 3.
(0,1;От
0,05;
0,01; 0,001)
степени
зависимости выборок
(зависимые
или независимые)
3. Определение
выборочного
значения
4. Известныхарактеристик
или неизвестны
статистических
(из расчета)
генеральные дисперсии ( 2ген)
4. Выбор
критерия для
5. Одинаковы
илипроверки
различны
статистических
гипотез
генеральные
дисперсии
6. Возможна
ли количественная
или
5. Сравнение
расчетного
значения критерия
качественная
оценка
(Кнабл)
с критическим
(Ккрит) для
рассматриваемого
явления
выбранного α и принятия одной из гипотез

9. Выбор критерия

Известны генеральные дисперсии ( 2ген)
x y
Z
Sx2 Sy2
(Z – критерий)
Неизвестны 2ген
Z – критерий используется как приближенный

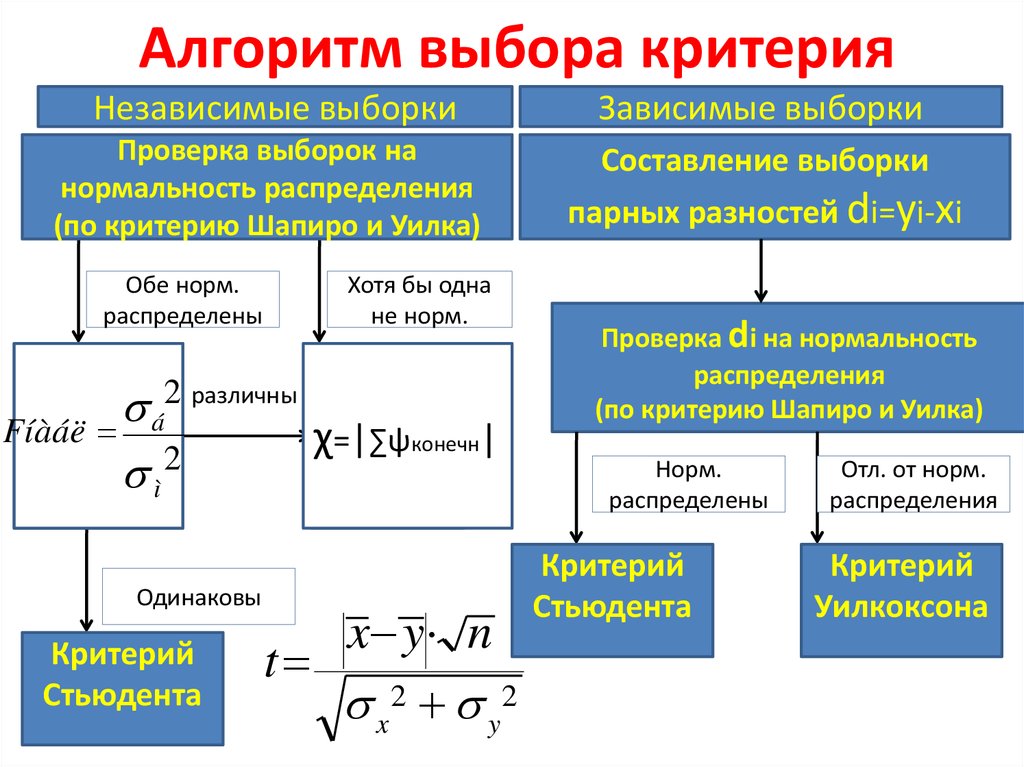
10. Алгоритм выбора критерия

Независимые выборки
Зависимые выборки
Проверка выборок на
нормальность распределения
(по критерию Шапиро и Уилка)
Составление выборки
Обе норм.
распределены
Хотя бы одна
не норм.
Сравнение
их
2 различны
дисперсий
á
Fíàáë
по
критериюì 2
Фишера
Одинаковы
Критерий
Стьюдента
Критерий
- |
=Вандер
|∑ψконечн
Вардена
χ
x y n
t
x 2 y2
парных разностей di=yi-xi
Проверка di на нормальность
распределения
(по критерию Шапиро и Уилка)
Норм.
распределены
Критерий
Стьюдента
Отл. от норм.
распределения
Критерий
Уилкоксона