Жергілікті жердің нүктелер координаталары және олардың аэросуреттегі сол бейнелердің арасындағы байланыс

1.

МАРКШЕЙДЕРЛІК ІС және ГЕОДЕЗИЯ
(кафедрасы)
ФОТОГРАММЕТРИЯ
(пәні)
ТАҚЫРЫБЫ: Жергілікті жердің нүктелер
координаталары және олардың аэросуреттегі
сол бейнелердің арасындағы байланыс.
№_5_ дәріс
Оқытушы
Жантуева Ш.А.

2.

ЛЕКЦИЯ ЖОСПАРЫ
Жергілікті жердің нүктелер координаталары және олардың
аэросуреттегі сол бейнелердің арасындағы байланыс.
1.
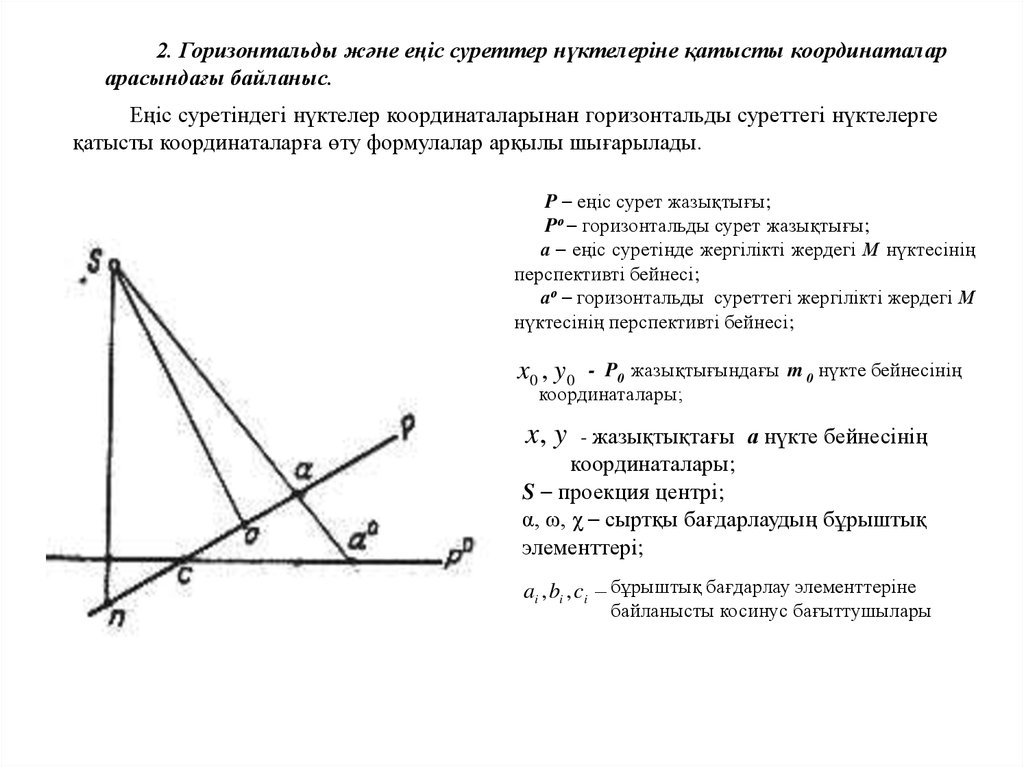
2. Горизонтальды және еңіс суреттер нүктелеріне қатысты
координаталар арасындағы байланыс.

3.

1. Жергілікті жердің нүктелер координаталары және олардың аэросуреттегі сол
бейнелердің арасындағы байланыс.
Суретте жергілікті жердегі N нүктесінен
басталатын, жергілікті жерде қабылданған
NXYZ координаталар жүйесі көрсетілген.
n және N нүктелері сәйкеседі;
М нүктесі NXY жазықтығында болады;
S – проекция центрі;
P – сурет жазықтығы;
m – жергілікті жердегі М нүктесінің сурет
жазықтығындағы
бейнесі.
S нүктесінде
екі координата жүйесі
бар дап есептеледі:
1.
SXYZ
жергілікті
жерде
қабылданған
координата
жүйесіне
параллель;
2. Sx’y’z’, мұнда x’//x; y’//y; z’=z=f.

4.

,
Координаталарды түрлендіруге формулалар қолданылады:
x' a1 x a 2 y a3 f
y ' b1 x b2 y b3 f
- суреттегі m нүкте координаталары,
z ' c1 x c 2 y c3 f
Мұнда
- бағыттауыш косинустар, α, ω, χ, t, α0 , χ. суреттерді бағдарлаудың
бұрыштық элементтеріне тәуелді болады.
Бағыттауыш косинустарды анықтау үшін Sx’y’z’координата жүйесінің үш бұрылуын
орындайдап SXYZжағдайына келтіреді. Ол үшін ось айналасында y’ті ZX
жазықтығында α бұрышына бұрады, ось x’ ті ZY жазықтғында ω бұрышына бұрады ал
z’ ті χ (каппа) бұрышына бұрады.
Мұндай бұруларға матрица сәйкес келеді:
cos
A 0
sin
0
1
A 0 cos
0 sin
0 sin
1
0
0 cos
sin
cos
0
cos
A sin
0
sin
cos
0
0
0
1
- бұрылу матрицасы

5.

Матрицаның туындысын табады:
,
,
sin sin sin cos cos
A
cos sin
cos sin sin sin cos
Әрбір матрицаны
ai , bi , ci
sin sin cos cos sin
sin cos
sin
cos cos
cos cos
cos sin cos sin sin
арқылы белгілейді
b1 cos sin
b2 cos cos
b3 sin
c1 cos sin sin sin cos
c 2 cos sin cos sin sin
c3 cos cos
нәтижесінде аэрофотосуреттерге бағыттауш косинустар алынады.
Егер бағыттауыш косинустар белгілі болса, онда α, ω, χ бұрыштарын формула бойынша
табуға болады:
a3
tg
c3
tg b3
'
Sx’y’z’ координата жүйесіндегі m нүктесі R1
tg
b1
b2
вектормен
x' x
координаталар
y ' y z ' f ымен
анықталады.

6.

SXYZ координата жүйесінде - R1
R1' және R1
сол вектормен X’Y’Z’ координаталарымен анықталады.
векторлары коллинеарлы болғандықтан R R болады.
1
-
ол коэффициент.
Бұл векторлардың компоненттері пропорционалды болғандықтан мына түрде жазылады:
X ' Y' Z'
X
Y
Z
Z H болғандықтан
a x a 2 y a3 f
X'
X Z ' H 1
c1 x c 2 y c3 f
Z
b x b2 y b3 f
Y'
Y Z H 1
Z'
c1 x c 2 y c3 f
x0
HA
f
y
0 HA
f
еңіс суреттерге
XA
YA
горизонтальды суреттерге

7.

Мұндай теңдеулерді жергілікті жердің әр бір нүктесіне құруға болады, егерде
суреттегі нүктенің үш белгісіздердің x, y, z бағдарлау элементтері белгілі болса.
x f
a1 x b1 y c1 z
a3 x b3 y c3 z
y f
a 2 x b2 y c 2 z
a3 x b3 y c3 z
Суреттегі нүкте координаталары мен жергілікті жердегі нүкте
координаталары арасындағы байланыс қатынастан алынады:
x' y ' z '
x y z

8.

2. Горизонтальды және еңіс суреттер нүктелеріне қатысты координаталар
арасындағы байланыс.
Еңіс суретіндегі нүктелер координаталарынан горизонтальды суреттегі нүктелерге
қатысты координаталарға өту формулалар арқылы шығарылады.
P – еңіс сурет жазықтығы;
Pо – горизонтальды сурет жазықтығы;
а – еңіс суретінде жергілікті жердегі М нүктесінің
перспективті бейнесі;
ао – горизонтальды суреттегі жергілікті жердегі М
нүктесінің перспективті бейнесі;
- P0 жазықтығындағы m 0 нүкте бейнесінің
координаталары;
x0 , y 0
x, y
- жазықтықтағы а нүкте бейнесінің
координаталары;
S – проекция центрі;
α, ω, χ – сыртқы бағдарлаудың бұрыштық
элементтері;
ai , bi , ci бұрыштық бағдарлау элементтеріне
байланысты косинус бағыттушылары

9.

Егер
a1 b2 c3
= 1,
a2 a3 b1 b3 c1 c3 0
0
жергілікті жердегі нүкте координаталары мен олардың суреттегі бейнелерінің
координаталары байланыстарының формуласын есептеп суретте жергілікті жердің М
нүктесінің координаталарын алуға болады.
X M H M
YM H M
a1 x a 2 y a3 f
c1 x c 2 y c3 f
b1 x b2 y b3 f
c1 x c 2 y c3 f
x0
HM
f
y
YM 0 H M
f
- еңіс суреттерге
XM
- горизонталь суреттерге

10.

Теңдеулерді оң жақ бөлікке теңестіріп
x0 , y 0
мағынасын алуға болады:
x0 f
a1 x a 2 y a3 f
c1 x c2 y c3 f
y0 f
b1 x b2 y b3 f
c1 x c2 y c3 f
Шыққан формулаларды еңіс суреттен горизонтальдыға өтуде қолданылады
яғни сыртқы бағдарлау элементтерінің шарттары мен проекция центрінің жағдайын
сақтай отырып еңіс суретіндегі нүкте координаталарын горизонтальдыға
трансформациялауда қолданады.

11.

БАҚЫЛАУ СҰРАҚТАРЫ
1. Косинус бағыттаушыларын анықтау үшін неше координата
жүйесінің бұрылысын орындау қажет?
2. α, ω, χ бұрыштарын формула бойынша табу үшін қандай
шамалар белгілі болуы керек?
3. деген не?
4. Шығарылған формулалар қандай мақсатта қолданылады?
5. Бағыттауыш косинустар неге бпйланысты болады?