Похожие презентации:
Гипербола. Кривая второго порядка
1. Гипербола
Кривая второго порядка2. Определение гиперболы
Гипербола — это плоская кривая второго порядка,которая состоит из двух отдельных кривых, которые
не пересекаются.
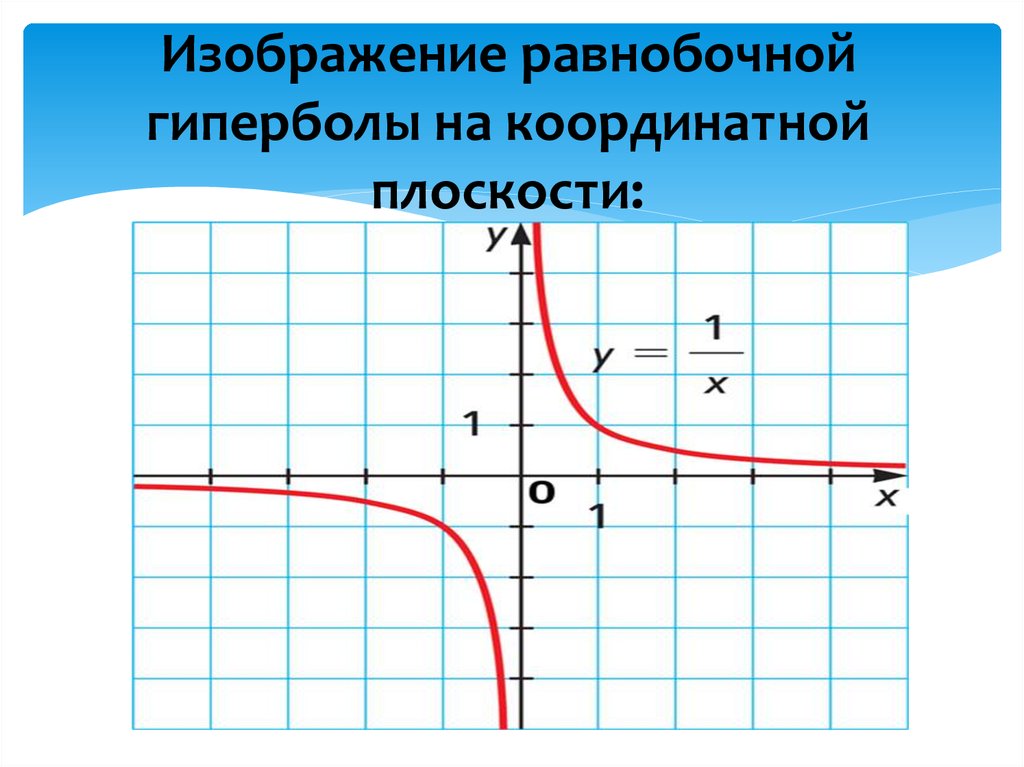
Формула гиперболы y = k/x, при условии, что k не
равно 0. То есть вершины гиперболы стремятся к
нолю, но никогда не пересекаются с ним.
Гипербола — это множество точек плоскости, модуль
разности расстояний которых от двух точек,
называемых фокусами, есть величина постоянная.
3. Свойства гиперболы
Оптическое свойство: свет от источника, находящегося водном из фокусов гиперболы, отражается второй ветвью
гиперболы таким образом, что продолжения отраженных
лучей пересекаются во втором фокусе.
Иначе говоря, если F1 и F2 фокусы гиперболы, то
касательная в любой точки X гиперболы является
биссектрисой угла ∠F1XF2.
Для любой точки, лежащей на гиперболе, отношение
расстояний от этой точки до фокуса к расстоянию от этой
же точки до директрисы есть величина постоянная.
4. Свойства гиперболы (Продолжение)
Гипербола обладает зеркальной симметриейотносительно действительной и мнимой осей, а
также вращательной симметрией при повороте на угол
180° вокруг центра гиперболы.
Каждая гипербола имеет сопряженную гиперболу, для
которой действительная и мнимая оси меняются местами,
но асимптоты остаются прежними.
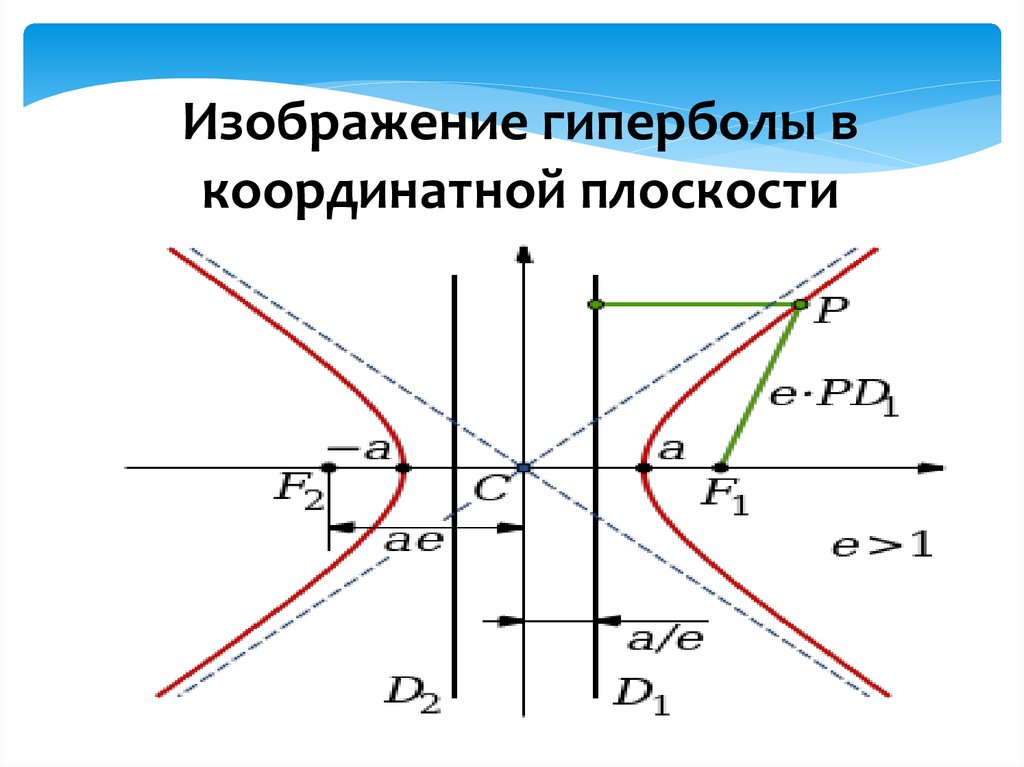
5. Изображение гиперболы в координатной плоскости
6. Обозначения:
Асимптоты гиперболы (красные кривые) , показанные голубымпунктиром, пересекаются в центре гиперболы, C.
Два фокуса гиперболы обозначены как F1 и F2.
Директрисы гиперболы обозначены линиями двойной толщины и
обозначены D1 и D2.
Эксцентриситет e равен отношению расстояний точки P на
гиперболе до фокуса и до соответствующей директрисы
(показаны зелёным).
Вершины гиперболы обозначены как ±a.
Параметры гиперболы обозначают следующее:
a — расстояние от центра C до каждой из вершин
b — длина перпендикуляра к оси абсцисс, восставленного из
каждой из вершин до пересечения с асимптотой
c — расстояние от центра C до любого из фокусов,F1 и F2,
θ — угол, образованный каждой из асимптот и осью, проведённой
между вершинами
7. Эксцентриситет гиперболы
Эксцентриситетом гиперболы называется величинаe , равная отношению c/a, где:
c=




















 Математика
Математика








