Похожие презентации:
Электронные таблицы
1. Электронные таблицы
2. Определение и назначение
Электронная таблица – это работающее в диалоговом режимеприложение, хранящее и обрабатывающее данные в
прямоугольных таблицах.
Основная задача – автоматические вычисления с данными в
таблицах.
Кроме того:
• хранение данных в табличном виде
• представление данных в виде диаграмм
• анализ данных
• составление прогнозов
• поиск оптимальных решений
• подготовка и печать отчетов
3. Microsoft® Office Excel® 2007
4. Интерфейс
Практически все команды видны яснее и доступныблагодаря единому центральному элементу управления
под простым названием — лента.
5. Интерфейс
Лента состоит из трех элементов: вкладок, групп и команд.1 Вкладки: Вкладки предоставляют возможность выполнять основные задачи,
предусмотренные в Excel. В верхней части окна Excel доступно семь вкладок.
2 Группы:
Группы являются
отображаются на вкладках.
наборами
связанных
команд,
которые
3 Команды: Командой может быть кнопка, меню или поле, предназначенное
для ввода сведений.
6. Интерфейс
Чтобы все имеющиеся команды не отображалисьодновременно, в Excel 2007 некоторые из них
отображаются только в ответ на конкретное действие
пользователя, когда в них возникает необходимость.
7. Интерфейс
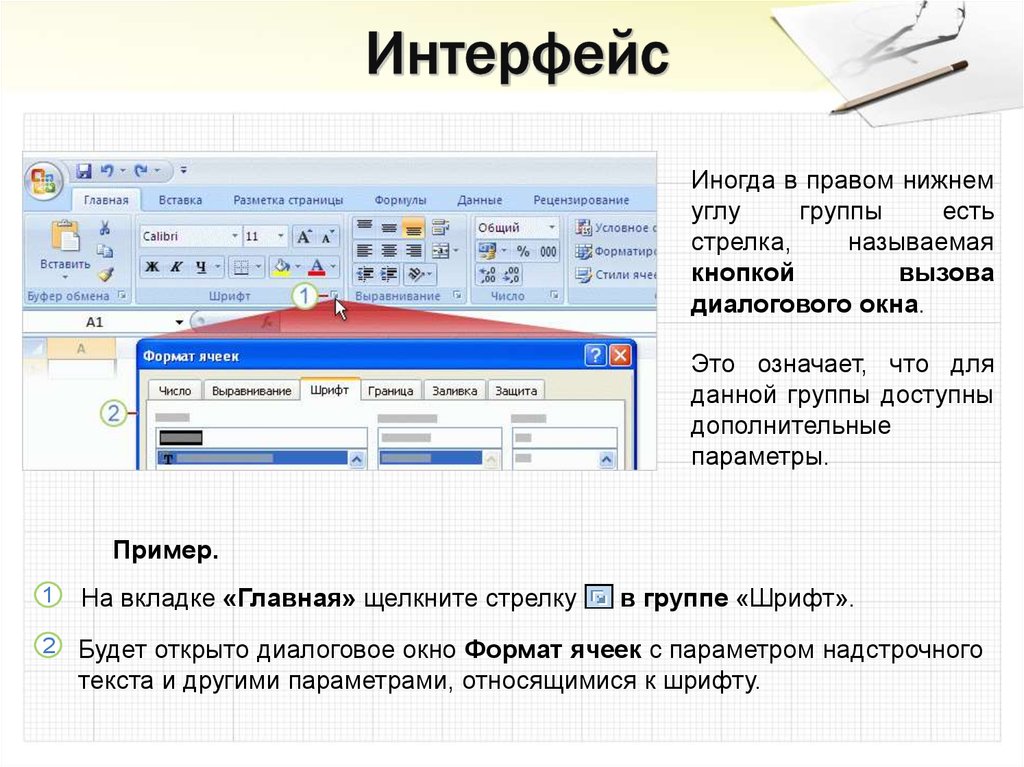
Иногда в правом нижнемуглу
группы
есть
стрелка,
называемая
кнопкой
вызова
диалогового окна.
Это означает, что для
данной группы доступны
дополнительные
параметры.
Пример.
1
На вкладке «Главная» щелкните стрелку
в группе «Шрифт».
2
Будет открыто диалоговое окно Формат ячеек с параметром надстрочного
текста и другими параметрами, относящимися к шрифту.
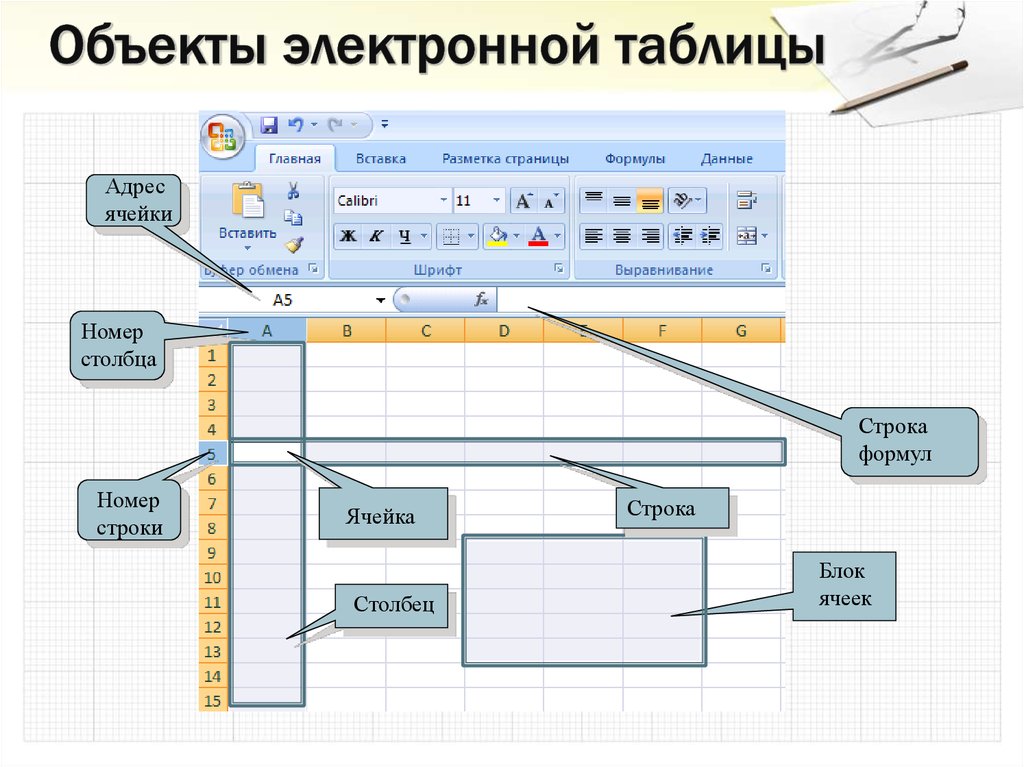
8. Объекты электронной таблицы
Адресячейки
Номер
столбца
Строка
формул
Номер
строки
Ячейка
Столбец
Строка
Блок
ячеек
9. Основные понятия электронных таблиц
Ячейка – элементарный объект электроннойрасположенный на пересечении столбца и строки.
таблицы,
Строка – все ячейки, расположенные на одном горизонтальном
уровне.
Столбец – все ячейки, расположенные в одном вертикальном
ряду таблицы.
Диапазон ячеек – группа смежных ячеек, которая может
состоять из одной ячейки, строки (или ее части), столбца (или
его части), а также из совокупности ячеек, охватывающих
прямоугольную область таблицы.
При работе на компьютере электронная таблица существует в
форме рабочего листа, который имеет имя(например, Лист1).
Рабочие листы объединяются в книги.
10. Имена объектов электронной таблицы
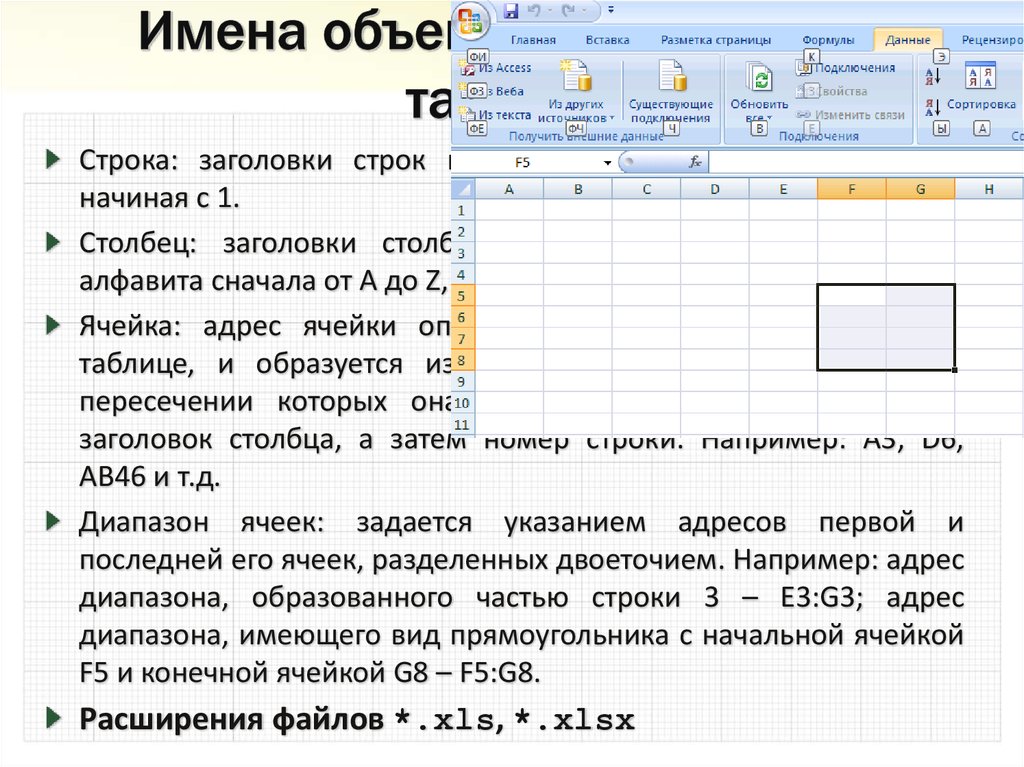
Строка: заголовки строк представлены в виде целых чисел,начиная с 1.
Столбец: заголовки столбцов задаются буквами латинского
алфавита сначала от A до Z, затем от АА до AZ, от ВА до ВZ и т.д.
Ячейка: адрес ячейки определяется ее местоположением в
таблице, и образуется из заголовков столбца и строки, на
пересечении которых она находится. Сначала записывается
заголовок столбца, а затем номер строки. Например: А3, D6,
АВ46 и т.д.
Диапазон ячеек: задается указанием адресов первой и
последней его ячеек, разделенных двоеточием. Например: адрес
диапазона, образованного частью строки 3 – Е3:G3; адрес
диапазона, имеющего вид прямоугольника с начальной ячейкой
F5 и конечной ячейкой G8 – F5:G8.
Расширения файлов *.xls, *.xlsx
11. Типы данных
Текстовый тип данныхТекстовые данные представляют собой некоторый набор
символов. Если первый из них является буквой, кавычкой,
апострофом или пробелом, либо цифры чередуются с буквами,
то такая запись воспринимается как текст.
Действия над текстовыми данными производятся аналогично
действиям над объектами в текстовом процессоре.
Пример текстовых данных:
Расписание занятий
8 «А» класс
‘’236
001 счет
12. Типы данных
Числовой тип данныхЧисловые данные представляют собой последовательность
цифр, которые могут быть разделены десятичной запятой и
начинаться с цифры, знака числа (+ или -), или десятичной
запятой.
Над числовыми данными в электронной таблице могут
производиться различные математические операции.
Пример числовых данных:
232,5
-13,7
+100
,345
13.
Внешний признак, по которому можно различитьтекстовые и числовые данные:
Если в ячейку вводится текст, то после нажатия клавиши
<Entеr> он автоматически (по умолчанию) выравнивается по
левой границе ячейки. В противоположность этому числовые
данные при вводе выравниваются по правой границе ячейки:
13
14. Тип данных
– датыЭтот тип данных используется при выполнении таких функций,
как добавление к дате числа, получение разности двух дат, при
пересчете даты. Например вперед или назад. Пересчет чисел в
даты производится автоматически в зависимости от заданного
формата. Табличный процессор позволяет представлять
вводимые числа как даты несколькими способами.
Пример. Представление дат в разных форматах:
4 июня 1989
06.98
Июнь 2001
4 июня
04.06.
Июнь
15. Формат данных
Процентный формат данныхПроцентный формат обеспечивает представление числовых
данных в форме процентов со знаком %.
Например, если установлена точность в один десятичный знак,
то при вводе числа 0.257 на экране появится 25.7%, а при вводе
числа 257 на экране появится 25700.0%.
Денежный формат
Денежный формат обеспечивает такое представление чисел,
при котором каждые три разряда разделены пробелом, а
следом за последним десятичным знаком указывается
денежная единица размерности – «р» (рубли). Например,
число 12345 будет записано в ячейке как 12345 р.
16.
арифметическая прогрессиякопирование формул
маркер
заполнения
ЛКМ
даты
ЛКМ
время
списки
16
17.
размервсе свойства
направление
в несколько
строк
денежный
формат
количество знаков
в дробной части
17
18. Понятие формулы
Формула–
математическое
выражение,
записанное по правилам, установленным в
среде табличного процессора.
Ввод формулы начинается со знака равенства.
Если его пропустить, то вводимая формула будет
воспринята как текст. В формулы могут
включаться числовые данные, адреса объектов
таблицы, а также различные функции.
Различают арифметические (алгебраические) и
логические формулы.
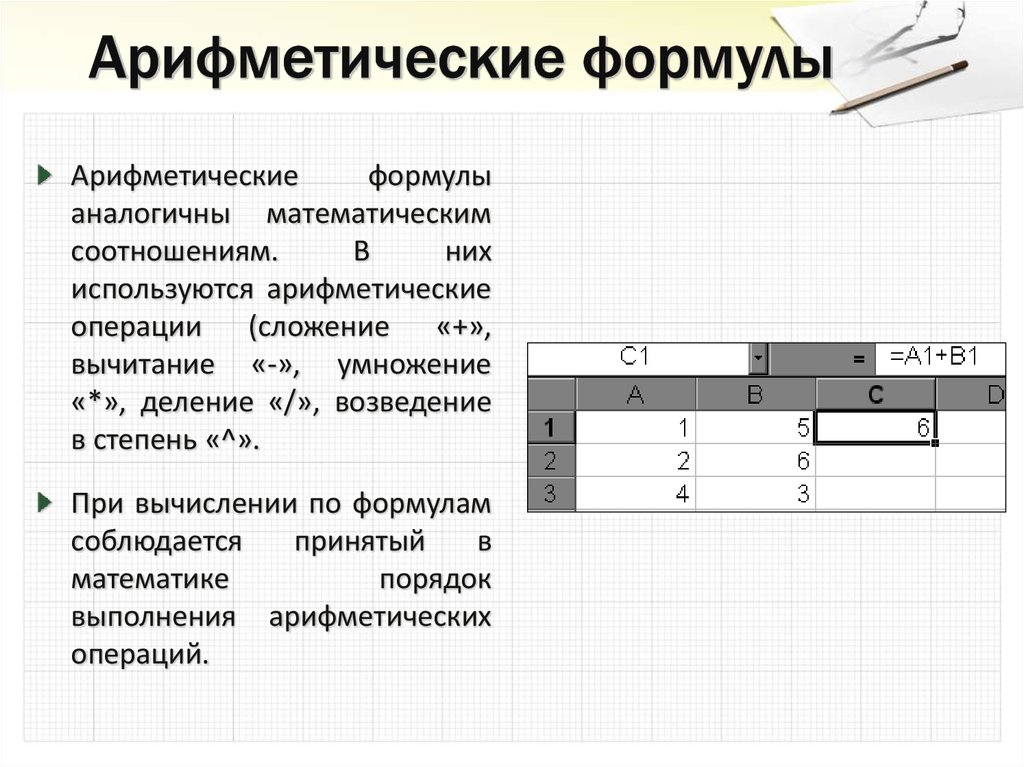
19. Арифметические формулы
аналогичны математическимсоотношениям.
В
них
используются арифметические
операции (сложение «+»,
вычитание «-», умножение
«*», деление «/», возведение
в степень «^».
При вычислении по формулам
соблюдается
принятый
в
математике
порядок
выполнения арифметических
операций.
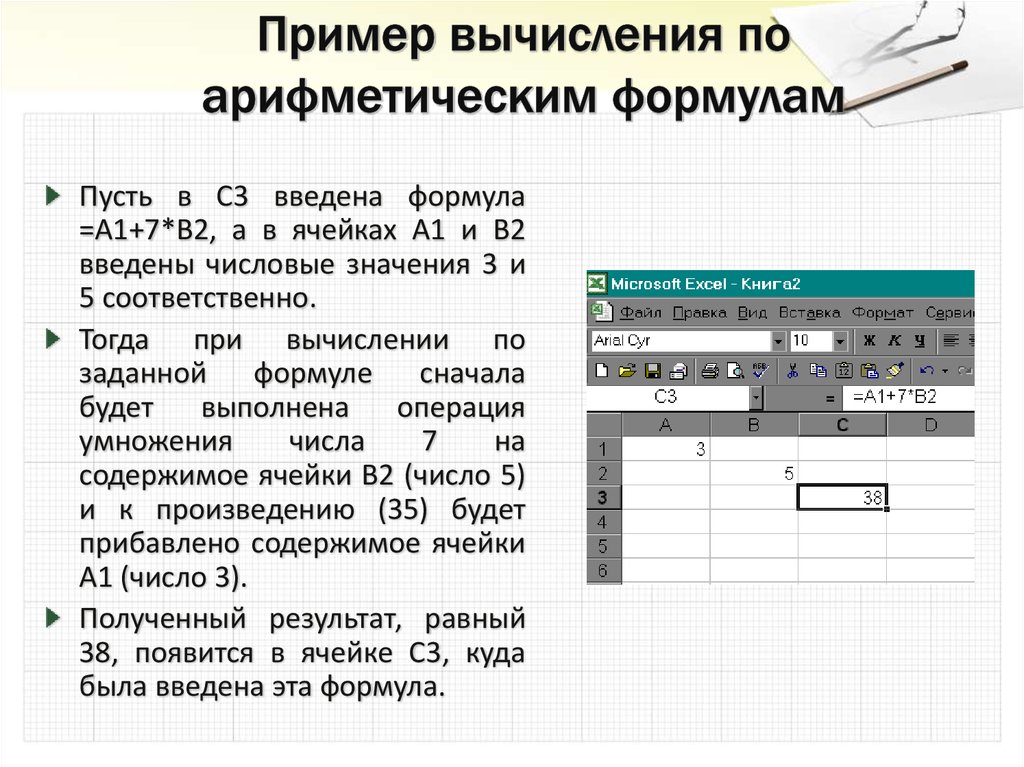
20. Пример вычисления по арифметическим формулам
Пусть в С3 введена формула=А1+7*В2, а в ячейках А1 и В2
введены числовые значения 3 и
5 соответственно.
Тогда при вычислении по
заданной формуле
сначала
будет
выполнена
операция
умножения
числа
7
на
содержимое ячейки В2 (число 5)
и к произведению (35) будет
прибавлено содержимое ячейки
А1 (число 3).
Полученный результат, равный
38, появится в ячейке С3, куда
была введена эта формула.
21. Ответьте на вопросы
Какой результат будет получен в ячейках с формулами?1
2
3
4
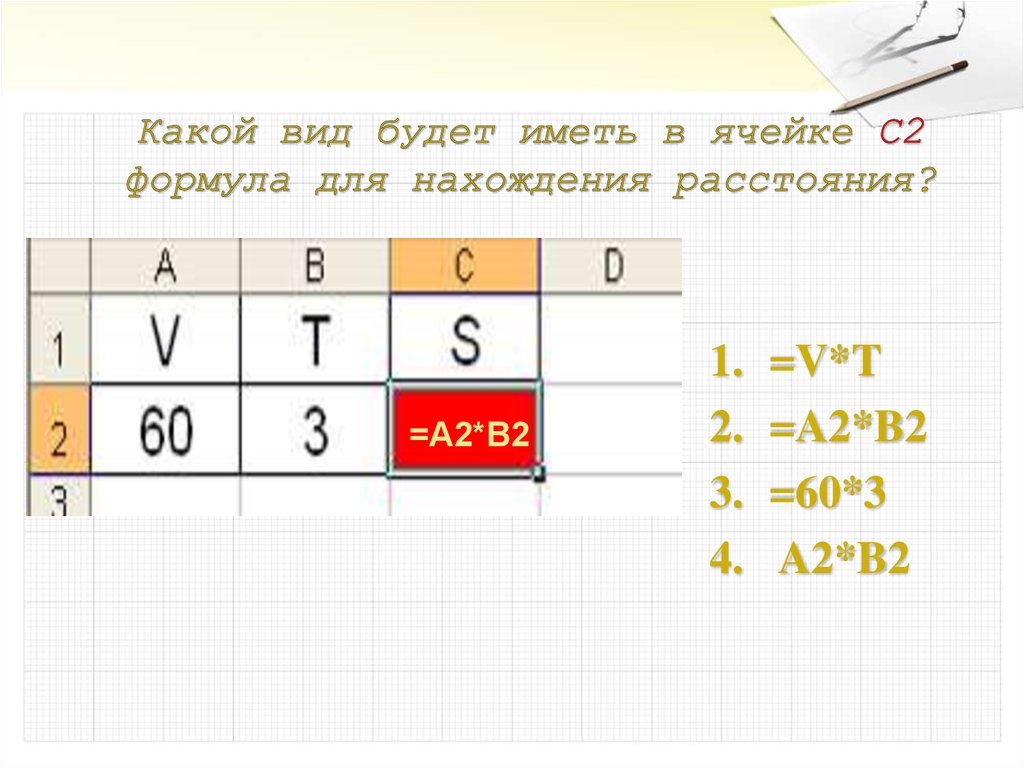
22. Какой вид будет иметь в ячейке С2 формула для нахождения расстояния?
=A2*B21.
2.
3.
4.
=V*T
=A2*B2
=60*3
A2*B2
23. Относительные, абсолютные и смешанные ссылки
24. Понятие ссылки
Адреса, которые используются в формулах, получили названиессылок. Ссылки позволяют связывать между собой любые
ячейки электронной таблицы и проводить необходимую
обработку табличных данных.
Ссылка — адрес объекта (ячейки, строки, столбца, диапазона),
используемый при записи формулы.
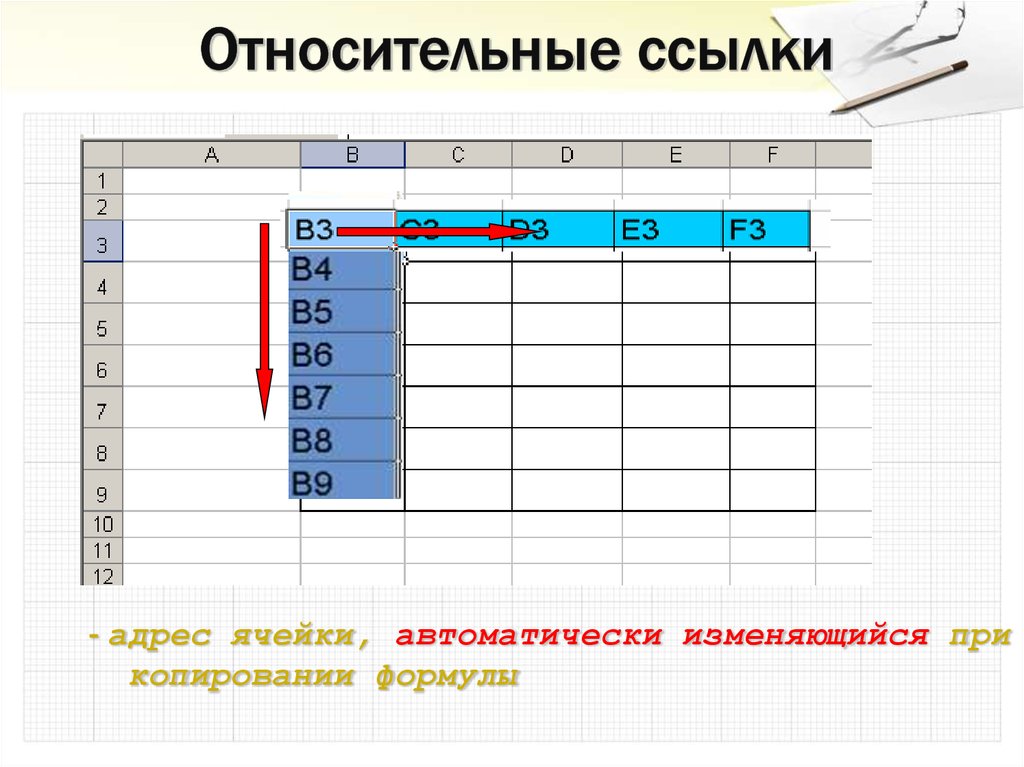
25.
- адрес ячейки, автоматически изменяющийся прикопировании формулы
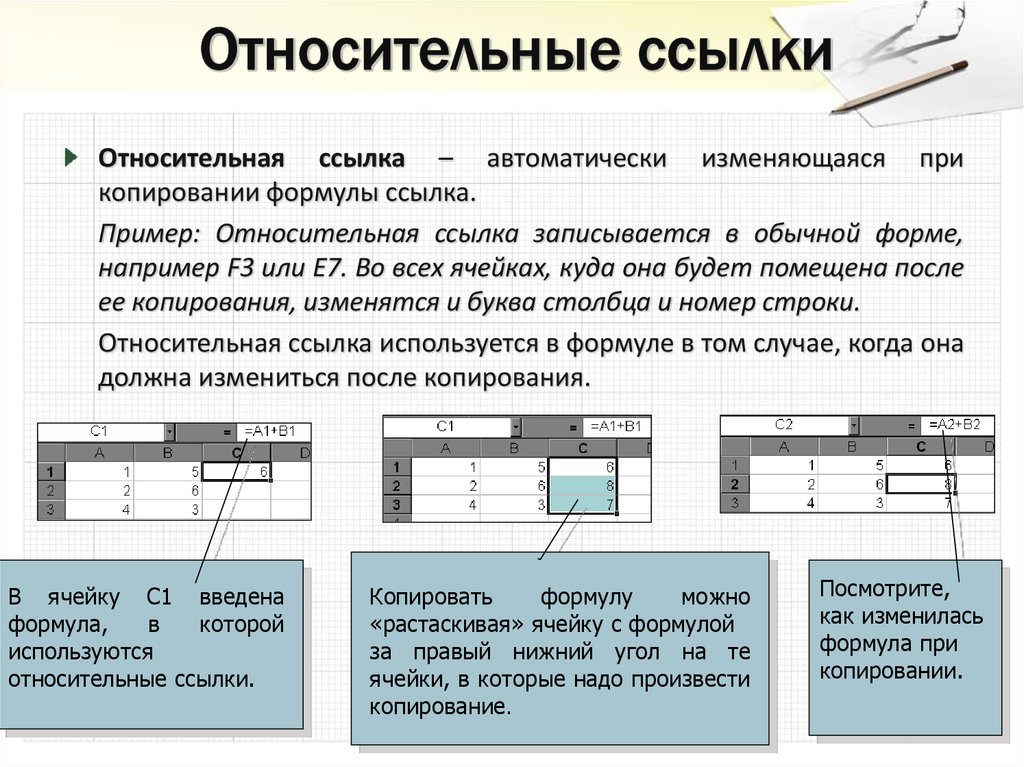
26. Относительные ссылки
Относительная ссылка – автоматически изменяющаяся прикопировании формулы ссылка.
Пример: Относительная ссылка записывается в обычной форме,
например F3 или E7. Во всех ячейках, куда она будет помещена после
ее копирования, изменятся и буква столбца и номер строки.
Относительная ссылка используется в формуле в том случае, когда она
должна измениться после копирования.
В ячейку С1 введена
формула,
в
которой
используются
относительные ссылки.
Копировать
формулу
можно
«растаскивая» ячейку с формулой
за правый нижний угол на те
ячейки, в которые надо произвести
копирование.
Посмотрите,
как изменилась
формула при
копировании.
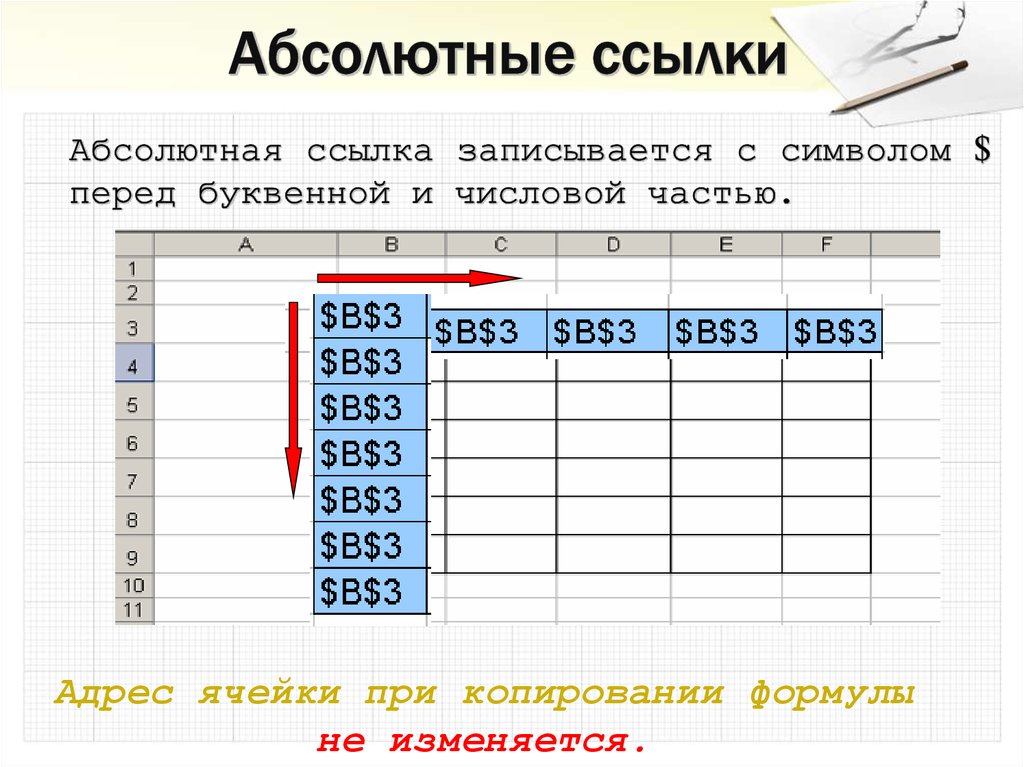
27. Абсолютная ссылка записывается с символом $ перед буквенной и числовой частью.
Адрес ячейки при копировании формулыне изменяется.
28. Абсолютные ссылки
Абсолютная ссылка – не изменяющаяся при копировании формулыссылка.
Абсолютная ссылка записывается в формуле в том случае, если при
ее копировании не должны изменяться обе части: буква столбца и
номер строки. Это указывается с помощью символа $, который
ставится и перед буквой столбца и перед номером строки.
Пример: Абсолютная ссылка: $А$6. При копировании формулы
=4+$A$6 во всех ячейках, куда она будет скопирована, появятся
точно такие же формулы.
В формуле используются
абсолютные ссылки
Обратите
внимание,
что
при
копировании формулы на другие
ячейки, сама формула не изменятся.
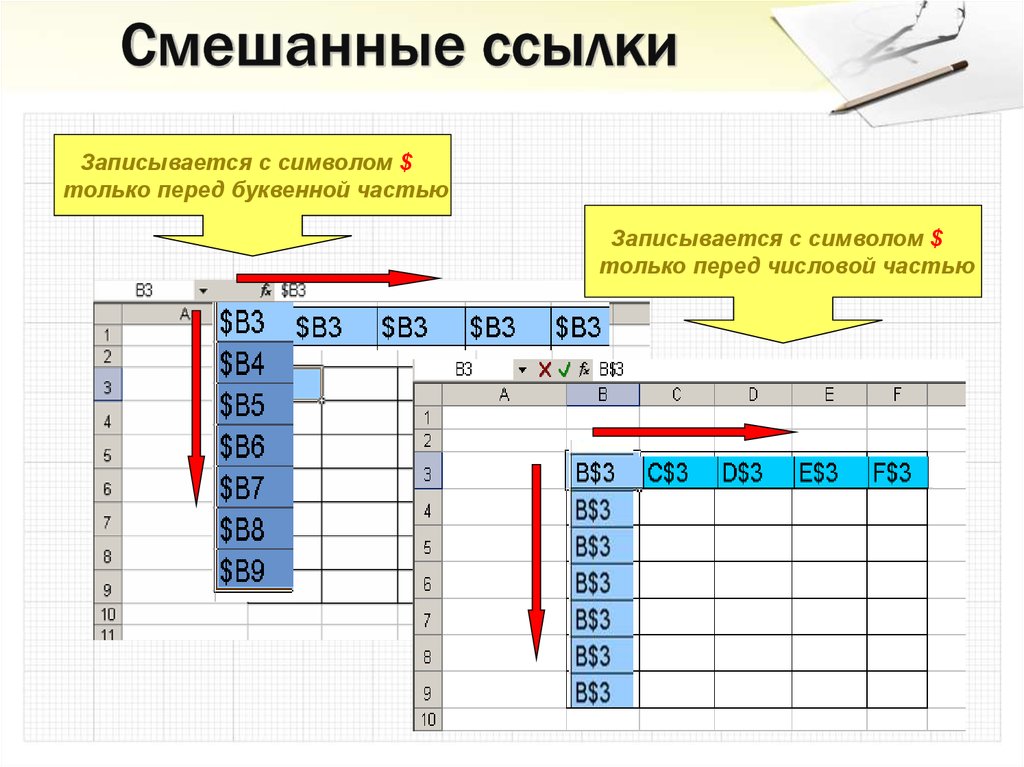
29. Смешанные ссылки
Записывается с символом $только перед буквенной частью
Записывается с символом $
только перед числовой частью
30. Смешанные ссылки
Смешанная ссылка используется, когда при копированииформулы может изменяться только какая-то одна часть ссылки
– либо буква столбца, либо номер строки. При этом символ $
ставится перед той частью ссылки, которая должна остаться
неизменной.
Пример: Смешанные ссылки с неизменяемой буквой столбца:
$C8, $F12; смешанные ссылки с неизменяемым номером
строки: A$5, F$9.
31. Функции
32. Назначение функций
Функциями называют встроенные в Excel формулы.Функции позволяют производить сложные вычисления в
электронных таблицах.
В Excel имеется несколько видов встроенных функций:
Математические;
Статистические;
Дата и время;
Логические и другие.
Функции можно использовать как по отдельности, так и в сочетании с
другими функциями и формулами;
После имени каждой функции в ( ) задаются аргументы. Если функция
не использует аргументы, то за её именем следуют пустые ( ) без
пробела между ними;
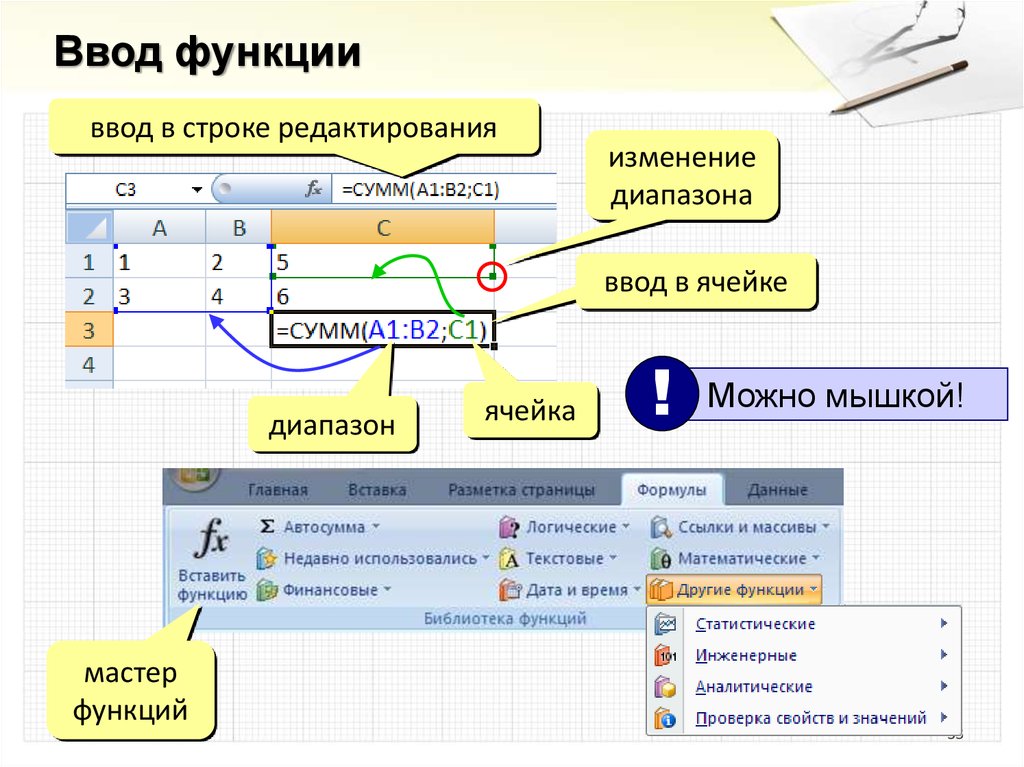
33.
Ввод функцииввод в строке редактирования
изменение
диапазона
ввод в ячейке
диапазон
мастер
функций
ячейка
!
Можно мышкой!
33
34. МАТЕМАТИЧЕСКИЕ функции
Вид записиНазначение
КОРЕНЬ(…) Вычисление квадратного корня
ABS(…)
Вычисление абсолютного значения(модуля) числа
ЦЕЛОЕ(…)
Округление числа или результата выражения, указанного
в скобках до ближайшего целого числа
ПИ()
Значение математической константы «ПИ» (3,1415926…)
НОД(…)
Наибольший общий делитель нескольких чисел
СЛЧИС()
Вычисление случайного числа в промежутке
между 0 и 1
35. СТАТИСТИЧЕСКИЕ функции
Вид записиНазначение
МИН(…)
Определение минимального из указанных чисел
МАКС(…)
Определение максимального из указанных чисел
СРЕДНЕЕ(…) Определение среднего значения указанных чисел
СУММ(…)
Определение суммы указанных чисел
36. Функции ДАТА И ВРЕМЯ
Вид записиНазначение
СЕГОДНЯ()
Значение сегодняшней даты в виде даты в числовом
формате
МЕСЯЦ(дата)
Вычисление порядкового номера месяца в году по
указанной дате
ДЕНЬ(дата)
Вычисление порядкового номера дня в месяце по
указанной дате
ГОД(дата)
Вычисление года по указанной дате
37. Логические функции
И(условие1;условие2;…) – вычисляет значения(ИСТИНА, ЛОЖЬ) логической операции «И»
ИЛИ(условие1;условие2;…) - вычисляет значения
(ИСТИНА, ЛОЖЬ) логической операции «И»
ЕСЛИ(условие; знач_Истина; знач_Ложь) –
вычисляет значения в зависимости от выполнения
условия
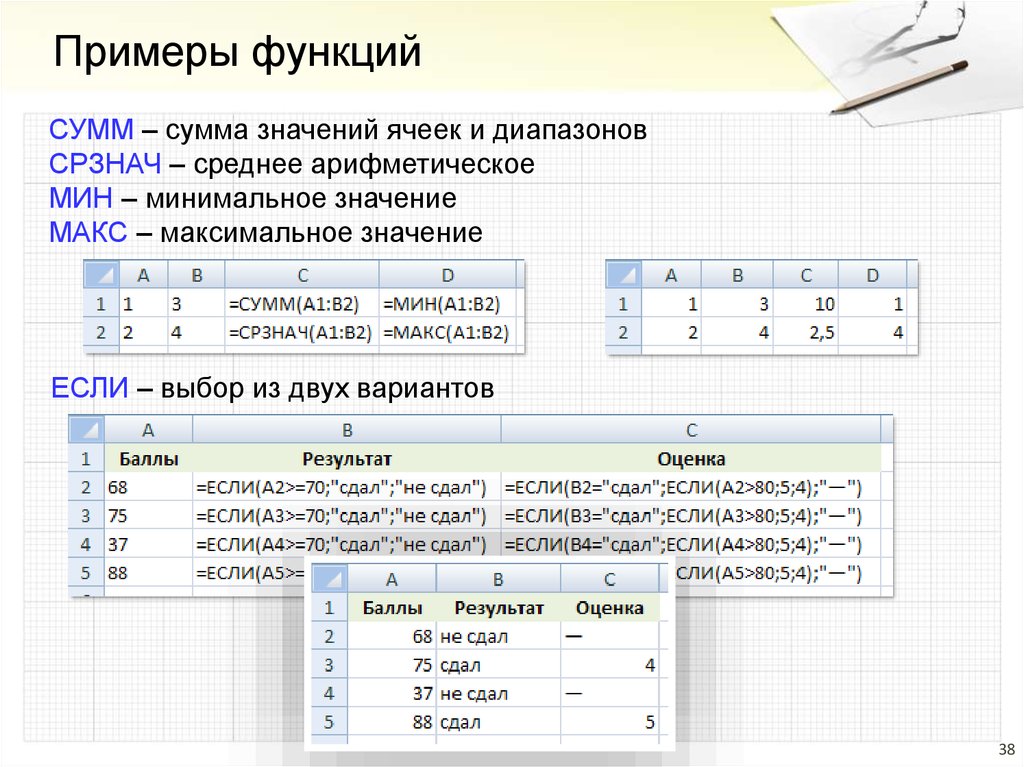
38.
Примеры функцийСУММ – сумма значений ячеек и диапазонов
СРЗНАЧ – среднее арифметическое
МИН – минимальное значение
МАКС – максимальное значение
ЕСЛИ – выбор из двух вариантов
38
39.
Примеры функцийЕСЛИ – выбор из двух вариантов
НЕ – обратное условие, НЕ(B2<10) B2>=10
?
И – одновременное выполнение всех условий
ИЛИ – выполнение хотя бы
одного из условий
39
40.
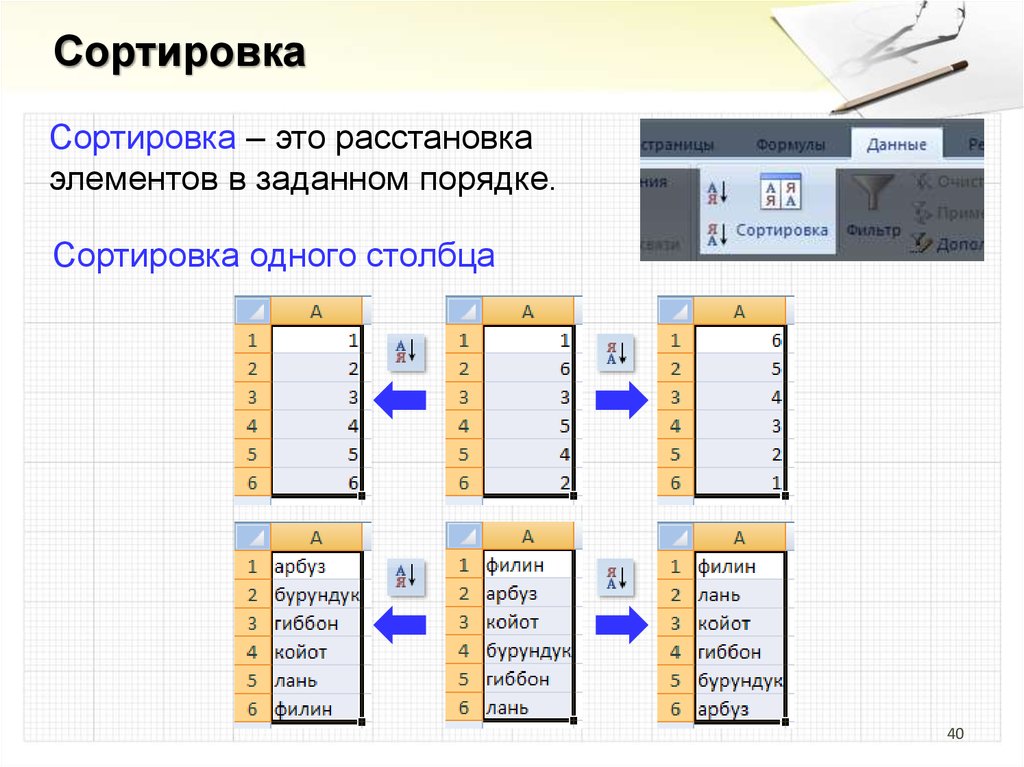
СортировкаСортировка – это расстановка
элементов в заданном порядке.
Сортировка одного столбца
40
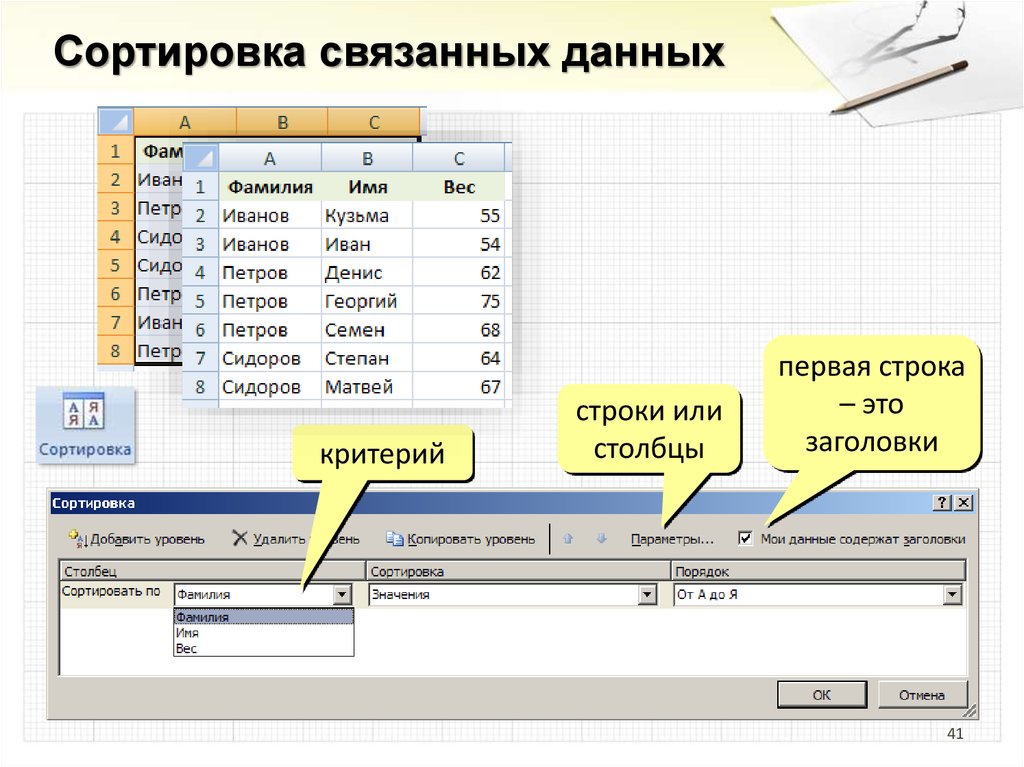
41.
Сортировка связанных данныхкритерий
строки или
столбцы
первая строка
– это
заголовки
41
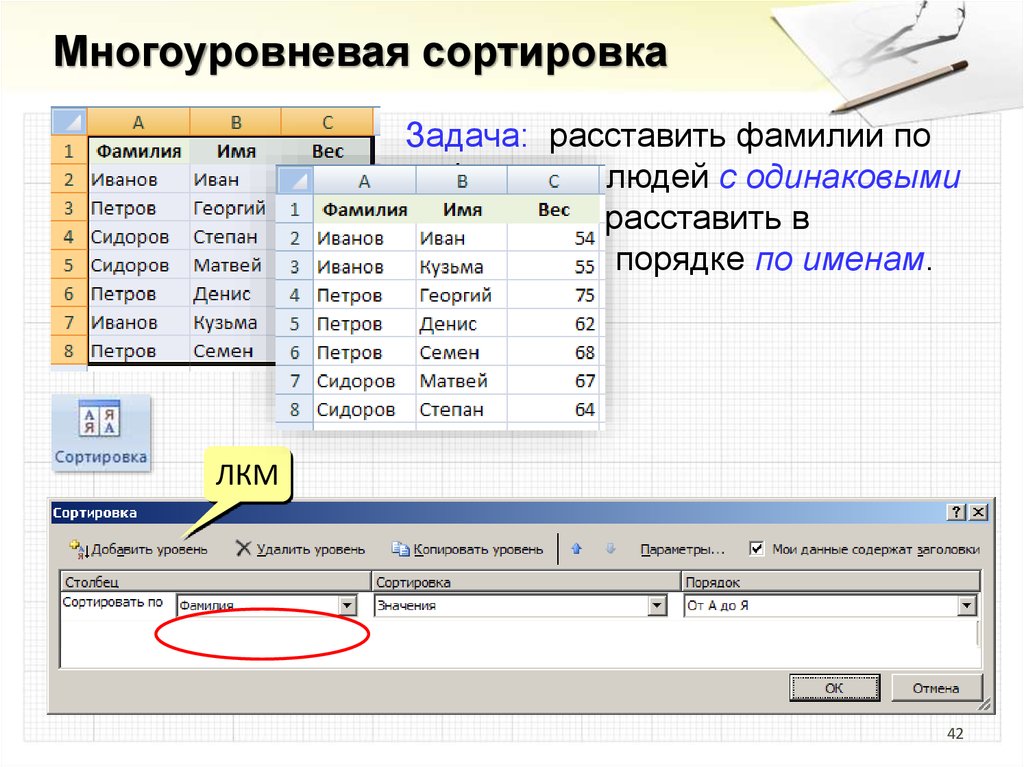
42.
Многоуровневая сортировкаЗадача: расставить фамилии по
алфавиту, а людей с одинаковыми
фамилиями расставить в
алфавитном порядке по именам.
ЛКМ
42
43. Диаграммы
44. Понятие диаграммы
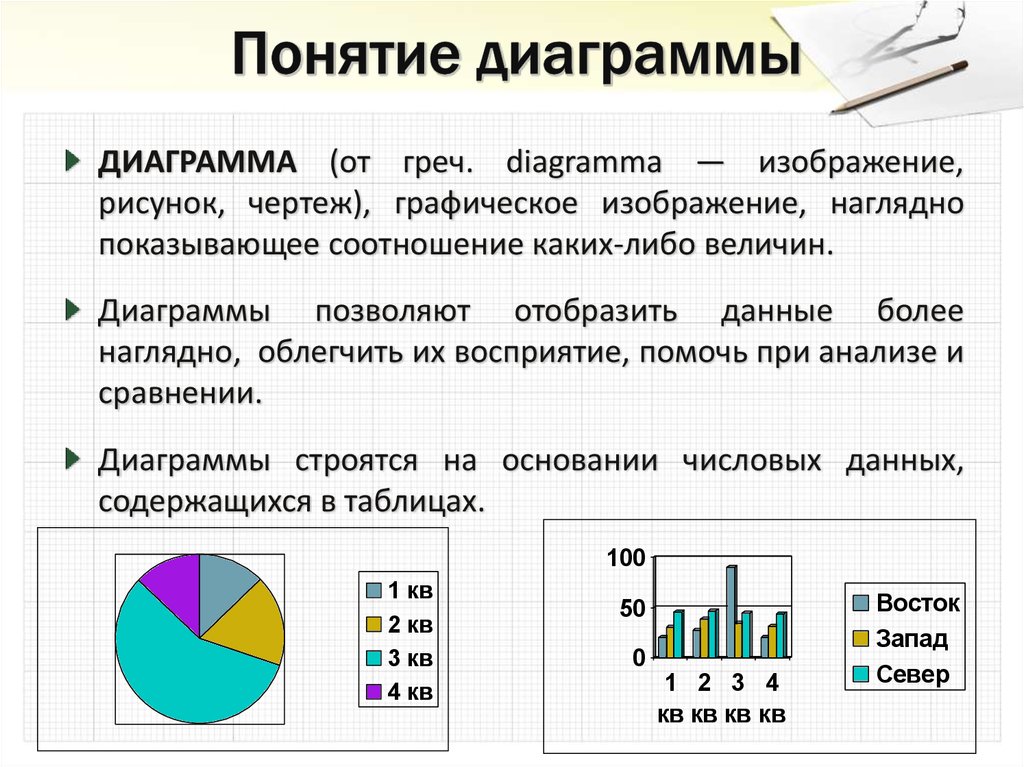
ДИАГРАММА (от греч. diagramma — изображение,рисунок, чертеж), графическое изображение, наглядно
показывающее соотношение каких-либо величин.
Диаграммы позволяют отобразить данные более
наглядно, облегчить их восприятие, помочь при анализе и
сравнении.
Диаграммы строятся на основании числовых данных,
содержащихся в таблицах.
100
1 кв
2 кв
3 кв
4 кв
50
0
1 2 3 4
кв кв кв кв
Восток
Запад
Север
45.
Общий подход к построению• диаграммы строятся на основе данных таблицы
• проще всего сначала выделить все нужные данные, а
потом…
• все данные, которые должны обновляться
автоматически, нужно выделить
• для выделения несвязанных диапазонов используем
+Ctrl
45
46.
Основные типы диаграммГистограмма (столбчатая диаграмма):
сравнение значений одного или
нескольких рядов данных
График: показывает изменение
процесса во времени (равномерные
отсчеты)
Круговая: доли в сумме
Точечная: связь между
парами значений (график функции)
46
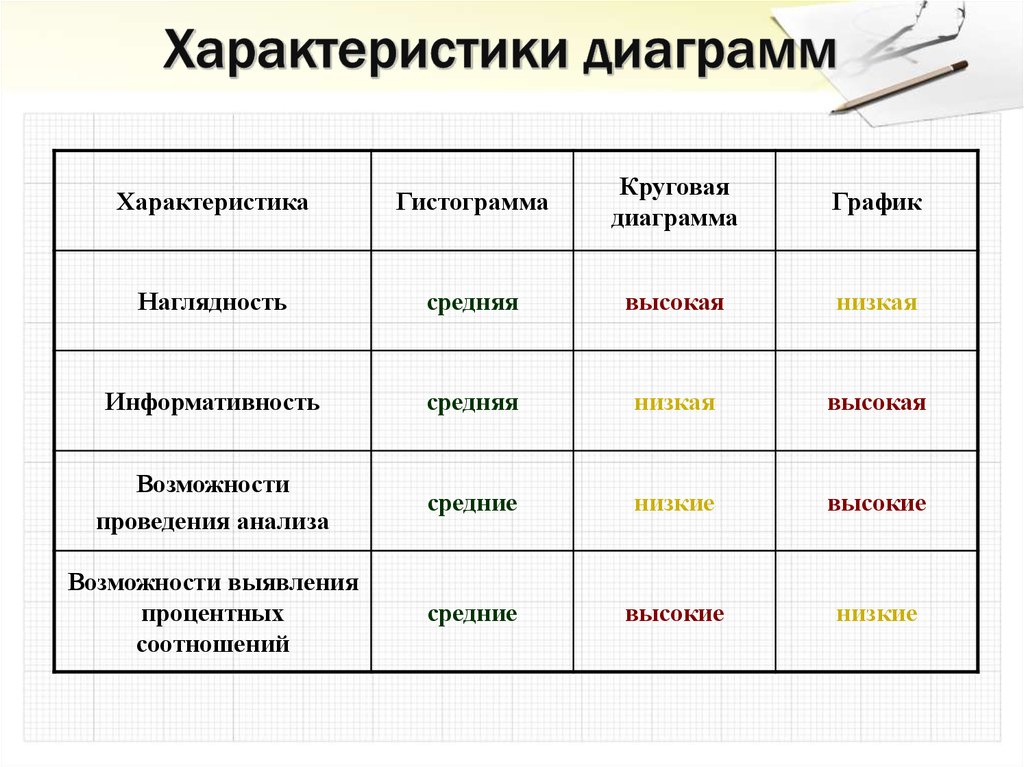
47. Характеристики диаграмм
ХарактеристикаГистограмма
Круговая
диаграмма
График
Наглядность
средняя
высокая
низкая
Информативность
средняя
низкая
высокая
Возможности
проведения анализа
средние
низкие
высокие
Возможности выявления
процентных
соотношений
средние
высокие
низкие
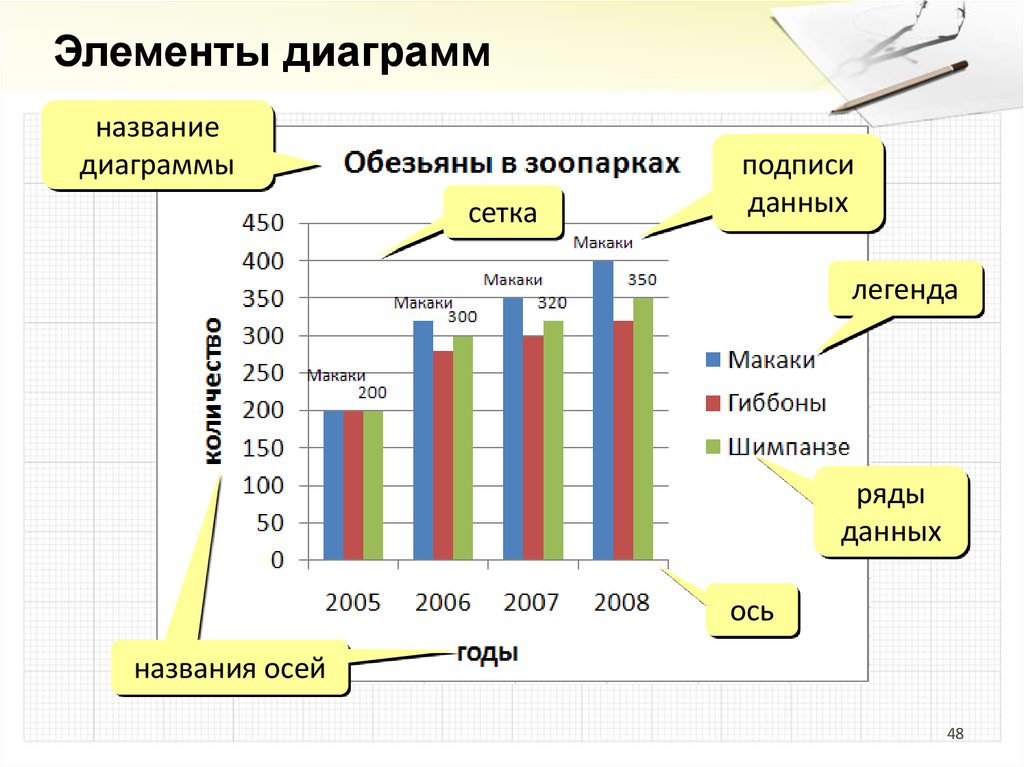
48.
Элементы диаграммназвание
диаграммы
сетка
подписи
данных
легенда
ряды
данных
ось
названия осей
48
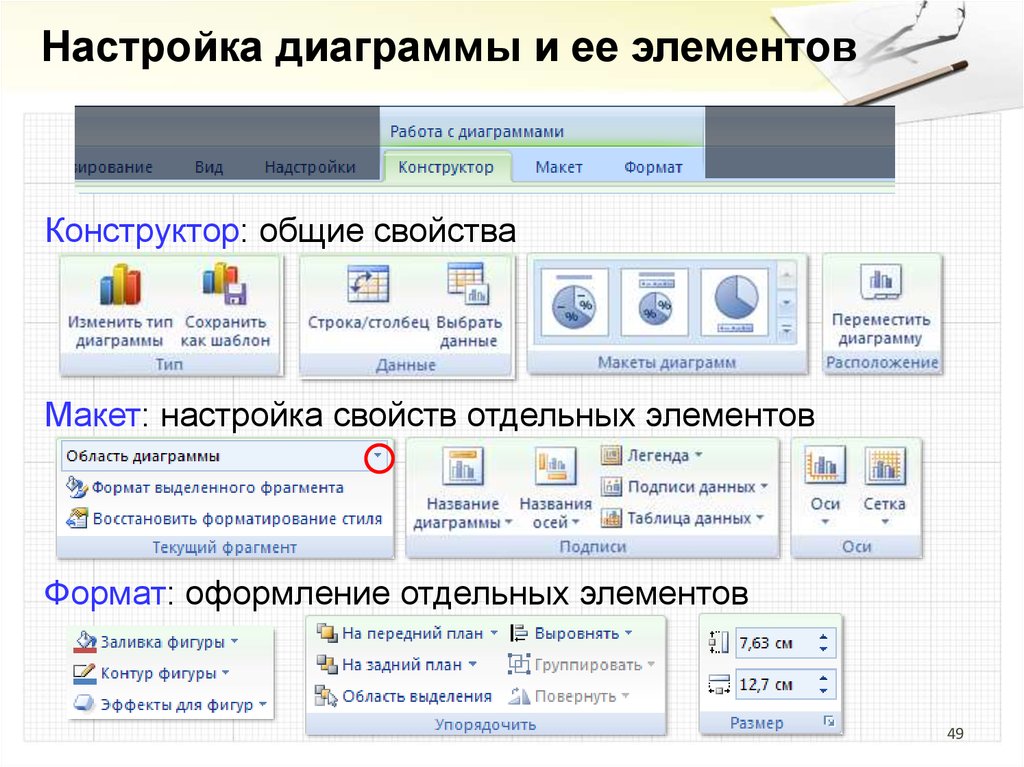
49.
Настройка диаграммы и ее элементовКонструктор: общие свойства
Макет: настройка свойств отдельных элементов
Формат: оформление отдельных элементов
49
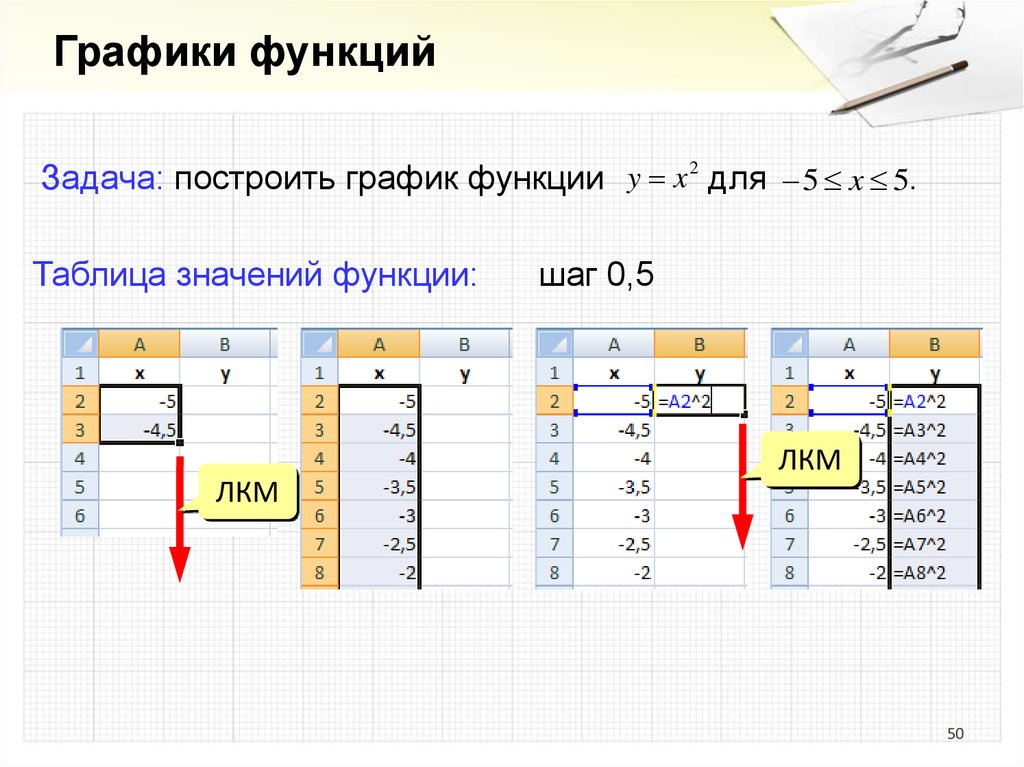
50.
Графики функцийЗадача: построить график функции y x 2 для 5 x 5.
Таблица значений функции:
шаг 0,5
ЛКМ
ЛКМ
50
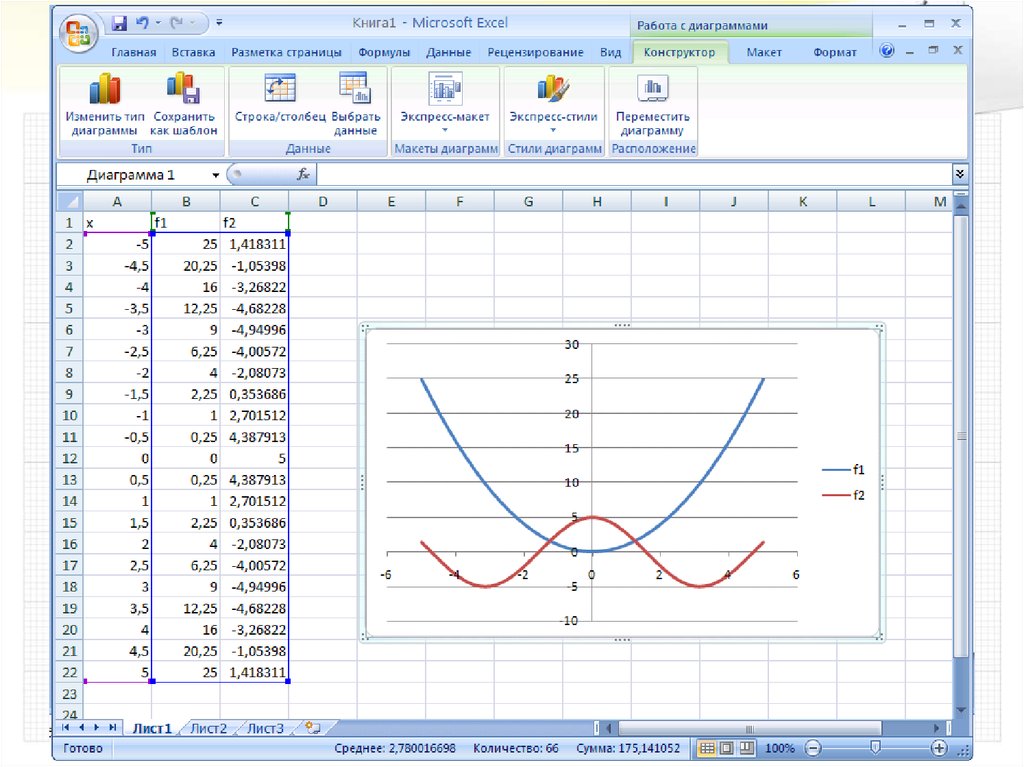
51.
Графики функцийВставка диаграммы «Точечная»:
выделить данные
результат:
51
52.
Решение уравненийЗадача: найти все решения уравнения x 2 5 cos x
на интервале [-5,5]
?
Как решить математическими методами?
Методы решения уравнений:
• аналитические: решение в виде формулы x ...
• численные: приближенное решение, число
1) выбрать начальное приближение x0 «рядом» с
решением
?
Как выбрать начальное приближение?
2) по некоторому алгоритму вычисляют первое
приближение, затем – второе и т.д. x0 x1 x2 ...
3) вычисления прекращают, когда значение меняется очень
*
мало (метод сходится) x0 ... x15 x16 x
52
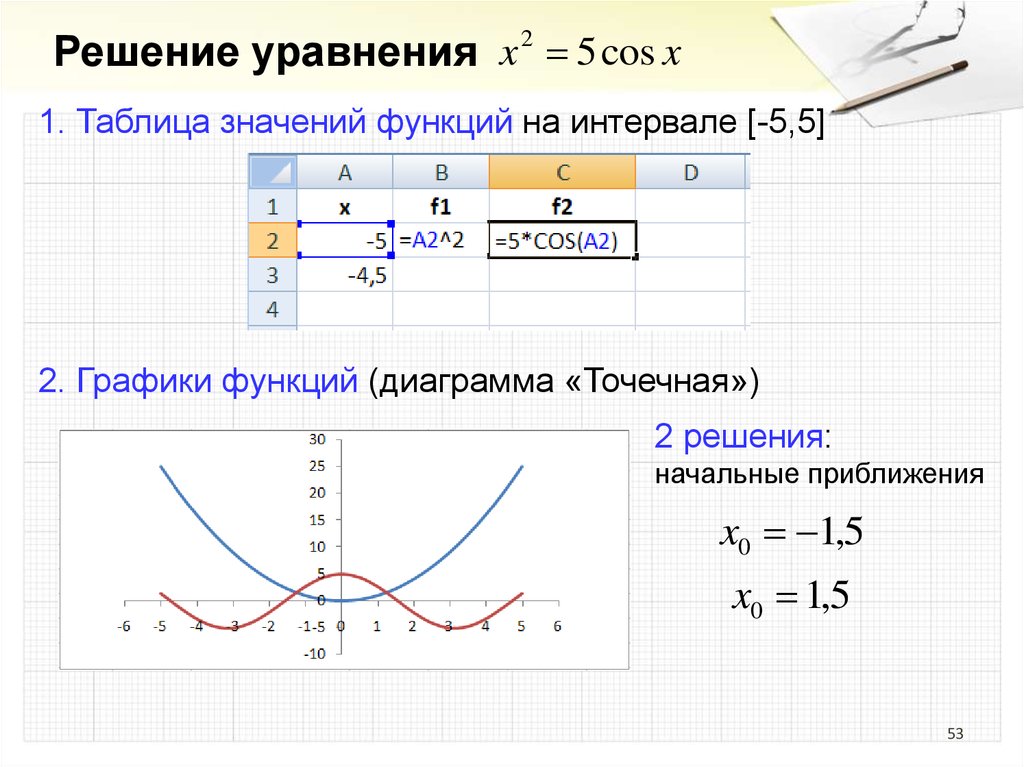
53.
Решение уравнения x 2 5 cos x1. Таблица значений функций на интервале [-5,5]
2. Графики функций (диаграмма «Точечная»)
2 решения:
начальные приближения
x0 1,5
x0 1,5
53
54.
55.
Решение уравненияx 2 5 cos x
3. Подготовка данных
начальное
приближение
целевая
ячейка
Цель: H2=0
?
Зачем нужна разность?
55
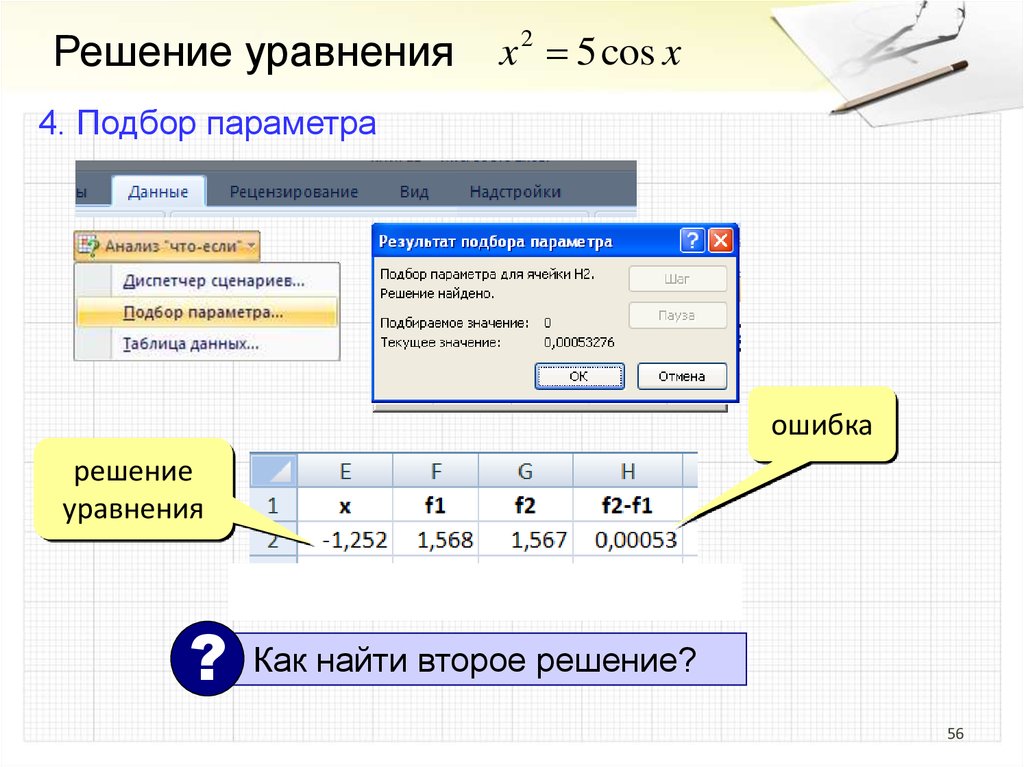
56.
Решение уравненияx 2 5 cos x
4. Подбор параметра
ошибка
решение
уравнения
?
Как найти второе решение?
56
57.
ОптимизацияОптимизация – это поиск оптимального (наилучшего)
варианта в заданных условиях.
Оптимальное решение – такое, при котором некоторая
заданная функция (целевая функция) достигает
минимума или максимума.
Постановка задачи:
• целевая функция
f ( x) min
f ( x) max
(расходы, потери, ошибки)
(доходы, приобретения)
• ограничения, которые делают задачу осмысленной
Задача без ограничений: построить дом
при минимальных затратах.
Решение: не строить дом вообще.
57
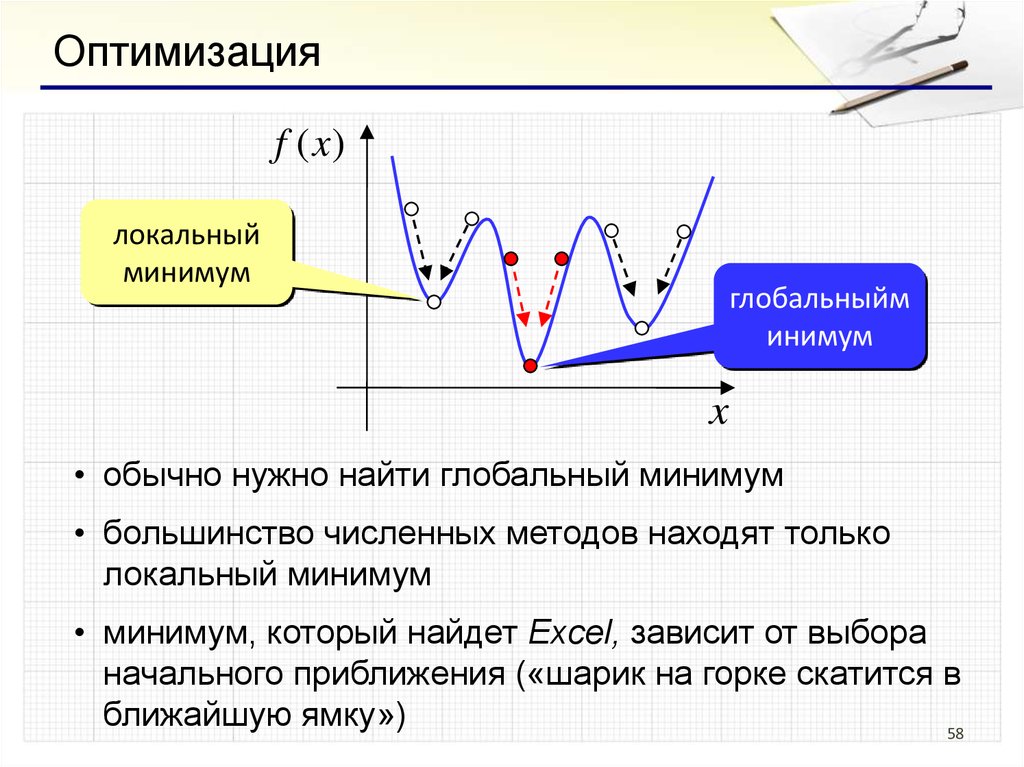
58.
Оптимизацияf (x)
локальный
минимум
глобальныйм
инимум
x
• обычно нужно найти глобальный минимум
• большинство численных методов находят только
локальный минимум
• минимум, который найдет Excel, зависит от выбора
начального приближения («шарик на горке скатится в
ближайшую ямку»)
58
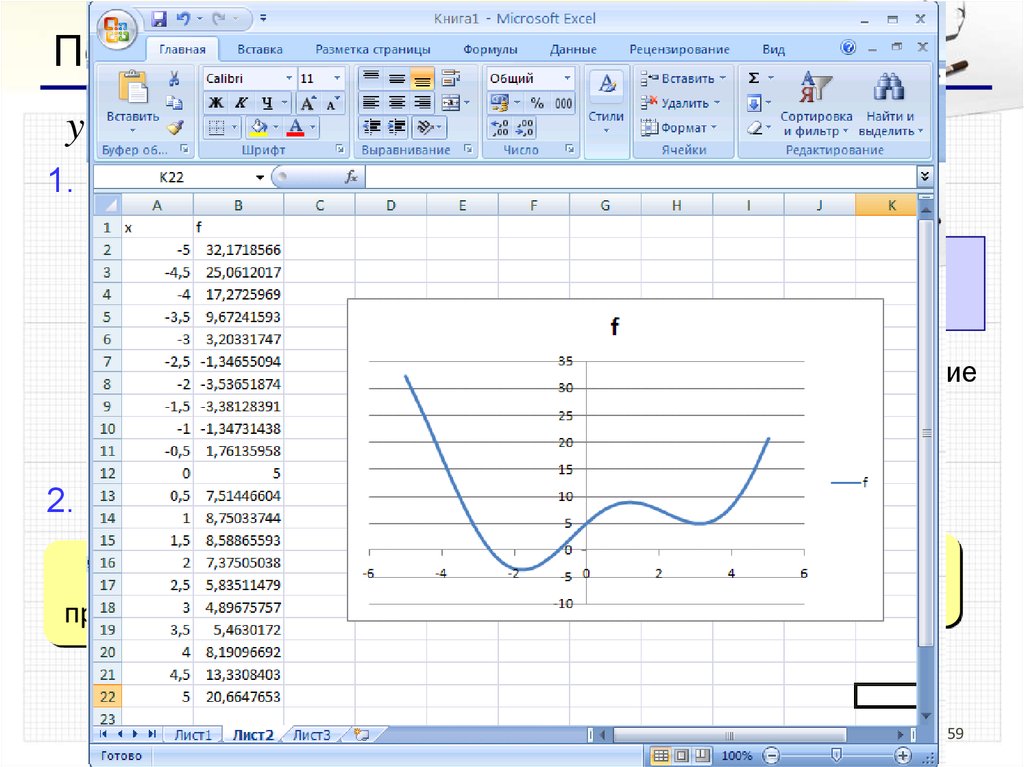
59.
Поиск минимума функцииy x 2 6 sin x 5 cos x
1. Строим график функции (диаграмма «Точечная»)
?
Зачем нужен
график?
начальное приближение
x0 2
2. Подготовка данных
начальное
приближение
!
целевая
ячейка
Изменение E2 должно влиять на F2!
59
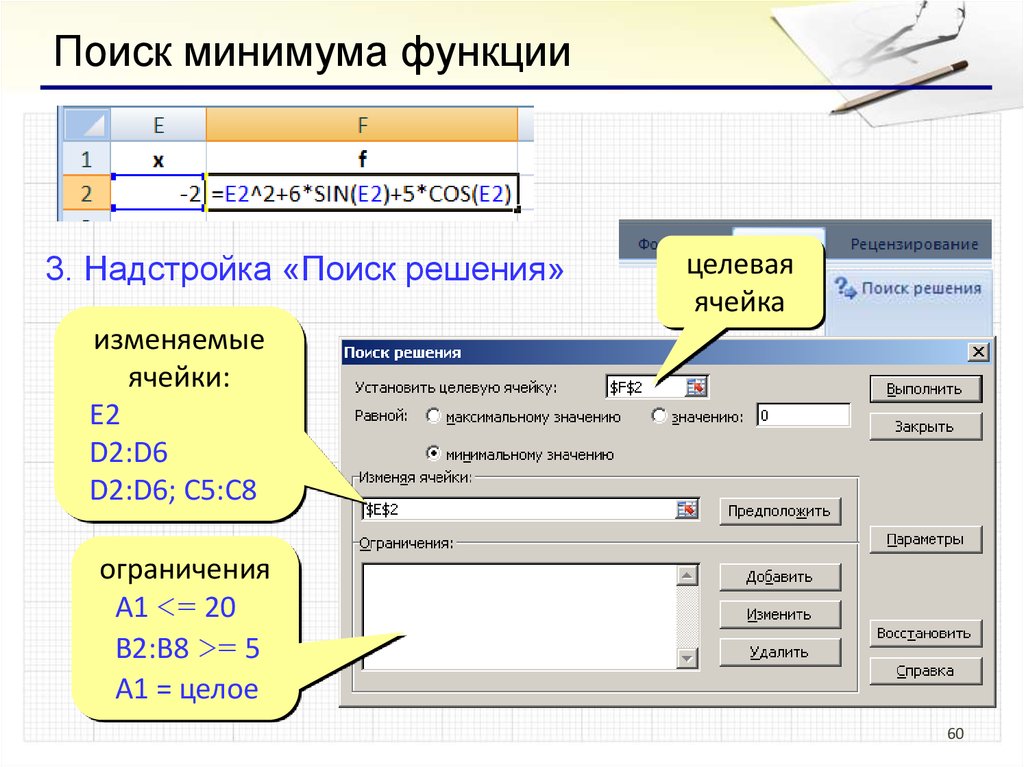
60.
Поиск минимума функции3. Надстройка «Поиск решения»
целевая
ячейка
изменяемые
ячейки:
E2
D2:D6
D2:D6; C5:C8
ограничения
A1 <= 20
B2:B8 >= 5
A1 = целое
60
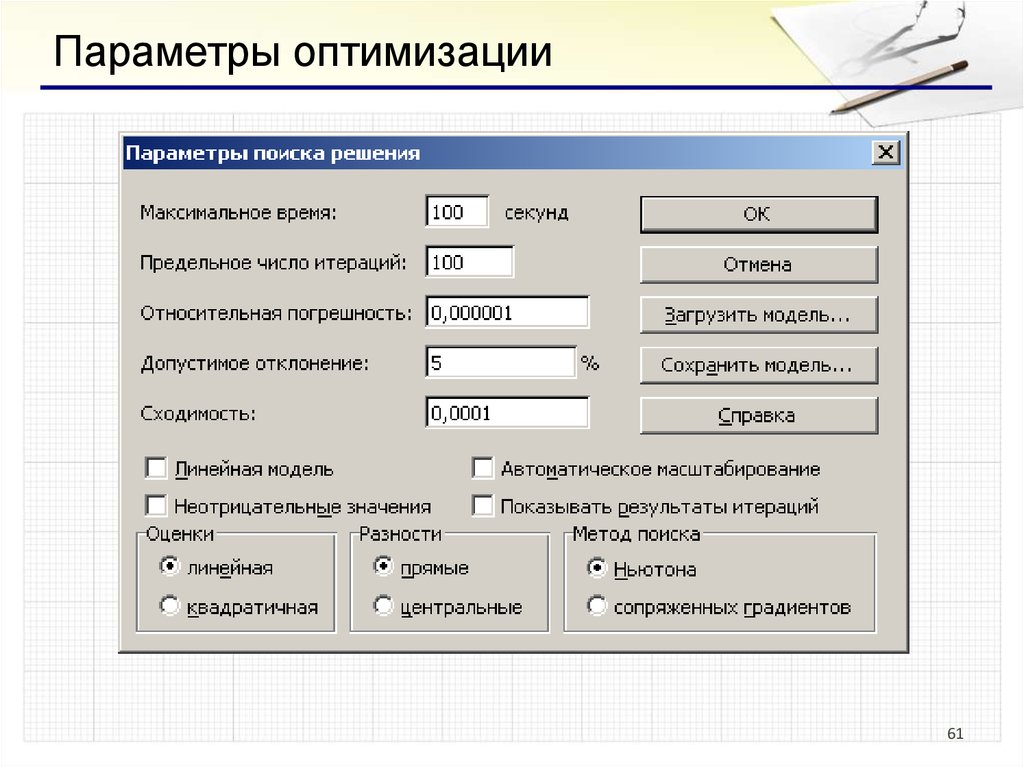
61.
Параметры оптимизации61
62.
Оптимизация?
Подбор параметра – это оптимизация?
Надстройка «Поиск решения» позволяет:
• искать минимум и максимум функции
• использовать несколько изменяемых ячеек и
диапазонов
• вводить ограничения (<=, >=, целое, двоичное)
?
Как влияет ограничение «A1-целое» на
сложность решения задачи?
62



































 Программное обеспечение
Программное обеспечение








