Работа электрического поля. (10 класс)

1. Работа электрического поля

10 класс

2.

Работа электростатического поля
Знак потенциальной энергии в механике
Знак потенциальной энергии в электростатике
Независимость работы от траектории
Потенциал электрического поля
Напряженность и напряжение
Энергия и потенциал точечного заряда
Заряды и массы. Аналогия.
Эквипотенциальные поверхности
выход

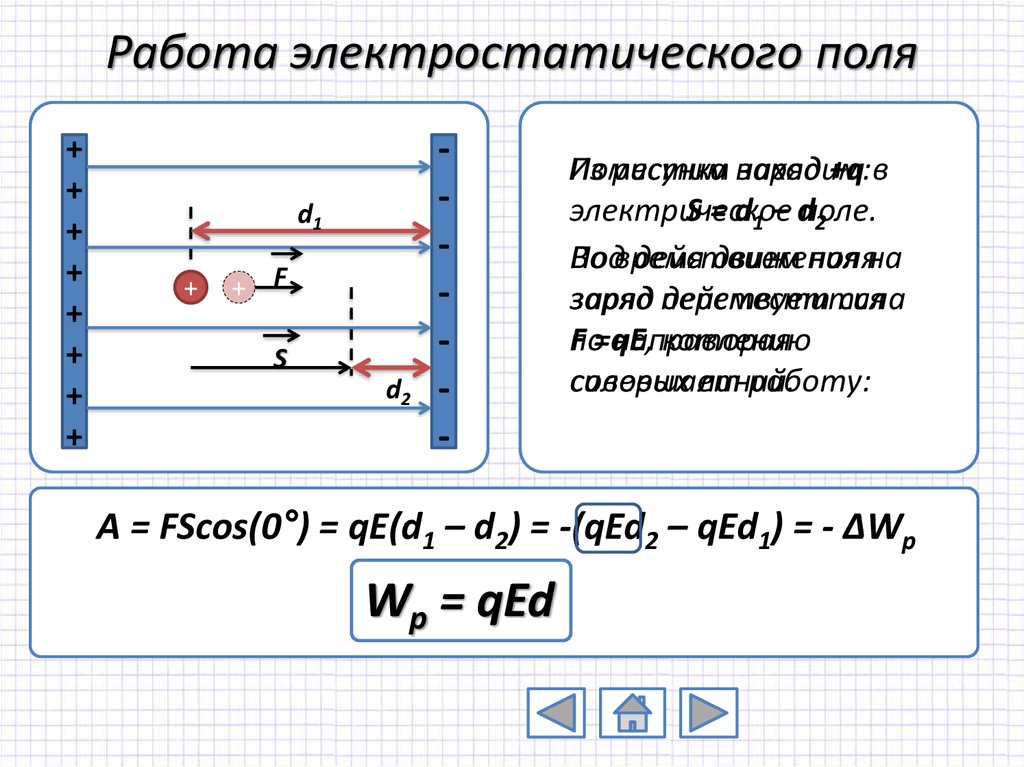
3. Работа электростатического поля

+
+
+
+
+
+
+
+
d1
+
+ F
S
d2
-
Из
Поместим
рисунка находим:
заряд +q в
электрическое
S = d1 – dполе.
2
Под
Во время
действием
движения
поляна
заряд переместится
действует сила
по
F =qE,
направлению
которая
силовых
совершает
линий.
работу:
A = FScos(0°) = qE(d1 – d2) = -(qEd2 – qEd1) = - ΔWp
Wp = qEd

4. Аналогия с работой силы тяжести

Заряд q перемещается
в электрическом поле
Тело массы m перемещается
в поле силы тяжести
+
F = qE
d1
F = mg
h1
+
d2
----------
Wp = qEd
Aэл.поля = -ΔWp
h2
A = FScos(0)
= mg(h1 – h2)
Wp = mgh
= -(mgh2 – mgh1) = - ΔEp
Aтяж = -ΔWp

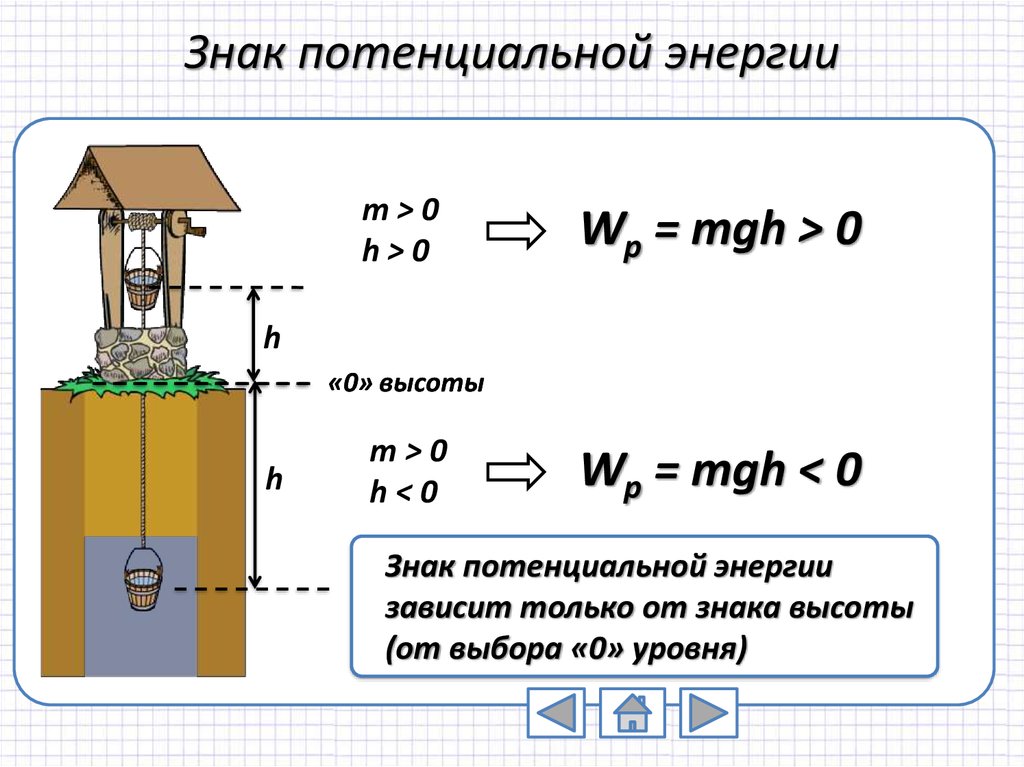
5. Знак потенциальной энергии

m>0
h>0
Wp = mgh > 0
h
«0» высоты
h
m>0
h<0
Wp = mgh < 0
Знак потенциальной энергии
зависит только от знака высоты
(от выбора «0» уровня)

6. Знак потенциальной энергии

Пример 3
1
2
+ + + +
F = qE
F = qE
+-
- - - -
d
«0» уровень
Wp = -|qEd|
+|qEd| <> 00
d
«0» уровень
Знак энергии заряда, находящегося в электрическом
поле, зависит: от направления поля, знака заряда и
выбора «0» уровня

7. Знак потенциальной энергии

Знак потенциальной энергии равен знаку
работы электрического поля при
перемещении заряда на «0» уровень.
A = -ΔWp = - (Wp2 – Wp1) = - (0 – Wp1) = Wp1
Пример 1
+
F = qE
A = FScos(0°) > 0
S
Wp = +|qEd|
«0» уровень

8. Знак потенциальной энергии

Второе
Знак
потенциальной
правило:
энергии равен знаку
работы
Если
сила,
электрического
действующая поля
на заряд,
при
перемещении
направлена
назаряда
«0» уровень,
на «0» то
уровень
Wp > 0
A = -ΔWp = - (Wp2 – Wp1) = - (0 – Wp1) = Wp1
Пример 2
+
S
«0» уровень
F = qE
Для
A =перемещения
FScos(180°)на< 0
«0» уровень необходимо
на заряд подействовать
внешней
Wp = силой
-|qEd|
(на рисунке не указана).

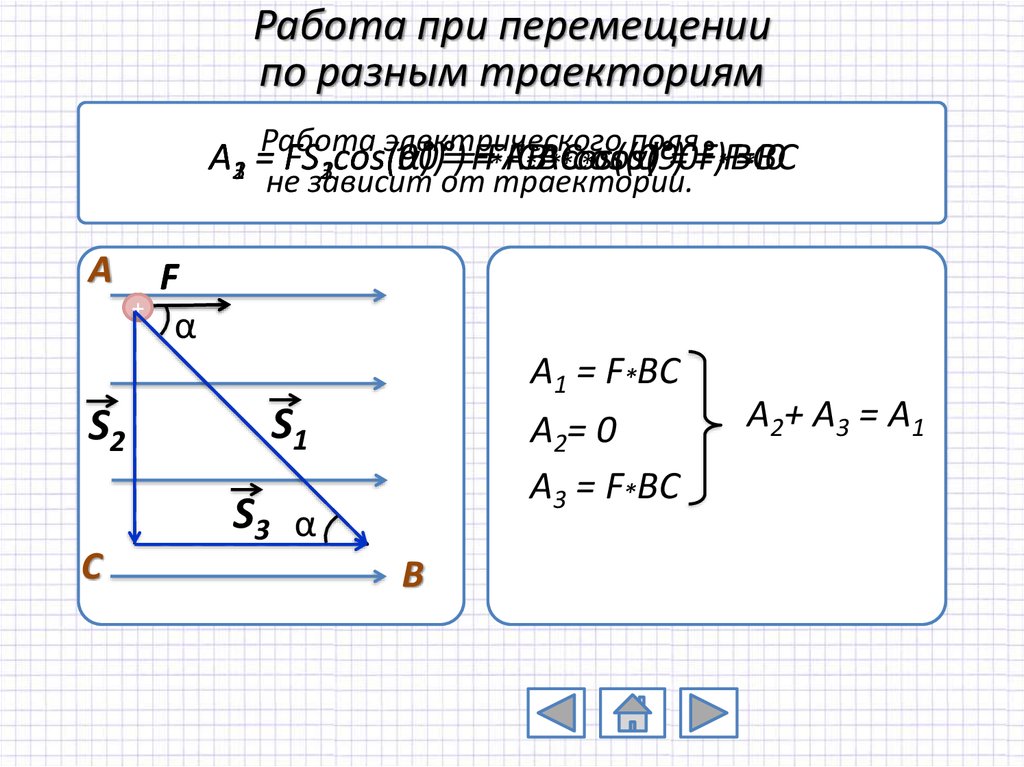
9. Работа при перемещении по разным траекториям

электрического поля
A231 =Работа
FS231cos(α)
= =F*FBC
cos(0°)==F=F*AB
cos(90°)
cos(0°)
=*BC
0
**cos(α)
*FCB
*AC
*cos(90°)
не зависит от траектории.
A
+
S2
F
α
A1 = F*BC
A2= 0
A3 = F*BC
S1
S3 α
C
B
A2+ A3 = A1

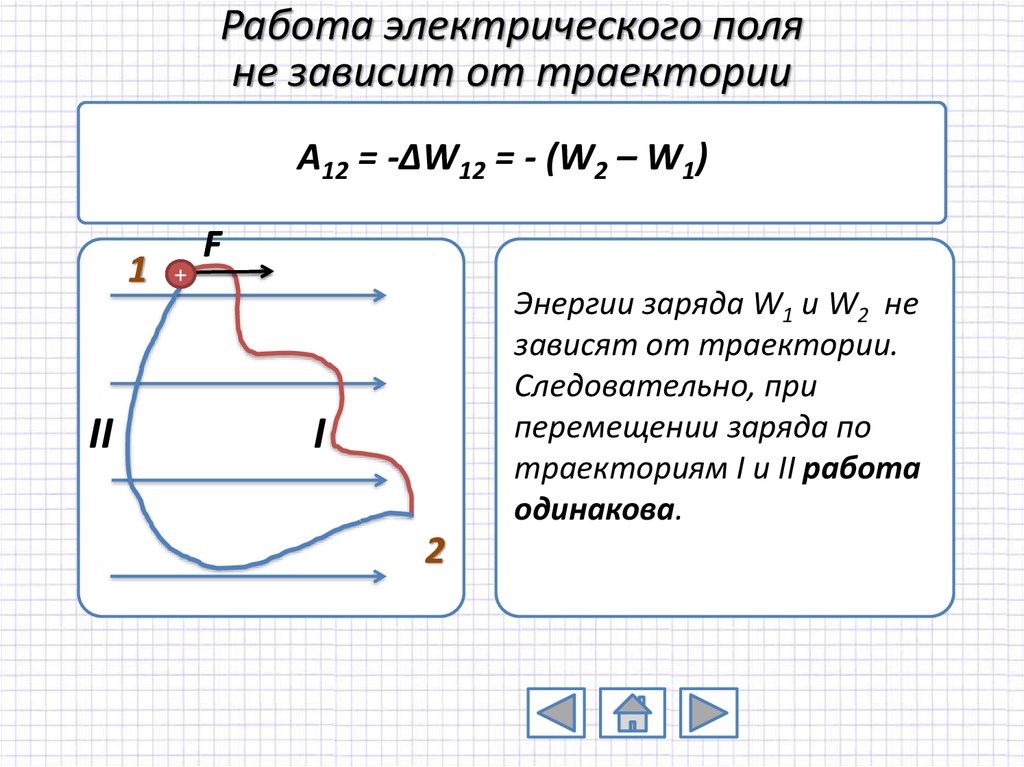
10. Работа электрического поля не зависит от траектории

A12 = -ΔW12 = - (W2 – W1)
1
II
+
F
Энергии заряда W1 и W2 не
зависят от траектории.
Следовательно, при
перемещении заряда по
траекториям I и II работа
одинакова.
I
2

11. Работа при перемещении по замкнутой траектории

При перемещении заряда по замкнутой линии
A
=
FS
cos(α)
=
F
AB
cos(α)
=
F
cos(180°)
cos(90°)
=
F
= 0= - F BC
*=
*BC
*FCA
**BC
*cos(90°)
*cos(180°)
1
1
2
3
2
3
работа электрического поля равна нулю. *
A
+
F
α
S3
C
A1 = F*BC
S1
+
F
S2 α
F
B
A2 = - F*BC
A3= 0
A123= 0

12. Потенциал электрического поля

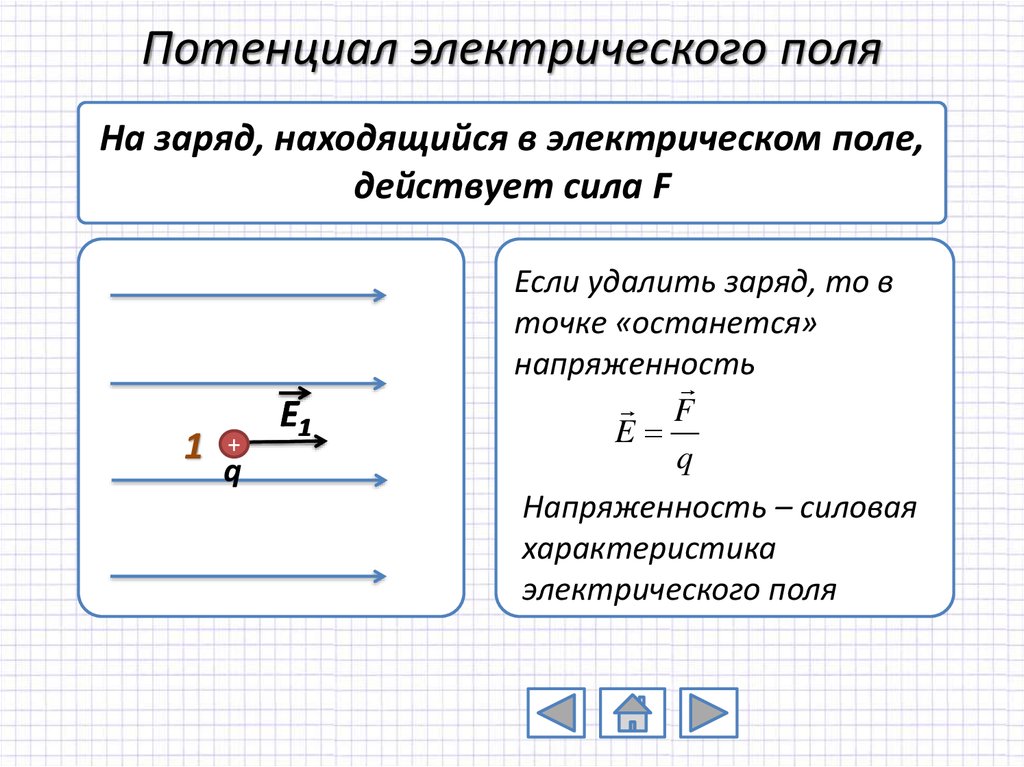
На заряд, находящийся в электрическом поле,
действует сила F
1
+
q
FE1
Если удалить заряд, то в
точке «останется»
напряженность
F
E
q
Напряженность – силовая
характеристика
электрического поля

13. Потенциал электрического поля

Заряд, находящийся
Потенциал –вэнергетическая
электрическом поле,
характеристика
обладает потенциальной
электрического
энергией.
поля
«0» уровень
d1
1
?
+
q
φ1F1
Что «осталось»
Если
удалить заряд,
в точке?
то в
точке «остался»
Wp = |qEd|
потенциал
Wp qEd
Ed
q
q
[Wp ] Дж
[ ]
В
[q]
Кл

14. Напряженность и напряжение

1 - 2 Uзаряд из точки
[U 1
] в точку
В
Переместим
2
E
E
d
φ
q1 F
d
φ2
+
1
Δd
2
[ d ]
м
Работа электрического поля:
A = FS= qEΔd
A = - (Wp2 – Wp1) = Wp2 – Wp1
Wp1 = qφ1; Wp2 = qφ2
A = qEΔd = q(φ1 – φ2) = qU
U = φ1 – φ2 - разность
потенциалов или напряжение

15. Энергия и потенциал точечного заряда

F – изменяется,
следовательно, разобьем
Qq
Q
Переместим
заряд
q
из
точки
a
в
точку
b
Wp k
Wp q k
путь на
r небольшие участки Δr Si
Работа электрического поля:
A = F1ΔS1 + F2ΔS2 + …
+
q ΔSF1 ΔS
S ΔS …
a 2 3
+
Q φa
+
φb
Fb
Qq
Qq
A k 2 S1 k 2 S 2 ...
r1
r2
Qq
Qq
A k
k
ra
rb

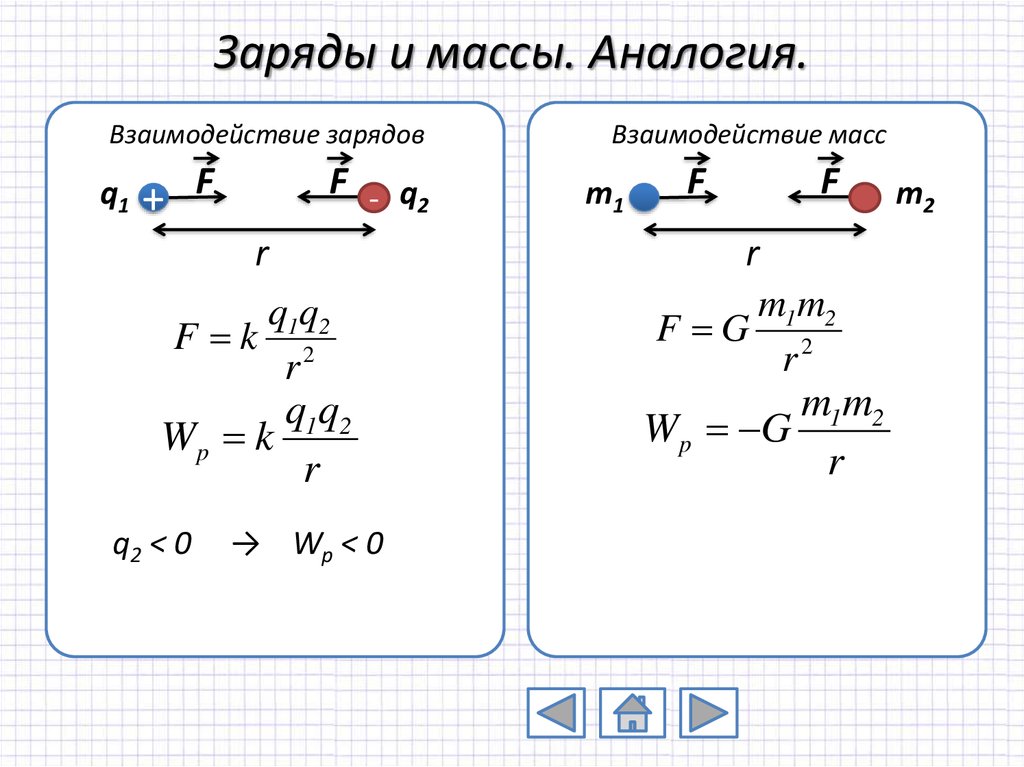
16. Заряды и массы. Аналогия.

Взаимодействие зарядов
q1
+ F
F - q2
r
q1q2
F k 2
r
q1q2
Wp k
r
q2 < 0
→ Wp < 0
Взаимодействие масс
m1
F
F
r
m1m2
F G 2
r
m1m2
Wp G
r
m2

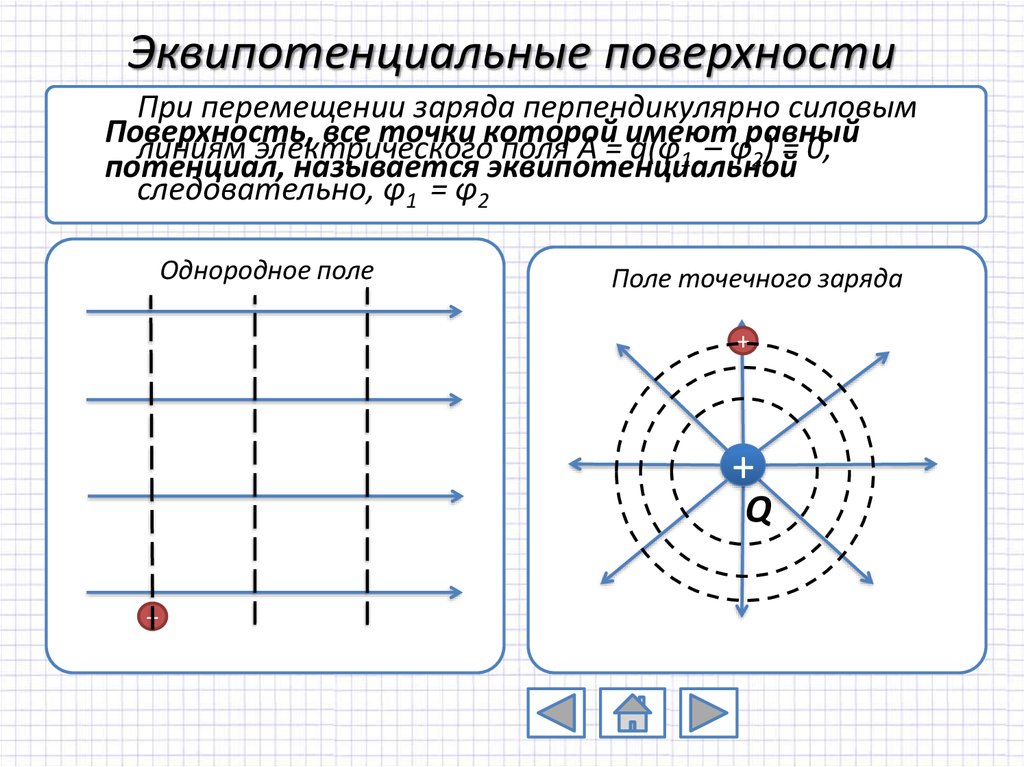
17. Эквипотенциальные поверхности

При перемещении заряда перпендикулярно силовым
Поверхность,
все точки которой
линиям электрического
поля A = имеют
q(φ1 – φравный
2) = 0,
потенциал, называется эквипотенциальной
следовательно, φ1 = φ2
Однородное поле
Поле точечного заряда
+
+
Q
+