Выбор нескольких элементов

1.

Выбор нескольких элементов

2.

Пример 1.
В чемпионате участвовали 7 команд. Каждая команда играла
один матч с каждой. Сколько всего было встреч?
Решение :
Рассмотрим таблицу
результатов встреч размером
7x7.
Так как никакая команда не
играет сама с собой, то клетки
по диагонали надо закрасить.
Тогда в подсчете числа встреч
будет участвовать ровно
72 - 7 = 7(7 - 1) = 42 клетки.

3.

В результате закрашивания таблица разделилась на две
половинки, в них результаты встреч команд дублируются.
Поэтому если мы разделим оставшиеся 42 клетки на две
равные половины, то получим число всех проведенных игр.
7 7 1
21
2
Важно при этом то, что порядок выбора не имеет
значения, т. е. если выбраны две команды, то какая из них
первая, а какая вторая – не важно.

4.

Теорема о выборках двух элементов
Если множество состоит из п элементов, то у него
имеется n n 1 подмножеств, состоящих из двух элементов.
2
Иными словами, если множество состоит из п элементов и
требуется выбрать из них два элемента без учета их порядка,
то такой выбор можно произвести n n 1 способами.
2

5.

Пример 2
В классе 27 учеников. К доске нужно вызвать двоих. Сколькими
способами это можно сделать, если: а) первый ученик должен
решить задачу по алгебре, а второй – по геометрии; б) они
должны быстро стереть с доски?
Решение:
Для стирания с доски порядок вызова учеников не важен. А вот в первом
случае порядок существенен. Тут применимо правило умножения.
Учитель сначала вызывает решать алгебраическую задачу одного из 27
учеников, а затем независимым образом вызывает одного из оставшихся
26 учеников решать задачу по геометрии. Получается 27 • 26 = 702
способа вызова.
Если во втором случае начать считать, как и в первом, то любую пару
учеников мы посчитаем дважды. Например, сначала Коля, потом Катя,
или сначала Катя, потом Коля. Значит, количество вызовов без учета
порядка будет ровно в два раза меньше, чем количество вызовов с
учетом порядка.
Ответ: а) 702; 6) 351.

6.

Всегда количество выборок двух элементов без учета порядка будет ровно в
два раза меньше, чем количество выборок с учетом порядка. На рисунке
представлена соответствующая схема.
Число всех выборок из n данных без учета порядка обозначается
называется числом сочетаний из n элементов по 2.
n n 1
C
2!
2
n
и

7.

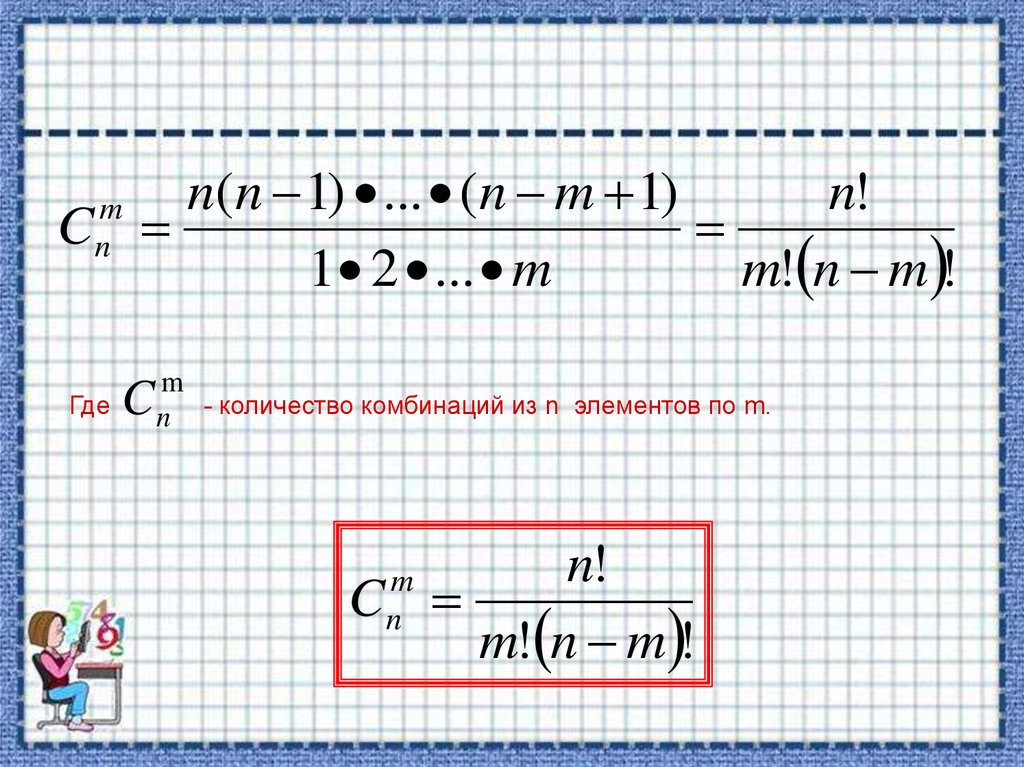
n(n 1) ... (n m 1)
n!
C
1 2 ... m
m! n m !
m
n
Где
C
m
n - количество комбинаций из n элементов по m.
n!
C
m! n m !
m
n

8.

Пример 3.
В классе 27 учеников, из которых нужно выбрать троих. Сколькими
способами это можно сделать, если: а) первый ученик должен решить
задачу, второй – сходить за мелом, третий – пойти дежурить в столовую;
б) им следует спеть хором?
а) 27 26 25 17550 (важен порядок вызова
учеников)
б)
27!
27! 27 26 25 27 26 25
С
2925
3! 27 3 ! 3!24!
3 2 1
6
3
27
(порядок не важен)
Ответ. а)17550; б) 2925

9.

Пример 4.
«Проказница Мартышка, Осел, Козел и косолапый Мишка
затеяли сыграть квартет». Мишке поручили принести со склада
8 каких-нибудь попавшихся под лапы музыкальных
инструментов из имеющихся 13 инструментов. Сколько
способов выбора есть у Мишки?
13!
13 12 11 10 9
C
8! 13 8 !
5 4 3 2 1
13 11 9 1287
8
13

10.

Биномиальные коэффициенты
В математике биномиальные коэффициенты — это коэффициенты
в разложении бинома Ньютона
по степеням x. Коэффициент
при
обозначается
или
и читается «биномиальный коэффициент
из n по k» (или «це из n по k»):
причём n здесь может быть как целым, так и произвольным действительным
числом. Для неотрицательных целых n все коэффициенты с индексами k>n в
этом ряду являются нулевыми, и поэтому данное разложение представляет
собой конечную сумму

11.

Значение биномиального коэффициента определено для всех
действительных чисел n и целых чисел k по формулам:
где
обозначает факториал числа m.
Факториа́л числа n — произведение всех натуральных чисел
от 1 до n включительно:

12.

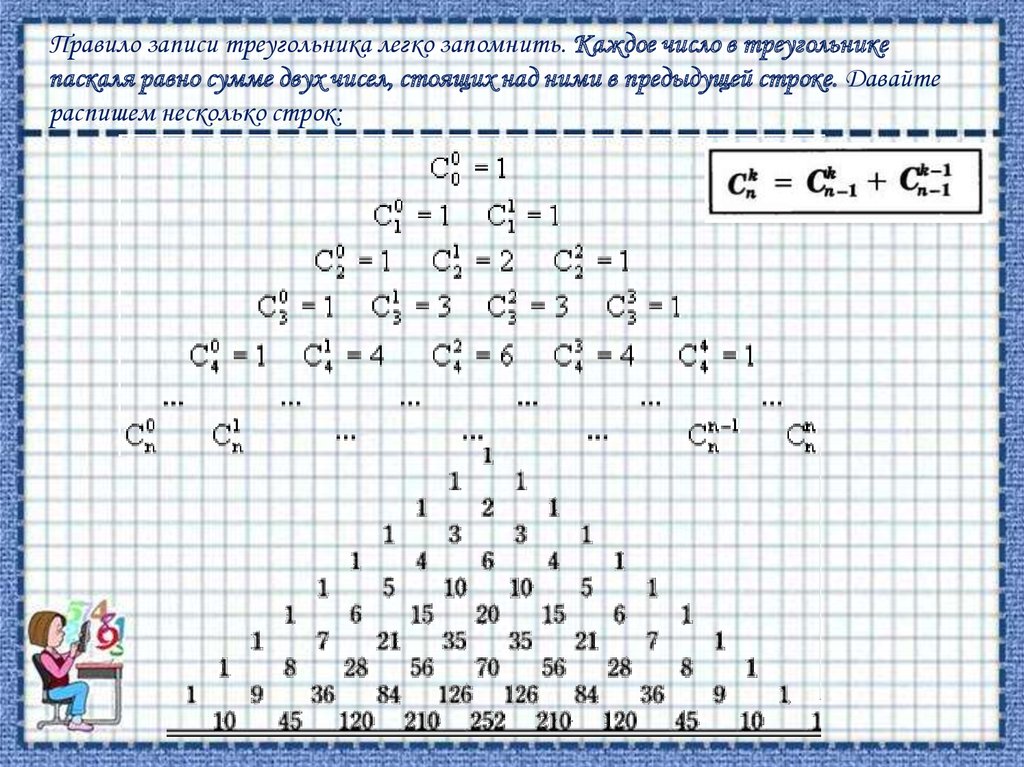
Для неотрицательных целых n и k также справедливы формулы:
Треугольник Паскаля
Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов,
имеющая треугольную форму. В этом треугольнике на вершине и по бокам
стоят единицы. Каждое число равно сумме двух расположенных над ним чисел.
Строки треугольника симметричны относительно вертикальной оси. Назван в
честь Блеза Паскаля. Числа, составляющие треугольник Паскаля, возникают
естественным образом в алгебре, комбинаторике, теории
вероятностей, математическом анализе, теории чисел.

13.

14.

•Числа треугольника симметричны (равны)
относительно вертикальной оси.
•В строке с номером n:
•первое и последнее числа равны 1.
•второе и предпоследнее числа равны n.
•третье число равно треугольному числу
,
что также равно сумме номеров предшествующих
строк.
•четвёртое число является тетраэдрическим.
•m-е число (при нумерации с 0) равно биномиальному
коэффициенту

15.

Правило записи треугольника легко запомнить. Каждое число в треугольнике
паскаля равно сумме двух чисел, стоящих над ними в предыдущей строке. Давайте
распишем несколько строк:

16.

Вспомним некоторые формулы сокращенного умножения
– формула квадрата суммы.
Рассмотрим, как вывести эту
формулу.
раскрываем скобки, перемножая почленно:
Аналогично, для куба суммы

17.

Выпишем для наглядности все наши формулы:
Проведем небольшой анализ полученных формул.
Обратить внимание: показатель степени в левой части равен сумме
показателей степеней в правой части для любого слагаемого.
Для четвертой степени, очевидно, что слева показатель равен 4. В правой
части показатель степени при первом слагаемом равен для а четырем,
для b нулю и в сумме равен 4.
Для второго слагаемого сумма показателей равна 3+1=4, для следующего 2+2=4и так до самого конца сумма показателей равна 4.

18.

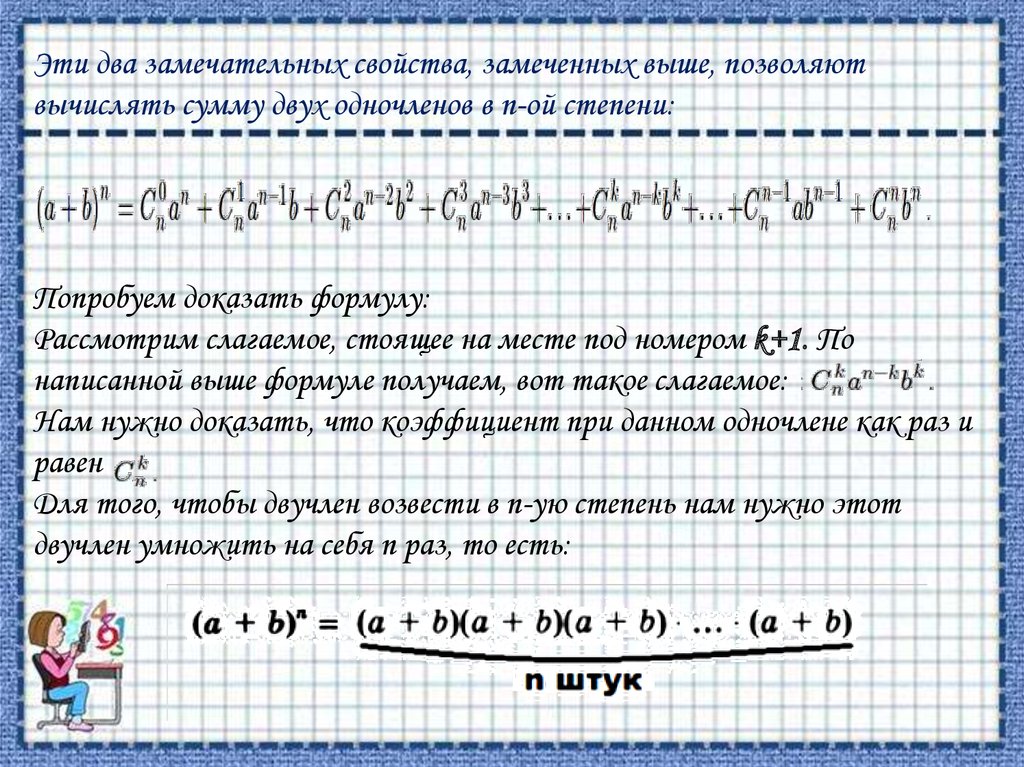
Эти два замечательных свойства, замеченных выше, позволяют
вычислять сумму двух одночленов в n-ой степени:
Попробуем доказать формулу:
Рассмотрим слагаемое, стоящее на месте под номером k+1. По
написанной выше формуле получаем, вот такое слагаемое:
Нам нужно доказать, что коэффициент при данном одночлене как раз и
равен
Для того, чтобы двучлен возвести в n-ую степень нам нужно этот
двучлен умножить на себя n раз, то есть:

19.

Чтобы получить требуемое слагаемое надо выбрать k штук
множителей для b. Тогда получается n−k множителей для а. В
каком порядке будем выбирать данные множители не важно. Эта
задача есть ни что иное как: число сочетаний из n элементов по k
без повторений или
Наша формула доказана.
Полученная нами формула называется "Бином Ньютона".
Коэффициенты, стоящие перед слагаемыми,
это биномиальные коэффициенты.