Похожие презентации:
Дифференциальное исчисление функций нескольких переменных
1. Дифференциальное исчисление функций нескольких переменных
2. Функция n переменных
Переменная u называется функцией n переменных(аргументов) x,y,z,…,t, если каждой системе значений
x,y,z,…,t, из области их изменений (области определения),
соответствует определенное значение u.
Областью
определения
функции
называется
совокупность всех точек, в которых она имеет
определенные действительные значения.
Для функции двух переменных z=f(x,y) область
определения представляет некоторую совокупность точек
плоскости, а для функции трех переменных u=f(x,y,z) –
некоторую совокупность точек пространства.
3. Функция двух переменных
Функцией двух переменных называется закон,по
которому
каждой
паре
значений
независимых переменных x,y (аргументов)
из области определения соответствует
значение зависимой переменной z (функции).
Данную функцию обозначают следующим
образом: z = z(x,y) либо z= f(x,y) , или же
другой стандартной буквой: u=f(x,y) , u = u (x,y)
4. Частные производные первого порядка
Частной производной от функции z =f(x,y) по независимойпеременной х называется конечный предел
f ( х х, у ) f ( х, у ) z
lim
f х ( х, у )
х 0
х
х
вычисленный при постоянной у
Частной производной по у называется конечный предел
f ( х, y у ) f ( х, у ) z
lim
f y ( х, у )
y 0
y
y
вычисленный при постоянной х
Для частных производных справедливы обычные правила
и формулы дифференцирования.
5. Полный дифференциал
Полный дифференциал функции z =f(x,y)вычисляется по формуле
z
z
dz dх dу
х
y
Полный дифференциал функции трех
аргументов u =f(x,y,z) вычисляется по
формуле
u
u
u
du dх dу dz
х
y
z
6. Частные производные высших порядков
Частными производными второго порядка от функции z =f(x,y)называются частные производные от ее частных производных
первого порядка
z 2 z
2 f хх ( х, у );
х х х
z 2 z
f ху ( х, у );
у х х у
z 2 z
f ух ( х, у );
х у у х
z 2 z
2 f уу ( х, у );
у у у
Аналогично определяются и обозначаются частные
производные третьего и высших порядков
.
2 z 3z
( х, у );
2 3 f ххх
х х х
2 z 3z
( х, у ) и т.д.
2 2 f хху
у х х у
7. Дифференциалы высших порядков
Дифференциалом второго порядка от функцииz=f(x,y) называется дифференциал от ее пологого
2z 2
2z
2z 2
d z 2 dх 2
dxdy 2 dу
х y
х
y
2
Дифференциалы высших порядков вычисляются по
формуле
3
3
3
3
z
z
z
z 3
3
3
2
2
d z 3 dх 3 2 dx dy 3
dxdy 3 dу
2
х
х y
х y
y
Имеет место символическая формула
n
d n z dх dу z
y
х
8. Дифференцирование сложных функций
Пусть z=f(x,y), где х=φ(t), у=ψ(t) и функцииf(x,y), φ(t), ψ(t) дифференцируемы. Тогда
производная сложной функции z=f[φ(t),ψ(t)]
вычисляется по формуле
dz z dх z dу
dt х dt y dt
9. Дифференцирование неявных функций
Производныенеявной
функции
двух
переменных z=f(x,y), заданной с помощью
уравнения F(x,y,z)=0, могут быть вычислены
по формулам
dz
F / dx dz
F / dy
,
dx
F / dz dy
F / dz
dF
при условии
0
dz
10. Экстремум функции
Функции z=f(x,y) имеет максимум (минимум) вточке M0(x0;y0) если значение функции в этой
точке больше (меньше), чем ее значение в любой
другой точке M(x;y) некоторой окрестности точки
M0.
Если дифференцируемая функция z=f(x,y)
достигает экстремума в точке M0(x0;y0), то ее
частные производные первого порядка в этой
точке равны нулю, т.е.
df ( х0 , у0 )
df ( х0 , у0 )
0,
0
dx
dу
(необходимые условия экстремума).
11.
Пусть M0(x0;y0) - стационарная точка функцииz=f(x,y). Обозначим
d 2 f ( х0 , у 0 )
d 2 f ( х0 , у 0 )
d 2 f ( х0 , у 0 )
А
, В
, С
2
dxdу
dx
dу 2
И составим дискриминант Δ=AC-B2. Тогда:
Если Δ>0, то функция имеет в точке М0
экстремум, а именно максимум при А<0 (или
С<0) и минимум А>0 (или С>0);
Если Δ<0, то в точке М0 экстремума нет
(достаточные условия наличия или отсутствия
экстремума);
Если
Δ=0,
то
требуется
дальнейшее
исследование (сомнительный случай).
12. Неопределённый интеграл
13. Первообразная функция
• Функция F(x) называется первообразной дляфункции f(x) на интервале X=(a,b), если в
каждой точке этого интервала f(x) является
производной для F(x), т.е.
F ( x) f ( x)
• Из этого определения следует, что задача
нахождения первообразной обратна задаче
дифференцирования: по заданной функции
f(x)
требуется
найти
функцию
F(x),
производная которой равна f(x).
14. Неопределённый интеграл
• Множество всех первообразных функцииF(x)+С для f(x) называется неопределённым
интегралом от функции f(x) и обозначается
символом
f ( x )dx . Таким образом, по
определению
f ( x)dx F ( x) C
где C - произвольная постоянная;
f(x) - подынтегральная функция;
f(x) dx - подынтегральное выражение;
x - переменная интегрирования;
- знак неопределенного интеграла.
15. Свойства неопределённого интеграла
1. Дифференциал от неопределенного интеграла равенподынтегральному
выражению,
а
производная
неопределенного интеграла равна подынтегральной
функции:
d
f ( x)dx f ( x)dx, f ( x)dx f ( x)
2. Неопределенный интеграл от дифференциала
некоторой функции равен сумме этой функции и
произвольной постоянной:
dF ( x) F ( x) C
16.
3. Постоянный множитель можно вынести за знакинтеграла:
аf ( x)dx а f ( x)dx,
а 0 постоянная
4. Неопределенный интеграл от алгебраической суммы
конечного числа непрерывной функций равен
алгебраической сумме интегралов от слагаемых
функций:
f ( x) g ( x) dx f ( x)dx g ( x)dx
5. Если f ( x)dx F ( x) C , то и f (u )du F (u ) C где
u=φ(x)- произвольная функция, имеющая непрерывную
производную
17. Таблица неопределённых интегралов
18. Основные методы интегрирования
Метод непосредственного интегрирования• Метод интегрирования, при котором данный
интеграл путем тождественных преобразований
подынтегральной функции (или выражения) и
применения свойств неопределенного интеграла
приводится к одному или нескольким табличным
интегралам,
называется
непосредственным
интегрированием.
19.
• Присведении
данного
интеграла
к
табличному часто используются следующие
преобразования дифференциала (операция
«подведения под знак дифференциала»):
du d (u a ), a число,
cos udu d (sin u ),
1
du d ( au ), a 0 число,
a
1
u du d (u 2 ),
2
sin udu d (cos u ),
1
du d (ln u ),
u
1
du d (tgu).
2
cos u
20. Замена переменной в неопределённом интеграле (интегрирование подстановкой)
• Метод интегрирования подстановкой заключается вовведении новой переменной интегрирования. При этом
заданный интеграл приводится к новому интегралу,
который является табличным или к нему сводящимся.
• Пусть требуется вычислить интеграл f ( x )dx. Сделаем
подстановку х = φ(t), где φ(t) - функция, имеющая
непрерывную производную.
• Тогда dx=φ'(t)dt и на основании свойства инвариантности
формулы интегрирования неопределенного интеграла
получаем формулу интегрирования подстановкой
f ( x)dx f ( (t )) (t )dt
21. Интегрирование по частям
• Формула интегрирования по частямd (uv) udv vdu
или
u dv uv v du
• Формула
дает
возможность
свести
вычисление интеграла udv к вычислению
интеграла vdu , который может оказаться
существенно
более
простым,
чем
исходный.
22. Интегрирование рациональных дробей
• Рациональной дробью называется дробь вида P(x)/Q(x), гдеP(x) и Q(x) – многочлены. Рациональная дробь называется
правильной, если степень многочлена P(x) ниже степени
многочлена Q(x); в противном случае дробь называется
неправильной.
• Простейшими (элементарными) дробями называются
правильные дроби следующего вида:
где А, В, p, q, a - действительные числа.
23. Найдем интегралы от простейших дробей
24.
Первый интеграл простейшей дроби IV типа вправой части равенства легко находится с помощью
подстановки х2+px+q=t, а второй преобразуем так:
x
dx
2
px q
m
dx
p
p
x q
2
4
2
x
2
px q
m
и обозначая q-p2/4=a2,
Полагая х+р/2=t, dx=dt
получим
dx
2
m
t
dt
2
a
2 m
25. Интегрирование рациональных дробей с помощью разложения на простейшие дроби
Перед интегрированием рациональной дроби P(x)/Q(x) надо сделатьследующие алгебраические преобразования и вычисления:
1)Если дана неправильная рациональная дробь, то выделить из нее
целую часть, т.е. представить в виде
P1 ( x)
P( x)
М ( x)
Q( x)
Q( x)
где М(х)-многочлен, а P1(x)/Q(x) – правильная рациональная дробь;
2) Разложить знаменатель дроби на линейные и квадратичные
множители:
n
Q( x) ( x a) ..... x px q ....,
m
2
где р2/4-q<0, т.е. трехчлен х2+рх+q имеет комплексные сопряженные
корни;
26.
3) Правильную рациональную дробь разложить на простейшиедроби:
Am
P1 ( x)
A1
A2
...
....
m
m 1
Q( x) ( x a)
x a
( x a)
Bn x C n
B1 x C1
B2 x C 2
.... 2
2
.... 2
....;
n
n 1
( x px q)
( x px q)
x px q
4) Вычислить неопределенные коэффициенты А1, А2, …, Аm, …, В1,
В2, …, Вm, …, С1, С2, …, Сm, …, для чего привести последнее
равенство к общему знаменателю, приравнять коэффициенты
при одинаковых степенях х в левой и правой частях полученного
тождества и решить систему линейных уравнений относительно
искомых коэффициентов.
27. Интегрирование простейших иррациональных функций
1.Интегралы видаR( x, (ax b)
m1 / n1
, (ax b)
m2 / n2
,...)dx
где R – рациональная функция; m1,n1,m2,n2,…- целые числа.
С помощью подстановки ах+b=ts, где s- наименьшее общее
кратное чисел n1,n2,…, указанный интеграл преобразуется в
интеграл от рациональной функции.
2. Интеграл вида
dx
аx bx c
2
Такие интегралы путем выделения квадрата из квадратного
трехчлена приводятся к табличным интегралам 15 или 16
28.
3. Интеграл видаАx В
аx bx c
2
dx
Для нахождения этого интеграла выделим в числителе
производную квадратного трехчлена, стоящего под
знаком корня, и разложим интеграл на сумму
интегралов:
Аx В
А d аx 2 bx c
Аb
dx
dx
(В
)
2
2
2а
2а
аx bx c
аx bx c
аx 2 bx c
29.
4.Интегралы вида( х а)
dx
аx 2 bx c
С помощью подстановки х-α=1/t этот интеграл приводится к рассмотренному п.2
5. Интеграл вида
Р ( x)dx
( х а)
n
аx 2 bx c
где Рn(х) – многочлен n-й степени. Интеграл такого вида находится с помощью
тождества
Рn ( x)dx
( х а)
аx 2 bx c
Qn 1 ( x) аx bx c
2
dx
аx 2 bx c
где Qn-1(x) – многочлен (n-1)-й степени с неопределенными коэффициентами, λчисло.
Дифференцируя указанное тождество и приводя результат к общему
знаменателю, получим равенство двух многочленов, из которого можно
определить коэффициенты многочлена Qn-1(x) и число λ.
30.
6. Интегралы от дифференциальных биномовх
(
a
bx
)
dx
m
n
p
где m, n, p – рациональные числа.
Как доказал П.Л. Чебышев, интегралы от дифференциальных
биномов выражаются через элементарные функции только в
трех случаях:
1) р – целое число, тогда данный интеграл сводится к
интегралу от рационнальной функции с помощью
подстановки х=ts, где s – наименьшее общее кратное
знаменателей дробей m и n.
2) (m+1)/n – целое число, в этом случае данный интеграл
рационализируется с помощью подстановки a+bxn=ts;
3) (m+1)/n+р – целое число, в этом случае к той же цели
ведет подстановка ax-n+b=ts , где s – знаменатель дроби р.
31. Интегрирование тригонометрических функций
Интегралы видаR(sin x, cos x)dx
где R – рациональная функция.
Под знаком интеграла находится рациональная функция
от синуса и косинуса. В данном случае применима
универсальная
тригонометрическая
подстановка
tg(x/2)=t, которая сводит этот интеграл к интегралу от
рациональной функции нового аргумента t (таблица п.1).
Существуют и другие подстановки, представленные в
следующей таблице:
32.
33.
34. Определенный интеграл
35.
Определенным интегралом от функции f(x) наотрезке [a;b] называется предел интегральных
сумм при условии, что длина наибольшего
частичного отрезка Δхi стремится к нуль.
b
f ( x)dx
a
n
lim
max xi 0
i 1, 2 ,...,n
f (с ) x
i 1
i
i
Числа а и b называются нижним и верхним
пределами интегрирования.
Теорема Коши. Если функция f(x) непрерывна на
отрезке [a;b], то определенный интеграл
существует
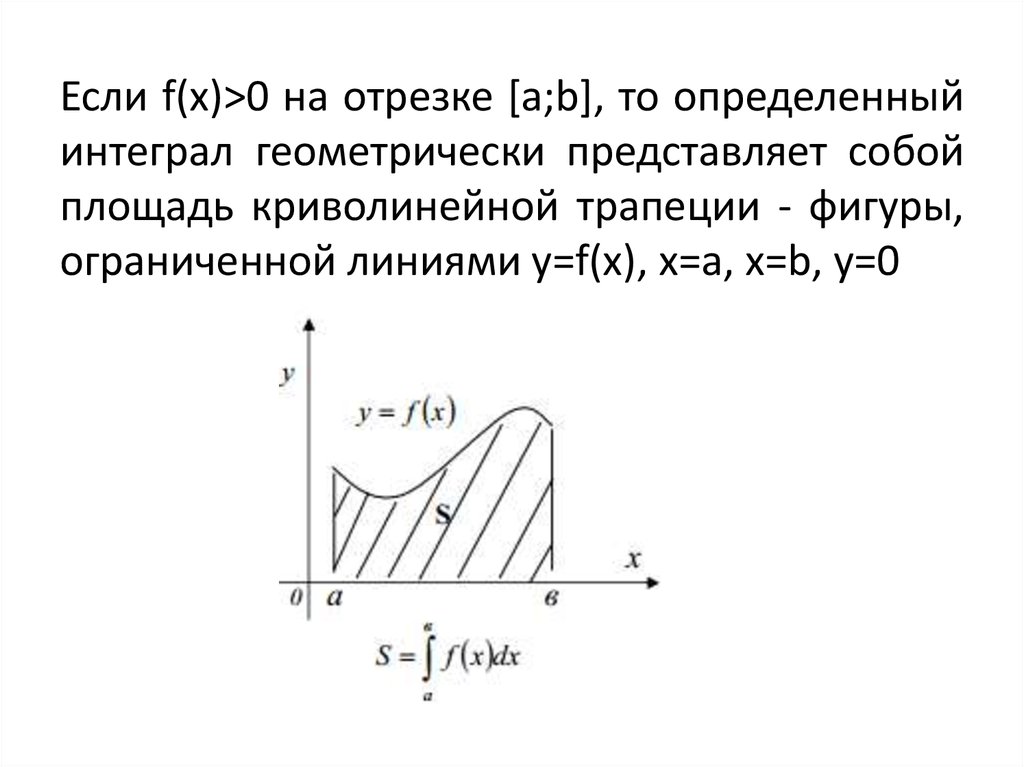
36.
Если f(x)>0 на отрезке [a;b], то определенныйинтеграл геометрически представляет собой
площадь криволинейной трапеции - фигуры,
ограниченной линиями у=f(x), x=a, x=b, y=0
37. Свойства определенного интеграла
38.
39. Правила вычисления определенных интегралов
1.Формула Ньютона-Лейбница:a
f ( x)dx F ( x)
a
b
F (b) F (a )
a
где F(x) – первообразная для f(x), т.е. F(x)‘= f(x).
2. Интегрирование по частям:
a
b
a
a
udv uv
a
vdu
a
где
u=u(x),
v=v(x)
–
непрерывно
дифференцируемые функции на отрезке [a;b].
40.
3. Замена переменнойa
f ( x)dx f (t ) (t )dt
a
где х=φ(t) – функция, непрерывная вместе со своей
производной φ‘ (t) на отрезке α≤t≤β, a= φ(a), b= φ(β),
f[φ(t)] – функция непрерывна на [α; β]
4. Если f(x) – нечетная функция, т.е. f(-x)=-f(x), то
a
f ( x)dx 0
a
Если f(x) –четная функция, т.е. f(-x)=f(x), то
.
a
а
a
0
f ( x)dx 2 f ( x)dx
41. Несобственные интегралы
Несобственными интегралами называются:1) интегралы с бесконечными пределами;
2) интегралы от неограниченных функций.
Несобственный интеграл от функции f(x) в пределах от а до +бесконечности
определяется равенством
b
f ( x)dx lim f ( x)dx
b
a
a
Если этот предел существует и конечен, то несобственный интеграл
называется сходящимся; если же предел не существует или равен
бесконечности, - расходящимися
b
b
b
a
a
b a
f ( x)dx lim f ( x)dx u f ( x)dx lim f ( x)dx
a
Если функция f(x) имеет бесконечный разрыв в точке с отрезка [a;b] и
непрерывна при а≤х<с и c<х≤b, то по определению полагают
.
c
b
b
f ( x)dx
f ( x)dx lim f ( x)dx lim
a
0
a
0
c
42.
При исследовании сходимости несобственных интеграловпользуются одним из признаков сравнения.
1. Если функции f(x) и φ(x) определены для всех х≥а и
интегрируемы на отрезке [a;А], где А≥а, и если 0≤f(x)≤φ(x) для
( x)dx вытекает
причем f ( x)dx ( x)dx
всех х≥а, то из сходимости интеграла
сходимость интеграла
f ( x)dx,
a
a
a
a
2.1 Если при х→+∞ функция f(x)≤0 является бесконечно малой
порядка р>0 по сравнению с 1/х, то интеграл
f ( x)dx
a
сходится при р>1 и расходится при р≤1.
2.2 Если функция f(x)≥0 определена и непрерывна в промежутке
а ≤ х<b и является бесконечно большой порядка р по сравнению с
b
1/(b-x) при х→b-0, то интеграл
f ( x)dx сходится при р<1 и
a
расходится при р ≥1.
43. Вычисление площади плоской фигуры
Площадь криволинейной трапеции, ограниченной кривой у=f(x) [f(x)≥0],прямыми x=a и x=b и отрезком [a;b] оси ОХ вычисляется по формуле
b
S f ( x)dx
a
Площадь фигуры, ограниченной кривой у=f1(x) и у=f2(x) [f1(x)≤f2(x)] и прямыми
x=a и x=b находится по формуле
b
S f1 ( x) f 2 ( x)dx
a
Если кривая задана параметрическими уравнениями х=х(t), у=у(t), то площадь
криволинейной трапеции, ограниченной этой кривой, прямыми x=a, x=b и
t2
отрезком [a;b] оси ОХ вычисляется по формуле
S y (t ) x (t )dt
t1
где t1 и t2 определяются из уравнения а=х(t1), b=х(t2) [y(t)≥0 при t1≤t≤t2]
Площадь криволинейного сектора, ограниченного кривой, заданной в
полярных координатах уравнением ρ=ρ(θ) и двумя полярными радиусами
θ=α, θ=β (α<β), находятся по формуле
1 2
S d
2
44. Вычисление длины дуги плоской кривой
Если кривая у=f(x) на отрезке [a;b] – гладкая (т.е. производнаяу’=f’(x) непрерывна), то длина соответствующей дуги этой кривой
b
находится по формуле
L
2
1 y dx
a
При параметрическом задании кривой х=х(t), у=у(t) [х(t) и у(t) –
непрерывно дифференцируемые функции] длина дуги кривой,
соответствующая, монотонному изменению параметра t от t1 до
t2
t2, вычисляется по формуле
L x 2 y 2 dt
t1
Если гладкая кривая задана в полярных координатах уравнением
ρ=ρ(θ), α≤θ≤β, то длина дуги равна
.
L 2 2 d
45. Вычисление объема тела
1. Вычисление объема тела по известным площадям поперечныхсечений. Если площадь сечения тела плоскость, перпендикулярной оси
ОХ, может быть выражена как функция от х, т.е. в виде S=S(х) (a≤x≤b),
объем части тела, заключенный между перпендикулярными оси ОХ
плоскостями x=a и x=b, находится по формуле
b
V S ( x)dx
a
2. Вычисление объема тела вращения. Если криволинейная трапеция,
ограниченная кривой у=f(x) и прямыми у=0, x=a, x=b, вращается вокруг
оси ОХ, то объем тела вращения вычисляется по формуле
b
Vх у 2 dx
a
Если фигура, ограниченная кривыми у1=f1(x) и у2=f2(x) [0≤f1(x)≤f2(x)] и
прямыми x=a, x=b, вращается вокруг оси ОХ, то объем тема вращения
b
равен
2
2
.
Vх у2 у1 dx
a
46. Вычисление площади поверхности вращения
Если дуга гладкой кривая у=f(x) (a≤х≤b) вращаетсявокруг оси ОХ, то площадь поверхности вращения
вычисляется по формуле
b
S х 2 у 1 y 2 dx
a
Если кривая задана параметрическими уравнениями
х=х(t), у=у(t) (t1≤t≤t2), то
t2
S х 2 у х 2 y 2 dt
.
t1
47. Обыкновенные дифференциальные уравнения
48. Основные понятия
• Дифференциальным уравнением называетсяуравнение,
связывающее
независимые
переменные, их функцию и производные (или
дифференциалы) этой функции.
• Если независимая переменная одна, то
уравнение называется обыкновенным, если
же независимых переменных две или больше,
то уравнение называется дифференциальным
уравнением в частных производных.
49. Уравнение первого порядка
Функциональное уравнение F(x,y,y ) = 0 или y = f(x,y),связывающее
между
собой
независимую
переменную, искомую функцию
y(x) и ее
производную y (x), называется дифференциальным
уравнением первого порядка.
Решением уравнения первого порядка называется
всякая функция y= (x), которая, будучи подставлена в
уравнение вместе со своей производной y = (x),
обращает его в тождество относительно x.
50. Общее решение дифференциального уравнения 1-го порядка
• Общим решением дифференциальногоуравнения первого порядка называется
такая функция y = (x,C), которая при
любом значении параметра C является
решением
этого
дифференциального
уравнения.
Уравнение
Ф(x,y,C)=0,
определяющее общее решение как
неявную функцию, называется общим
интегралом
дифференциального
уравнения.
51. Уравнение, разрешенное относительно производной
Если уравнение 1-го порядка разрешитьотносительно производной, то оно может
быть представлено в виде
y f ( x, y )
Его
общее
решение
геометрически
представляет
собой
семейство
интегральных кривых, т. е. совокупность
линий,
соответствующих
различным
значениям постоянной C.
52. Постановка задачи Коши
Задачаотыскания
решения
дифференциального уравнения y f ( x, y ) ,
удовлетворяющего начальному условию y y 0
при x x0 ,называется задачей Коши для
уравнения 1-го порядка.
Геометрически
это
означает:
найти
интегральную кривую дифференциального
уравнения y f ( x, y ) , проходящую через
данную точку M 0 ( x0 , y0 ) .
53. Уравнение с разделяющимися переменными
Дифференциальное уравнениеf ( x)dx g ( y )dy
называется
уравнением
с
разделенными
переменными.
Дифференциальное уравнение 1-го порядка
называется уравнением с разделяющимися
переменными, если оно имеет вид:
M1 ( x ) N1 ( y )dx M 2 ( x ) N 2 ( y )dy 0
Для решения уравнения делят обе его части на
N1 ( y)M 2 ( x) , а затем
произведение функций
интегрируют.
54. Однородные уравнения
Дифференциальное уравнение первогопорядка называется однородным, если его
y
можно привести к виду y = f ( )
x
или к виду M ( x , y )dx N ( x , y )dy 0
где M ( x, y ) и N ( x , y ) – однородные
функции одного порядка .
55. Линейные уравнения 1-го порядка
Дифференциальное уравнение первого порядканазывается линейным, если оно содержит у
и у‘ в первой степени, т.е. имеет вид
y P( x ) y . Q( x )
Решают
такое
уравнение
с
помощью
подстановки y=uv, где u и v-вспомогательные
неизвестные функции, которые находят,
подставляя в уравнение вспомогательные
функции и на одну из функций налагают
определенные условия.
56. Уравнение Бернулли
Уравнением Бернулли называетсяуравнение 1-го порядка, имеющее вид
m
y P( x ) y Q,( x ) y
где m 0 и m 1
Его, как и линейное уравнение решают с
помощью подстановки
y uv
57. Дифференциальные уравнения 2-го порядка
Уравнение 2-го порядка имеет видF(x,y,y ,y ) 0
Или
y f ( x, y , y )
Общим решением уравнения второго порядка
называется такая функция y ( x , c1 , c2 ) ,
которая при любых значениях параметров c1 ,c2
является решением этого уравнения.
58. Задача Коши для уравнения 2-го порядка
Если уравнение 2-го порядка разрешитьотносительно второй производной, то для такого
уравнения имеет место задача: найти решение
уравнения y f ( x, y, y ),
удовлетворяющее начальным условиям:
y( x0 ) y0 и y ( x0 ) y 0
Эту задачу называют задачей Коши для
дифференциального уравнения 2-гопорядка.
59. Теорема существования и единственности решения уравнения 2-го порядка
Если в уравнении y f ( x, y, y ) функцияf ( x, y, y ) и ее частные производные по
аргументам y и y непрерывны в
некоторой области, содержащей
точку ( x0 , y 0 , y 0 ) , то существует и притом
единственное решение y y (x ) этого
уравнения, удовлетворяющее условиям
y( x0 ) y0 и y ( x0 ) y0 .
60. Уравнения 2-го порядка, допускающие понижение порядка
Простейшее уравнение 2-го порядкаy f ( x ) решают двукратным
интегрированием.
Уравнение F ( x , y , y ), 0 не содержащее
явно у, решают с помощью подстановки
y p , y p
Уравнение F ( y , y , y ,) 0 не содержащее х,
решают заменой
dp
p.
y p ,
y
dy
61. Линейные однородные уравнения
Линейным однороднымдифференциальным уравнением второго
порядка называется уравнение
y p( x ) y q( x ) y 0
Если все коэффициенты этого уравнения
постоянны, то уравнение называется
уравнением с постоянными
коэффициентами .
62. Свойства решений линейного однородного уравнения
Теорема 1. Если у(х) являетсярешением уравнения , то и Су(х), где Сконстанта, также является решением
этого уравнения.
63. Свойства решений линейного однородного уравнения
Теорема 2. Если y1 ( x) и y2 ( x) -решенияуравнения, то и их сумма также
является решением этого уравнения.
Следствие. Если y1 ( x) и y2 ( x) -решения
уравнения, то функция
y C1 y1 C2 y2
-также решение этого уравнения.
64. Линейно зависимые и линейно независимые функции
Две функции y1 ( x) и y2 ( x) называютсялинейно зависимыми на некотором
промежутке, если можно подобрать такие
числа и ,не равные нулю
одновременно, что линейная комбинация
этих функций тождественно равна нулю на
этом промежутке, т. е.
y1 y2 0
65.
Если таких чисел подобрать нельзя, тофункции y1 ( x) и y2 ( x) называются линейно
независимыми на указанном промежутке.
Функции y1 ( x) и y2 ( x) будут линейно
зависимыми тогда и только тогда, когда их
отношение постоянно, т. е.
y1 ( x)
k
y 2 ( x)
66. Теорема о структуре общего решения линейного однородного уравнения 2-го порядка
Теорема о структуре общего решениялинейного однородного уравнения 2-го
Если y ( x) и y (порядка
x) -линейно независимые
1
2
частные решения ЛОУ 2-го порядка, то их
линейная комбинация
y C1 y1 C2 y2
где C1 и C2 -произвольные постоянные,
является общим решением этого
уравнения.
67. Линейное однородное уравнение 2-го порядка с постоянными коэффициентами
Уравнение k 2 pk q 0 называетсяхарактеристическим уравнением
линейного уравнения y py qy 0 .
Оно получается из ЛОУ заменой
соотстветствующей порядку производной
степенью k .



































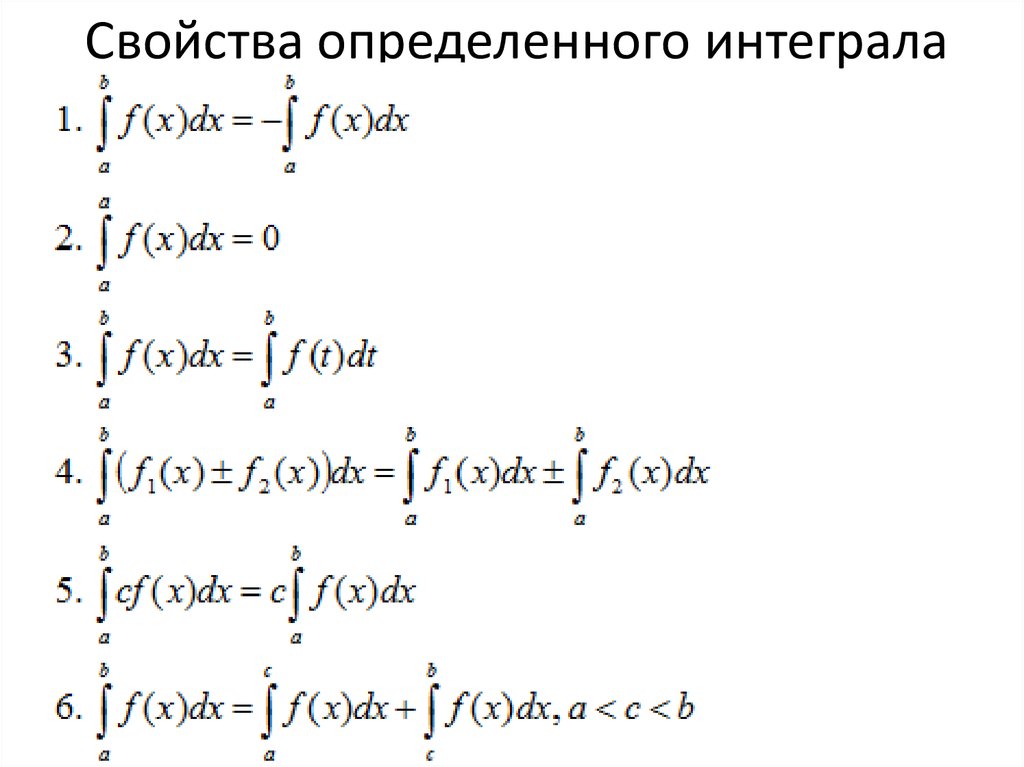






























 Математика
Математика








