Похожие презентации:
Полезные факты и теоремы
1.
Государственное бюджетноеобщеобразовательное
учреждение
средняя общеобразовательная
школа № 254
с углубленным изучением
английского языка
Кировского района
Лекции профессора А.Г. Мордковича
в пересказе учителя математики
Павловой Марины Константиновны
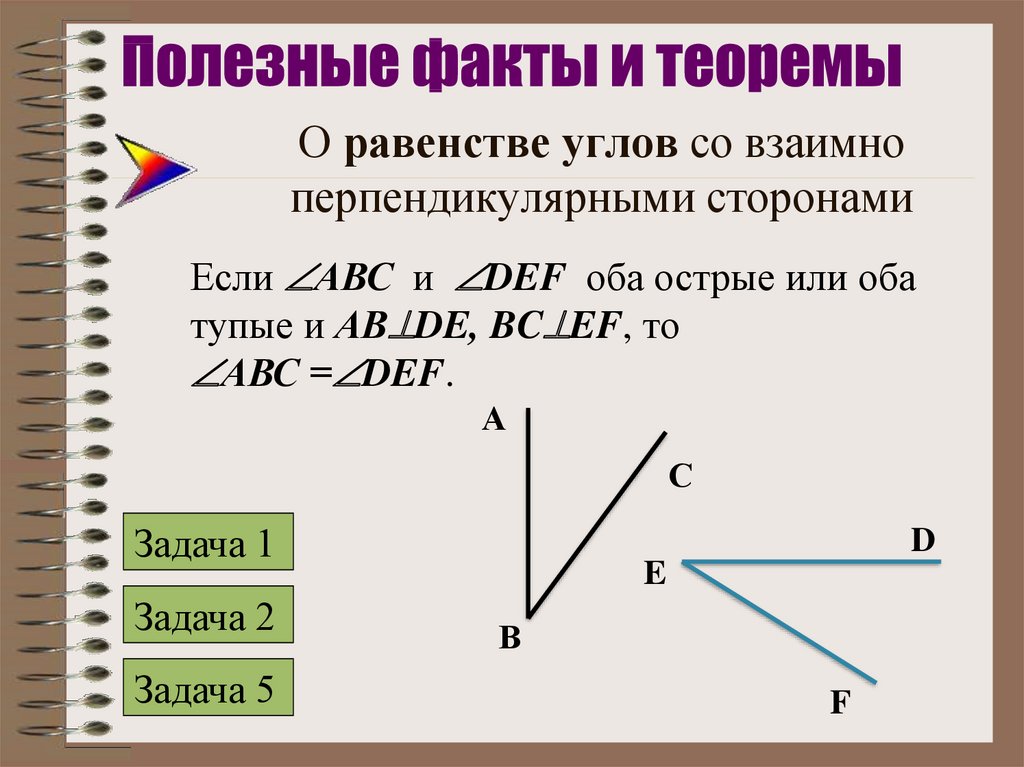
2. О равенстве углов со взаимно перпендикулярными сторонами
Если АВС и DEF оба острые или обатупые и АВ DE, BC EF, то
АВС = DEF.
А
С
Задача 1
Задача 2
Задача 5
D
E
В
F
3. О точках пересечения медиан, биссектрис, высот треугольника
Три биссектрисы треугольника пересекаютсяв одной точке.
Три высоты треугольника пересекаются в
одной точке (ортоцентр треугольника).
Три медианы треугольника пересекаются в
одной точке (центроид треугольника) и
делятся ею в отношении 2:1, считая от
вершины.
Задача 4
4. Свойства средней линии трапеции
Средняя линия параллельна основаниямтрапеции.
Средняя линия равна полусумме оснований
трапеции.
Средняя линия (и только она) делит пополам
любой отрезок, заключенный между
основаниями трапеции.
Эти теоремы справедливы и для средней
линии треугольника.
Задача 6
5. Свойство медианы в прямоугольном треугольнике
В прямоугольном треугольнике медиана,проведенная к гипотенузе, равна ее половине.
Обратная теорема
Если в треугольнике одна из медиан равна
половине стороны, к которой она проведена,
то этот треугольник прямоугольный.
Задача 5
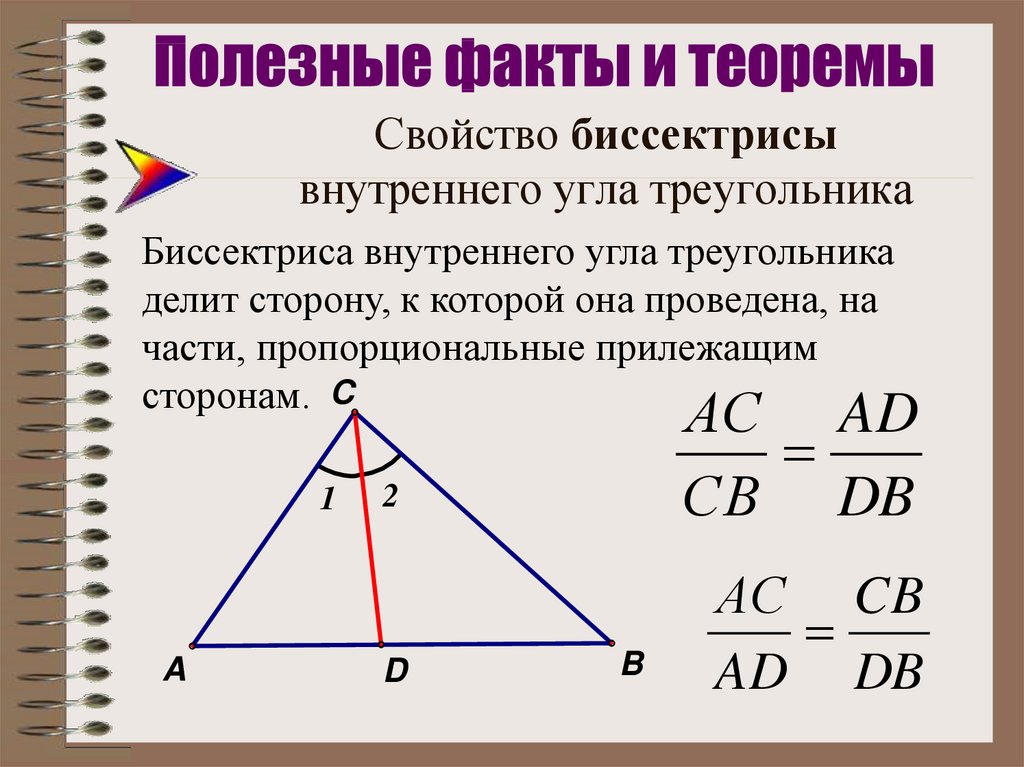
6. Свойство биссектрисы внутреннего угла треугольника
Биссектриса внутреннего угла треугольникаделит сторону, к которой она проведена, на
части, пропорциональные прилежащим
сторонам. C
1
A
2
АС AD
СВ DB
D
АС CB
AD DB
B
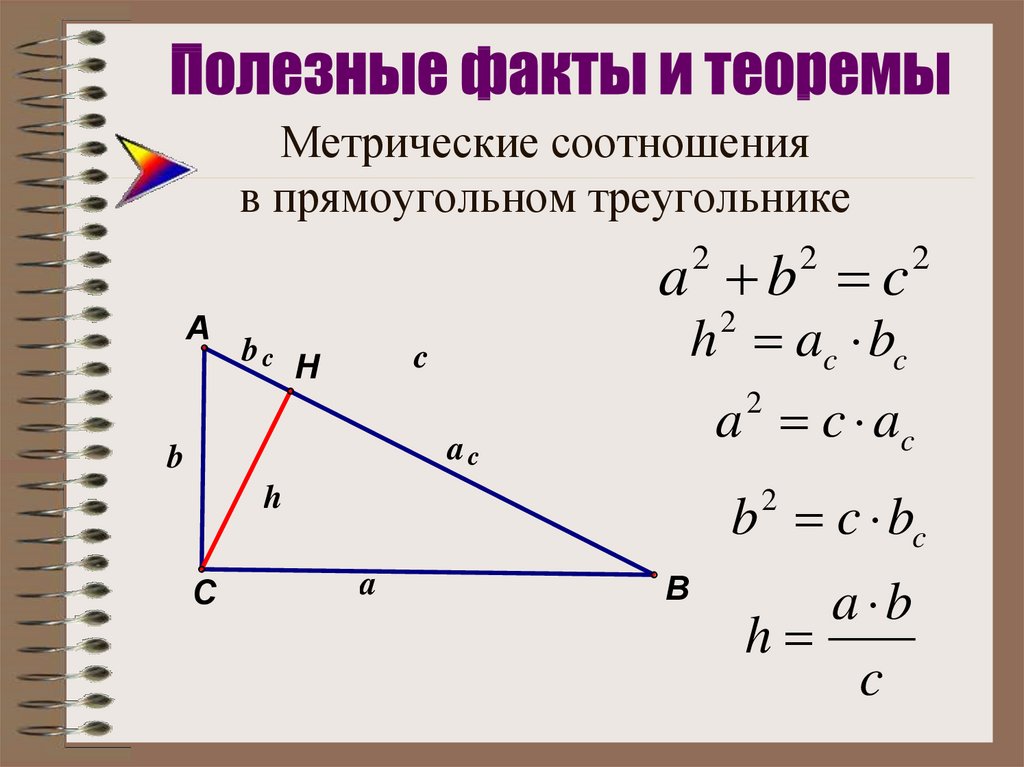
7. Метрические соотношения в прямоугольном треугольнике
a b c2
А
bc
2
2
h ac bc
2
c
H
a c ac
2
ac
b
b c bc
h
С
2
a
В
a b
h
c
8. Определение вида треугольника по его сторонам
Пусть а, b и с – стороны треугольника,причем с - наибольшая сторона, тогда
если с² < а² + b², то
треугольник остроугольный
b
а
с
Задача 9
если с² = а² + b², то
треугольник прямоугольный
если с² > а² + b², то
треугольник тупоугольный
9. Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
Метрические соотношения в параллелограммеСумма квадратов диагоналей параллелограмма
равна сумме квадратов всех его сторон:
d d 2a 2b
2
1
2
2
2
а
B
C
d2
b
b
d1
Задача 3
A
а
D
2
10. Если два треугольника подобны, то любой линейный элемент (или сумма линейных элементов) одного треугольника относится к
Обобщенная теорема подобияЕсли два треугольника подобны, то любой
линейный элемент (или сумма линейных
элементов) одного треугольника относится к
соответствующему линейному элементу (или
сумме соответствующих линейных элементов)
другого треугольника как соответственные
стороны.
Соответственные
линейные
элементы:
медианы, высоты, биссектрисы, периметры,
радиусы описанной и вписанной окружностей.
Задача 9
11.
Рассмотреть эти отрезки как стороны двухтреугольников и доказать, что треугольники
равны.
Рассмотреть эти отрезки как стороны одного
треугольника и доказать, что треугольник
равнобедренный.
Заменить отрезок а равным отрезком а1 ,
отрезок b равным отрезком b1 и доказать
равенство отрезков а1 и b1.
12.
Проведение прямой, параллельной илиперпендикулярной одной из имеющихся.
Удвоение медианы треугольника с целью
достроить треугольник до параллелограмма.
Проведение вспомогательной биссектрисы.
Дополнительные построения, связанные с
окружностью.
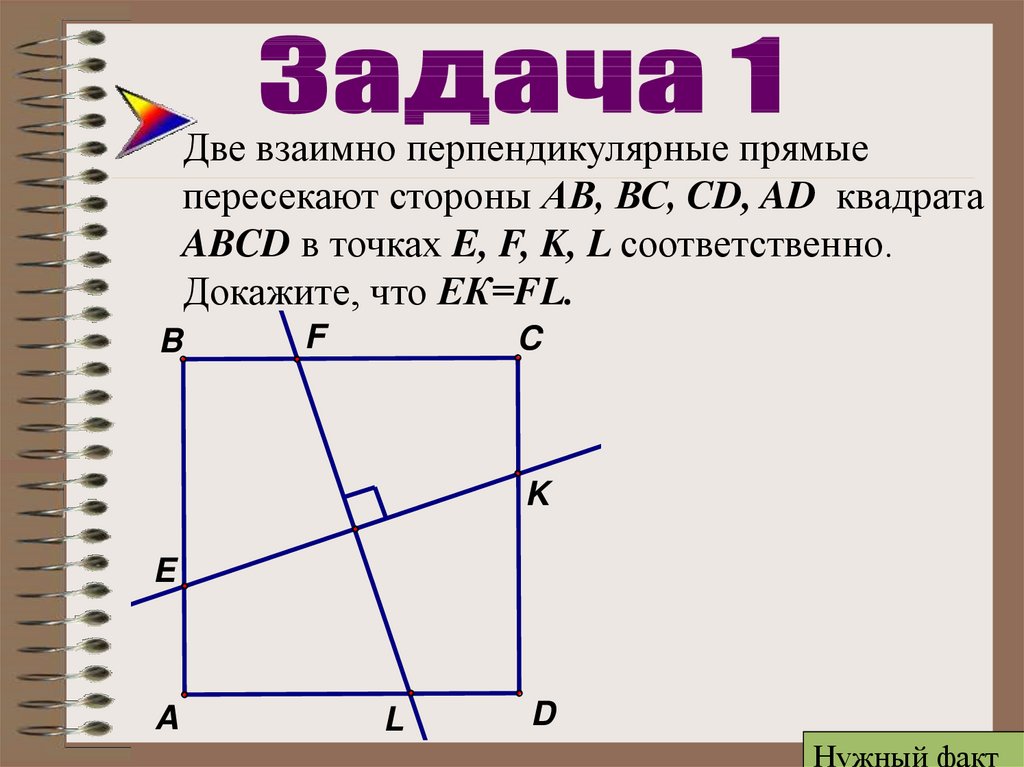
13.
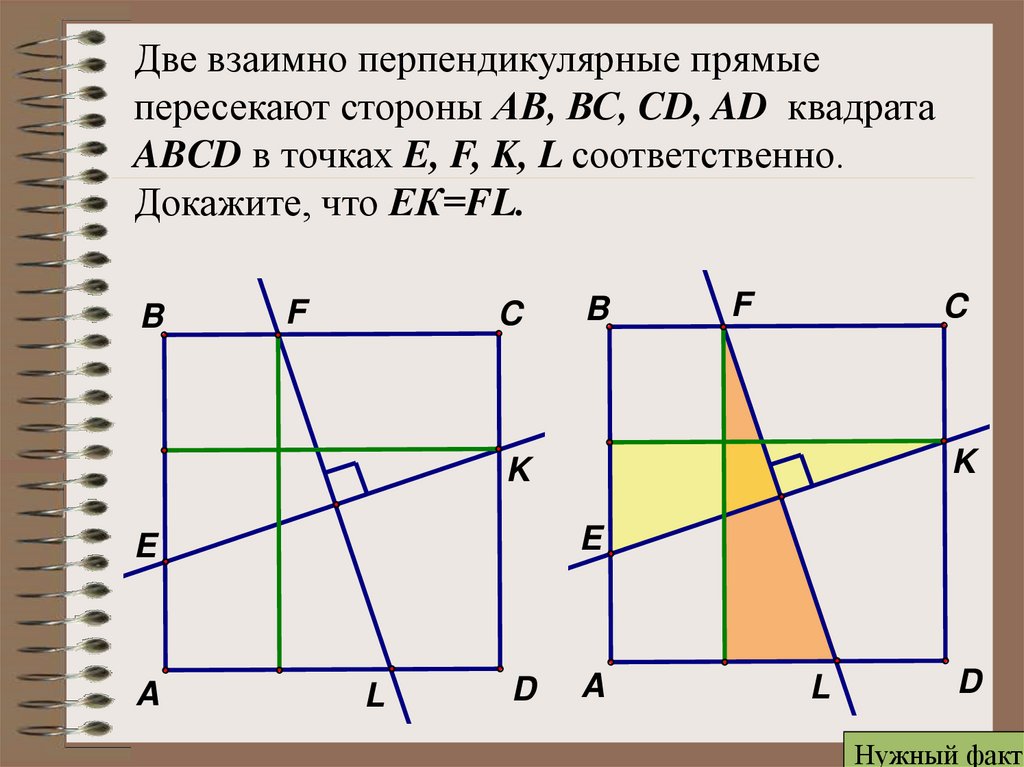
Две взаимно перпендикулярные прямыепересекают стороны АВ, ВС, CD, AD квадрата
ABCD в точках E, F, K, L соответственно.
Докажите, что ЕК=FL.
B
F
C
K
E
A
L
D
Нужный факт
14.
Две взаимно перпендикулярные прямыепересекают стороны АВ, ВС, CD, AD квадрата
ABCD в точках E, F, K, L соответственно.
Докажите, что ЕК=FL.
B
F
C
B
F
C
K
K
E
E
A
L
D A
L
D
Нужный факт
15.
Две взаимно перпендикулярные прямыепересекают стороны АВ, ВС, CD, AD квадрата
ABCD в точках E, F, K, L соответственно.
Докажите, что ЕК=FL.
B
F
C
B
F
C
K
K
E
E
A
L
D
A
L
D
Нужный факт
16.
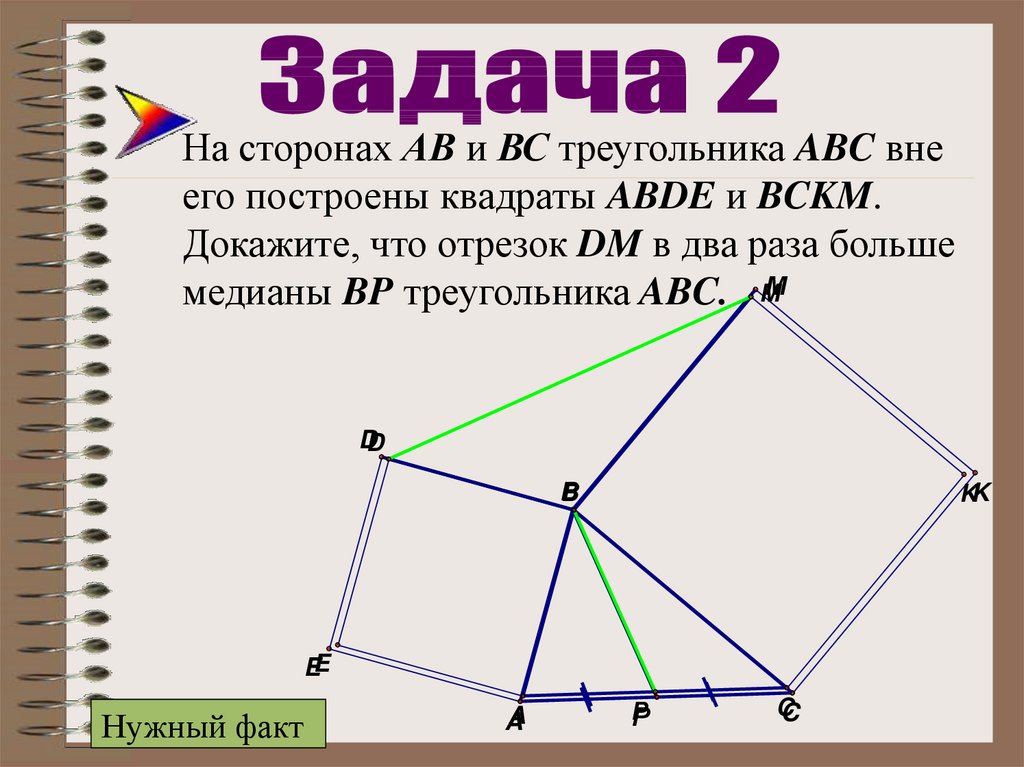
На сторонах АВ и ВС треугольника ABC внеего построены квадраты ABDE и BCKM.
Докажите, что отрезок DM в два раза больше
медианы BP треугольника ABC. MM
DD
B
KK
EE
Нужный факт
A
A
Р
Р
C
C
17.
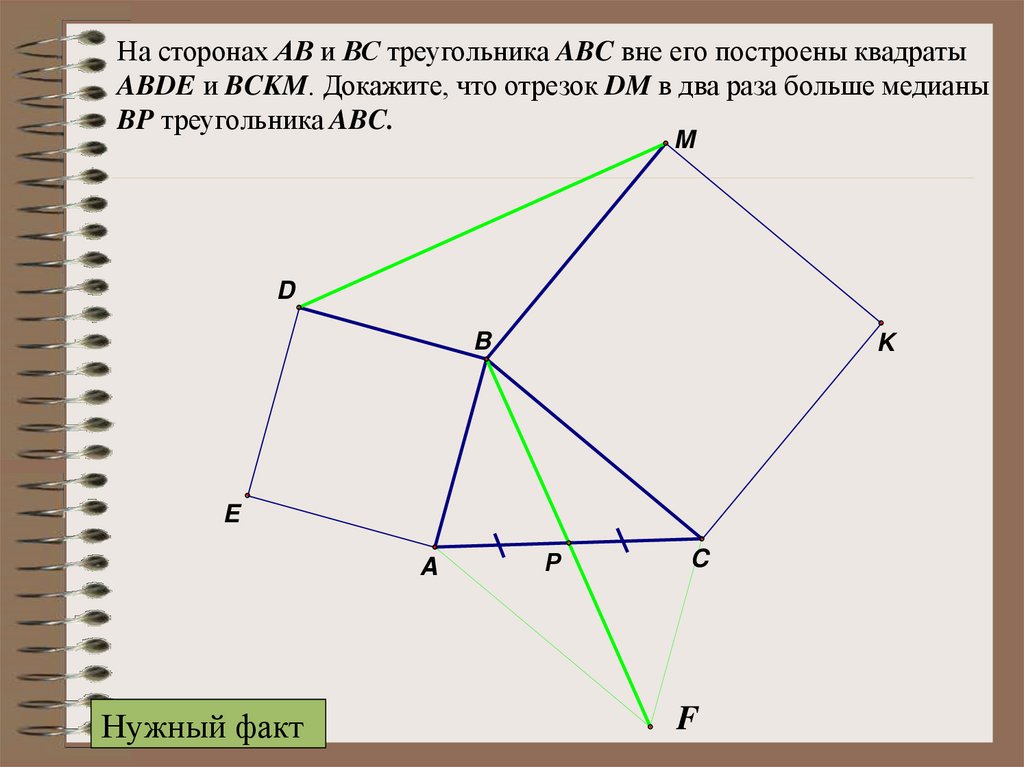
На сторонах АВ и ВС треугольника ABC вне его построены квадратыABDE и BCKM. Докажите, что отрезок DM в два раза больше медианы
BP треугольника ABC.
M
D
B
K
E
A
Нужный факт
Р
C
F
18.
Стороны треугольника а, b, c. Вычислитьмедиану mc, проведенную к стороне с.
C
C
a
b
a
b
mc
A
c
mc
B A
B
c
a
Нужный факт
b
P
19.
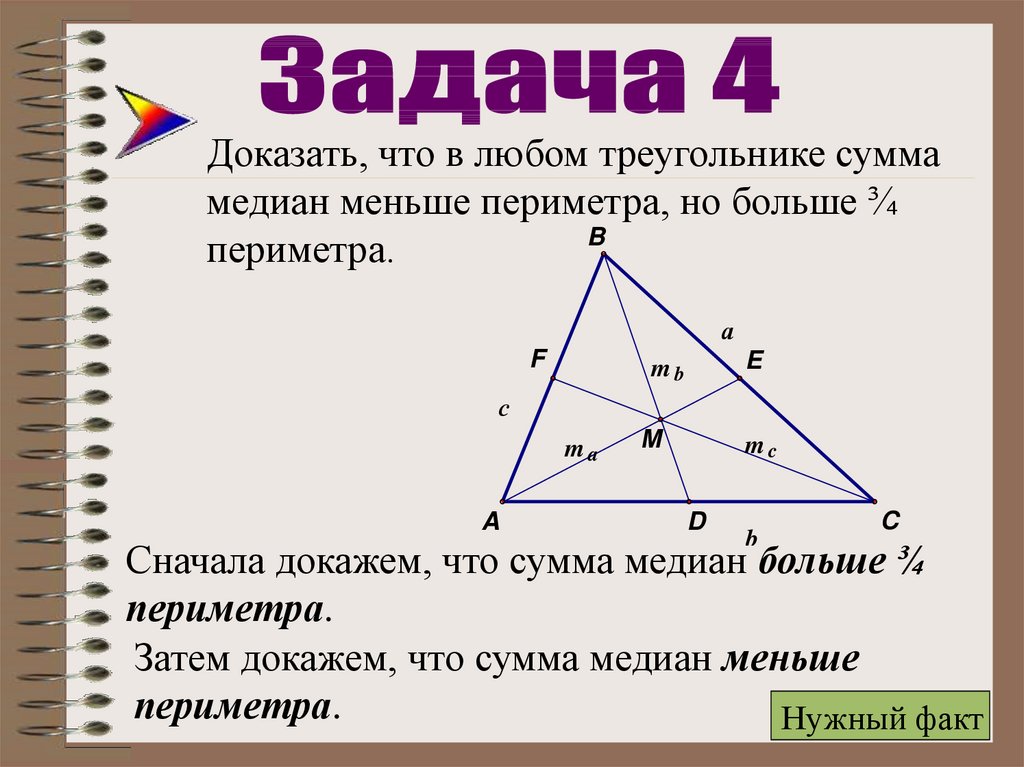
Доказать, что в любом треугольнике суммамедиан меньше периметра, но больше ¾
B
периметра.
а
F
E
mb
с
ma
A
М
mc
D
b
C
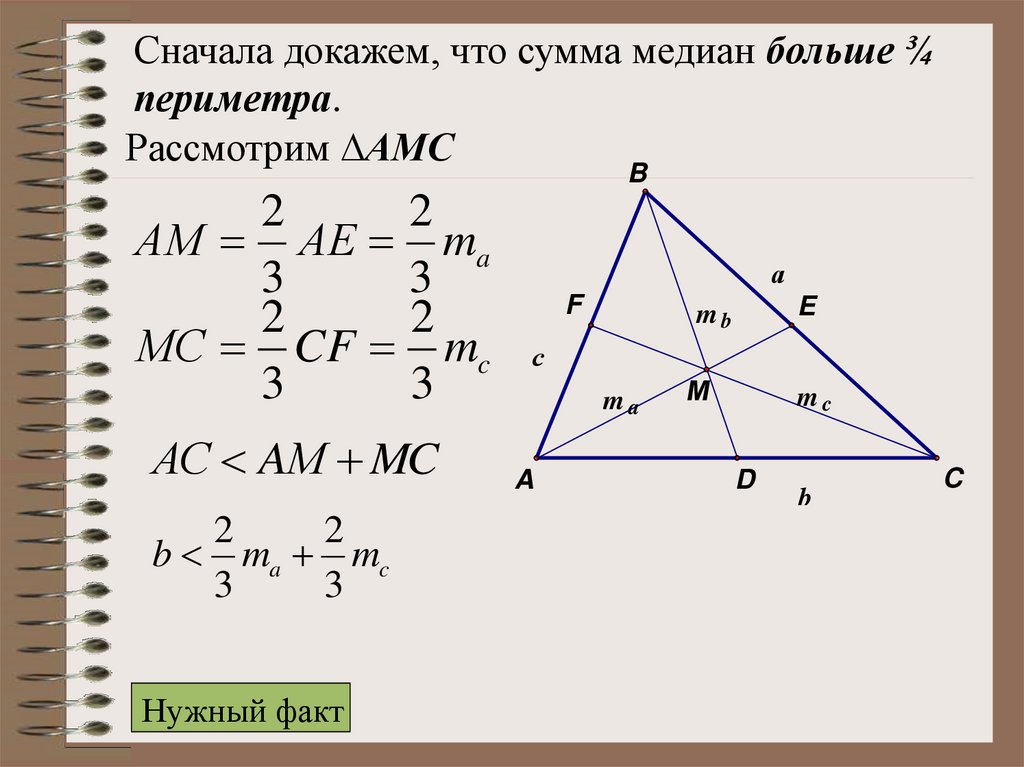
Сначала докажем, что сумма медиан больше ¾
периметра.
Затем докажем, что сумма медиан меньше
периметра.
Нужный факт
20.
Сначала докажем, что сумма медиан больше ¾периметра.
Рассмотрим АМС
B
2
2
АМ АЕ ma
3
3
2
2
МC CF mc
3
3
АC AМ MC
2
2
b ma mc
3
3
Нужный факт
а
F
E
mb
с
ma
A
М
mc
D
b
C
21.
Рассмотрим BМС: BC BМ MC2
2
a mb mc
3
3
Рассмотрим ABМ: AB BМ AM
2
2
B
c mb ma
3
3
2
2
2
a b c 2 ( ma mb mc )
3
3
3 F
mb
4
a b c (ma mb mc ) с
3
М
ma
3
(a b c) ma mb mc
4
A
D
3
ma mb mc (a b c)
4
а
E
mc
b
C
22.
Докажем, что сумма медиан меньше периметра.B
B
Рассмотрим BСК:
BК BС CК
2mb a c
2ma b c
2mc a b
аа
F
F
mbb
m
сс
m aa
m
A
М
М
EE
mcc
m
D
D
bb
2(ma mb mc ) 2(a b c)
ma mb mc a b c
К
CC
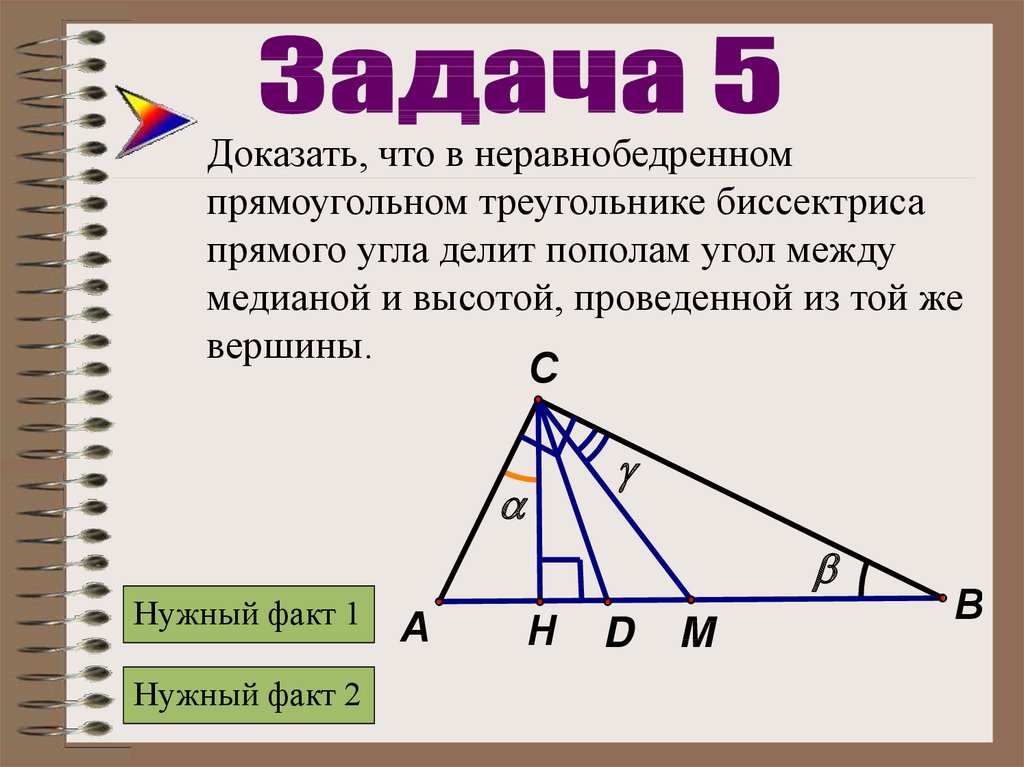
23.
Доказать, что в неравнобедренномпрямоугольном треугольнике биссектриса
прямого угла делит пополам угол между
медианой и высотой, проведенной из той же
вершины.
С
Нужный факт 1
Нужный факт 2
А
Н
D
M
В
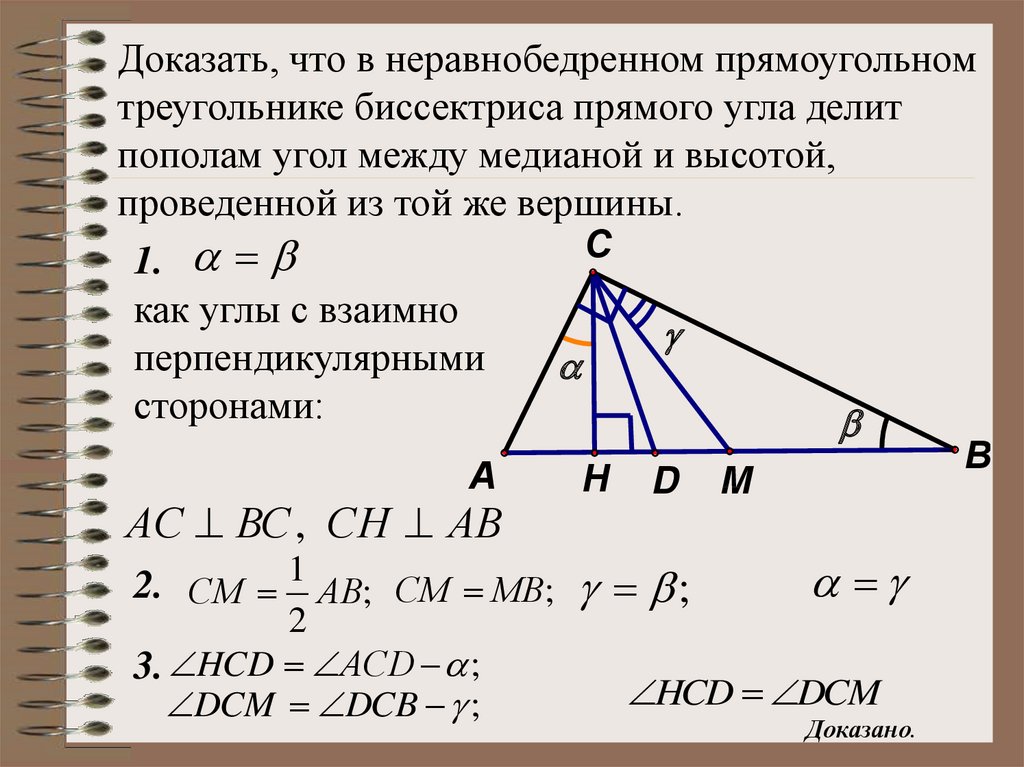
24.
Доказать, что в неравнобедренном прямоугольномтреугольнике биссектриса прямого угла делит
пополам угол между медианой и высотой,
проведенной из той же вершины.
С
1.
как углы с взаимно
перпендикулярными
сторонами:
А
АС ВС , СН АВ
Н
D
2. СМ 1 АВ; СМ МВ; ;
2
3. HCD АCD ;
DCM DCB ;
В
M
HCD DCM
Доказано.
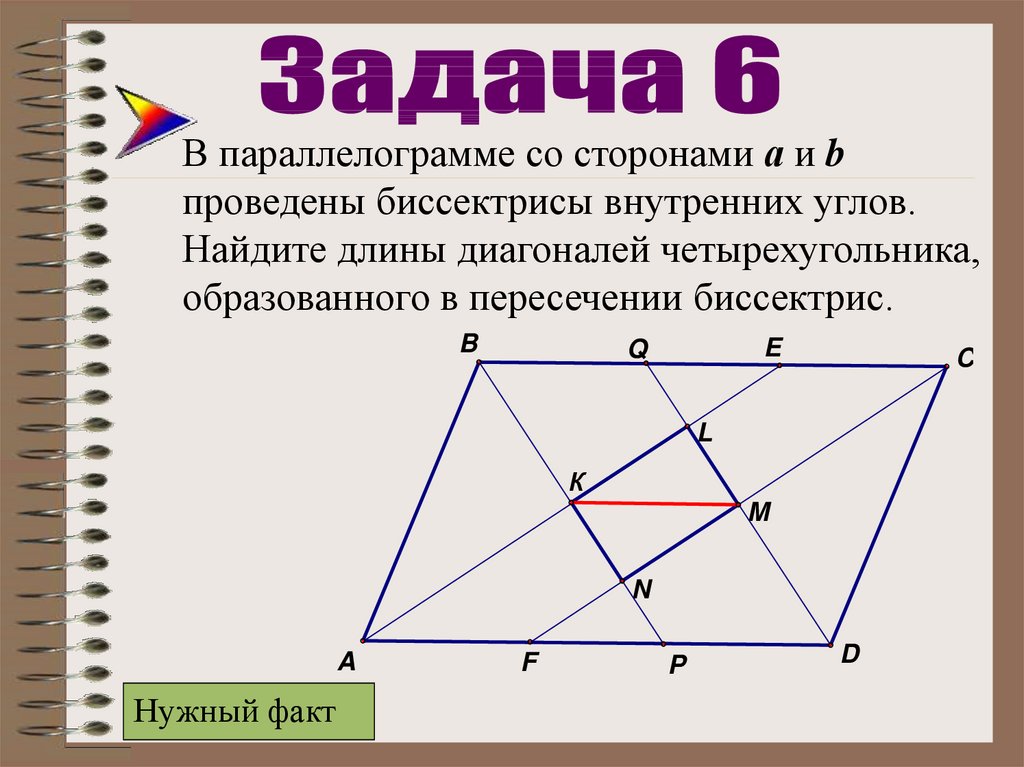
25.
В параллелограмме со сторонами а и bпроведены биссектрисы внутренних углов.
Найдите длины диагоналей четырехугольника,
образованного в пересечении биссектрис.
B
E
Q
C
L
К
M
N
A
Нужный факт
F
P
D
26.
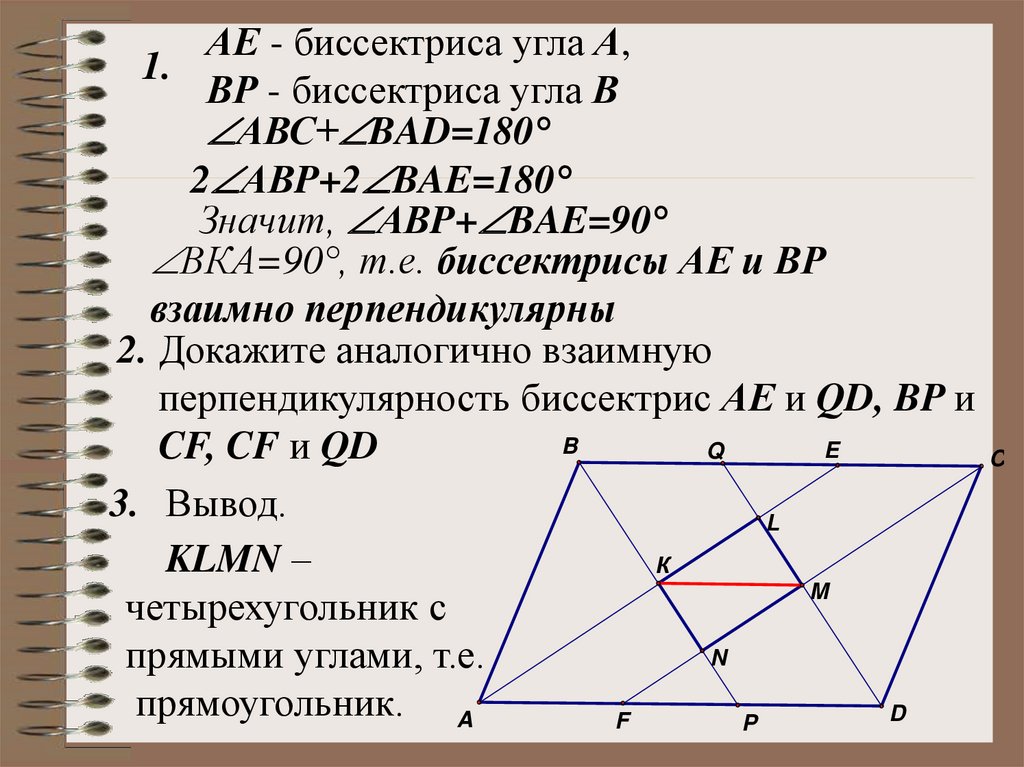
АЕ - биссектриса угла А,1.
ВР - биссектриса угла В
АВС+ BAD=180°
2 АВP+2 BAE=180°
Значит, АВP+ BAE=90°
ВКА=90°, т.е. биссектрисы АЕ и ВР
взаимно перпендикулярны
2. Докажите аналогично взаимную
перпендикулярность биссектрис АЕ и QD, BP и
B
E
CF, CF и QD
Q
3. Вывод.
L
KLMN –
К
M
четырехугольник с
N
прямыми углами, т.е.
прямоугольник. A
D
F
P
C
27.
4. Так как KLMN – прямоугольник, достаточнонайти длину KM.
5. Рассмотрим АВР.
АК – биссектриса и высота, значит АВР –
равнобедренный и АК – медиана.
6. АВ=АP = b, К – середина ВР.
Аналогично, М – середина QD.
B
E
Q
C
7. КМ делит пополам
отрезки BP и QD.
L
К
Значит КМ - отрезок
M
на средней линии
N
параллелограмма,
D
F
P
поэтому КМ AD. A
8. KMDP – параллелограмм, KM=PD = AD-AP =a-b
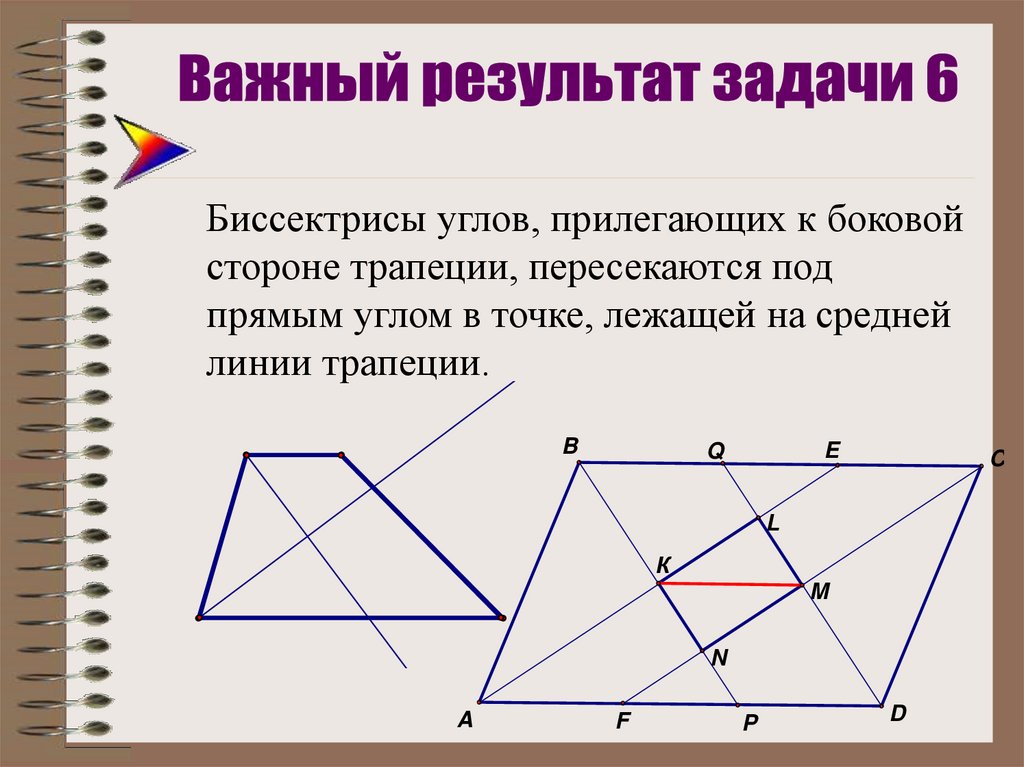
28.
Биссектрисы углов, прилегающих к боковойстороне трапеции, пересекаются под
прямым углом в точке, лежащей на средней
линии трапеции.
B
E
Q
C
L
К
M
N
A
F
P
D
29.
Основным методом составления уравнений вгеометрических задачах является метод
опорного элемента.
Он заключается в том, что один и тот же элемент
(сторона, угол, площадь, радиус и т.д.)
выражается через известные и неизвестные
величины двумя различными способами и
полученные выражения приравниваются.
В качестве опорного элемента часто выбирается
площадь фигуры. Тогда говорят, что используется
метод площадей.
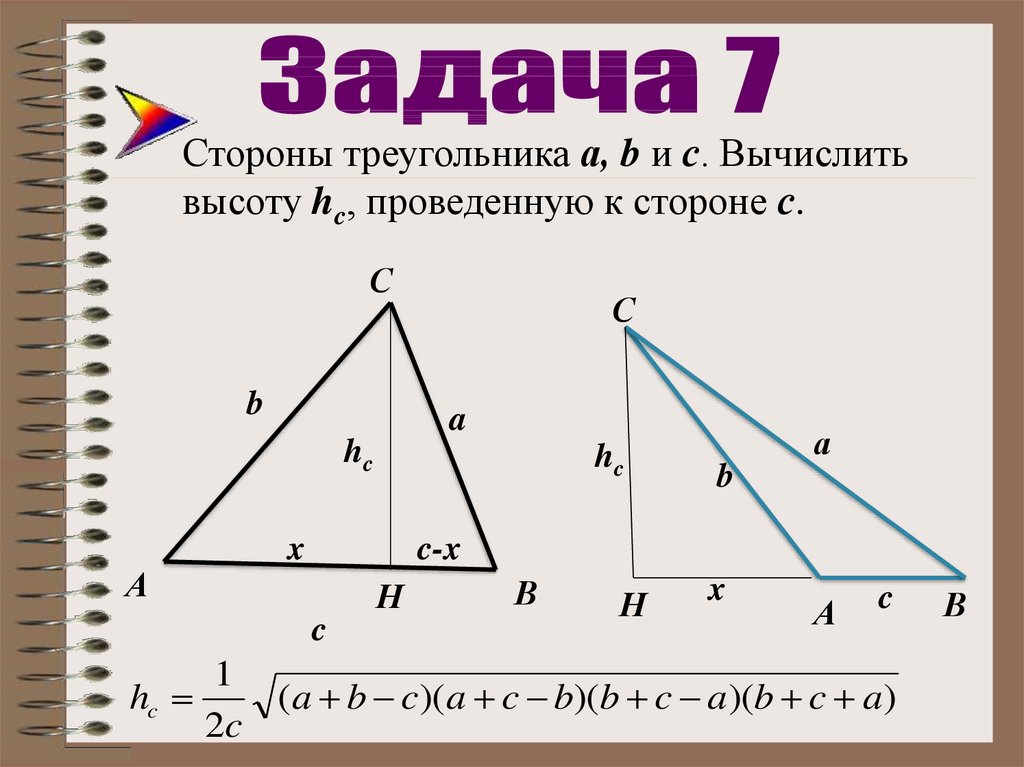
30.
Стороны треугольника а, b и с. Вычислитьвысоту hc, проведенную к стороне с.
С
b
С
a
hc
А
hc
x
а
b
c-x
Н
c
В
Н
x
А
c
1
hc
(a b c)( a c b)(b c a)(b c a)
2c
В
31.
Если в задаче требуется найти отношениекаких-либо величин, то она решается методом
введения вспомогательного параметра.
В начале решения задачи какая-либо линейная
величина принимается как известная.
Обозначив ее буквой а, выражаем через нее те
величины, отношение которых требуется найти.
Тогда при составлении искомого отношения
вспомогательный параметр а сократится.
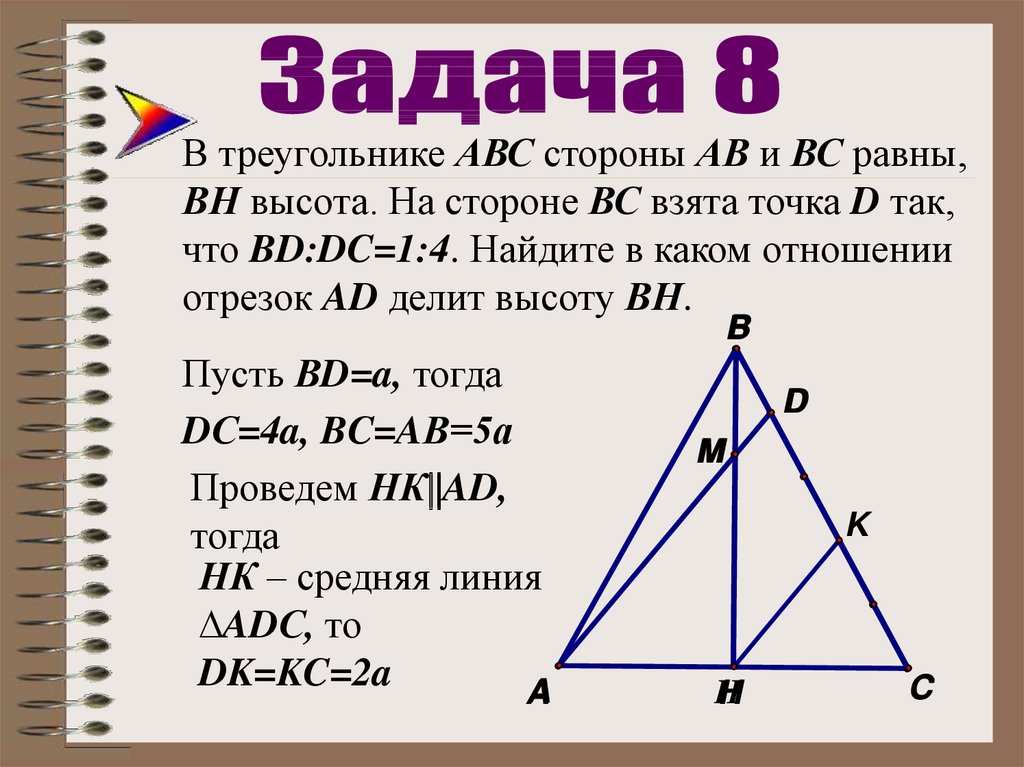
32.
В треугольнике АВС стороны АВ и ВС равны,ВН высота. На стороне ВС взята точка D так,
что BD:DC=1:4. Найдите в каком отношении
отрезок AD делит высоту ВН.
B
Пусть ВD=a, тогда
DС=4a, BC=AВ=5а
Проведем НК AD,
тогда
НК – средняя линия
ADС, то
DK=KC=2a
A
D
M
K
H
C
33.
В треугольнике АВС стороны АВ и ВС равны, ВНвысота. На стороне ВС взята точка D так, что
BD:DC=1:4. Найдите в каком отношении отрезок
AD делит высоту ВН.
В ВНК по теореме Фалеса
ВМ BD
МН DK
BD
a
DK 2a
BD 1
DK 2
A
BM 1
MH 2
B
D
M
K
H
C
34.
В треугольник со сторонами 10, 17 и 21 см,вписан прямоугольник так, что две его вершины
находятся на одной стороне треугольника, а две
вершины - на двух других сторонах
треугольника. Найти стороны прямоугольника,
если известно, что его периметр равен 22,5 см.
B
Определим вид
треугольника.
212 ? 102 17 2
Значит, треугольник
тупоугольный.
Нужный факт
A
H
C
35.
В треугольник со сторонами 10, 17 и 21 см, вписан прямоугольниктак, что две его вершины находятся на одной стороне треугольника,
а две вершины - на двух других сторонах треугольника. Найти
стороны прямоугольника, если известно, что его периметр равен
22,5 см.
Тогда две вершины прямоугольника лежат на
большей стороне треугольника.
Найдем высоту ВН как в задаче 7.
B
B
ВН=8 см
Пусть ЕD=х, тогда
EF=11,25-x,
P
F
E
ВР=8-x
A
H
D H
K
C
C
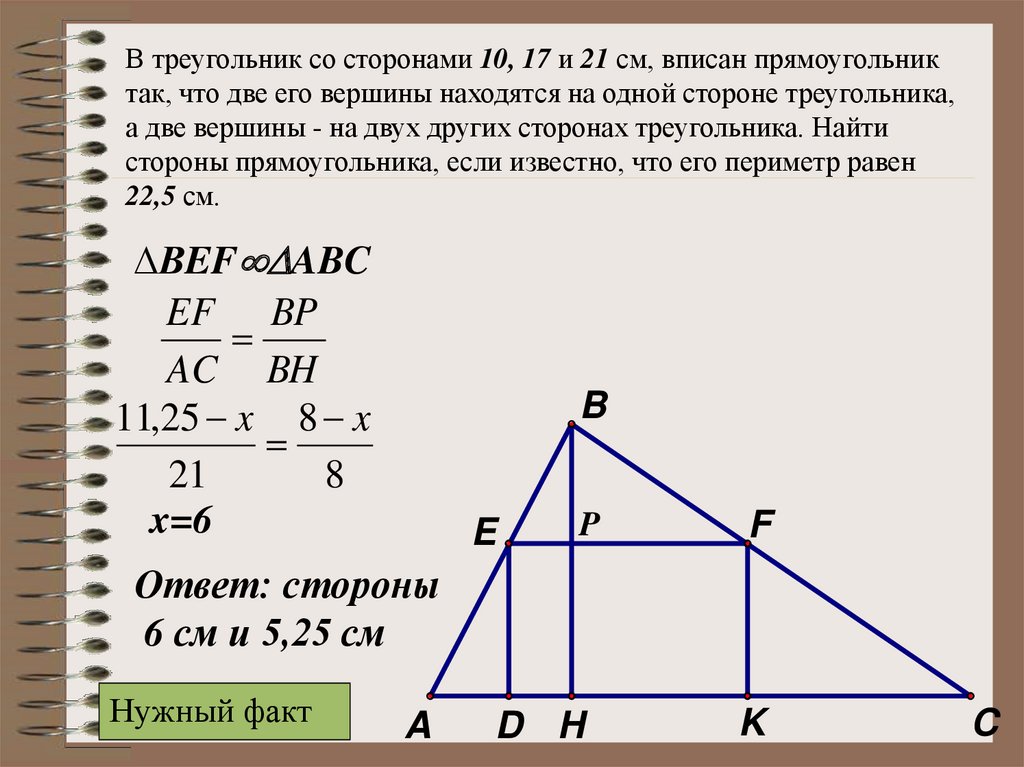
36.
В треугольник со сторонами 10, 17 и 21 см, вписан прямоугольниктак, что две его вершины находятся на одной стороне треугольника,
а две вершины - на двух других сторонах треугольника. Найти
стороны прямоугольника, если известно, что его периметр равен
22,5 см.
ВEF ABC
EF BP
AC BH
11,25 x 8 x
21
8
x=6
B
E
P
F
Ответ: стороны
6 см и 5,25 см
Нужный факт
A
D H
K
C
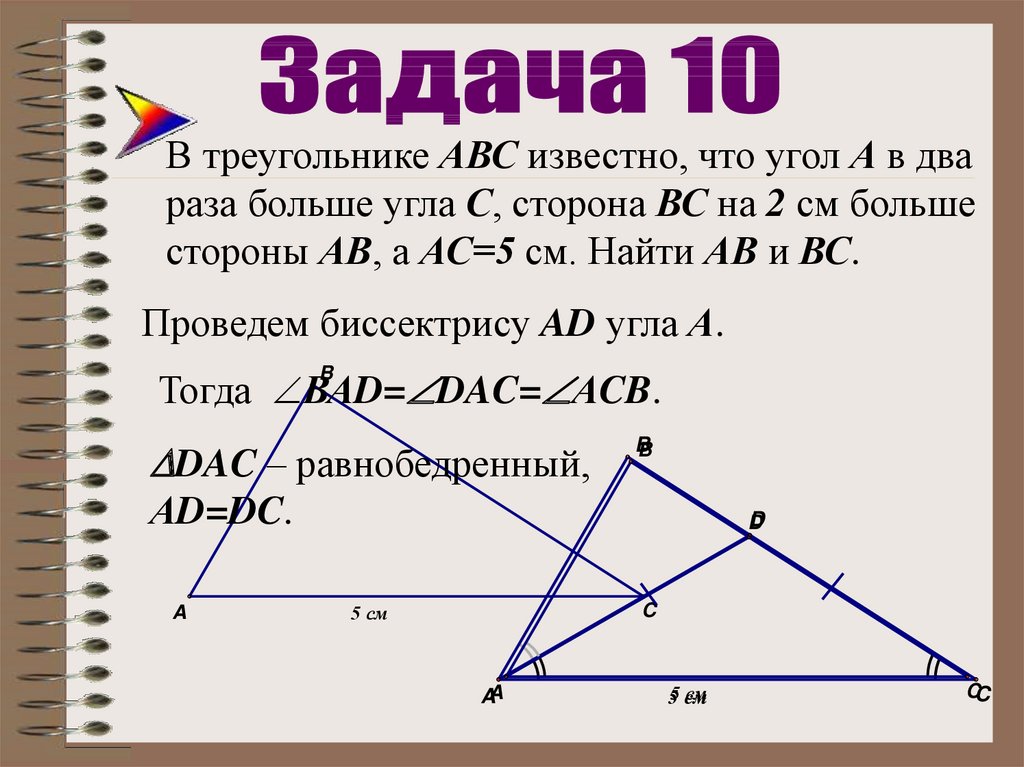
37.
В треугольнике АВС известно, что угол А в двараза больше угла С, сторона ВС на 2 см больше
стороны АВ, а АС=5 см. Найти АВ и ВС.
Проведем биссектрису AD угла А.
Тогда ВАD= DAC= АCB.
B
DAC – равнобедренный,
B
B
АD=DC.
A
D
5 см
C
AA
5 см
CC
38.
В треугольнике АВС известно, что угол А в два разабольше угла С, сторона ВС на 2 см больше стороны АВ, а
АС=5 см. Найти АВ и ВС.
Т.к. ВАD= ВСA, B – общий, то АВD ABC
B
АВ BD AD
ВС AB AC
х+2-у
D
х
x
x 2 y y
x 2
x
5
y
x
x 2 5 ,
x 2 y y
x
5
5 x xy 2 y,
5 x 10 5 y xy
у
у
5 см
A
5 y 10 2 y
10
y
х 3 2
х 2 3
х 4
Ответ: АВ=4 см,
ВС=6 см
C





















 Математика
Математика








