Похожие презентации:
Простейший многоугольник - треугольник
1. Треугольник и все что его касается.
2. Треугольник
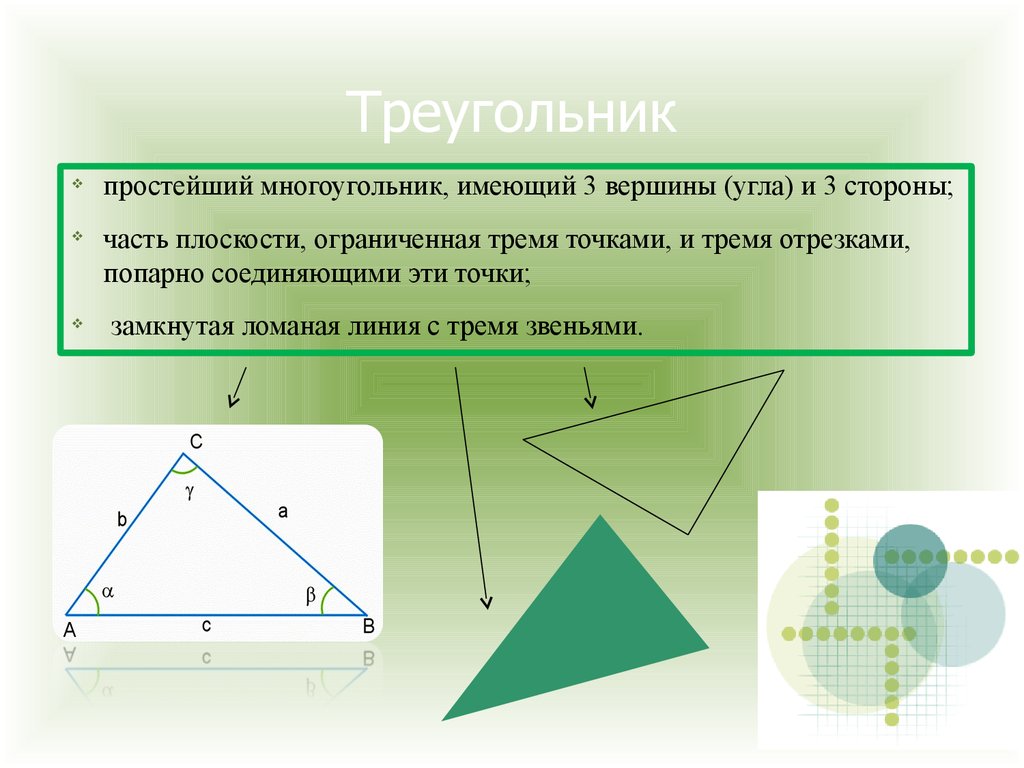
простейший многоугольник, имеющий 3 вершины (угла) и 3 стороны;часть плоскости, ограниченная тремя точками, и тремя отрезками,
попарно соединяющими эти точки;
замкнутая ломаная линия с тремя звеньями.
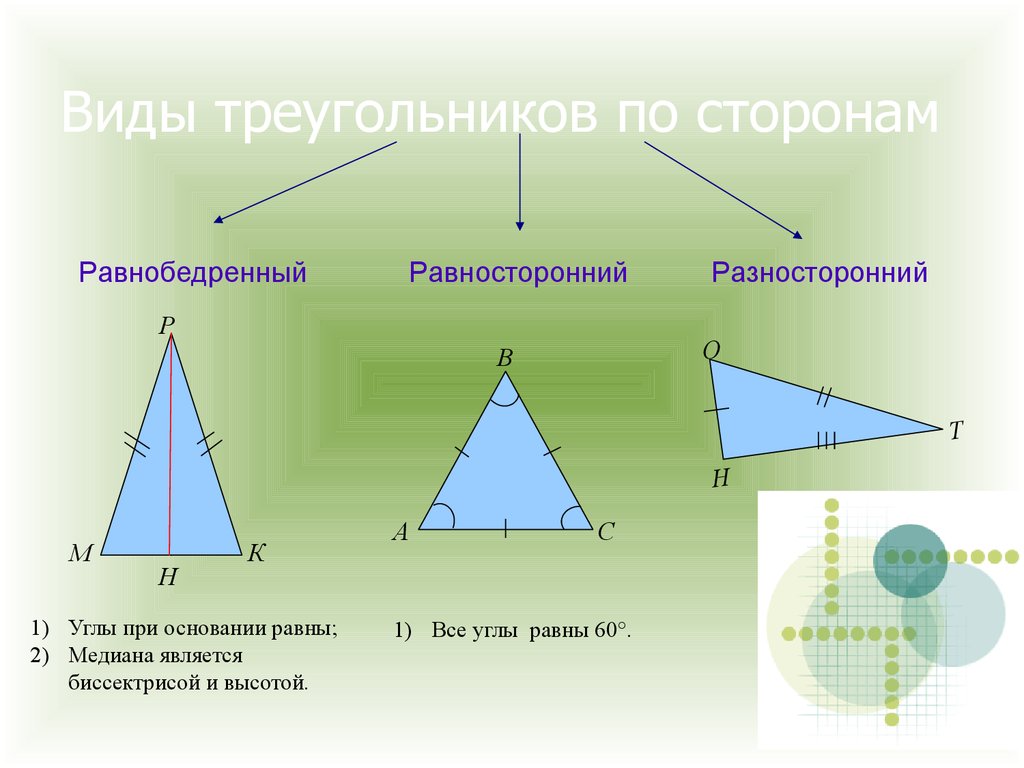
3. Виды треугольников по сторонам
РавнобедренныйРавносторонний
Р
Разносторонний
О
В
Т
Н
М
H
К
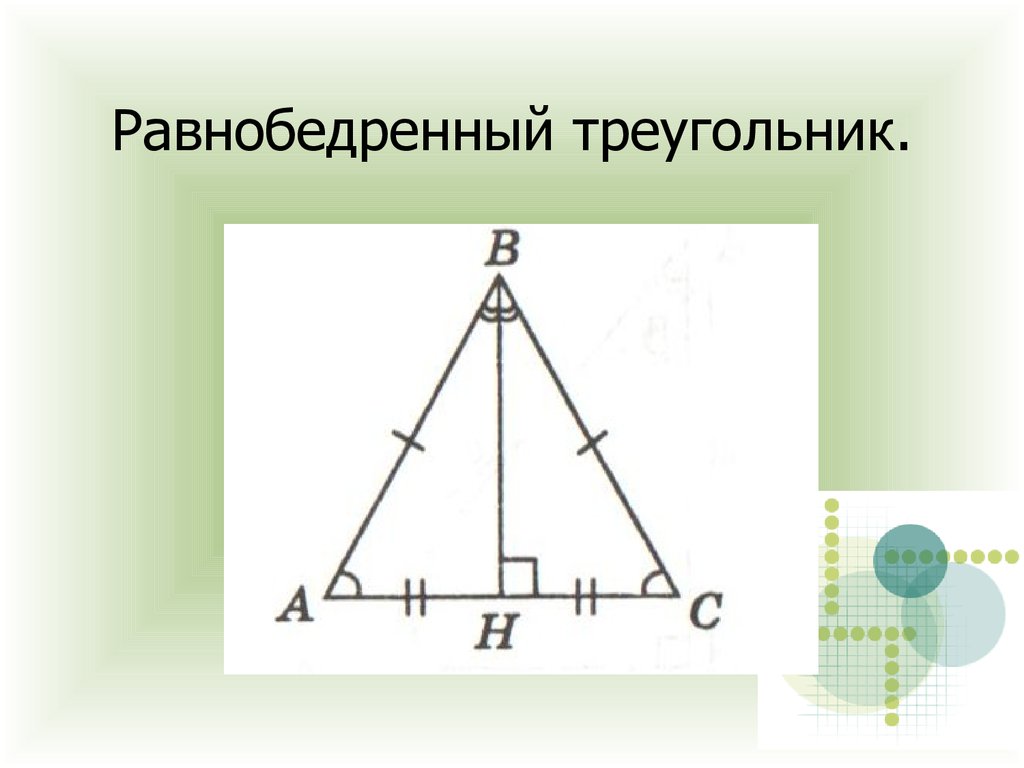
1) Углы при основании равны;
2) Медиана является
биссектрисой и высотой.
А
С
1) Все углы равны 60°.
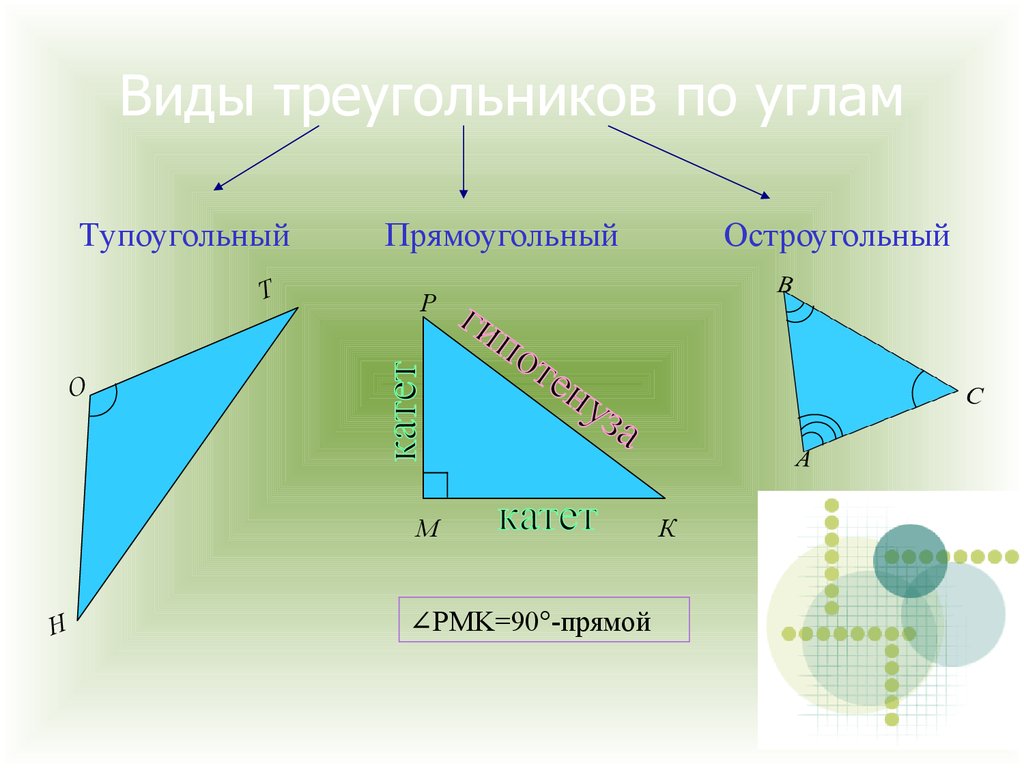
4. Виды треугольников по углам
ТупоугольныйТ
Прямоугольный
Остроугольный
Р
О
М
Н
∠PMK=90°-прямой
К
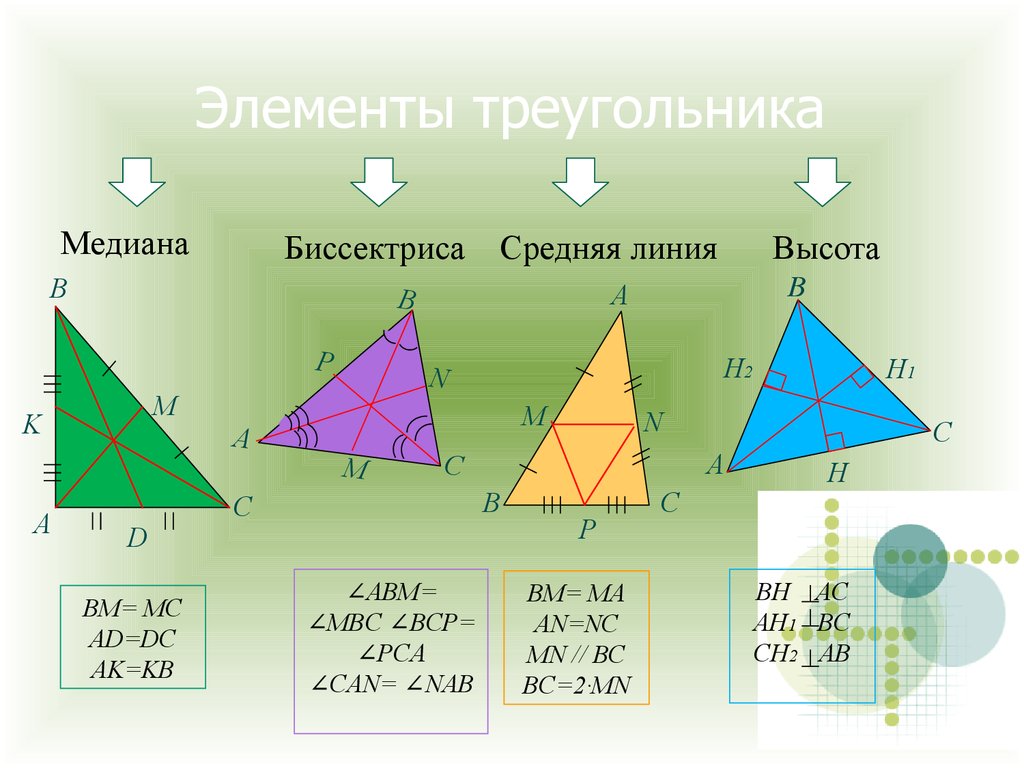
5. Элементы треугольника
МедианаБиссектриса
B
M
K
D
BM= MC
AD=DC
AK=KB
A
B
H2
N
M
M
Высота
A
B
P
A
Средняя линия
N
C
∠ABM=
∠MBC ∠BCP=
∠PCA
∠CAN= ∠NAB
C
A
B
C
H1
P
BM= MA
AN=NC
MN // BC
BC=2·MN
C
H
BH AC
AH1 BC
CH2 AB
6.
Свойства медиан треугольника:1. Медианы треугольника делятся
точкой пересечения в отношении
2:1(считая от вершины треугольника).
2. Медиана делит треугольник, равных
по площади на два треугольника.
7. Высота треугольника.
8. Биссектриса треугольника.
Свойства биссектристреугольника:
1. Биссектриса делит
противолежащую сторону на
части, пропорциональные
прилежащим сторонам.
2.Биссектриса треугольника делит
площадь треугольника в
отношении, пропорциональном
прилежащим сторонам.
3. Точка пересечения биссектрис
треугольника является центром
окружности, вписанной в этот
треугольник.
9.
Средняя линияСредней линией треугольника называется
отрезок, соединяющий середины двух его
сторон.
Свойство средней линии треугольника
Средняя линия треугольника параллельна одной
из его сторон и равна половине этой стороны.
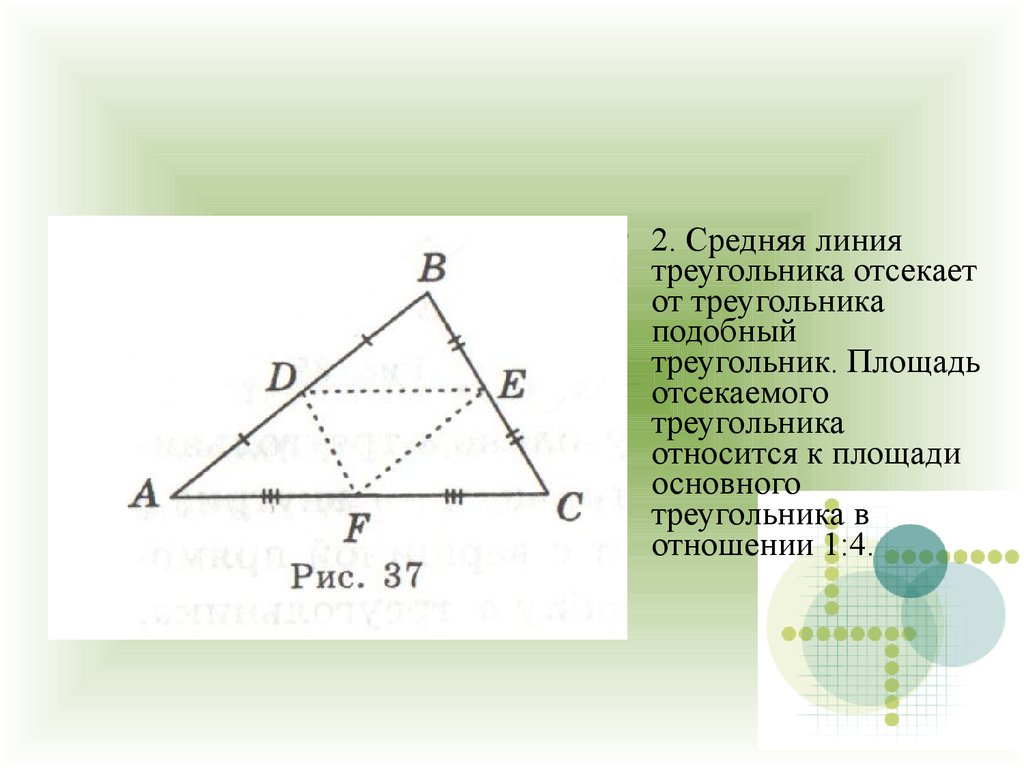
10.
2. Средняя линиятреугольника отсекает
от треугольника
подобный
треугольник. Площадь
отсекаемого
треугольника
относится к площади
основного
треугольника в
отношении 1:4.
11.
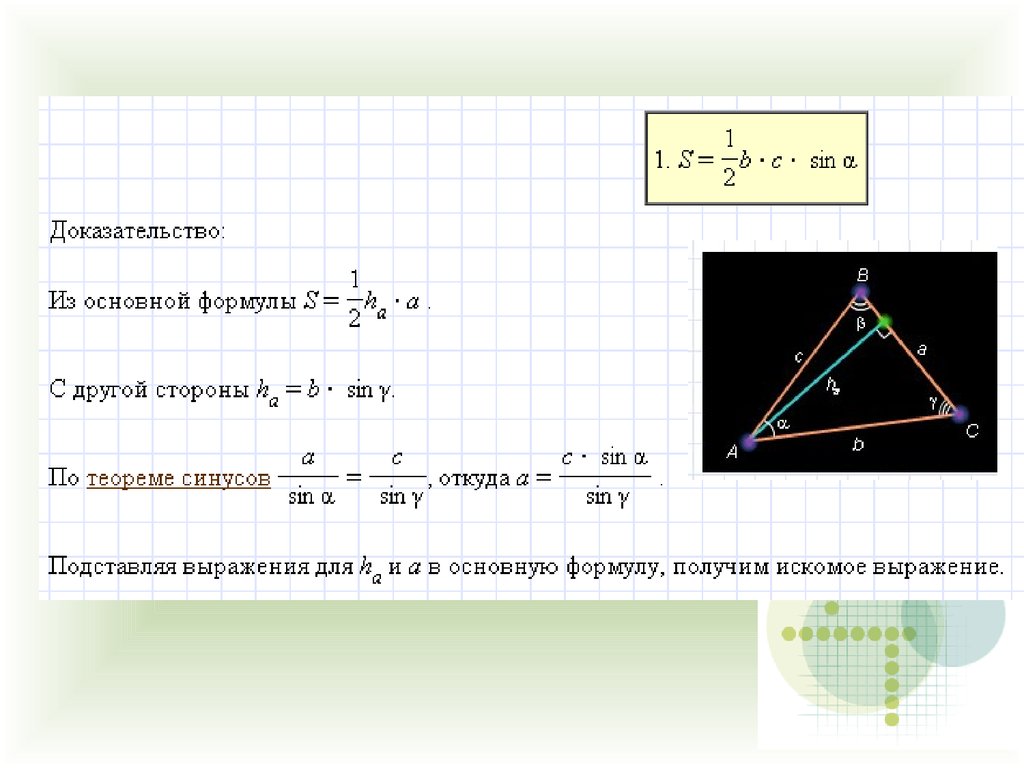
12. Площадь треугольника.
13.
14.
15.
16. Площадь треугольника
S ( п/у)=
1
· a · b.
2
b
a
h1= h2 =>
S1
S2
=
AC
A1C1
.
S1
h1
A
∠1= ∠2=>
S1
S2
S2
h1
C A1
AC·AB
= A1C1·A1B1
C1
B1
B
1
A
S1
2
C
A1
S2
C1
17. Равенство треугольников
Признаки равенства треугольников:1. По двум сторонам и углу между ними.
2. По стороне и двум прилежащим к ней углам.
3. По трём сторонам.
18. Подобие треугольников
Признаки подобия треугольников:1. По двум углам.
2. По двум сторонам и углу между ними.
3. По трём сторонам.
19. Равнобедренный треугольник.
20. Равносторонний треугольник.
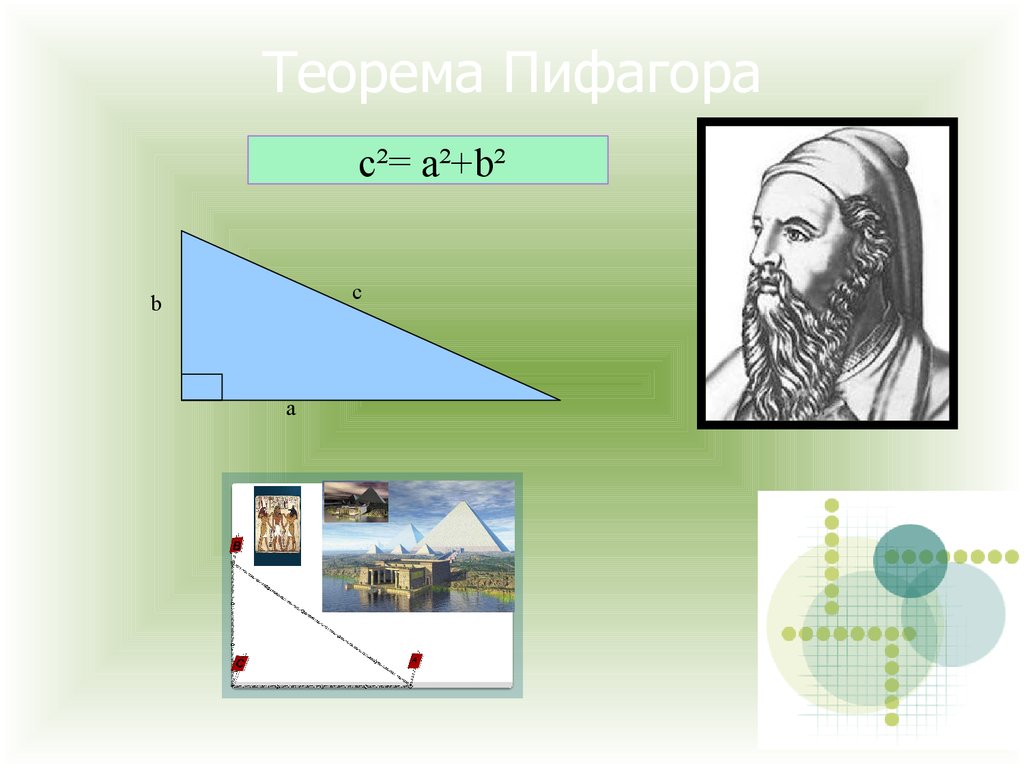
21. Теорема Пифагора
c²= а²+b²c
b
a
22. Доказательство теоремы Пифагора
Дано: а,b- катеты, с-гипотенуза.Доказать: a2+b2=c2.
Доказательство:
Достроим до квадрата со стороной (a+b).
S1=(a+b)2
S2=4(1/2ab)+c2
Приравняем площади:S1=S2.
(a+b)2=4(1/2ab)+c2
а2+2ab+b2=2ab+c2
а2+b2=c2
23. Задача
Вот задача индийского математика 12в. БхаскарыНа берегу реки рос тополь одинокий. Вдруг ветра порыв его
ствол надломал. Бедный тополь упал. И угол прямой с
теченьем реки его ствол составлял. Запомни теперь, что в
том месте река в четыре лишь фута была широка. Верхушка
склонилась у края реки. Осталось три фута всего от ствола,
прошу тебя, скоро теперь мне скажи: у тополя как велика
высота?
Решение:
По теореме Пифагора находим СD:
CD2 = 3 2 + 4 2 = 9 + 16 =25 => CD= 5.
Высота тополя равна: CB+CA. Т.к.
CD=CB =>
AB=AC+CD= 3 + 5 = 8.
Ответ: высота тополя 8 футов.
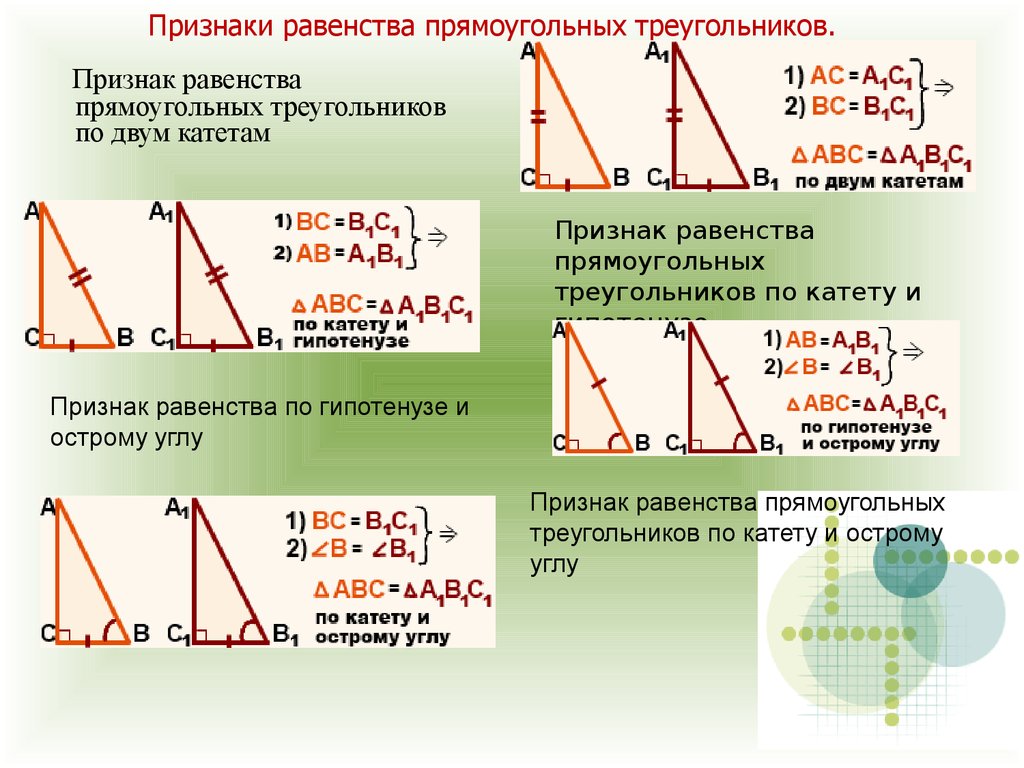
24. Признаки равенства прямоугольных треугольников.
Признак равенствапрямоугольных треугольников
по двум катетам
Признак равенства
прямоугольных
треугольников по катету и
гипотенузе
Признак равенства по гипотенузе и
острому углу
Признак равенства прямоугольных
треугольников по катету и острому
углу
25. Свойства прямоугольного треугольника
1. Сумма острых углов прямоугольного треугольника равна 90˚.2. Катет, противолежащий углу в 30˚, равен половине гипотенузы.
3. И обратно, если в треугольнике катет вдвое меньше гипотенузы, то напротив него
лежит угол в 30˚
.
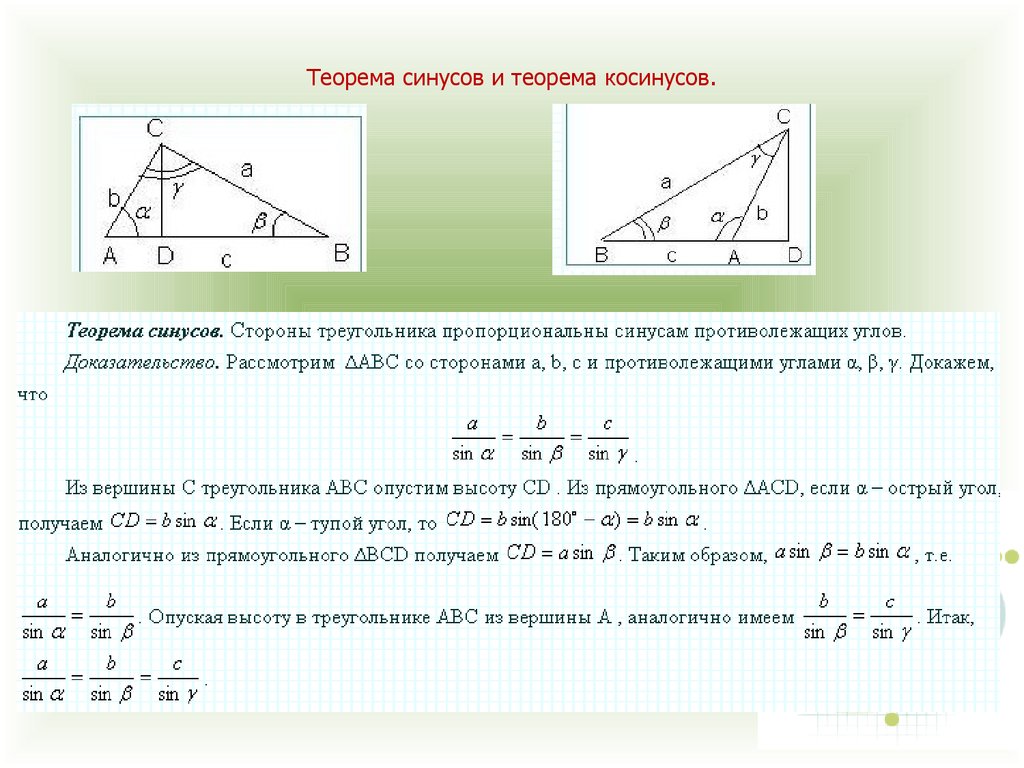
26. Теорема синусов и теорема косинусов.
27. Теорема косинусов.
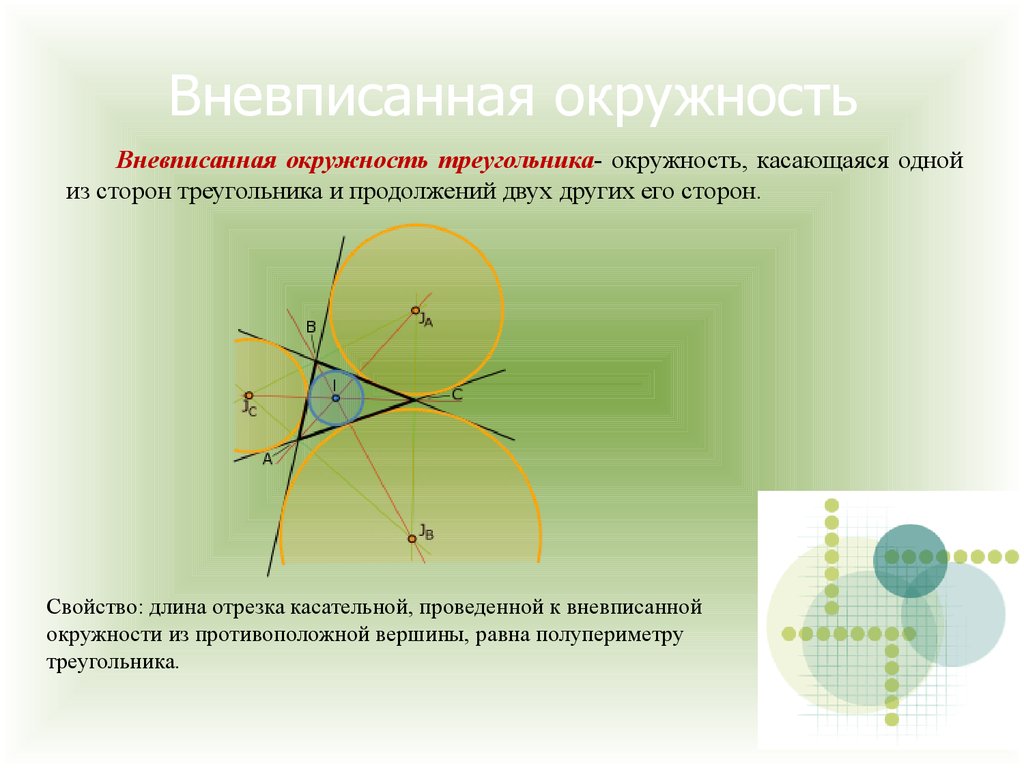
28. Вневписанная окружность
Вневписанная окружность треугольника- окружность, касающаяся однойиз сторон треугольника и продолжений двух других его сторон.
Свойство: длина отрезка касательной, проведенной к вневписанной
окружности из противоположной вершины, равна полупериметру
треугольника.
29.
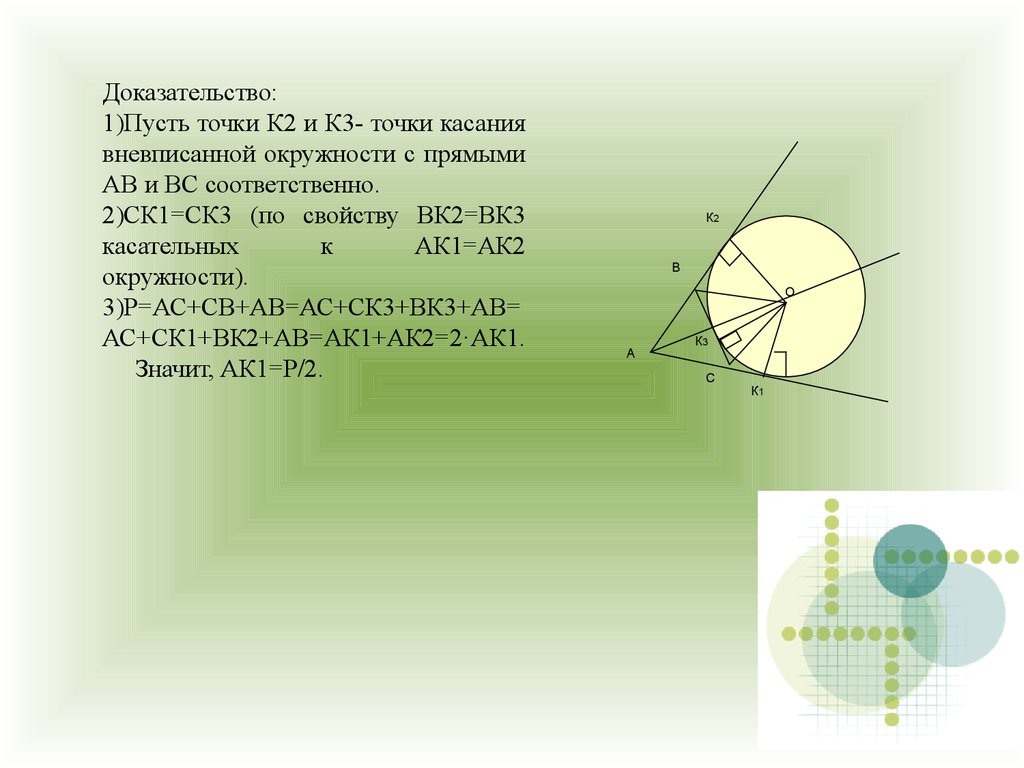
Доказательство:1)Пусть точки К2 и К3- точки касания
вневписанной окружности с прямыми
АВ и ВС соответственно.
2)СК1=СК3 (по свойству ВК2=ВК3
касательных
к
АК1=АК2
окружности).
3)Р=АС+СВ+АВ=АС+СК3+ВК3+АВ=
АС+СК1+ВК2+АВ=АК1+АК2=2·АК1.
Значит, АК1=Р/2.
К2
В
О
А
К3
С
К1
30. Расстояние от инцентра треугольника до его вершин
Теорема1:
Биссектриса
противоположную
сторону
на
соответствующим боковым сторонам.
угла
треугольника
делит
отрезки,
пропорциональные
А
c
b
С
L a
В
Следствие: Пусть AL-биссектриса ∠А в ΔАВС. Тогда отрезки CL и LB
находятся по формулам:
,
.
31.
Дано: ВК- биссектриса, СМ||ВКДоказательство: Так как ВК – биссектриса АВС, то АВК= КВС. Далее,
АВК= ВМС, как соответственные углы при параллельных прямых, и КВС= ВСМ,
как накрест лежащие углы при параллельных прямых. Отсюда ВСМ= ВМС, и
поэтому треугольник ВМС – равнобедренный, откуда ВС=ВМ. По теореме о
параллельных прямых, пересекающих стороны угла, имеем АК/КС=АВ/ВМ=АВ/ВС,
что и требовалось доказать.
32.
Теорема 2: Пусть в ΔАВС из вершины ∠А проведена биссектриса l, которая делитсторону СВ на отрезки CL=m, LB=n. Тогда справедливо равенство:
А
b
С
c
l
m
n
В
L1
d
P
Теорема 3: Для всякого ΔАВС справедливы равенства:
33.
Инцентр- точка пересечения биссектрис треугольника.A
I
C
L
B
Расстояние от инцентра треугольника до его вершин вычисляется по формулам:
34. Свойства медиан
Теорема: Если a, b, с- стороны ΔАВС (рис.34), ma, mb, mc- его медианы, проведенные к соответствующим сторонам, то справедливы формулы:B
D
ma
A
A1
C
35.
BD
ma
A
A1
C
36.
37.
ЗадачаB
b
b
C
a
a
A
38. Спасибо за внимание!
39. Теорема синусов и косинусов
Теорема синусов:a
b
c
=
=
= 2·R.
sin a
sin b sin c
c
a
b
a
c
Теорема косинусов:
a2 = b2 + c 2 -2·b·c·cos a.
b
R



























 Математика
Математика