Строительная механика стержней. Устойчивость стержней

1. СТРОИТЕЛЬНАЯ МЕХАНИКА

Строительная механика стержней
Устойчивость стержней
Доцент кафедры
«Самолетостроение»
к.т.н. Мухин Д.В.

2.

1. Основные понятия теории устойчивости
Потеря устойчивости, связанная с отклонением упругой системы от
первоначального положения равновесия является одной из наиболее
распространенных форм разрушения стержневых и тонкостенных элементов
летательных аппаратов. Понятие устойчивости связано с характером реакции
нагруженной системы на воздействие некоторых дополнительных
возмущений – если после исчезновения этого возмущения система под
действием упругих сил возвращается в исходное состояние, то это состояние
считается устойчивым. Естественно, что реакция системы зависит от уровня
ее нагружения, характера и величины возмущения. В дальнейшем будем
считать, что возмущение по своему характеру способствует переходу
системы в новое состояние, а по величине является малым. Таким образом,
требуется определить уровень нагружения системы, при котором малое
возмущение может привести к изменению ее состояния, т. е. к потере
устойчивости. Минимальная нагрузка, при которой возникает такая ситуация,
называется критической. Ввиду того, что элементы летательных аппаратов
эксплуатируются при высоких уровнях нагружения и в условиях постоянного
воздействия возмущающих факторов самой различной природы, конструктор
должен предвидеть возможность потери устойчивости и иметь информацию о
критических уровнях нагрузок, определению которых посвящена настоящая
лекция.

3.

1.1 Статический критерий устойчивости
Основные подходы к исследованию устойчивости
упругих систем можно проанализировать на простых
примерах. Рассмотрим сначала сжатие вертикального
жесткого стержня с упругим шарниром.
Положение такого стержня как системы с одной
степенью свободы вполне определяется углом φ,
отсчитываемым от вертикали. Отклоним стержень от
исходного вертикального положения на некоторый угол
φ и исследуем его равновесие. Сила Р создает
опрокидывающий момент P·l·sin φ, а пружина с
жесткостью с — восстанавливающий момент т =с·φ,
т.е условие равновесия имеет вид
P l sin c
Это уравнение при любом Р имеет тривиальное (нулевое) решение φ=0, т. е.
вертикальная форма равновесия в принципе возможна при любом Р. Для
дальнейшего анализа представим sin φ степенным рядом
sin
3
3!
5
5!
...

4.

Тогда уравнение равновесия примет вид
1
2
3!
4
5!
...
P1
P
где P1 c l
.
Поскольку левая часть уравнения меньше 1, его решение существует только
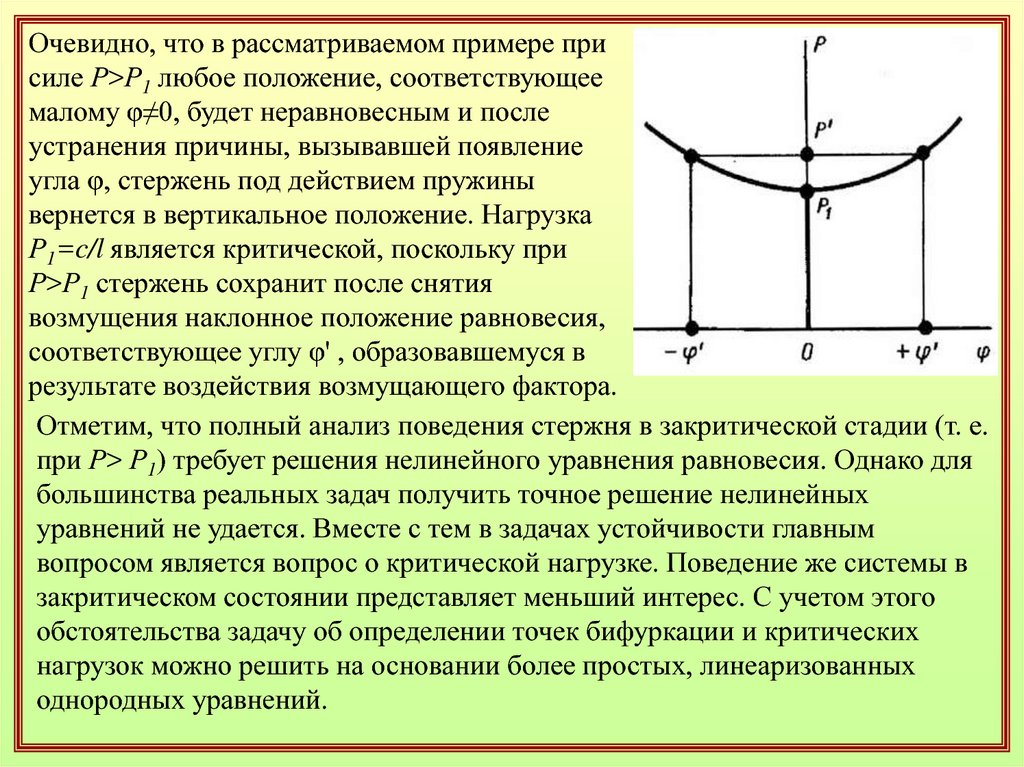
при Р≥ Р1. Это решение показано на рисунке.
Таким образом, при Р<Р1 существует только
начальное (вертикальное) положение
равновесия, а при Р'>Р1 возможны три
положения равновесия, соответствующие φ=0,
φ=φ', φ=-φ'.
Точка, при переходе через которую возможна
неоднозначность положения равновесия,
называется точкой бифуркации или точкой
ветвления решения.
В рассматриваемом примере такой точкой является точка, соответствующая
силе Р1=с/l. Равновесное состояние упругой системы считается устойчивым,
если, получив малое возмущение (малое отклонение), система возвращается
к исходному положению после снятия возмущения. Нагрузка, при которой
начальная форма (или положение) перестает быть устойчивой, называется
критической, а соответствующее состояние — критическим.

5.

Очевидно, что в рассматриваемом примере при
силе Р>Р1 любое положение, соответствующее
малому φ≠0, будет неравновесным и после
устранения причины, вызывавшей появление
угла φ, стержень под действием пружины
вернется в вертикальное положение. Нагрузка
Р1=c/l является критической, поскольку при
Р>Р1 стержень сохранит после снятия
возмущения наклонное положение равновесия,
соответствующее углу φ' , образовавшемуся в
результате воздействия возмущающего фактора.
Отметим, что полный анализ поведения стержня в закритической стадии (т. е.
при Р> Р1) требует решения нелинейного уравнения равновесия. Однако для
большинства реальных задач получить точное решение нелинейных
уравнений не удается. Вместе с тем в задачах устойчивости главным
вопросом является вопрос о критической нагрузке. Поведение же системы в
закритическом состоянии представляет меньший интерес. С учетом этого
обстоятельства задачу об определении точек бифуркации и критических
нагрузок можно решить на основании более простых, линеаризованных
однородных уравнений.

6.

Такие уравнения строятся при рассмотрении равновесия системы в
положении, близком к исходному положению. При этом важно подчеркнуть,
что в задачах устойчивости уравнения равновесия составляются для
деформированной системы. Линеаризованные уравнения позволяют
определить условия, при которых наряду с исходным равновесным
состоянием могут быть и другие, близкие к исходному, равновесные
состояния. Например, для приведенного выше примера такое уравнение
можно получить, если принять, что стержень отклонен от вертикали на
малый угол φ, для которого можно принять, что sinφ≈φ. В результате такой
линеаризации уравнение равновесия принимает вид Ρ·l·φ=с·φ и имеет два
решения – φ=0 при любом Р и Р=Р1=с/l при ·φ≠0. Таким образом,
линеаризованное уравнение позволяет определить критическую нагрузку и
не позволяет в отличие от нелинейного уравнения найти φ, т. е. определить
перемещение, образующееся в результате потери устойчивости.
В заключение сформулируем статический критерий устойчивости Л. Эйлера.
Согласно этому критерию критическим называется наименьшее значение
нагрузки, при котором кроме исходного положения равновесия система
может иметь по крайней мере еще одно, близкое к исходному положение
равновесия.

7.

Отметим, что для задач устойчивости характерно наличие двух или более
равновесных состояний, соответствующих одной и той же нагрузке, т. е.
бифуркация форм равновесия. В статическом критерии не содержится
указания на то, какая из возможных форм равновесия является устойчивой,
однако применительно к упругим системам достижение нагрузкой
критического значения, как правило, означает, что исходная форма
равновесия становится неустойчивой.
Реализация статического критерия устойчивости, т. е. определение
критической нагрузки осуществляется по следующей схеме:
1. Рассматривается докритнческое (исходное) состояние системы и по
заданным внешним нагрузкам определяются докритические
напряжения. Ввиду того, что докритические перемещения, как правило,
невелики, они не учитываются и далее исследуется исходная система, на
которую уже не действует внешняя нагрузка, но в которой существует
найденное докритическое напряженное состояние.
2. Этой системе придаются некоторые дополнительные малые
перемещения (возмущения), соответствующие возможной форме потери
устойчивости, и записываются уравнения равновесия для возмущенного
состояния.

8.

Эти уравнения являются, линейными и однородными относительно
дополнительных перемещений и всегда включают две группы членов —
члены, соответствующие упругим силам, стремящимся ликвидировать
возмущения, и параметрические члены, включающие докритические
напряжения и соответствующие силам, стремящимся вывести систему из
исходного состояния.
3. Необходимо найти такую комбинацию докритических напряжений, при
которой уравнения равновесия имели бы нетривиальное решение,
удовлетворяющее заданным граничным условиям, т. е. существовали бы
равновесные дополнительные перемещения, соответствующие условиям
закрепления системы. Как правило, такая комбинация оказывается не
единственной и выбирается та, которая соответствует минимальному
значению внешней нагрузки. Это значение и является критическим.
Формально отыскание критической нагрузки соответствует определению
минимального собственного значения краевой задачи для уравнений
равновесия, записанных в возмущенном состоянии. Отметим, что операция
наложения возмущения является чисто формальной и связана с тем, что в
теории устойчивости рассматриваются идеальные системы и идеальные
условия нагружения. В реальных системах возмущения, вызывающие малые
отклонения, всегда присутствуют — это дополнительные случайные нагрузки,
несовершенства формы и т. д.

9.

1.2 Энергетический критерий устойчивости
Определить критическое состояние и соответствующую нагрузку можно и на
основании анализа энергетических зависимостей упругой системы при
переходе ее из одного состояния в другое. При этом, как и в случае
статического критерия устойчивости, нужно рассмотреть некоторое
начальное (докритическое) состояние равновесия и близкое к нему
возмущенное состояние. Согласно вариационному принципу Лагранжа в
состоянии равновесия вариация полной энергии должна обращаться в нуль, т.
е.
Э 0
Строго говоря, это равенство обеспечивает стационарность полной энергии,
т. е. при δЭ=0 энергия Э может быть минимальной или максимальной.
Согласно теореме Лагранжа—Дирихле равновесное положение,
определяемое условием равновесия, является устойчивым, если реализуется
минимум полной энергии (т. е. δ2Э>0), и неустойчивой, если реализуется
максимум (т. е. δ2Э<0). Критическому состоянию, очевидно, соответствует
условие
2
Э 0
Таким образом, согласно энергетическому критерию устойчивости критическая величина нагрузки обращает в нуль вторую вариацию полной
энергии.

10.

Рассмотрим с позиций этого критерия систему,
показанную
на рисунке. Создадим малое отклонение φ.
,
Тогда согласно определению полной энергии Э=U-А.
Потенциальная
энергия U накапливается в пружине, т. е.
,
U
1
1
m c 2,
2
2
а работа А совершается силой Р на перемещении
Δ=l·(1-cosφ) . Считая φ малым, учтем, что cosφ≈1-φ2/2,
т. е.
P
2
A
Таким образом
l
2
l c
Э P 2
2 l
c
l
Э l P
c
l
2 Э l P 2
Отсюда при 2 Э 0 получим P≈P1=c/l, т. е. результат, найденный ранее с
помощью статического критерия. Очевидно, при P P1 2Э 0 и исходное
вертикальное положение стержня является устойчивым, а при P P1 2Э 0
и это положение становится неустойчивым.

11.

Приведем еще одно энергетическое соотношение, которое часто
используется для определения критической нагрузки. При переходе из
начального (равновесного) состояния в смежное (не обязательно
равновесное) упругая система приобретает дополнительную потенциальную
энергию деформации U, которая способствует возврату системы в исходное
положение, а внешние силы, способствующие развитию отклонения,
совершают при этом работу А. Если эта работа меньше соответствующей
энергии деформации, то начальное состояние упругой системы является
устойчивым, а если больше — неустойчивым. Очевидно, критическому
состоянию соответствует условие U=A.
В частности, для рассмотренного выше стержня из равенств
U
1
c 2 ,
2
A
P
l 2
2
получим P=P1=c/l т. е. прежнее выражение для критической нагрузки.

12.

2 ПРИКЛАДНЫЕ МЕТОДЫ РАСЧЕТА НА УСТОЙЧИВОСТЬ
2.1 Метод Эйлера
Рассмотрим стержень, сжатый осевой силой
Р (рис. 9.3). Очевидно, в докритическом,
прямолинейном состоянии в стержне будет
только продольное усилие Р.
В соответствии со статическим критерием устойчивости придадим стержню
малый прогиб v(х) и исследуем равновесие искривленной формы. Для
вывода уравнения устойчивости применим метод, который будет
неоднократно использоваться далее. Запишем уравнение изогнутой оси
стержня, нагруженного некоторым поперечным давлением q.
Как было показано ранее уравнение
равновесия при таком нагружении имеет вид
EJ v IV x q x

13.

На рассматриваемый стержень, поперечная нагрузка не действует, однако в
изогнутом состоянии воздействие усилия Р можно заменить воздействием
статически эквивалентной условной поперечной нагрузки q .
Действительно, приравнивая вертикальные равнодействующие сил,
показанных на рисунках, получим Р·sinα1-Р·sinα2=qdx.
Учитывая, что для малых прогибов v(x) sinα≈tgα≈α и 1 v
2 v
dv
dx v v dx
dx
будем иметь – P v q
. Этот результат можно записать в несколько
иной форме, если учесть формулу для кривизны оси стержня и ее
упрощение для малых прогибов (v'<<1)
v
1 v
2
3
v
2

14.

Таким образом, для стержня
q P P v
Уравнение устойчивости теперь может быть записано, если в уравнении
равновесия стержня, нагруженного распределенной нагрузкой,
рассмотренном ранее, заменить q на q согласно полученной зависимости.
В результате получим EJ v IV P v 0
Это линейное ОДУ. Общее решение данного уравнения имеет вид
v C1 C2 x C3 sin kx C4 cos kx
где k P EJ
Для шарнирно опертого стержня имеем следующие граничные условия
(смещение Δ является малым и не учитывается): при x=0 и x=l v=v''=0.
Подставляя ГУ в общее решение имеем
С1 С4 0,
С1 С2 l C3 sin kl C4 cos kl 0,
C4 0,
C3 sin kl C4 cos kl 0.
Отсюда C1=C2=C4=0, C3·sin kl=0. Если принять С3=0, то получим v=0, т. е.
исходную прямолинейную форму. Таким образом, для существования
изогнутой формы равновесия необходимо выполнение равенства sin kl=0,
возможное, если kl=n·π (n=1,2,3…). Учитывая, что k P EJ получим
Pn n 2 EJ l 2 — совокупность значений силы Р, при которых возможна
изогнутая форма равновесия.

15.

Согласно определению критической нагрузки из этих значений следует
выбрать наименьшее, которое соответствует, очевидно, n=1. Таким образом,
получили формулу Эйлера, определяющую критическую нагрузку для
сжатого шарнирно опертого стержня
2 EJ
Pкр
l2
При P=Pкр имеем k=π/l и, поскольку в общем решении ДУ отлична
от нуля только постоянная С3, получаем функцию прогиба
v C3 sin
x
l
т. е. стержень изгибается при потере устойчивости по одной полуволне
(п=1) синусоиды . Амплитуда прогиба С3, как уже отмечалось, из решения
линеаризованного уравнения (9.12) не определяется. Для того чтобы найти
прогиб, необходимо рассмотреть полное нелинейное уравнение, которое для
исследуемого стержня записывается достаточно просто. Действительно,
изгибающий момент, образующийся в сечении стержня при изгибе, связан с
кривизной следующим образом M EJ , а внешний изгибающий момент
равен Ρ·ν . Таким образом, EJ P v , где κ определяется равенством
v
1 v
2
3
2

16.

Выше был рассмотрен метод определения критической нагрузки,
основанный на непосредственном интегрировании уравнения устойчивости
и удовлетворении граничных условий. В случае шарнирного опирания
точное решение может быть построено также в форме ряда, каждый член
которого заведомо удовлетворяет граничным условиям.
Для стержня, показанного на рисунке
такой ряд имеет вид
m x
m 1
l
v sin
Очевидно, каждый член ряда автоматически удовлетворяет граничным
условиям шарнирного опирания v(0)=v(l)=v''(0)=v''(0)=0.

17.

В качестве примера рассмотрим задачу
об устойчивости сжатого стержня,
лежащего на упругом основании.
Такая расчетная схема может быть использована для анализа общей
устойчивости пояса лонжерона, лежащего на упругих опорах.
Уравнение устойчивости для данного случая может быть получено из
уравнения равновесия стержня, нагруженного распределенной нагрузкой, в
котором следует принять q=-P·v''-c·v. Второе слагаемое определяет реакцию
упругого основания, пропорциональную прогибу ν и коэффициенту
упругого основания с. Подставляя получим
EJ v IV c v P v 0
m x
Подставляя ряд v sin
, будем иметь
l
m 1
A EJ
m 1
m
4
m
c P 2m sin m x 0 где m m l
Выполнение этого равенства возможно только в случае, когда выражение в
скобках равно нулю (случай Ат=0 исключается, так как при этом v=0), т. е.
P EJ 2m c m2

18.

Важно. В данном случае минимальное значение критической силы не будет
соответствовать минимальному количеству полуволн.
Для определения критической силы в полученной формуле следует
последовательно принять т = 1, 2, 3 ... и из полученных значений Р выбрать
наименьшее. Для длинного стержня, где количество полуволн может быть
большим, параметр λm можно приближенно считать непрерывным и
осуществить минимизацию Рп аналитически. Из условия dP d m 0
получим 4m c EJ , т. е. Pкр 2 c EJ .

19.

2.2 Метод Ритца—Тимошенко
Метод Ритца—Тимошенко в задачах
устойчивости является вариантом общего
метода, рассмотренного ранее. Рассмотрим
использование этого метода на задаче об
устойчивости стержня.
Получим выражение для полной энергии. Потенциальная энергия изогнутого
стержня неоднократно записывалась ранее и имеет вид
l
U
0
EJ
v 2 dx
2
Работа внешней силы согласно рисунка равна Р·Δ. Найдем величину Δ.
Длину элемента дуги искривленного стержня с учетом малости прогиба
(v'<<1) можно записать следующим образом:
1 2
2
ds 1 v dx 1 v dx
2
Тогда полная длина искривленной оси, равная исходной длине прямого
стержня, будет
l
0
1 2
1 2 v dx l

20.

Рассчитываем первый интеграл суммы и выражаем перемещение Δ
l
l
1
1
2
2
v dx v dx
2 0
20
l
Таким образом
P
2
A v dx
20
l
и полная энергия искривленного стержня
1
2
2
Э EJ v P v dx
20
В соответствии с общим методом Ритца—Тимошенко представим прогиб в
n
виде ряда
v( x) Bi vi x
i 1
где Bi – неизвестные независимые коэффициенты; vi(х) — задаваемые
непрерывные функции, удовлетворяющие, по крайней мере, геометрическим
граничным условиям. Если выражение для функции прогиба подставить в
формулу для полной энергии, то получим
2
2
l
n
n
1
Э EJ Bi vi P Bi vi dx
2 0
i 1
i 1
т. е. при известных функциях vi(х) энергия становится квадратичной формой
коэффициентов Вi.

21.

В соответствии с общим методом, далее следует записать условия минимума
полной энергии Э
Э
0 i 1,2,3,..., n
Bi
которые образуют систему линейных однородных уравнений в матричном
виде имеющих вид:
a B P b B 0
где В – матрица-столбец порядка п искомых коэффициентов Βi; а и b —
квадратные матрицы порядка п, элементы которых вычисляются по формулам
l
aij EJ vi v j dx,
0
l
bij vi v j dx i, j 1,2,3,..., n
0
Ввиду того, что однородная система должна иметь нетривиальное решение
(случай Вi=0 соответствует исходной прямолинейной форме равновесия
стержня), ее определитель должен быть равен нулю, т. е.
det aij P bij 0
Полученное характеристическое уравнение позволяет найти критическую
силу.

22.

В качестве примера рассмотрим стержень,
показанный на рис. 9.3, и зададим его прогиб
в виде комбинации следующих функций,
удовлетворяющих геометрическим
граничным условиям ν(0)=ν(l)=0:
v2 x x 2 l x 2
где v1 x x l x
v B1 v1 x B2 v2 x
Полная энергия после вычисления интегралов принимает вид
Э
1
EJ 4 B12 l 0,8 B22 l 5 P 0,333 B12 l 3 6,133 B1 B2 l 5 0,019 B22 l 7
2
Система уравнений, выражающих условие минимума полной энергии после
вычисления производных примет вид
8 0,666 P B 6,133 P B l
6,133 P B 1,6 0,038 P B
2
1
2
1
2
0,
l 0.
2
где P P l 2 EJ
Так как l – длина стержня в данной задаче есть величина постоянная
проведем замену переменной B*=B2·l2. Получим
8 0,666 P B 6,133 P B 0,
6,133 P B 1,6 0,038 P B 0.
*
1
*
1

23.

Приравнивая нулю определитель данной системы, получим следующее
характеристическое уравнение
2
P 54,1 P 1137 0
EJ
Минимальный корень этого уравнения равен P кр 11,8 , т.е. Pкр 11,8 2
l
что превышает точное значение на 19,7%.
В случае одночленной аппроксимации прогиба v=В1·v1(х) для получения
критической силы удобнее использовать энергетическое соотношение U=А.
С учетом равенств полученный выше выражений для U и А
l
l
P
2
A v dx
20
EJ
v 2 dx
U
2
0
получим формулу Релея-Ритца
l
Pкр
2
EJ
v
1 dx
0
l
2
v
1 dx
0
Полагая, например, для шарнирно опертого стержня v1 x x l x получим
Pкр 12EJ / l 2

24.

Отметим, что задание прогиба v(x) в форме ряда по существу соответствует
введению некоторых дополнительных связей, вынуждающих систему
деформироваться в соответствии с заданным законом. Эти связи,
естественно, повышают жесткость системы, а поскольку при увеличении
жесткости увеличивается и критическая нагрузка, результат, полученный
методом Ритца— Тимошенко, всегда будет верхней оценкой критической
нагрузки. Он будет тем ближе к истинному значению, чем лучше
представление v(x) соответствует истинной форме потери устойчивости.
Если в качестве аппроксимирующей функции принята действительная
форма потери устойчивости, результат оказывается точным. Действительно,
зададим для шарнирно опертого стержня в соответствии с точным решением
v1(x)=sin(πх/l). Тогда по формуле Релея-Ритца получим
Pкр
EJ
4 l
2
l 4 2 EJ
2 l
l2
l2 2
что совпадает с точным результатом.

25.

2.3. Метод Бубнова—Галеркина
В задачах устойчивости упругой системы
применение метода Бубнова—Галеркина,
связано с приближенным определением
наименьшего собственного значения
уравнения устойчивости и соответствующей собственной функции.
Покажем принципиальную схему применения метода на примере сжатого
стержня, уравнение устойчивости которого имеет вид
L v EJ v IV P v 0
Прогиб стержня при потере устойчивости представим выражением,
аналогичным предыдущему методу
n
v( x) Bi vi x
i 1
где Βi – неизвестные коэффициенты, а vi(x)— аппроксимирующие функции,
которые согласно методу Бубнова—Галеркина должны удовлетворять всем
граничным условиям.

26.

Согласно общей схеме реализации метода, ряд, выражающий функцию
прогиба следует подставить в уравнение устойчивости и записать следующие
условия:
l
n
L
B
v
x
0 i 1 i i v j x dx 0
j 1,2,3,..., n
Эти уравнения составляют линейную однородную систему, которая может
быть записана в следующей матричной форме:
a P b 0
где а и b — квадратные матрицы порядка п, элементы которых вычисляются
по формулам
l
aij EJ v
IV
i
x v j x dx,
l
bij vi x v j x dx
0
0
Так же, как и в методе Ритца—Тимошенко, критическая нагрузка
определяется из характеристического уравнения, получаемого из условия
равенства нулю определителя системы.
det aij P bij 0

27.

Результат, найденный методом Бубнова—Галеркина, в силу причин,
изложенных в предыдущем методе, превышает истинное значение
критической нагрузки и совпадает с ним, если в разложении v(x) содержится
истинная форма потери устойчивости. Принимая, например, для шарнирно
4
3
опертого стержня v x B1 sin x l , получим a11 EJ 2 l ,
2
2
b11 2 2 l и Pкр a11 b11 EJ l т.е. точный результат.

28.

2.4. Метод конечных разностей
Метод конечных разностей основан на приближенной замене
дифференциальных уравнений системой алгебраических уравнений
относительно значений искомых функций в узловых точках.
Применение этого метода к задаче
устойчивости покажем на примере стержня,
уравнение устойчивости которого имеет
форму EJ v IV P v 0
Разделим стержень на п одинаковых участков длиной Δx=l/n и запишем
уравнение устойчивости в конечных разностях с помощью ранее
полученных формул конечных разностей.
В некоторой внутренней точке k получим
EJ
P
6
v
4
v
v
v
v
vk 1 vk 1 2 vk 0
k
k 1
k 1
k 2
k 2
x 4
x 2

29.

Записывая это уравнение при k=1,2,3,…,n и добавляя граничные условия,
которые формулируются с помощью законтурных точек, получим
однородную систему алгебраических уравнений относительно узловых
значений прогиба vk. Для существования ненулевого решения этой системы
необходимо, чтобы ее определитель равнялся нулю. Это условие и позволяет
найти критическую нагрузку.
Для стержня, показанного на рисунке, уравнения в точках 1, 2, 3 имеют вид
EJ
P
6
v
4
v
v
v
v
v A v2 2 v1 0,
1
A
2
a
3
4
2
x
x
EJ
P
6
v
4
v
v
v
v
v1 v3 2 v2 0,
2
1
3
A
B
4
2
x
x
EJ
P
6
v
4
v
v
v
v
v2 vB 2 v3 0,
3
2
B
1
b
4
2
x
x
Эти уравнения включают семь неизвестных – v1, v2, v3; прогибы в опорных
точках vA и vΒ и прогибы в двух законтурных точках vа и vb. Граничные
условия в точках A и В имеют вид v=v''=0. Через узловые значения они
формулируются с помощью уравнений конечных разностей следующим
образом:
vA 0, vB 0, va 2 vA v1 0, v3 2 vB vb 0

30.

Таким образом, к уравнениям необходимо добавить условия
vA 0, vB 0, va v1, vb v3
Учитывая, что в· силу симметрии прогиба v3 v1 и подставляя значение шага
x l 4 окончательно получим следующие два уравнения
24 2 P v P 16 v
32 2 P v 24 P v
1
2
0,
1
2
0
2
где P P l EJ
Приравнивая к нулю определитель этой системы, получим характеристическое уравнение
2
P 16 P 32 0
Наименьший корень этого уравнения соответствует величине Pкр 9,43 EJ l
которая на 4,3 % превышает точный результат. Так же, как методы Ритца—
Тимошенко и Бубнова-Галеркина, метод конечных разностей дает
завышенное значение для критической силы.
2