Устойчивость пластин

1. Устойчивость пластин

Доцент кафедры
самолетостроение
к.т.н. Мухин Д.В.

2.

1. Устойчивость прямоугольных пластин
1.1 Общие соотношения
Работая в условиях плоского
напряженного состояния и
воспринимая сжимающие
нормальные или касательные
усилия, пластины могут терять
устойчивость и принимать
искривленную форму типа
показанной на рисунке.
При решении задачи о потере устойчивости пластины кроме допущений, принятых
в теории изгиба пластин, предполагается, что до потери устойчивости пластина
является плоской, все силы лежат в срединной плоскости и при деформациях
пластины они не изменяются ни по величине, ни по направлению.
Итак будем считать, что докритическое напряженное состояние пластины является
плоским и описывается уравнениями, полученными ранее, т. е.
0
N y0 N xy0
u
0
0
0
N x0 N xy
v
Здесь N x , N y , N xy докрити
0;
0; N x0 B 0 0 ;
x
y
y
x
y
x
ческие усилия, которые
выражаются через докрити v
u v
u
B
N y0 B 0 0 ; N xy0 1 0 0 ;
0
0
0
ческие
напряжения
,
,
y
x
2
y
x
x
y
xy
формулами:
E h
B
N x0 x0 h N y0 y0 h N xy0 xy0 h
1 2

3.

Наиболее распространенным случаем
нагружения пластин, который и будет
рассматриваться далее, является воздействие
усилий, равномерно распределенных по
сторонам пластины. В этом случае уравнения
удовлетворяются тождественно, если поле
усилий является однородным, т. е
N x0 const
N y0 const
N xy0 const
Таким образом, докритические усилия, действующие в пластине, будем считать
0
0
0
известными и равными внешним усилиям N x , N y , N xy действующим по сторонам
пластины.
Придадим пластине малый прогиб w(х, у) и в соответствии со статическим
критерием устойчивости рассмотрим ее равновесие. Линеаризованное уравнение
устойчивости наиболее просто получить, если воспользоваться уравнением изгиба
пластины Софи Жермен.
D w q x, y
4
4w
4w
4w q
2 2 2 4
4
D
x
x y
y

4.

Заменим докритические усилия условной статически эквивалентной поперечной
нагрузкой q . Рассмотрим элемент пластины в изогнутом состоянии. Приравнивая
вертикальные проекции сил, действующих на элемент, получим
q dx dy N x0 sin 1 N x0 sin 2 dy N y0 sin 1 N y0 sin 2 dx
N xy0 sin 1 N xy0 sin 12 dx N xy0 sin 1 N xy0 sin 12 dy
Для малых прогибов и углов α и β и учитывая что sin tg
w
, 2 1 1 dx,
x
x
w
1
, 2 1 1 dy,
y
y
12 1 1 dy, 12 1 1 dx.
y
x
1
sin tg

5.

2
2w
2w
0
0 w
q N 2 N xy
Ny 2
x y
x
y
0
x
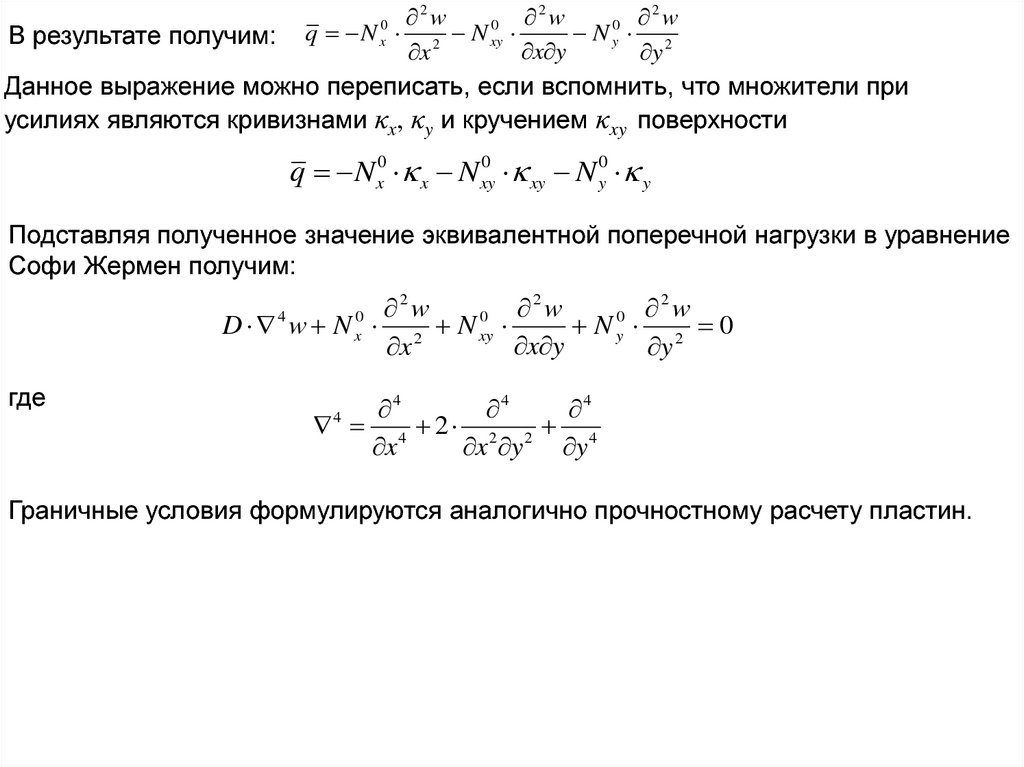
В результате получим:
Данное выражение можно переписать, если вспомнить, что множители при
усилиях являются кривизнами κх, κy и кручением κxy поверхности
q N x0 x N xy0 xy N y0 y
Подставляя полученное значение эквивалентной поперечной нагрузки в уравнение
Софи Жермен получим:
2
2w
2w
0
0 w
D w N 2 N xy
Ny 2 0
x y
x
y
4
где
0
x
4
4
4
4 2 2 2 4
x
x y y
4
Граничные условия формулируются аналогично прочностному расчету пластин.

6.

Полная энергия рассматриваемой пластины будет равна Э U A .
В данном равенстве потенциальная энергия деформации и работа внутренних сил
упругости определяются соотношениями:
2
2
2
2
2
2
2
2
1
w
w
w w
w
dx dy
U D 2 2 2 2 2 2 1
2
x y
x y
x y
2
2
1
w w
0 w
0
0 w
A N x 2 N xy
N y dx dy
2
x y
x
y

7.

1.2. Устойчивость прямоугольной пластины, сжатой в одном
направлении
Рассмотрим сначала прямоугольную
шарнирно опертую пластину, сжатую в
направлении оси х. Разрешающее
уравнение в данном случае имеет вид:
2w
D w N 2 0
x
4
0
x
Граничные условия:
2
w
Решение, удовлетворяющее этому
при x 0 и x a w 0;
0,
2
x
уравнению и граничным условиям
шарнирного опирания будем искать в форме
2w
при y 0 и y b w 0;
0.
2
двойного тригонометрического ряда.
y
w Amn sin
m 1 n 1
m x
n y
sin
.
a
b
Подставляя выражение для w в разрешающее уравнение, будем иметь:
2
2 2
2 m2
m
n
m x
n y
4
0
A
D
N
sin
sin
0
mn
x
2
a 2 b2
a
a
b
m 1 n 1
Ввиду того, что Атп≠0 (случай Атп=0 соответствует исходной плоской форме
пластины), это равенство возможно только в том случае, когда выражение в
квадратных скобках обращается в нуль.

8.

2
В результате получим:
Откуда: N x0
m2 n2 2 m2
4
D 2 2
N x0 0
2
b
a
a
2 a2 D m2
n2
2 2
b
a
m2
2
Представляет интерес наименьшее (критическое) значение усилия. Как видно из
последнего выражения, для этого нужно принять n=1, тогда:
N кр
2 a2 D m2
m2
1
2 2
b
a
mb a
k
a
mb
2
или N кр k
2 D
b2
2
- коэффициент, зависящий от геометрии пластины и ее формы
при потере устойчивости. На рисунке приведены графики,
построенные для различных значений т и a/b.
При заданном значении a/b число т,
характеризующее форму пластины при потере
устойчивости, будет таким, при котором kσ, а
следовательно, и Nкр имеют наименьшее значение.
Соответствующая кривая показана на графике
сплошной линией.

9.

Точки пересечения отдельных ветвей определяются
равенством:
a2
m2
2
m2 1
a2
2 2
b
m 1 2
a
откуда следует формула
m 1 2 1
2
2
b
a
a
m m 1
b
2
т. е.
при 0 a b 2 m 1 и пластина теряет устойчивость по одной полуволне,
при 2 a b 6 m 2 и т. д.
Из рис следует, что для длинных пластин (a/b≥3) можно принять kσ=4.
E h3
Принимая в равенстве
2 D
D
N кр кр h
N кр k 2
12 1 2
b
и то, что для большинства металлов μ=0,3, получим формулу для критических
2
2
напряжений:
h
h
кр 0,9 k E 3,6 E
b
b
широко используемую на практике для оценочных расчетов.
2
2
D
1
a
Формулу для Nкр можно представить в виде (при n=1) N кр
m
2
2
mb
a
Тогда первый член в скобках определяет критическую силу для полосы длиной а и
шириной единица, а второй множитель показывает, во сколько раз целая пластина,
т. е. система связанных полос, более устойчива, чем изолированная полоса.
2

10.

Если ширина пластины велика по сравнению с длиной (a/b<<1), то форма
пластины при потере устойчивости имеет вид цилиндрической поверхности. В этом
случае следует принять т=1 и формула дает
3 E
h3
N кр
2
2
12 1 a
что соответствует формуле Эйлера для критической силы при сжатии стержня
единичной ширины, толщины h и имеющего приведенный модуль упругости
E/(1-μ2)

11.

Рассмотрим устойчивость защемленной
по контуру пластины.
Уравнение устойчивости сохраняет
прежнюю форму
2
4
0 w
D w Nx 2 0
x
а граничные условия принимают вид
при x=0 и x=a w=dw/dx=0,
при y=0 и y=b w=dw/dy=0.
Ввиду того, что построение точного решения этой задачи связано с большими
трудностями, получим приближенное решение, воспользовавшись методом
Бубнова—Галеркина. Прогиб пластины зададим в виде w(x,y)=C·φ(x,y),
где С — неизвестный коэффициент, а 1 cos 2 x / a 1 cos 2 y / b — функция,
удовлетворяющая граничным условиям.
Уравнение метода Бубнова—Галеркина, в рассматриваемом случае имеет вид
a b
L C x, y dx dy 0
0 0
где L(С·φ) есть результат подстановки w=С·φ в уравнение устойчивости
пластины, т. е.
2
2
2 4
2 x
2 y
2 x
2 y
2 2
L C C D
1 cos
cos
cos
2
cos
a
b
a
b
a b
a
4
2
2 y
2 x
2 x
2 y
2
0 2
1 cos
1 cos
cos
C N x
cos
b
b
a
a
a
b

12.

Подставляя в данное выражение и функцию φ в уравнение Бубнова-Галеркина и
выполняя интегрирование, получим
4
2
2
4
2
2 2 2
3 2
3 2
0 3 2
C D N x a b 0
4 a b
4 b
4 a
4 a
Поскольку С≠0 имеем
N N кр k
0
x
где
2D
b2
4 b2
a2
k 3 2 2 3 2
3 a
b
В частности, для квадратной пластины kσ =10,67, что отличается от точного
решения на 5,5 %.
Сравнивая формулы для разного вида закрепления, можно убедиться в том, что
они отличаются только выражением для kσ. Этот вывод справедлив и для других
граничных условий — формула для критических напряжений сжатой пластины
всегда может быть представлена в следующих универсальных формах:
кр
2 D
2 E
h
h
k 2
k
0
,
9
k
E
b h
12 1 2 b
b
2
Последнее равенство записано для случая μ=0,3.
2

13.

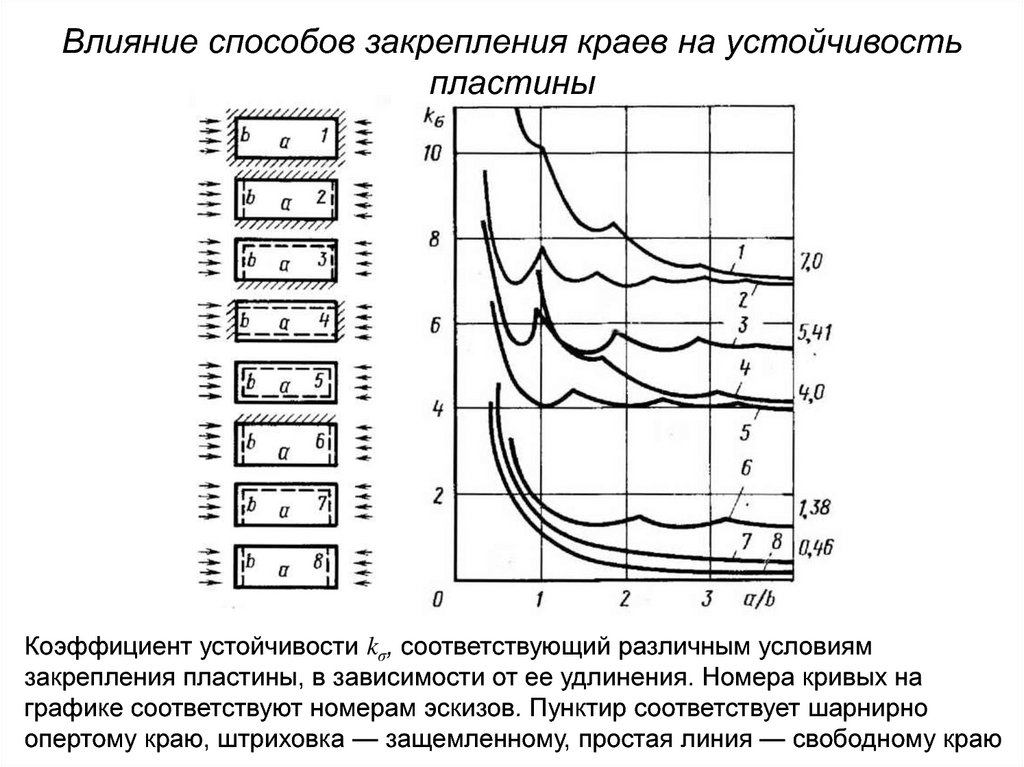
Влияние способов закрепления краев на устойчивость
пластины
Коэффициент устойчивости kσ, соответствующий различным условиям
закрепления пластины, в зависимости от ее удлинения. Номера кривых на
графике соответствуют номерам эскизов. Пунктир соответствует шарнирно
опертому краю, штриховка — защемленному, простая линия — свободному краю

14.

1.3 Устойчивость пластин при сдвиге
В процессе эксплуатации в панелях
крыла летательного аппарата могут
возникать значительные
сдвигающие усилия, вызываемые
перерезывающей силой и крутящим
моментом. Потеря устойчивости,
связанная с действием касательных
напряжений или усилий,
сопровождается образованием в
пластине прогиба в виде системы
косых волн.
Уравнение устойчивости в
рассматриваемом случае принимает вид:
2w
D w 2 N
0
x y
4
0
xy
Форма потери устойчивости пластины при
сдвиге:
1 — выпуклость; 2 — впадина; 3 узловая
линия

15.

Точное решение этого уравнения даже для пластин с шарнирно опертыми краями
представляет большие трудности. Поэтому рассмотрим приближенное решение,
основанное на методе Ритца—Тимошенко и справедливое для пластин с большим
удлинением (a>>b). Зададим прогиб в следующей форме, аппроксимирующей
систему косых волн
w C sin
y
b
sin
l
x k y .
Такое представление удовлетворит
только условию по прогибу на
длинных сторонах, т. е. w(x,0)=0;
w(x.b)=0. Условия на коротких
сторонах x=0 и x=a не
выполняются, что для длинной
пластины не очень существенно.
Из принятой для прогиба зависимости следует, что прогиб обращается в нуль на
косых узловых линиях x k y 0 , наклоненных к оси х под углом arc ctg k .
Для реализации метода Ритца—Тимошенко найдем потенциальную энергию U и
работу внешних сил А. Осуществляя интегрирование по параллелограмму,
заштрихованному на рисунке т. е. по x от ky до l+ky, а по y от 0 до b, получим
U
2
4 C 2 D l
8 b l
2
b
2 2
6 k 2 1 k ,
l
b
2
A N
0
xy
2 C2 k
4 l

16.

Критическое усилие определяется из условия U=А. Приравнивая выражения и
выражая напряжение через усилие имеем:
xy
где
k
N xy0
h
k
2 D
b2 h
2
1
1
l
6 k 2 2 l 2 2 1 k 2 , l
2 k
b
l
Величина kτ зависит от двух параметров l и k. Минимизируя kτ по l
т.е. используя условие , k l 0 получим l 2 1 k .2
Подставляя в kτ и записывая условие минимума по k, т е., k k 0 найдем k 2 2 .
Таким образом, arcctg k 540 44 , l 1,22 и k 4 2 5,66. После подстановки
получим приближенное выражение для критических касательных напряжений:
кр 5,66
2 D
Оно превышает точное значение на 6 %.
b2 h

17.

Для пластины с конечным соотношением сторон решение в принципе можно
задать в форме двойного тригонометрического ряда
m x
n y
w Amn sin
m 1 n 1
a
sin
b
.
Каждый член этого ряда удовлетворяет условиям шарнирного опирания, однако,
для того чтобы описать таким образом систему косых волн, требуется удержать
большое количество членов разложения. В отличие от задачи, рассмотренной
ранее, в данном случае непосредственная подстановка ряда в уравнение
2w
устойчивости
4
0
D w 2 N xy
x y
0
не позволяет тождественно удовлетворить его за счет соответствующего выбора
N0xy, поскольку четные производные будут содержать произведения синусов, а
смешанная 2 w x y — произведение косинусов. В связи с этим воспользуемся
для решения методом Ритца—Тимошенко. Подставляя разложение для прогиба
w в формулы для U и A, приведенные в общих соотношениях и учитывая
соотношения
a
a / 2 при m i
m x
i x
sin
dx
0 при m i
0
b
b / 2 при n j
n y
j y
sin
sin
dy
0
b
b
0 при n j
i
a
2 a
i x
j x
2
при m i - нечетное
2
sin
cos
dx
i
m
0
a
a
0
при m i - нечетное
a
sin
a

18.

получим
2
m2 n2
2
U
a b D Amn 2 2 ,
8
b
m 1 n 1
a
A Aij m n i j
A 4 N xy0 mn
m2 i 2 j 2 n2
m n
i
j
4
В разложении для A учитываются только те сочетания индексов, для которых
суммы m i и n j одновременно являются нечетными. В соответствии с
методом Ритца—Тимошенко необходимо записать условия минимума полной
энергии Э U A в виде Э Amn 0 . В результате получим следующую систему
однородных алгебраических уравнений относительно Amn:
4
m2 n 2
m n i j
D a b Amn 2 2 8 N xy0 Aij 2 2 2
0,(m, n 1,2,3....)
2
4
a
b
m
i
n
j
i
j
Здесь суммы m+i и n+j должны быть нечетными. Задавая различные наборы
комбинаций mn (например — 11, 12, 21, 22 и т. д.) и приравнивая нулю
определитель, составленный из коэффициентов уравнений, можно получить
характеристическое уравнение, наименьший корень которого определяет
критическое усилие сдвига.

19.

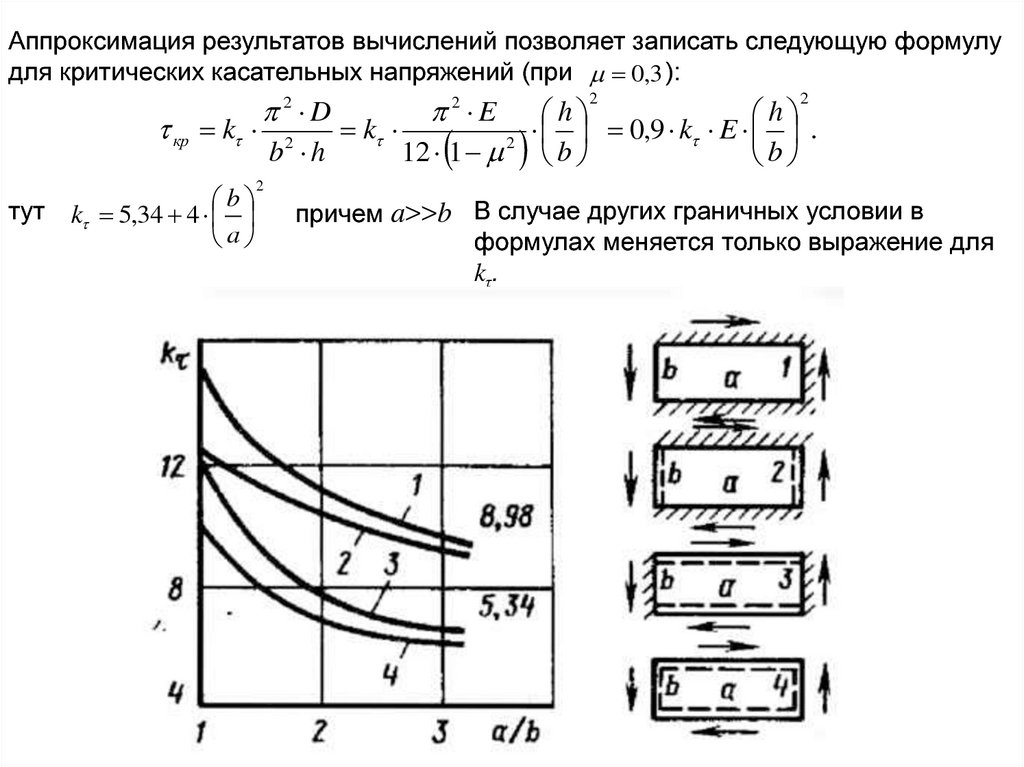
Аппроксимация результатов вычислений позволяет записать следующую формулу
для критических касательных напряжений (при 0,3 ):
2 D
2 E h
h
кр k 2
k
0
,
9
k
E
.
2
b h
12 1 b
b
тут
b
k 5,34 4
a
2
2
2
причем a>>b В случае других граничных условии в
формулах меняется только выражение для
k τ.

20.

2. Устойчивость пластин при комбинированном нагружении
Рассмотрим случаи, когда отличными от
нуля оказываются два докритических
усилия.
Пусть шарнирно опертая пластина
сжимается в двух направлениях
Совместно действующие усилия будем
отмечать верхней чертой. Уравнение
устойчивости будет иметь вид:
2
2
w
w
D 4 w N x0 2 N y0 2 0
x
y
Дальнейший ход решения полностью аналогичен случаю одноосного сжатия.
Задавая прогиб в виде ряда и подставляя его в уравнение устойчивости, получим:
w Amn sin
m 1 n 1
N x0
m x
n y
sin
.
a
b
2
m
m
n
0 n
4
0
N
D
y
2
2
2
2
a
b
b
a
2
2
2
2
2
2

21.

0
0
0
0
Пусть для определенности N x N y . Тогда, обозначив N y N x (причем 1 ),
0
запишем выражение для N x в форме
2
N xкр k min
2 D
b
2
где
2 b2
m 2 n 2
a
k
2
b
m2 2 n2
a
В формулу подставляется найденное в результате подстановки различных
значений т и n минимальное значение k, соответствующее заданной величине φ.
Для получения качественного результата рассмотрим квадратную пластину, т. е.
случай а = b. Тогда
m
k
2
n2
m2 n2
2
и при φ<1 реализуется минимум при т=n=1 т. е. kmin 4 1
Заменим здесь kmin через N xкр с помощью формулы и подставим N yкр N xкр .
Тогда, учитывая, что при раздельном действии усилий их критические значения
для квадратной пластины определяются равенствами:
N xкр N yкр 4
2 D
b2
окончательно получим:
N xкр
N xкр
N yкр
N yкр
1

22.

Графическая интерпретация этого соотношения
представлена на рисунке. Прямая разделяет
область возможных комбинаций усилий N x0 и N y0 на
две части. Комбинации усилий, лежащие в области
1, не вызывают потери устойчивости пластины.
Граничная прямая, т. е. комбинация усилий N xкр и N yкр
соответствует критическому состоянию, а область 2
является областью неустойчивости.
Области устойчивости (1) и
неустойчивости (2) пластинки,
сжатой в двух направлениях

23.

Рассмотрим теперь другой распространенный случай комбинированного
0
0
нагружения — совместное действие сжимающих N x и сдвигающих N xy усилий.
Уравнение устойчивости будет иметь вид:
2w
2w
0
D w N 2 N xy
0
x
x y
4
Тогда, задавая прогиб в форме
0
x
y
w C sin
b
sin
l
x k y .
и повторяя те же выкладки как и в случае потери устойчивости от касательных
напряжений получим:
N xкр 2 N xyкр k
2 D
b2
1
2 2
6 k 2 l 2 1 k
l
2
2
Минимальное значение правой части, как было показано в ранее, реализуется при
l 2 1 k 2. Тогда имеем
N xкр 2 k N xyкр 4
2 D
b
2
1 2 k 2

24.

В соответствии с ранее полученными результатами критические значения отдельно
действующих усилий равны:
2 D
2 D
N xкр 4
b2
, N xyкр 4 2
b2
С учетом этого полученное равенство принимает вид:
N xкр
N xкр
2 2
k N xyкр
N xyкр
1 2 k 2
Применим далее следующий приближенный прием. Зафиксируем величину
касательных усилий и найдем k из условия минимума нормальных усилий, т. е. из
уравнения N xкр k 0 . В результате получим k 2 N
2 N
0
Равенство принимает следующую
окончательную форму:
N xкр
N xкр
N xyкр
Nx
кр
2
1
Графическая интерпретация этого соотношения
представлена на рисунке. Уравнение, включающее
критические комбинации усилий, определяет
границу, отделяющую область устойчивости (1) от
области неустойчивости (2) (сплошная линия)
xy кр
xy кр

25.

Пусть на пластину одновременно действуют докритические усилия . Введем
декартовы оси координат и вдоль каждой из них будем откладывать величины
соответствующих усилий. Тогда любая комбинация усилий будет соответствовать
точке этого пространства. Область, образованная из точек, соответствующих
таким комбинациям усилий, которые не вызывают потери устойчивости
пластины, называется областью устойчивости. Эта область ограничена
поверхностью, которая образована из точек соответствующих критическим
состояниям пластины, и называется поверхностью устойчивости. Очевидно,
что поверхность устойчивости пересекает оси координат в точках ,
соответствующих критическим значениям усилий при их раздельном действии.
Определение поверхности устойчивости является важной, но в то же время и
сложной задачей. Если поверхность устойчивости не определена, то приближенно
предвидеть поведение системы при заданной комбинации усилий можно,
руководствуясь теоремой П. Ф. Папковича о выпуклости поверхности
устойчивости, которая утверждает, что эта поверхность может быть обращена
выпуклостью только в сторону области неустойчивости, т. е. прямая,
соединяющая две точки поверхности, всегда лежит в области устойчивости
(как в случае, показанном на рис.) или принадлежит
граничной поверхности. Таким образом, если бы
мы не располагали уравнением граничной кривой,
показанной на рисунке сплошной линией, о
состоянии системы можно было приближенно
судить по границе, показанной на рисунке.
пунктиром. Если имеется дополнительная
информация, например, о состоянии системы при
воздействии комбинации усилий, соответствующей
точке A, границу области устойчивости можно
уточнить (штрихпунктирная линия на рисунке.

26.

3. Несущая способность систем, состоящих из пластин,
работающих на устойчивость, и стержней
3.1. Панель, подкрепленная стрингерами
Пластины, используемые в конструкциях летательных
аппаратов с целью повышения критической нагрузки,
как правило, подкрепляются системой продольных
элементов — стрингеров.
Однако такое подкрепление не исключает местной
формы потери устойчивости — т. е. выпучивания
панелей обшивки между стрингерами (рис. а).
Это явление необходимо учитывать при расчете и
конструировании панели.
В докритическом состоянии напряжения
распределяются равномерно по ширине
панели (рис. б) и определяются равенством:
0
N b
b h 2 f ст

27.

При возрастании внешнего распределенного усилия N
напряжения σ0 в пластине достигают критического
значения, определяемого формулой
кр
h
3,6 E
b
2
и пластина теряет устойчивость. Усилие, при котором
это происходит, можно найти, если принять σ0=σкр, т.е
f
N кр кр h 2 ст
b
При N>Nкр нагрузка воспринимается в основном
стрингерами, однако пластина также продолжает
работать. Примерное распределение напряжений в ней
показано на рис.в сплошной линией.
В средней части пластины напряжения сохраняются на уровне σкр, а вблизи
стрингеров, с которыми она связана, напряжения, очевидно, будут близки к
напряжениям в стрингере σст. Для того чтобы определить восприятие нагрузки
пластиной после потери устойчивости, необходимо знать точный закон
распределения напряжений, который можно найти только в результате решения
сложной нелинейной задачи о закритическом поведении пластины. Для
приближенной оценки этого вклада можно попытаться осреднить это неизвестное
распределение по ширине пластины (пунктирная линия на рис. в).

28.

Различные под ходы к решению рассматриваемой
задачи различаются способами такого осреднения.
Наиболее близким к экспериментальным данным из
них оказался подход, предложенный Т. Карманом и
основанный, по существу, на определении среднего
напряжения по правилу среднего геометрического, т. е.
ср кр ст
Таким образом, доля усилия, воспринимаемого
обшивкой, равна σcp∙b. Ввиду того, что основную роль в
восприятии внешней нагрузки играют стрингеры,
приведем обшивку к стрингерам т. е. будем условно
считать в соответствии с рис. г, что в полосках шириной
bпр 2 напряжения в обшивке равны σст, а в средней
части они вообще отсутствуют.
Тем самым обшивка заменяется двумя полосками с приведенной шириной,
которые присоединяются к стрингерам. Условие эквивалентности такой замены
имеет вид ср b ст bпр . Отношение bпр b , показывающее, на какой
относительной ширине обшивку можно считать работающей с напряжениями,
равными напряжению в стрингере, называется редукционным коэффициентом по
устойчивости. На основании определения редукционного коэффициента получим
bпр
b
ср
кр
h
E
1,9
ст
ст
b ст

29.

Усилие, воспринимаемое подкрепленной панелью, определяется, таким образом,
равенством:
f
N ст h 2 ст
b
Для определения предельного усилия необходимо в соответствии с возможной
формой разрушения стрингера задать σст (этот вопрос рассматривается в курсах
прочности летательных аппаратов), а далее по формулам найти φ и Ν.
В случае, если обшивка и стрингер изготовлены из различных материалов с
модулями упругости E0 и Eст, необходимо сначала произвести редуцирование по
материалу и ввести условную (редуцированную) площадь сечения стрингера fр и
условные напряжения в нем σp, т. е.
E
E
,
f p f ст ст
p ст ст
E0
E0
Стрингер такими параметрами можно условно считать изготовленным из
материала с модулем упругости Е0 и использовать для расчета панели полученные
выше соотношения. В частности, если заменить в формуле для докртических
напряжений в обшивке σ0 параметры на редуцированные получим
0
N b E0
,
E0 b h 2 Eст f cт
0
ст
N b Eст
E0 b h 2 Eст f cт

30.

Критическое значение величины внешнего усилия, вызывающего потерю
устойчивости обшивки:
2 f ст Eст
N кр кр h
b
E0
Здесь σκρ определяется по приведенной выше формуле при Е=Е0. Формула для
редукционного коэффициента φ преобразуется к следующему виду
кр E 0
b
ст E ст
bпр

31.

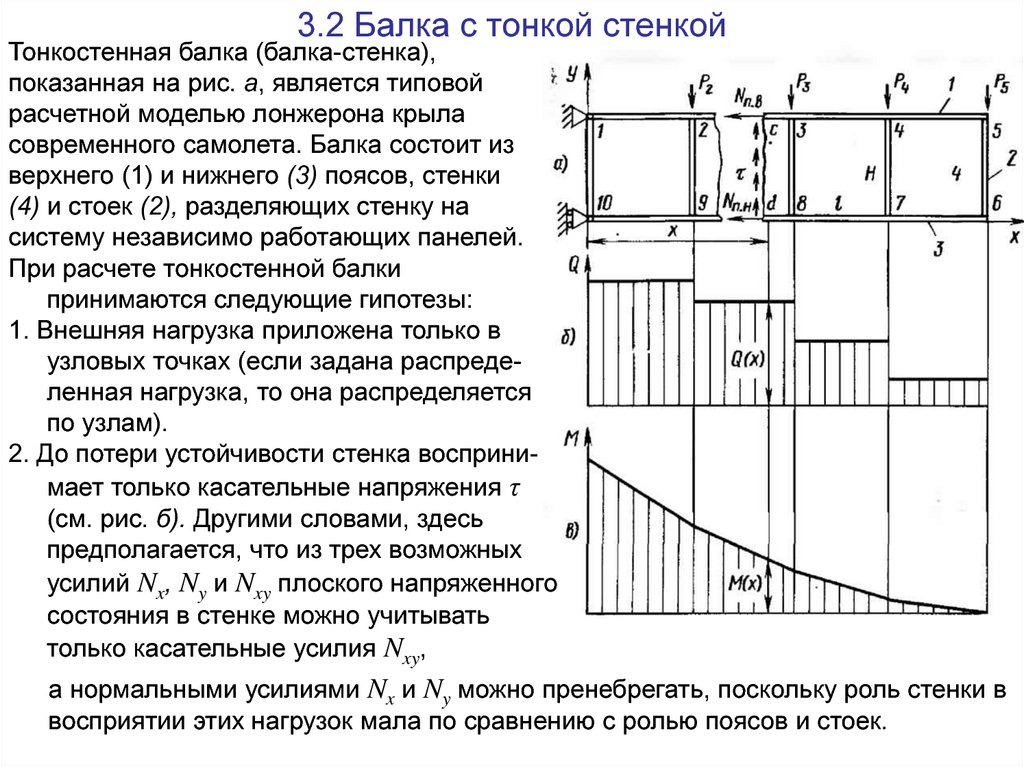
3.2 Балка с тонкой стенкой
Тонкостенная балка (балка-стенка),
показанная на рис. а, является типовой
расчетной моделью лонжерона крыла
современного самолета. Балка состоит из
верхнего (1) и нижнего (3) поясов, стенки
(4) и стоек (2), разделяющих стенку на
систему независимо работающих панелей.
При расчете тонкостенной балки
принимаются следующие гипотезы:
1. Внешняя нагрузка приложена только в
узловых точках (если задана распределенная нагрузка, то она распределяется
по узлам).
2. До потери устойчивости стенка воспринимает только касательные напряжения τ
(см. рис. б). Другими словами, здесь
предполагается, что из трех возможных
усилий Nx, Ny и Nxy плоского напряженного
состояния в стенке можно учитывать
только касательные усилия Nxy,
а нормальными усилиями Nx и Ny можно пренебрегать, поскольку роль стенки в
восприятии этих нагрузок мала по сравнению с ролью поясов и стоек.

32.

На основании второй гипотезы N x N y 0
Уравнения равновесия приобретают вид:
0
N yx0
N x0 N yx
0
0
x
y
y
N y0
N xy0
0
N xy0
0
y
x
x
т.е. N xy const , и, следовательно,
касательные напряжения N xy h
(h — толщина стенки) в пределах панели
постоянны.
3. Пояса и стойки до потери устойчивости
стенки работают только на растяжение
или сжатие.
С учетом принятых гипотез тонкостенная
балка оказывается статически определимой,
т. е. усилия и напряжения во всех ее
элементах могут быть найдены из
уравнений равновесия.
Рассмотрим некоторое сечение cd x=const (см. рис. а), в котором внешние силы
образуют поперечную силу Q(х) и изгибающий момент М(х) (см. рис. б, в), и
запишем условия равновесия отсеченной части балки. Проектируя все
Q x
действующие силы на ось у, получим τ∙h∙H=Q(х), откуда:
h H

33.

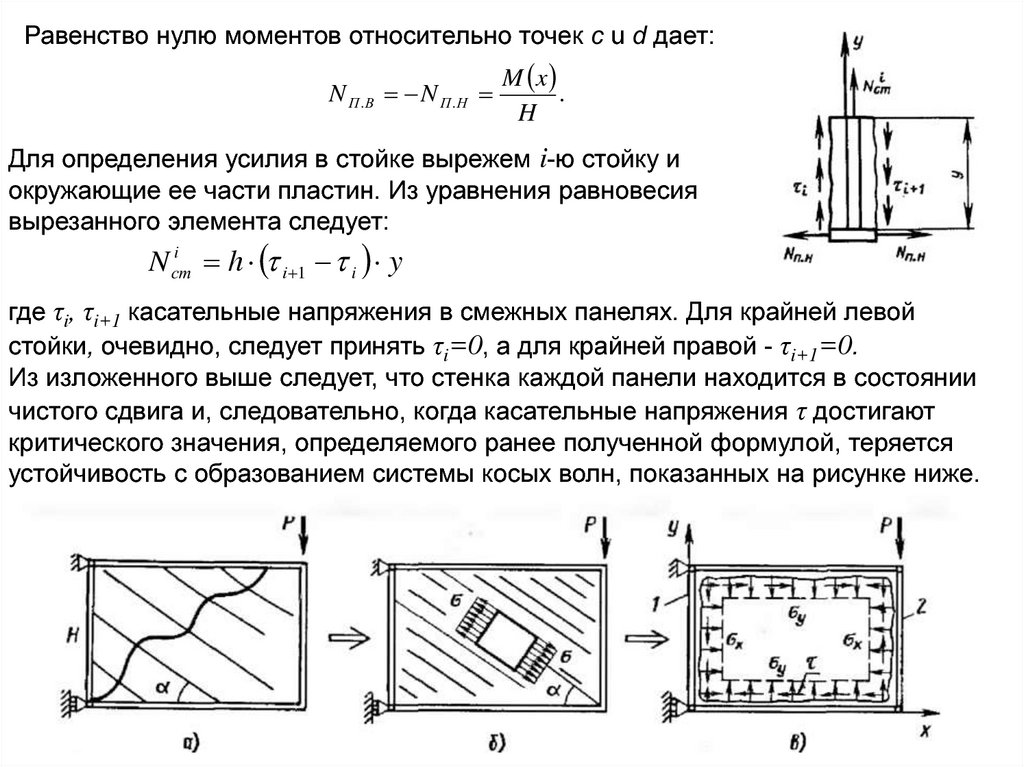
Равенство нулю моментов относительно точек c u d дает:
N П .В N П .Н
M x
.
H
Для определения усилия в стойке вырежем i-ю стойку и
окружающие ее части пластин. Из уравнения равновесия
вырезанного элемента следует:
i
N ст
h i 1 i y
где τi, τi+1 касательные напряжения в смежных панелях. Для крайней левой
стойки, очевидно, следует принять τi=0, а для крайней правой - τi+1=0.
Из изложенного выше следует, что стенка каждой панели находится в состоянии
чистого сдвига и, следовательно, когда касательные напряжения τ достигают
критического значения, определяемого ранее полученной формулой, теряется
устойчивость с образованием системы косых волн, показанных на рисунке ниже.

34.

Для тонких стенок τкр оказывается довольно малой величиной и при дальнейшем
возрастании нагрузки балка работает со стенкой, потерявшей устойчивость.
Строгий анализ поведения конструкции при этом требует решения исключительно
сложной нелинейной задачи о закритической деформации пластины при сдвиге,
однако приближенное решение может быть построено на основании гипотезы о
существовании в стенке после потери устойчивости «диагонального» поля
растягивающих напряжений. Очевидно, что после образования системы косых
волн (рис. а) стенка в основном воспринимает нагрузку за счет растягивающих
напряжений, параллельных гребням волн. В связи с этим будем считать, что
стенка находится в состоянии одноосного растяжения под углом α по отношению к
поясам (см. рис. б).
Эти напряжения, в свою очередь, можно привести к самоуравновешенной системе,
напряжений σx, σy, τxy показанной на рис. в.

35.

Для того чтобы это сделать,
выделим из стенки два элемента,
показанных на рис., и рассмотрим
их равновесие.
Проектируя силы, действующие
на элемент 1, на оси х и у и
учитывая, что напряжения σ
распределены по площадке со
стороной dx·sinα, получим
Аналогично для элемента 2
cos dy cos x dy 0
sin dy cos dy 0
cos dx sin dx 0,
sin dx sin y dx 0,
После сокращения на dx и dy первое и последнее равенства одинаковые, поэтому
в итоге имеем три соотношения:
sin cos
y sin 2
x cos 2
Выражая из первого равенства σ и подставляя во второе и третье, получим:
2
, x ctg
2
sin
y tg

36.

Из рис. в следует, что, рассматривая равновесие отсеченной части балки и
проектируя все силы на ось у, получим для τ прежнюю формулу. Таким образом,
окончательно имеем :
2 Q
Q
Q
σ
,
σ
ctg
,
σ
tg
x
y
h H sin 2
h H
h H
Рассмотрим определение угла α. Из рис. в следует, что в результате потери
устойчивости стенки напряжения σx и σy догружают пояса и стойки, уже имеющие
усилия, вызванные внешней нагрузкой, дополнительными сжимающими силами.
Поскольку эти напряжения равномерно распределены по длине и ширине панели,
будем иметь:
1
2
N ст
N ст
0,5 y h l
N П .В N П .Н 0,5 x h H
Таким образом, для балки, показанной на рис.в, получаем M P l x
P H h

37.

Выражаем усилия в поясах и стойках:
P
P
P
P
l x
, N П .В l x
,
H
2 tg
H
2 tg
y
l
y
l
2
P
tg , N ст
P
tg ,
H 2 h
H 2 h
N П .В
1
N ст
Напряженное состояние стенки, поясов и стоек, определяемое полученными
соотношениями, при произвольном α удовлетворяет всем уравнениям равновесия,
т. е. является статически возможным. Как следует из принципа наименьшей
работы, истинное напряженное состояние можно выделить из всех статически
возможных, записав условие минимума дополнительной потенциальной энергии
системы U .
В рассматриваемом случае U складывается из энергии обшивки, поясов и стоек:
1
U U 0 U П . В U П . Н U ст
U ст2
2
l
l
l
2
l
2
1
2
N П2 . В
N П2 . Н
N ст
N ст
h H l
dx
dx
dy
dy
2 E0
2 E П FП
2 E П FП
2 Eст Fст
2 Eст Fст
0
0
0
0
Здесь E0 , E П , Eст— модули упругости материала обшивки, поясов и стоек;
FП , Fст — площади сечения поясов и стоек.

38.

Подставляя σ и усилия, после интегрирования получим:
P2 l
1
2 l2 h
h H ctg 2 h l tg 2
2 H 2 h
U
2
2
2 H h E0 sin cos 3 H FП EП
2 FП EП
2 Fст Eст 3 l Fст Eст
Условие минимума U имеет вид U 0 . Окончательно после некоторых
преобразований из этого условия получим
1 П
H h E0
l h E0
tg 4
П
, ст
где
1 ст
2 E П FП
2 Eст Fст
Полученная формула, выведенная для балки с одной стенкой, приближенно
считается справедливой и в общем случае, т. е. используется для определения
угла наклона волн в отдельных панелях тонкостенной балки.
Таким образом, усилия в поясах и стойках могут быть найдены с помощью
полученных выше равенств, определяющих составляющие усилий,
образовавшиеся до потери устойчивости стенки, и равенств, определяющих
дополнительные сжимающие составляющие, образовавшиеся в результате потери
устойчивости стенки.

39.

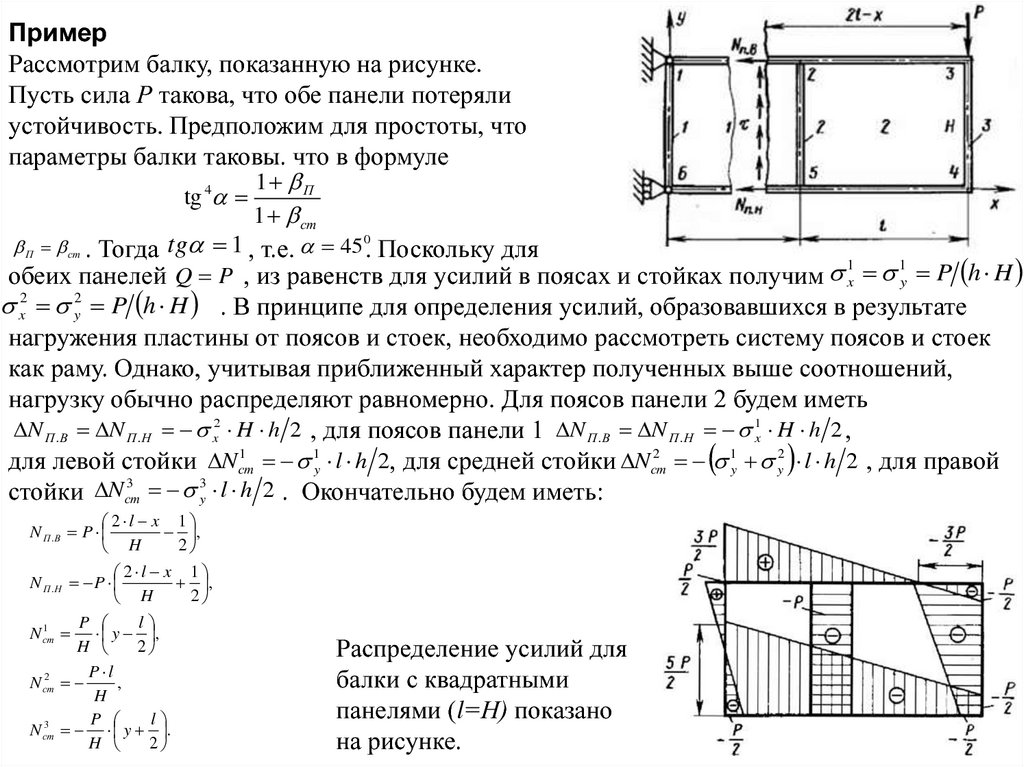
Пример
Рассмотрим балку, показанную на рисунке.
Пусть сила Р такова, что обе панели потеряли
устойчивость. Предположим для простоты, что
параметры балки таковы. что в формуле
1 П
tg 4
1 ст
П ст . Тогда tg 1 , т.е. 45 0. Поскольку для
1
1
обеих панелей Q P , из равенств для усилий в поясах и стойках получим x y P h H
x2 y2 P h H . В принципе для определения усилий, образовавшихся в результате
нагружения пластины от поясов и стоек, необходимо рассмотреть систему поясов и стоек
как раму. Однако, учитывая приближенный характер полученных выше соотношений,
нагрузку обычно распределяют равномерно. Для поясов панели 2 будем иметь
N П .В N П .Н x2 H h 2 , для поясов панели 1 N П .В N П .Н 1x H h 2 ,
1
2
1y l h 2, для средней стойки N ст
1y y2 l h 2 , для правой
для левой стойки N ст
3
3
стойки N ст y l h 2 . Окончательно будем иметь:
2 l x 1
N П .В P
,
2
H
2 l x 1
N П .Н P
,
2
H
P
l
y ,
H
2
P l
,
H
P
l
y .
H
2
1
N ст
2
N ст
3
N ст
Распределение усилий для
балки с квадратными
панелями (l=Н) показано
на рисунке.