Похожие презентации:
Расчет потенциалов простейших электростатических полей
1.
Лекция 6. Расчет потенциалов простейшихэлектростатических полей
6.1. Уравнения Лапласа и Пуассона
6.2. Силовые линии и эквипотенциальные
поверхности
6.3. Расчет потенциалов простейших
электростатических полей
2.
6.1. Уравнения Лапласа иЧасто предпочтительнымПуассона
методом нахождения Е является
сведение задачи к решению дифференциального уравнения для
потенциала.
Теорема Гаусса: E ρ ε 0 и E - следовательно
2 - ρ ε 0 2 - оператор Лапласа (лапласиан)
div grad 2
2x 2y 2z
2
x
2
2
y
2
2
z 2
2 ρ ε 0 - уравнение Пуассона
В области пространства, где заряды отсутствуют =0
0
2
- уравнение Лапласа
3.
Рассмотрим несколько примеров вычисленияразности потенциалов между точками поля,
созданного некоторыми заряженными телами
4. 6.2. Силовые линии и эквипотенциальные поверхности
Направление силовой линии (линии напряженности)в каждой точке
совпадает с направлением
. E
Отсюда следует, что напряженность равна разности
потенциалов U на единицу длины силовой линии.
Именно вдоль силовой линии происходит максимальное изменение
потенциала. Поэтому всегда можно определить
между двумя точками, измеряя U между ними, причем
тем точнее, чем ближе точки.
В однородном электрическом поле силовые линии – прямые.
Поэтому здесь определить E наиболее просто:
(5.6.1)
φ
U
E
l
5.
Воображаемая поверхность, все точки которойимеют одинаковый потенциал, называется
эквипотенциальной поверхностью.
Уравнение этой поверхности
(6.6.2)
φ φ( x, y, z ) const.
6.
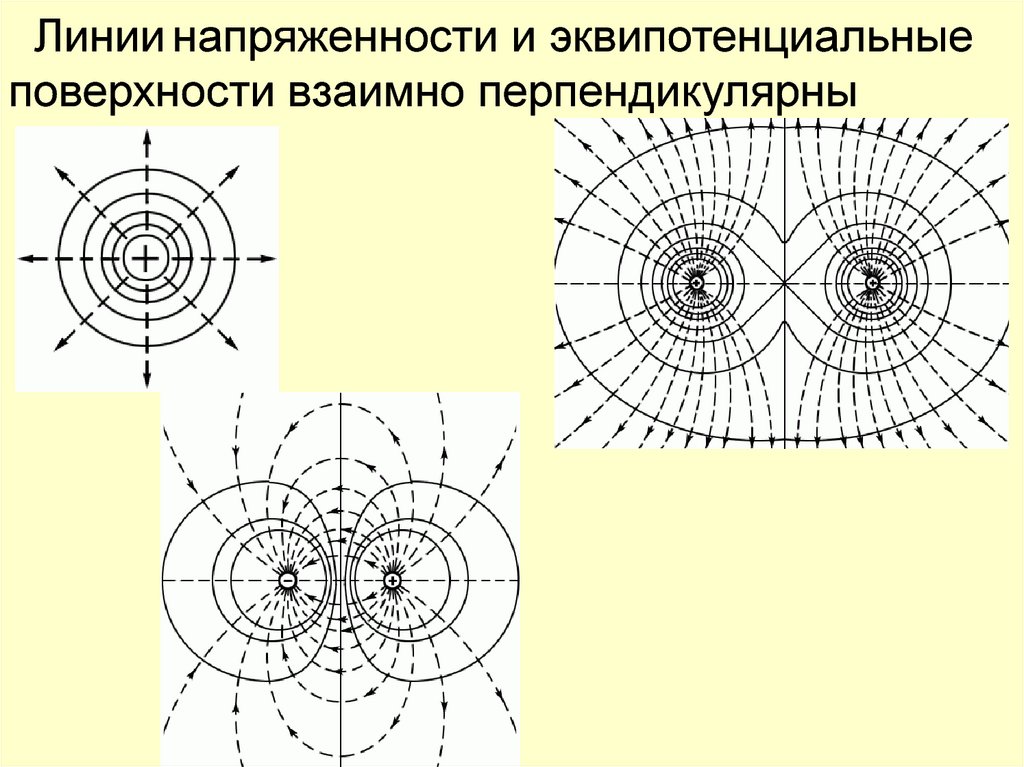
Линии напряженности и эквипотенциальныеповерхности взаимно перпендикулярны
7.
Формула E grad φвыражает связь
потенциала с напряженностью и позволяет по
известным значениям φ найти напряженность
поля в каждой точке.
Можно решить и обратную
задачу, т.е. по
известным значениям E в каждой точке поля
найти разность потенциалов между двумя
произвольными точками поля.
φ1 φ 2 (E, d l ).
2
1
8.
φ1 φ 2 (E, d l ).2
1
Интеграл можно брать по любой линии,
соединяющие точку 1 и точку 2, ибо работа сил
поля не зависит от пути.
Для обхода по замкнутому контуру φ1 φ 2получим:
т.е. пришли к известной нам теореме о циркуляции
вектора напряженности: циркуляция вектора
напряженности электростатического поля
вдоль любого замкнутого
контура равна нулю.
(
E
,
d
l
)
0
,
Поле, обладающее этим свойством, называется потенциальным.
9.
• Из обращения в нуль циркуляции вектораследует, что линии электростатического
поля не могут быть замкнутыми: они
начинаются на положительных зарядах
(истоки) и на отрицательных зарядах
заканчиваются (стоки) или уходят в
бесконечность
10.
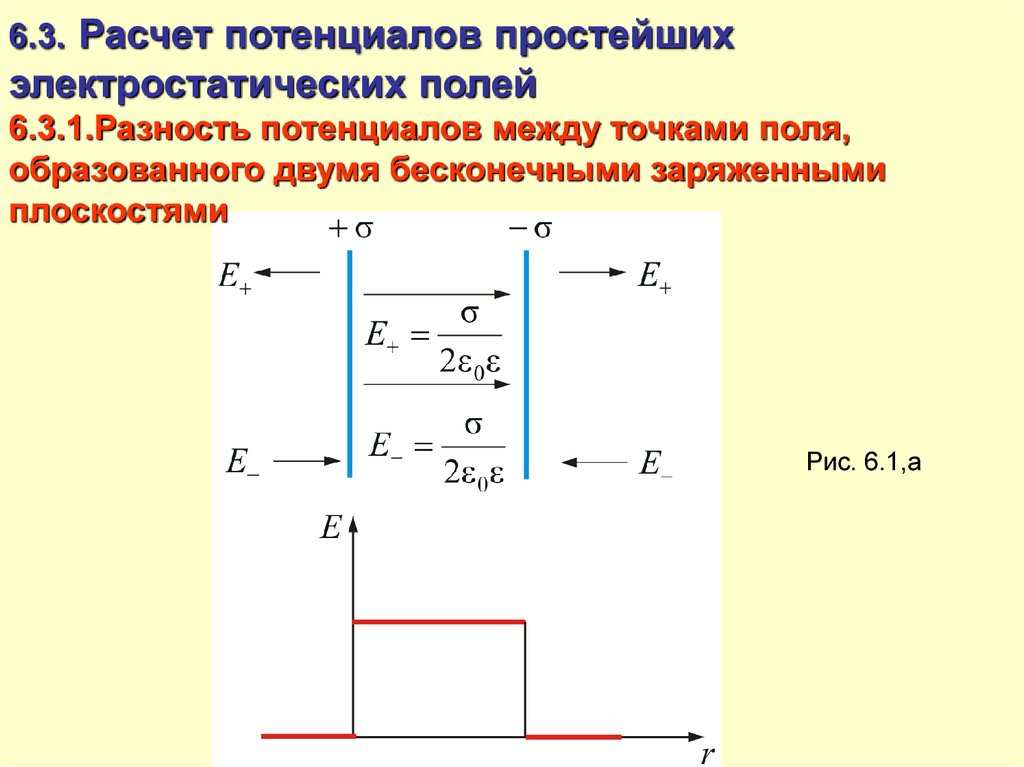
6.3. Расчет потенциалов простейшихэлектростатических полей
6.3.1.Разность потенциалов между точками поля,
образованного двумя бесконечными заряженными
плоскостями
Рис. 6.1,а
11.
Мы показали, что напряженность связана спотенциалом
dφ
тогда dφ Edl
E
,
(6.1.1)
dl
σ
E
где
ε0
– напряженность
электростатического поля между заряженными
плоскостями
σ = q/S – поверхностная плотность заряда.
12.
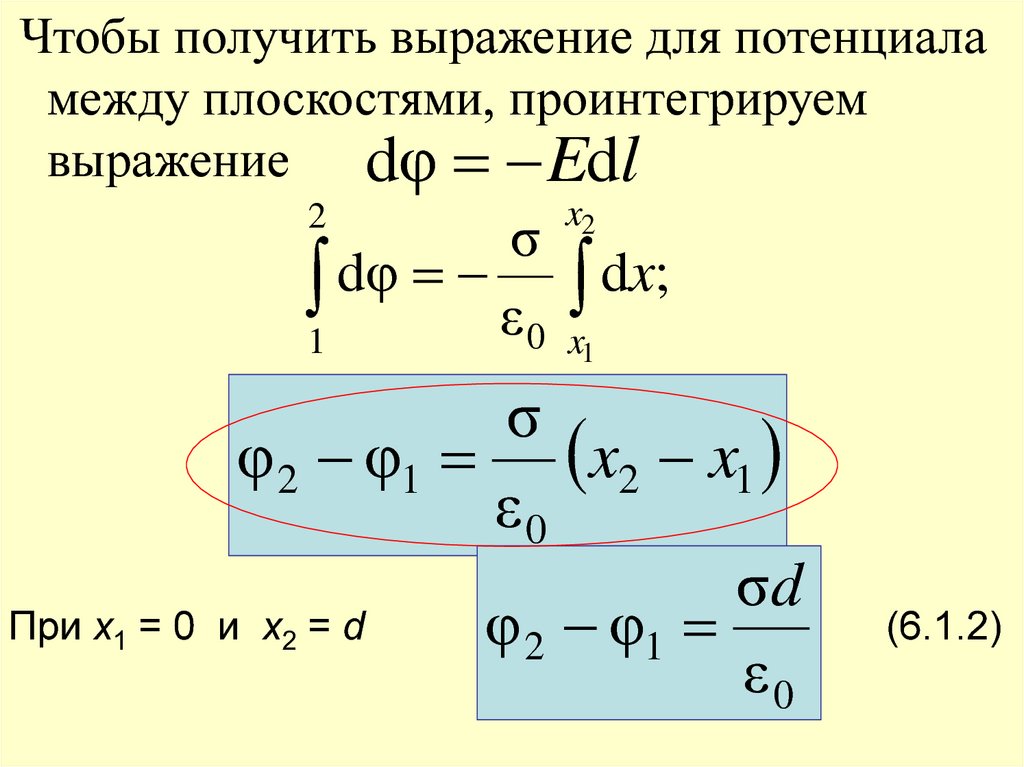
Чтобы получить выражение для потенциаламежду плоскостями, проинтегрируем
выражение dφ Edl
2
x2
σ
dφ ε 0 dx;
1
x1
При x1 = 0
σ
φ 2 φ1 x2 x1
ε0
σd
и x2 = d
φ 2 φ1
ε0
(6.1.2)
13.
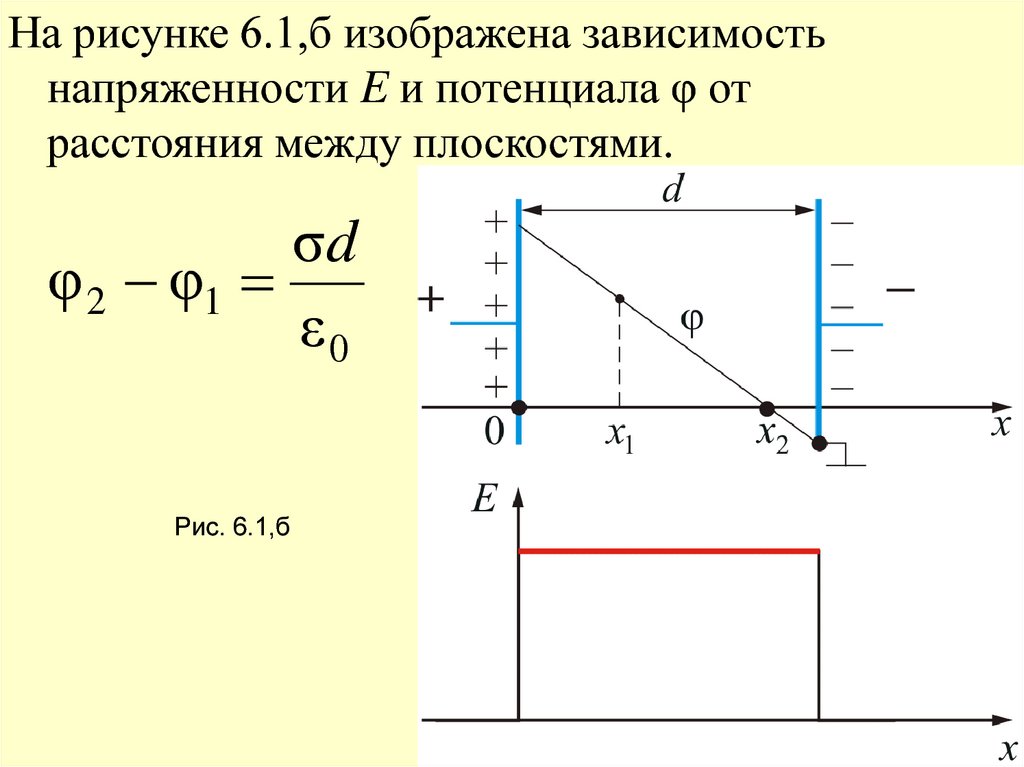
На рисунке 6.1,б изображена зависимостьнапряженности E и потенциала φ от
расстояния между плоскостями.
σd
φ 2 φ1
ε0
Рис. 6.1,б
14. 6. 3.2. Разность потенциалов между точками поля, образованного бесконечно длинной цилиндрической поверхностью
С помощью теоремы Остроградского-Гауссамы показали, что
0
внутри
цилиндра,
т.к.
там
нет
зарядов
λ
q
E
или
на поверхности цилиндра
2
πε
R
2
πε
Rl
0
0
λ
q
или
вне цилиндра.
2 πε0 rl
2 πε0 r
15.
Тогда, т.к.dφ Edr;
2
λ
dφ 2 πε 0
1
r2
r1
dr
r
отсюда следует, что разность потенциалов в
произвольных точках 1 и 2 будет равна:
r2
q
r2
2 1
ln
ln .
2 0 r1
2 0l r1
1
2 ln R const внутри и на поверхности
0
цилиндра
r
ln
вне цилиндра.
2 0 R
16.
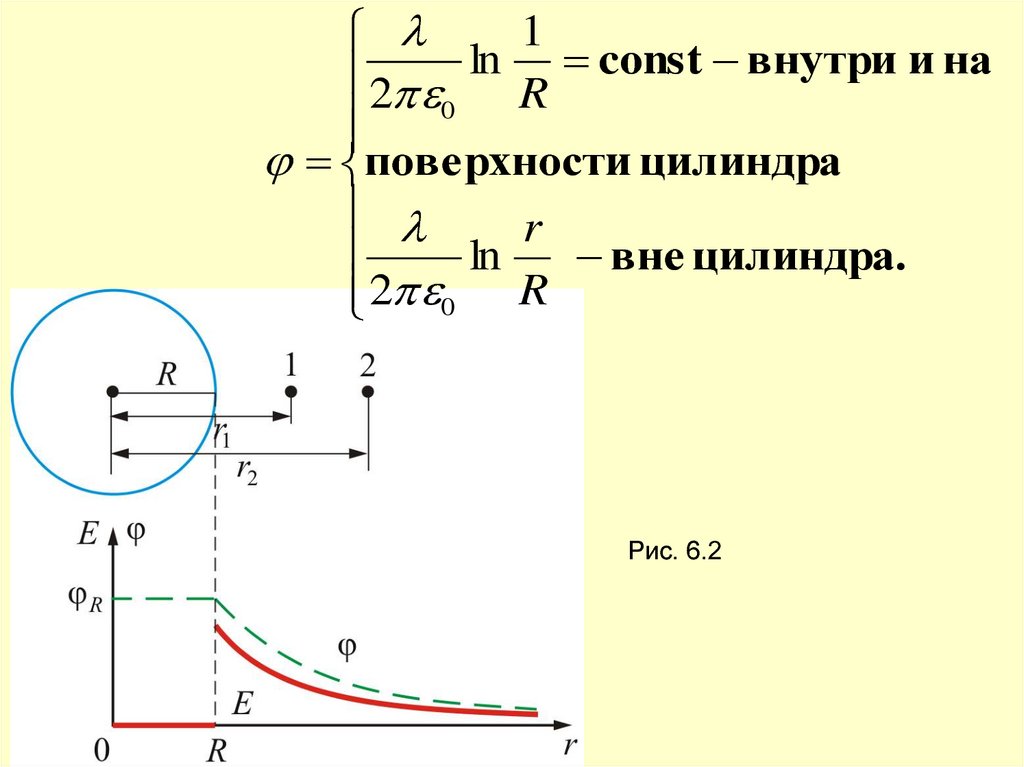
12 ln R const внутри и на
0
поверхности цилиндра
r
ln
вне цилиндра.
2 0 R
Рис. 6.2
17. 6.3.3. Разность потенциалов между обкладками цилиндрического конденсатора
Рис. 6.30 внутри меньшего
и вне большего цилиндров зарядов нет
E
между
цилиндрами
,
2 r
0
когда R1 r R2 .
18.
Т.к.dφ Edr
, то
λ
r2
φ 2 φ1
ln
2πε0 r1
R2
2 ln R const внутри меньшего
0
1
цилиндра ( r R1 )
ln r между цилиндрами ( R r R )
1
2
2 0 R1
0 вне цилиндров.
19.
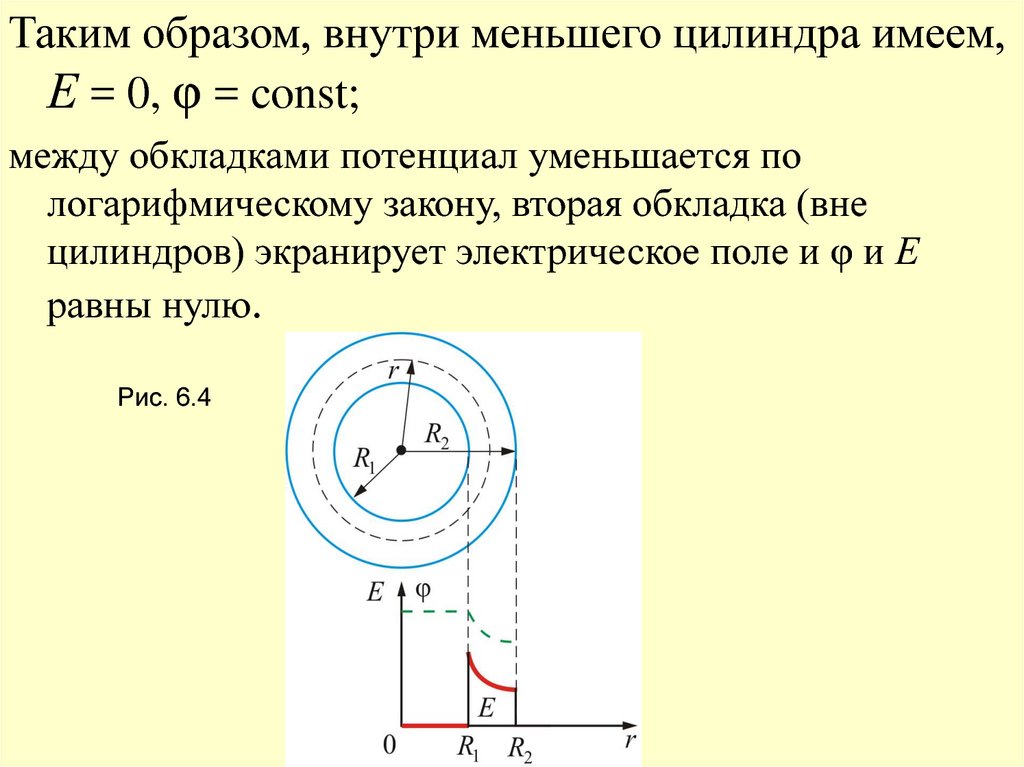
Таким образом, внутри меньшего цилиндра имеем,Е = 0, φ = const;
между обкладками потенциал уменьшается по
логарифмическому закону, вторая обкладка (вне
цилиндров) экранирует электрическое поле и φ и Е
равны нулю.
Рис. 6.4
20. 6. 3.4. Разность потенциалов между точками поля, образованного заряженной сферой (пустотелой)
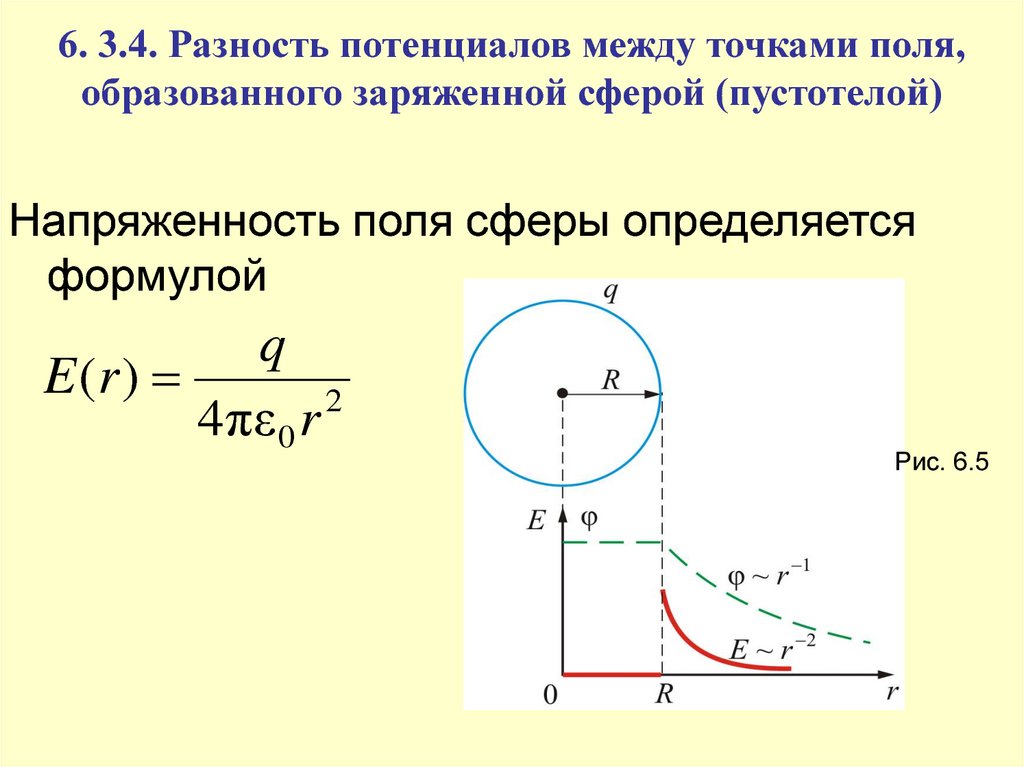
Напряженность поля сферы определяетсяформулой
q
E (r )
2
4 πε 0 r
Рис. 6.5
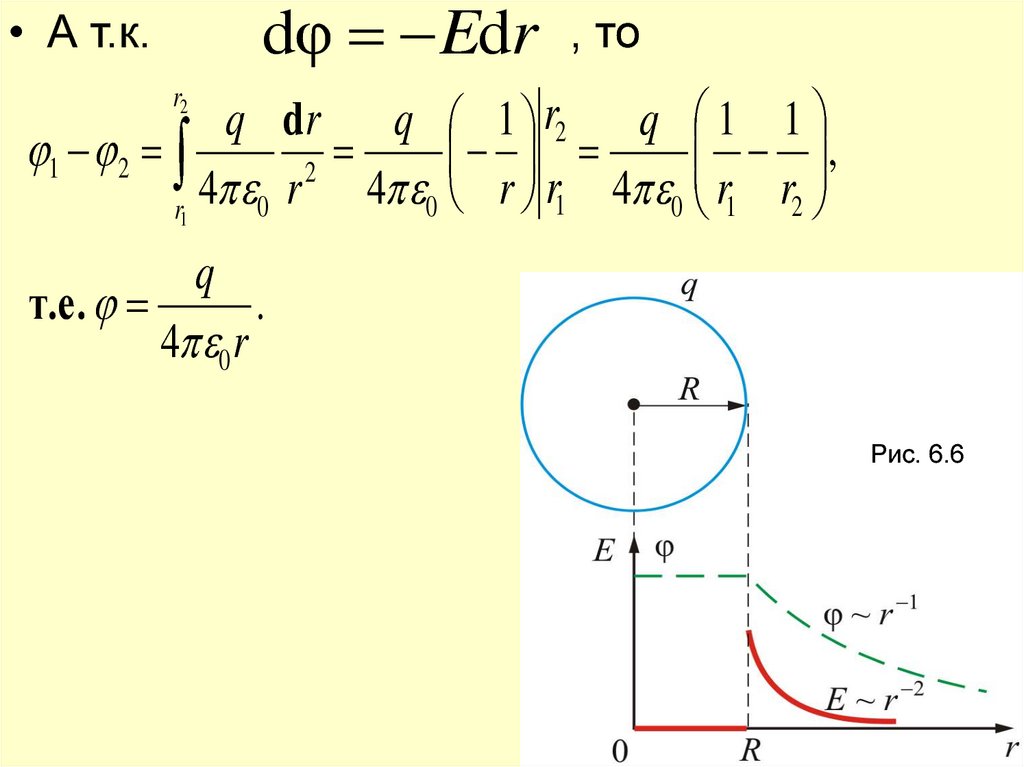
21.
dφ Edr• А т.к.
, то
q dr
q 1 r2 q 1 1
1 2
,
2
4 0 r 4 0 r r1 4 0 r1 r2
r1
r2
q
т.е.
.
4 0 r
Рис. 6.6
22.
• Из полученных соотношений можносделать следующие выводы:
• С помощью теоремы Гаусса
сравнительно просто можно
рассчитать Е и φ от различных
заряженных поверхностей.
• Напряженность поля в вакууме
изменяется скачком при переходе
через заряженную поверхность.
• Потенциал поля – всегда непрерывная
функция координат.
23.
Лекция 7Тема:
ДИЭЛЕКТРИКИ
В
ЭЛЕКТРОСТАТИЧЕСКОМ
ПОЛЕ
Сегодня: понедельник, 17 сентября 2018 г.
7.1. Поляризация диэлектриков;
7.2. Различные виды диэлектриков:
7.2.1. Сегнетоэлектрики;
7.2.2. Пьезоэлектрики;
7.2.3. Пироэлектрики;
7.3. Вектор электрического смещения D .
7.4. Поток вектора электрического смещения.
Теорема Гаусса для вектора D .
7.5. Изменение E и D на границе раздела
двух диэлектриков.
24.
До сих пор мы рассматривалиэлектростатические
поля
и
взаимодействие зарядов в вакууме. Как
ведут себя заряды в среде? Что
происходит
с
веществом
в
электростатическом поле?
25.
Электрический диполь.р = ql - электрический дипольный момент.
2q1r1 sin
p
E 2 E1 sin
3
3
4 0 r
4 0 r1
E
p
4 0 r
3
25
26.
Диполь во внешнем полеF qE и F- qE
M qE l sin pE sin
M pE
Электрическое поле стремится повернуть ось диполя так, чтобы его
электрический момент р установился по направлению поля. Положение
равновесия, когда векторы p и E параллельны, устойчиво.
Энергия диполя во
W q q q
внешнем поле
l E l
W pE
l;
El l
l
2
6
27. 4.1. Поляризация диэлектриков
• Все известные в природе вещества, всоответствии с их способностью проводить
электрический ток, делятся на
три основных класса:
• диэлектрики
• полупроводники
• проводники
ρд ρп/п ρпр .
6
8
ρ пр 10 10 Ом/м
28.
• В идеальном диэлектрикесвободных зарядов, то есть
способных перемещаться на
значительные расстояния
(превосходящие расстояния между
атомами), нет.
• Но это не значит, что диэлектрик,
помещенный в электростатическое
поле, не реагирует на него, что в нем
ничего не происходит.
29.
• Смещение электрическихзарядов вещества под
действием электрического поля
называется поляризацией.
• Способность к поляризации
является основным свойством
диэлектриков.
30.
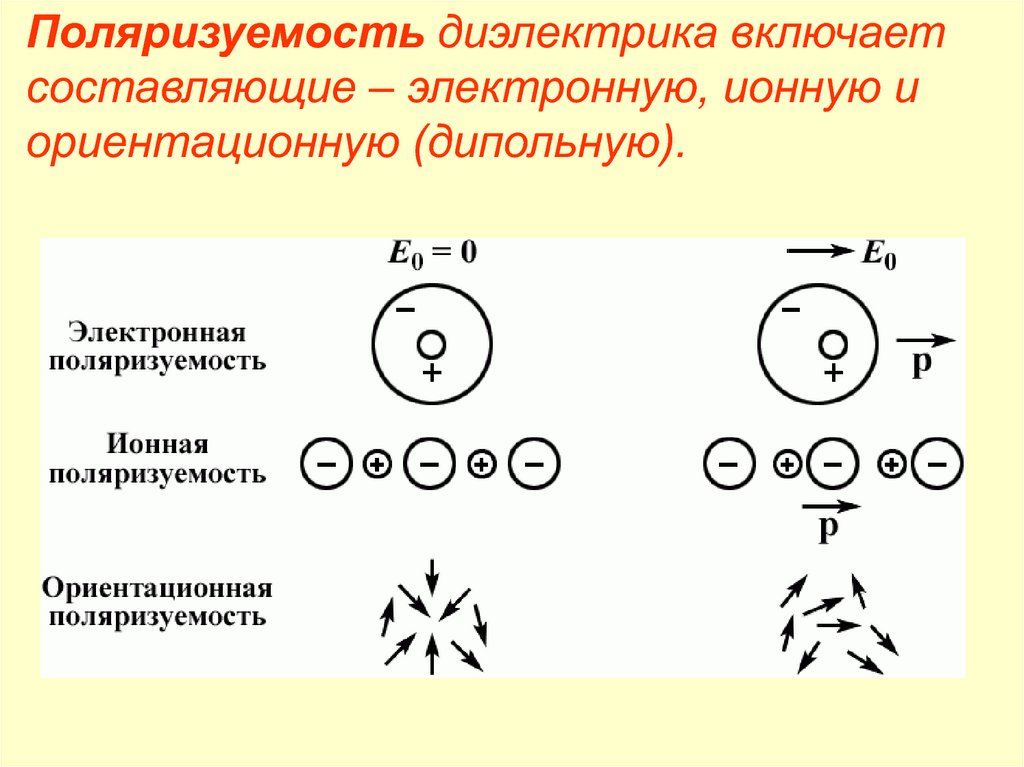
Поляризуемость диэлектрика включаетсоставляющие – электронную, ионную и
ориентационную (дипольную).
31.
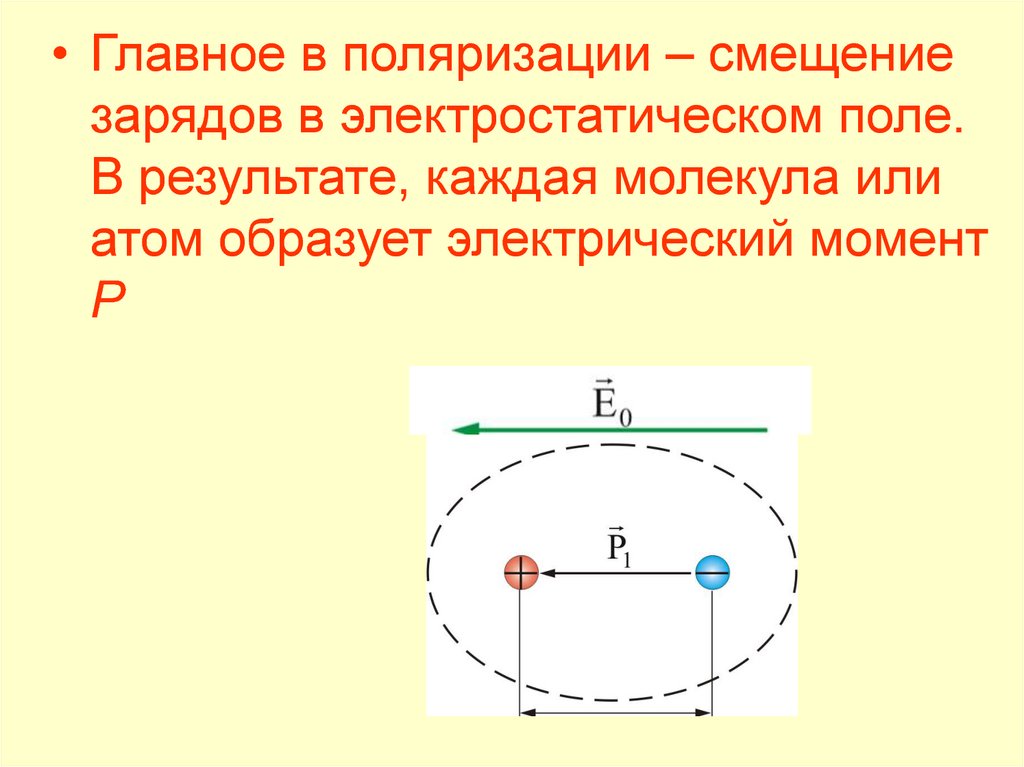
• Главное в поляризации – смещениезарядов в электростатическом поле.
В результате, каждая молекула или
атом образует электрический момент
Р
32.
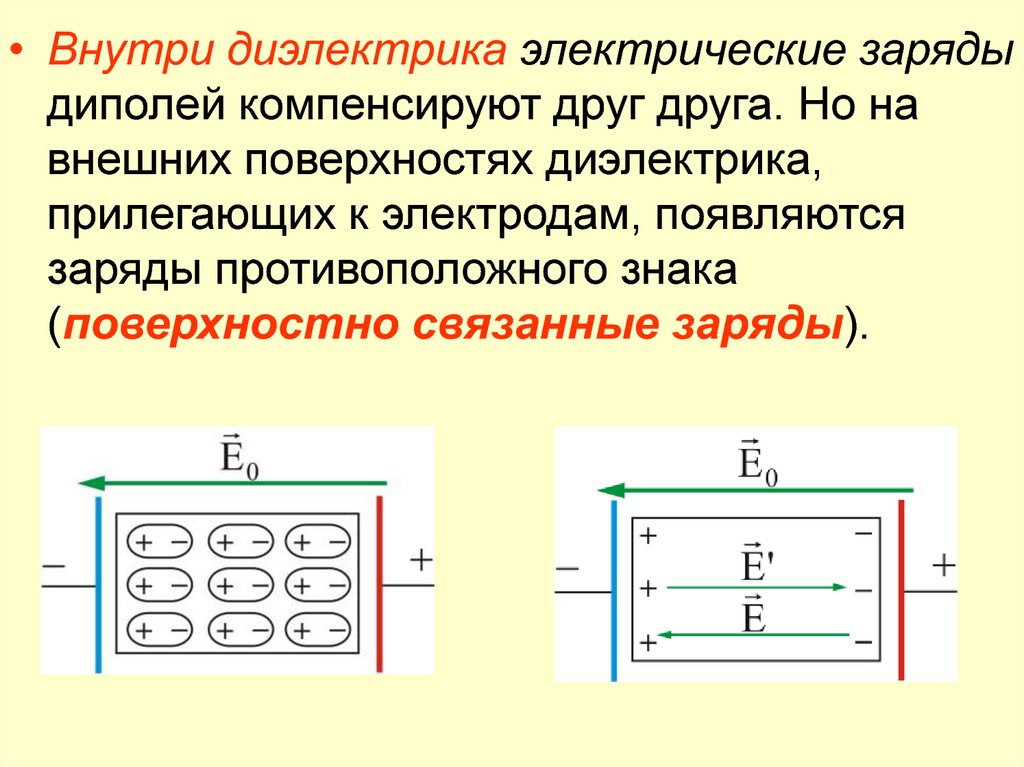
• Внутри диэлектрика электрические зарядыдиполей компенсируют друг друга. Но на
внешних поверхностях диэлектрика,
прилегающих к электродам, появляются
заряды противоположного знака
(поверхностно связанные заряды).
33.
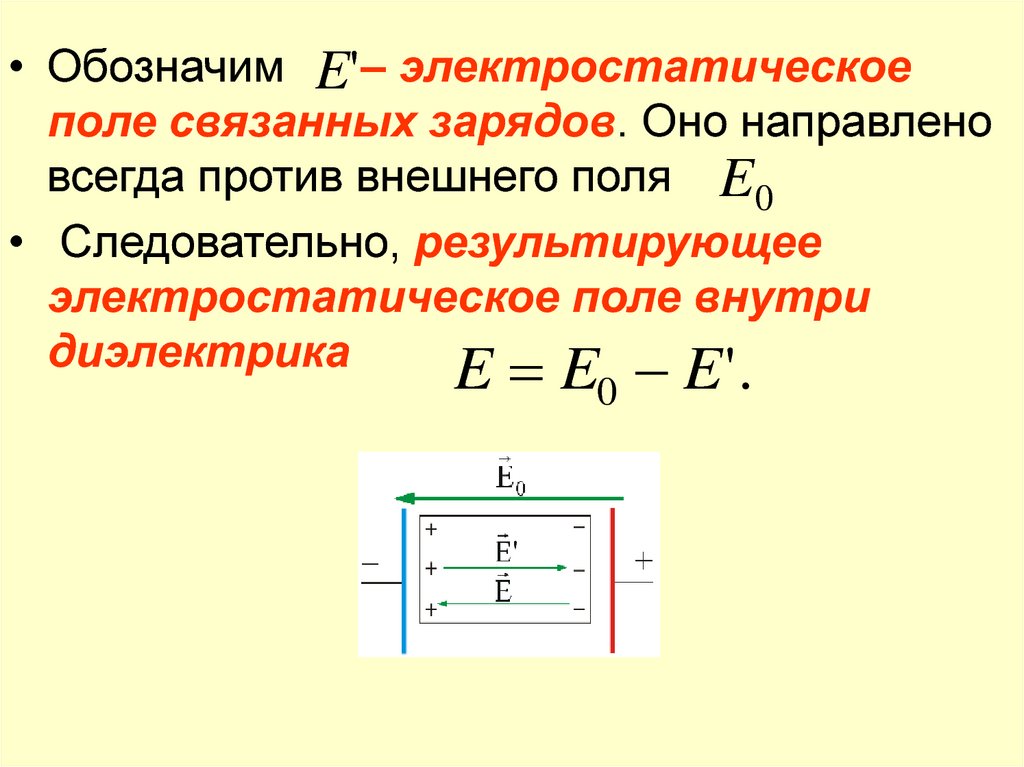
• Обозначим E'– электростатическоеполе связанных зарядов. Оно направлено
всегда против внешнего поля E 0
• Следовательно, результирующее
электростатическое поле внутри
диэлектрика
E E E '.
0
34.
• Поместим диэлектрик в видепараллелепипеда в
электростатическое поле E
0
• Электрический момент тела, можно найти по формуле:
– поверхностная плотность связанных зарядов.
σ'
P q l σ' S l , или P σ' Slcosφ,
35.
• Введем новое понятие – векторполяризации – электрический
момент единичного объема.
n
(4.1.4)
P P1k nP1 ,
k
• где n – концентрация молекул в единице
объема,
• P – электрический момент одной
1
молекулы.
36.
• С учетом этого обстоятельства,P PV PSl cos φ (4.1.5)
• (т.к.
V Sl cosφ – объем
параллелепипеда).
• Приравняем (4.1.3.) и (4.1.5) и
учтем, что
– проекция P на направление n –
вектора нормали,
• тогда
P cos φ Pn
σ' P n
37.
σ' P n• Поверхностная плотность
поляризационных зарядов равна
нормальной составляющей вектора
поляризации в данной точке поверхности.
• Отсюда следует, что индуцированное в
диэлектрике электростатическое поле
E' будет влиять только на нормальную
составляющую вектора напряженности
электростатического поля E .
38.
• Вектор поляризации можно представитьтак:
• P nP nαε E χε E, (4.1.7)
1
α
0
0
• где
– поляризуемость молекул,
χ nα – диэлектрическая
восприимчивость – макроскопическая
безразмерная величина, характеризующая
поляризацию единицы объема.
39.
Следовательно, и у результирующегополя E
изменяется, по сравнению с E 0 ,только
нормальная составляющая.
Тангенциальная составляющая поля
остается без изменения.
В векторной форме результирующее поле
можно представить
так:
(4.1.8)
E E0 E'.
Результирующая электростатического
поля в диэлектрике равно внешнему полю,
деленному на диэлектрическую
E0
проницаемость среды ε:
E
.
ε (4.1.9)
40.
• Величина ε 1 χ характеризуетэлектрические свойства диэлектрика.
• Физический смысл диэлектрической
проницаемости среды ε – величина,
показывающая во сколько раз
электростатическое поле внутри
диэлектрика меньше, чем в вакууме:
E0
(4.1.10)
ε
E
.
41.
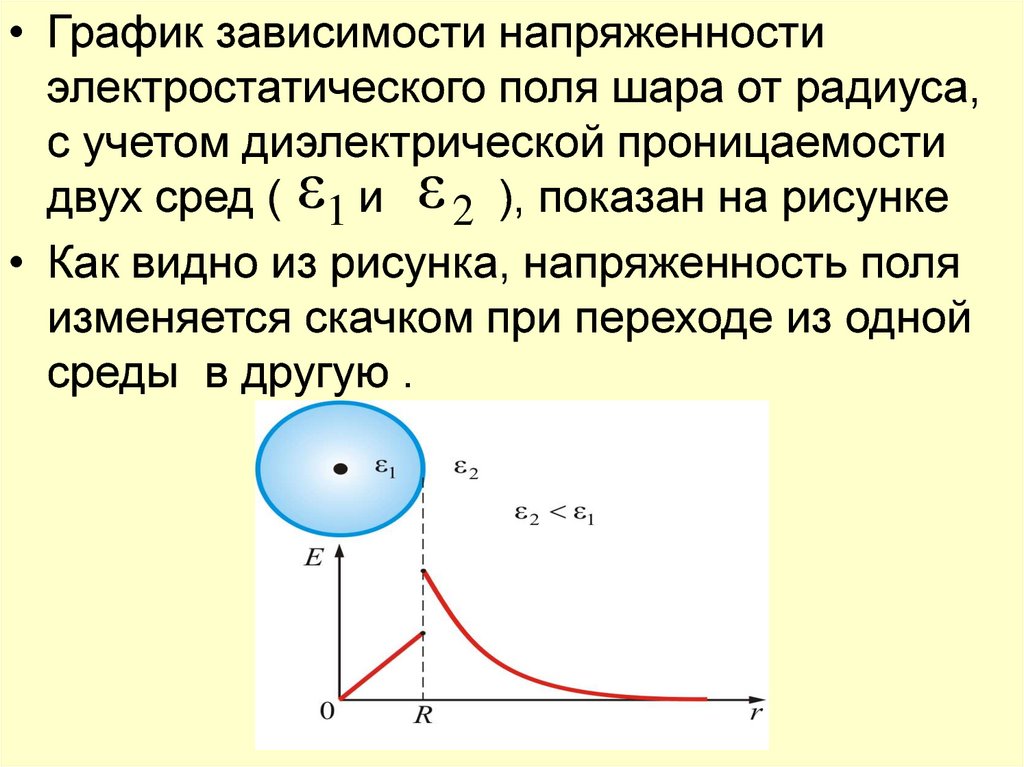
• График зависимости напряженностиэлектростатического поля шара от радиуса,
с учетом диэлектрической проницаемости
двух сред ( ε1 и ε 2 ), показан на рисунке
• Как видно из рисунка, напряженность поля
изменяется скачком при переходе из одной
среды в другую .
42. 4.2. Различные виды диэлектриков
• В 1920 г. была открыта спонтанная(самопроизвольная) поляризация.
• Всю группу веществ, назвали
сегнетоэлектрики (или ферроэлектрики).
• Все сегнетоэлектрики обнаруживают резкую
анизотропию свойств (сегнетоэлектрические
свойства могут наблюдаться только вдоль
одной из осей кристалла). У изотропных
диэлектриков поляризация всех молекул
одинакова, у анизотропных – поляризация, и
следовательно, вектор поляризации в
разных направлениях разные.
43.
• Рассмотрим основные свойствасегнетоэлектриков:
• 1. Диэлектрическая проницаемость ε в
некотором температурном интервале
велика( ε ~ 103 10 4 ).
• 2. Значение ε зависит не только от внешнего
поля E0, но и от предыстории образца.
• 3. Диэлектрическая проницаемость ε (а
следовательно, и Р ) – нелинейно зависит от
напряженности внешнего
электростатического поля (нелинейные
диэлектрики).
44.
• Это свойство называется диэлектрическимгистерезисом
• Здесь точка а – состояние насыщения.
45.
• 4. Наличие точки Кюри – температуры,при которой (и выше)
сегнетоэлектрические свойства
пропадают. При этой температуре
происходит фазовый переход 2-го рода.
Например,
• титанат бария: 133º С;
• сегнетова соль: – 18 + 24º С;
• ниобат лития 1210º С.
46.
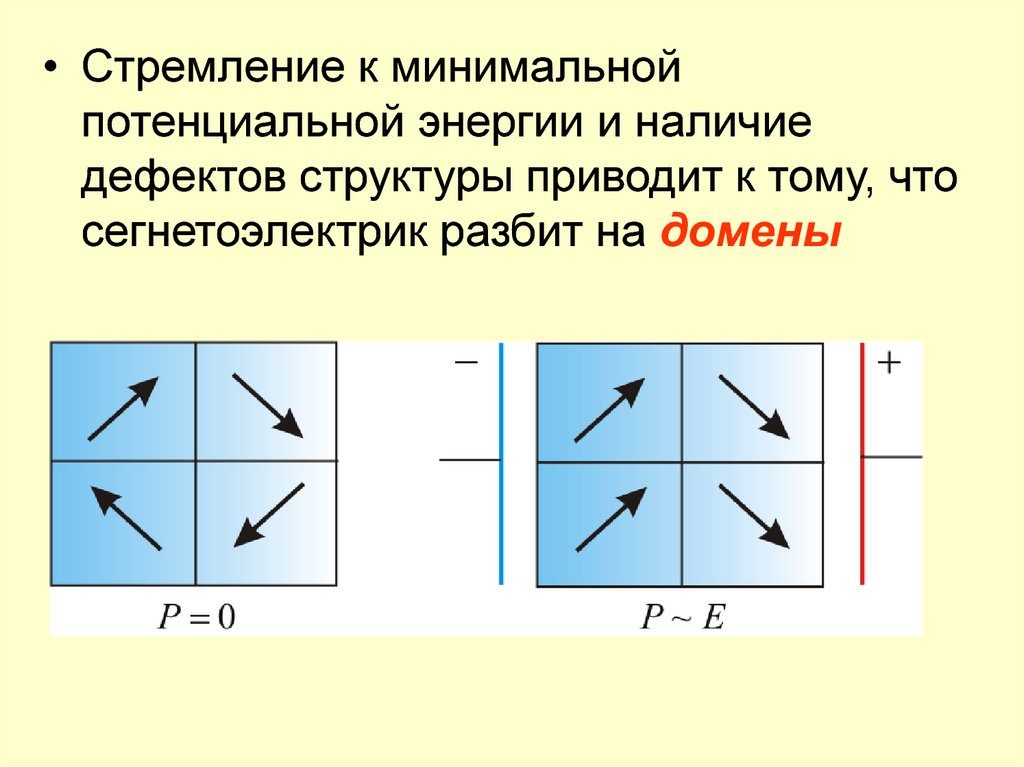
• Стремление к минимальнойпотенциальной энергии и наличие
дефектов структуры приводит к тому, что
сегнетоэлектрик разбит на домены
47.
• Среди диэлектриков естьвещества, называемые
электреты – диэлектрики,
длительно сохраняющие
поляризованное состояние после
снятия внешнего
электростатического поля
(аналоги постоянных магнитов).
48. Пьезоэлектрики
Некоторые диэлектрики поляризуютсяне только под действием электрического
поля, но и под действием механической
деформации. Это явление называется
пьезоэлектрическим эффектом.
• Явление открыто братьями Пьером и
Жаком Кюри в 1880 году.
• Если на грани кристалла наложить
металлические электроды (обкладки) то
при деформации кристалла на обкладках
возникнет разность потенциалов.
• Если замкнуть обкладки, то потечет
ток.
49.
Рис. 4.7Возможен и обратный пьезоэлектрический эффект:
• Возникновение поляризации сопровождается
механическими деформациями.
• Если на пьезоэлектрический кристалл подать
напряжение, то возникнут механические деформации
кристалла, причем, деформации будут пропорциональны
приложенному электрическому полю Е .
50.
•Сейчас известно более 1800пьезокристаллов.
•Все сегнетоэлектрики обладают
пьезоэлектрическими свойствами
• Используются в пьезоэлектрических
адаптерах и других устройствах).
51. 4.2.3. Пироэлектрики
Пироэлектричество – появлениеэлектрических зарядов на поверхности
некоторых кристаллов при их
нагревании или охлаждении.
• При нагревании один конец
диэлектрика заряжается положительно, а
при охлаждении он же – отрицательно.
• Появление зарядов связано с
изменением существующей поляризации
при изменении температуры кристаллов.
52.
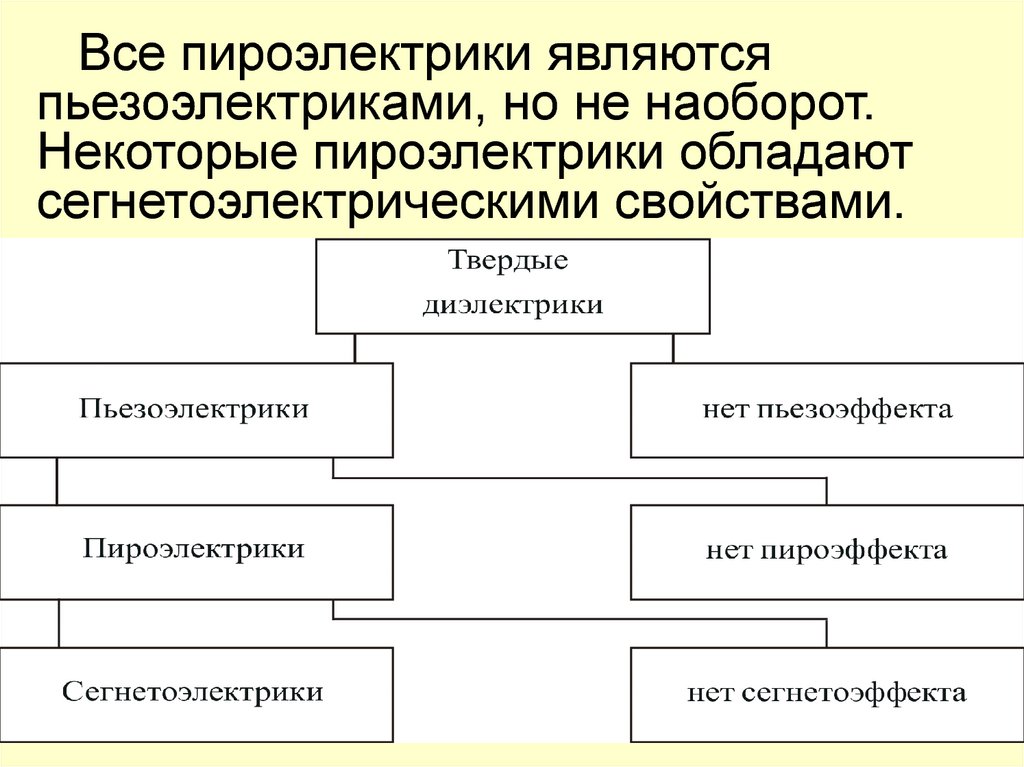
Все пироэлектрики являютсяпьезоэлектриками, но не наоборот.
Некоторые пироэлектрики обладают
сегнетоэлектрическими свойствами.
53.
В качестве примеров использованияразличных диэлектриков можно привести:
сегнетоэлектрики – электрические
конденсаторы, ограничители предельно
допустимого тока, позисторы, запоминающие
устройства;
пьезоэлектрики – генераторы ВЧ и
пошаговые моторы, микрофоны, наушники,
датчики давления, частотные фильтры,
пьезоэлектрические адаптеры;
пироэлектрики – позисторы, детекторы ИКизлучения, болометры (датчики
инфракрасного излучения),
электрооптические модуляторы.
54. 4.3. Вектор электрического смещения
DИмеем границу раздела двух сред с ε1 и ε2,
так что, ε1 < ε2 (рис. 4.8).
E1 ε2
E2 ε1
или
ε2
E1 E2
ε1
Напряженность
электрического поля E
изменяется скачком при
переходе из одной среды в
другую.
Рис. 4.8
55.
• Главная задача электростатики –расчет электрических полей, то есть E
в различных электрических аппаратах,
кабелях, конденсаторах,….
• Эти расчеты сами по себе не просты
да еще наличие разного сорта
диэлектриков и проводников еще
более усложняют задачу.
56.
• Для упрощения расчетов была введенановая векторная величина – вектор
электрического смещения
(электрическая индукция).
D ε0 εE
(4.3.1)
• Из предыдущих рассуждений E1ε1 = ε2E2
тогда ε0ε1E1 = ε0ε2E2 отсюда и
Dn1 = Dn2.
57.
Dn1 = Dn2.Таким образом, вектор D
остается неизменным
при переходе из одной
среды в другую и это
облегчает расчет D .
58.
ЗнаяD и ε, легко рассчитывать
D
E
.
ε 0ε
59.
D εε 0 E (1 χ )ε 0 E ε 0 E χε 0 Eотсюда можно записать:
где
χ
P
D ε 0E P,
–
(4.3.3)
вектор поляризации,
– диэлектрическая восприимчивость
среды, характеризующая поляризацию
единичного объема среды.
60.
• Для точечного заряда в вакуумеD
q
D
.
2
4πr
• Для
имеет место принцип
суперпозиции, как и для E , т.е.
n
D Dk .
k 1
61. 4.4. Поток вектора электрического смещения. Теорема Остроградского-Гаусса для вектора
DПусть произвольную площадку S пересекают
линии
вектора электрического смещения D под углом α
к нормали:
62.
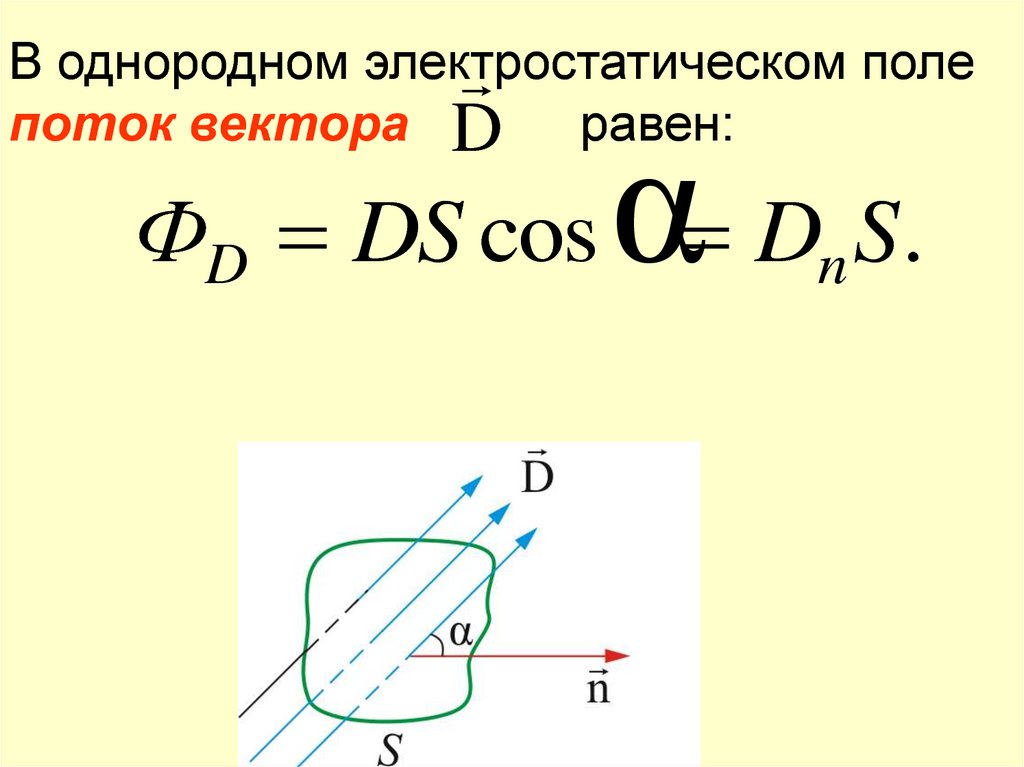
В однородном электростатическомполе
поток вектора D
равен:
ФD DS cos α Dn S .
63.
Теорему Остроградского-Гаусса длявектора D получим из теоремы
Остроградского-Гаусса для вектора E :
ФE
S
qk
E dS
n
ε 0ε
qk
1
Dn dS
ε 0ε s
ε 0ε
Dn
En
ε 0ε
64.
D• Теорема Остроградского-Гаусса для
(4.4.1)
ФD
Dn dS
S
qk .
D
• Поток вектора
через любую замкнутую
поверхность определяется только
свободными зарядами, а не всеми
зарядами внутри объема, ограниченного
данной поверхностью.
• Это позволяет не рассматривать связанные
(поляризованные) заряды, влияющие на E и
упрощает решение многих задач.
• В этом смысл введения вектора
D
.
65. 4.5. Изменение и на границе раздела двух диэлектриков
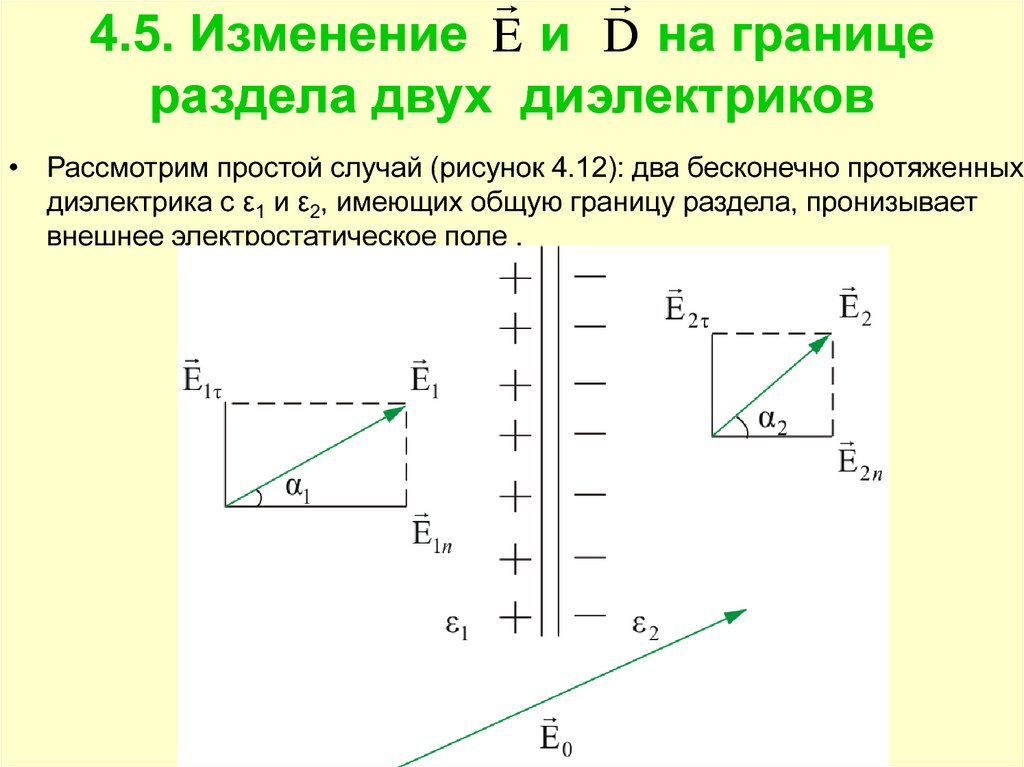
4.5. Изменение E и D на границераздела двух диэлектриков
• Рассмотрим простой случай (рисунок 4.12): два бесконечно протяженных
диэлектрика с ε1 и ε2, имеющих общую границу раздела, пронизывает
внешнее электростатическое поле .
66.
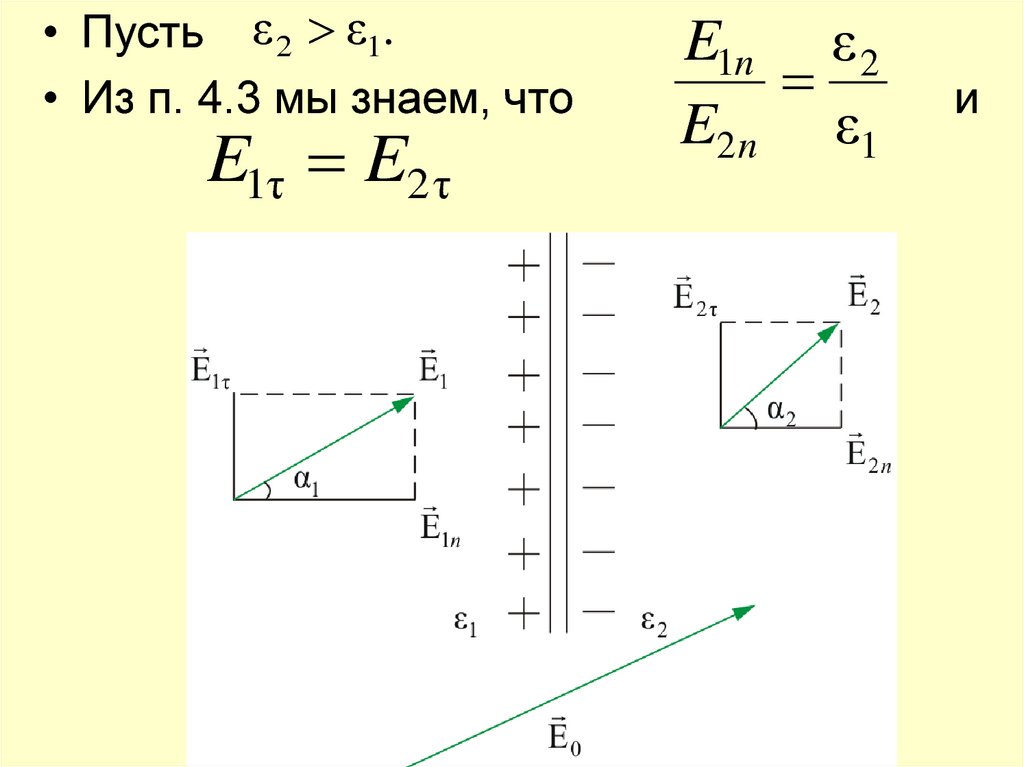
• Пусть ε 2 ε1.• Из п. 4.3 мы знаем, что
E1τ E2 τ
E1n ε 2
E2 n ε1
и
67.
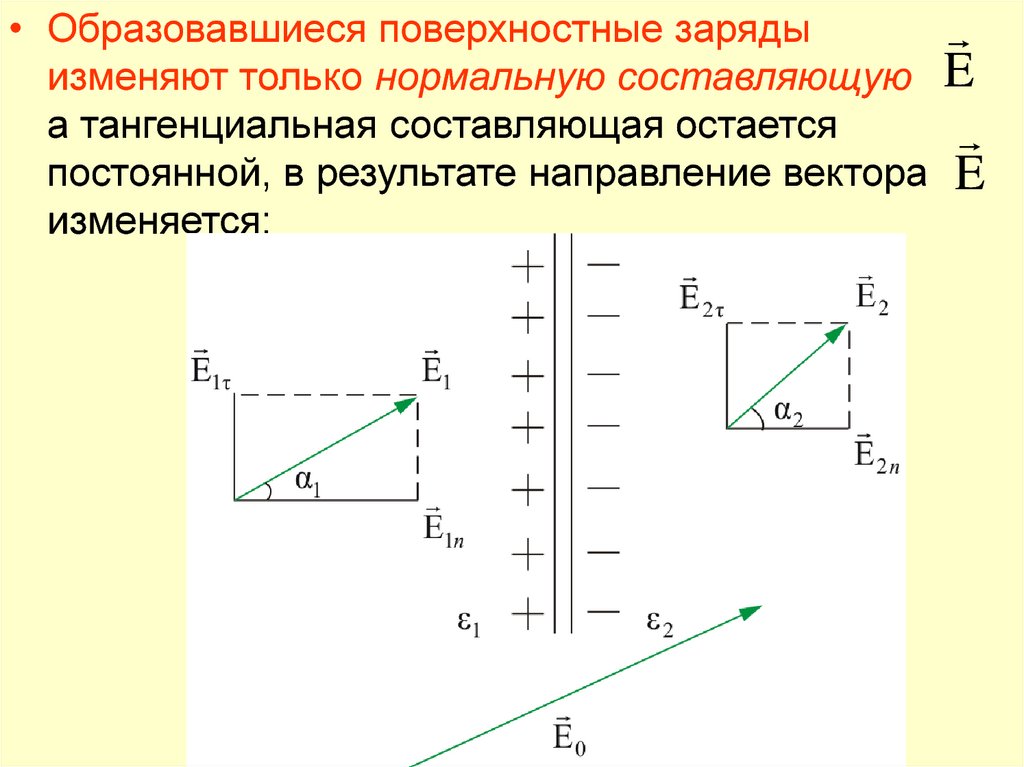
• Образовавшиеся поверхностные зарядыизменяют только нормальную составляющую
а тангенциальная составляющая остается
постоянной, в результате направление вектора
изменяется:
E
E
68.
• То есть направление вектора Eизменяется: tg α
E E
E
1
tg α 2
2 τ 1n
E2 n E1τ
1n
E2 n
ε2
,
ε1
tg α1 ε 2
,
tg α 2 ε1
• Это закон преломления вектора
напряженности
электростатического поля.
69.
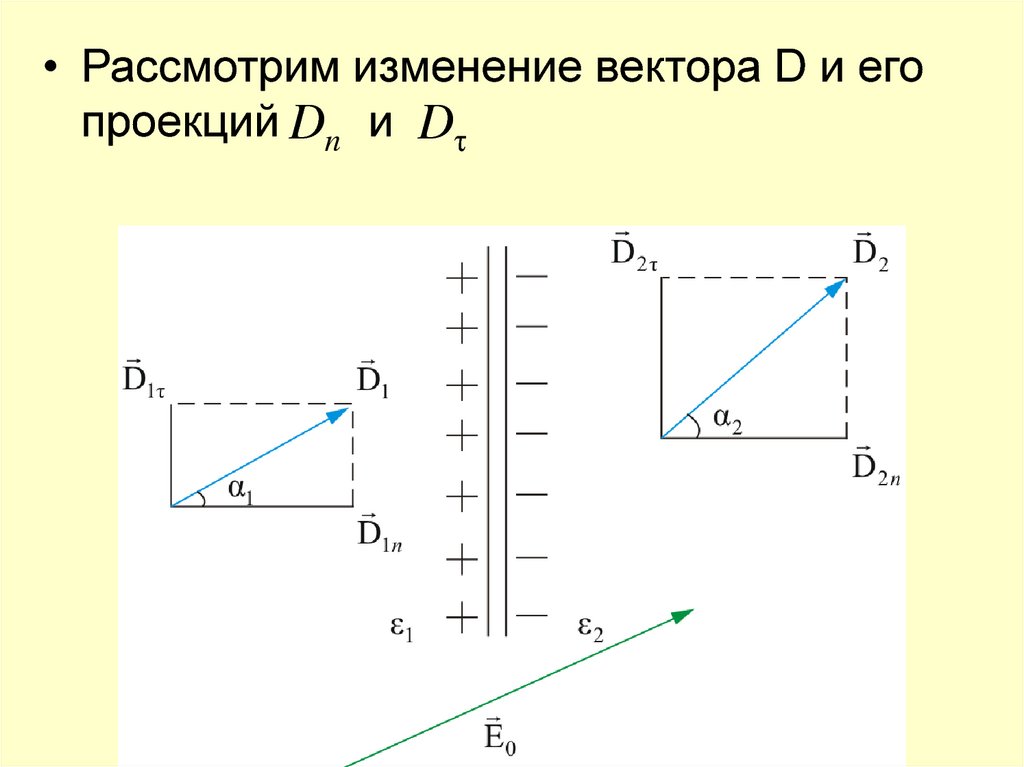
• Рассмотрим изменение вектора D и егопроекций Dn и Dτ
70.
• Т.к. D ε 0 εE , то имеем:D1n ε1ε 0 E1n
D2 n ε 2ε 0 E2 n
D1n
ε1ε 0 E1n
ε 0 ε1ε 2
1
D2 n
ε 2 ε 0 E2 n
ε 0 ε 2 ε1
• т.е. D1n D2 n – нормальная составляющая
вектора не изменяется.
D1τ
ε1ε 0 E1τ
ε1
;
D2 τ
ε 2 ε 0 E2 τ
ε2
D2 τ D1τ
ε2
ε1
• т.е. тангенциальная составляющая вектора
увеличивается в ε 2 раз
ε
71.
tg α1 D2 τ D1n D2 τ ε 2tg α 2 D2n D1τ D1τ ε1
tg α1 ε 2
tg α 2 ε1
• закон преломления вектора D .
72.
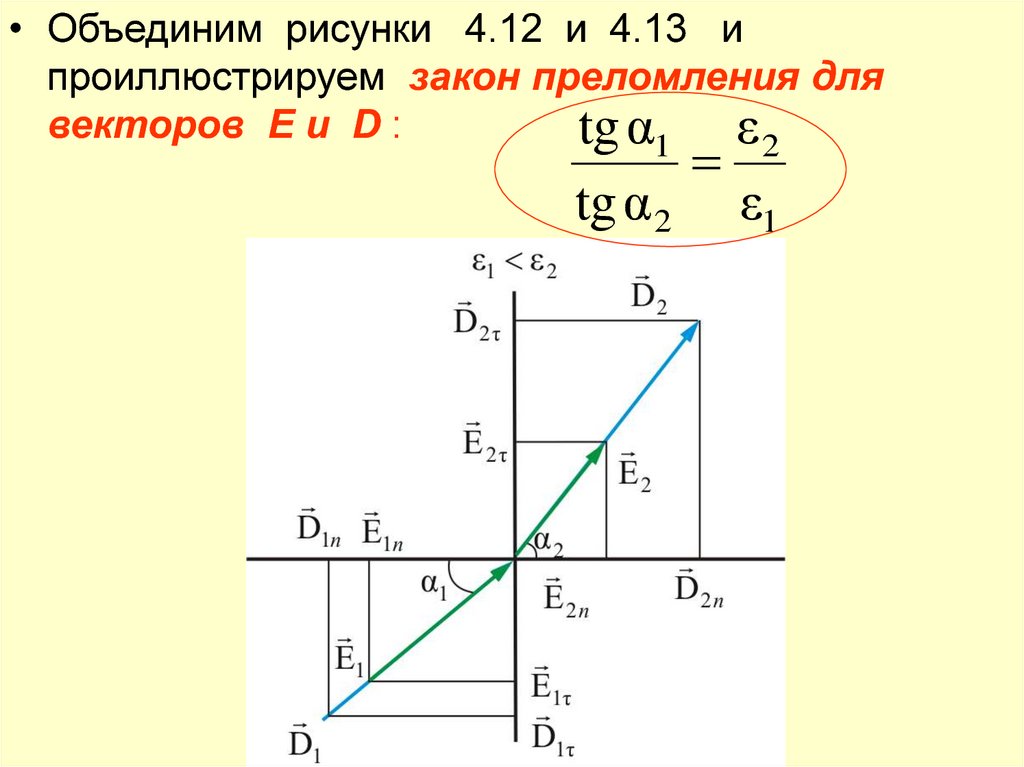
• Объединим рисунки 4.12 и 4.13 ипроиллюстрируем закон преломления для
векторов E и D :
tg α1 ε 2
tg α 2
ε1
73.
• Как видно из рисунка, при переходе из однойдиэлектрической среды
в другую вектор D – преломляется
на тот же угол, что и E
D εε 0 E
• Входя в диэлектрик с большей
диэлектрической
проницаемостью, линии D и E удаляются от нормали.
74.
Сегодня: понедельник, 17 сентября 2018 г.Лекция окончена.
До свидания!
УРА! УРА! УРА!
75.
Сегодня: понедельник, 17 сентября 2018г.
Лекция окончена.
До свидания!












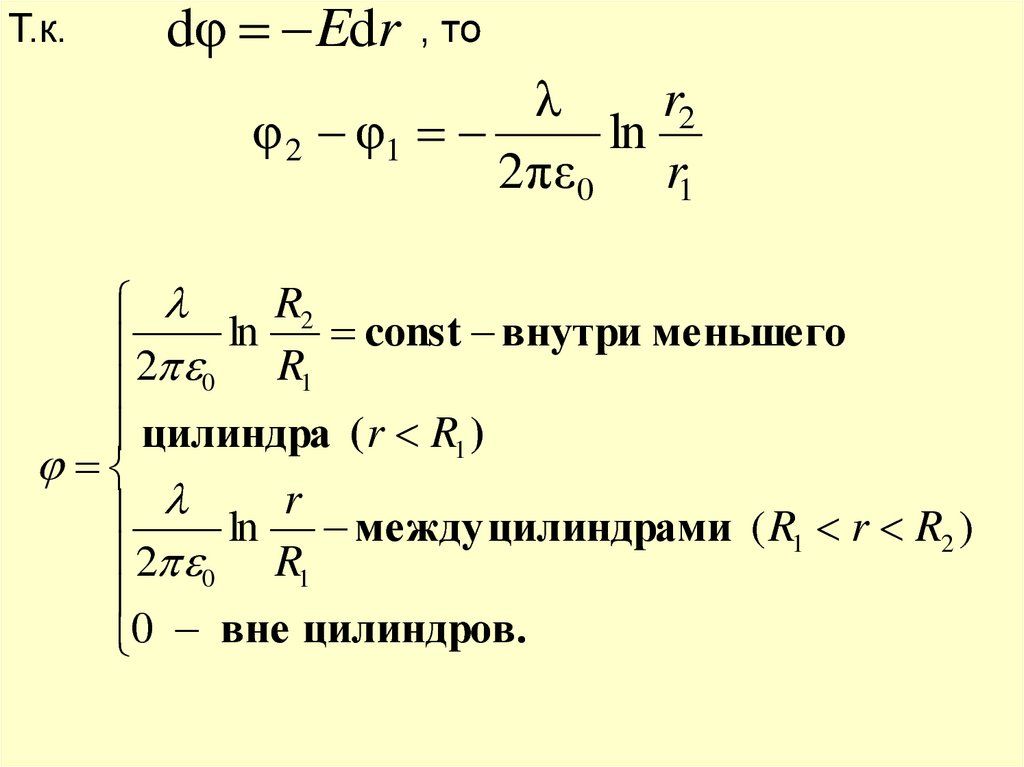









































 Физика
Физика








