Похожие презентации:
Графическое решение задачи линейного программирования с двумя переменными
1. Графическое решение задачи линейного программирования в случае двух переменных
2.
Решим графически задачу:Максимизировать
функцию:
при ограничениях:
f ( x) 3 x1 2 x2
2 x1 4 x2 100
x 40
1
x2 20
x1 0, x2 0
3.
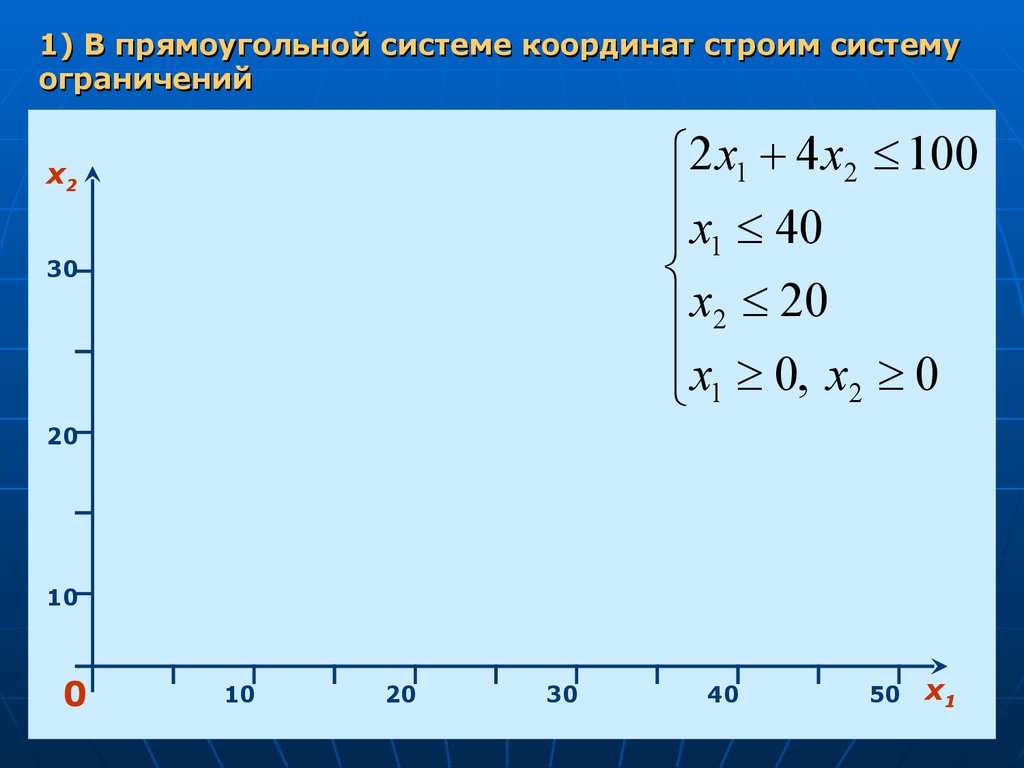
1) В прямоугольной системе координат строим системуограничений
2 x1 4 x2 100
x 40
1
x2 20
x1 0, x2 0
х2
30
20
10
0
10
20
30
40
50
х1
4.
1) В прямоугольной системе координат строим системуограничений
Полуплоскость
х2
х1
30
2 x1 4 x2 100
х2
0
25
50
0
20
2 x1 4 x2 100
10
0
10
20
30
40
50
х1
5.
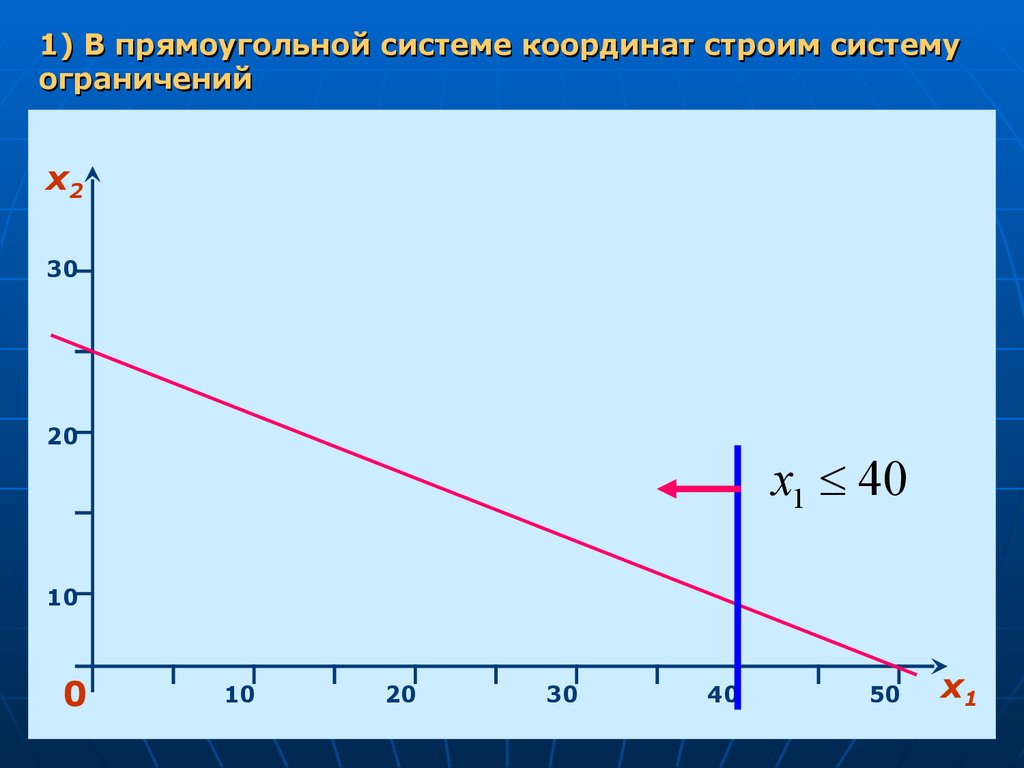
1) В прямоугольной системе координат строим системуограничений
х2
30
20
x1 40
10
0
10
20
30
40
50
х1
6.
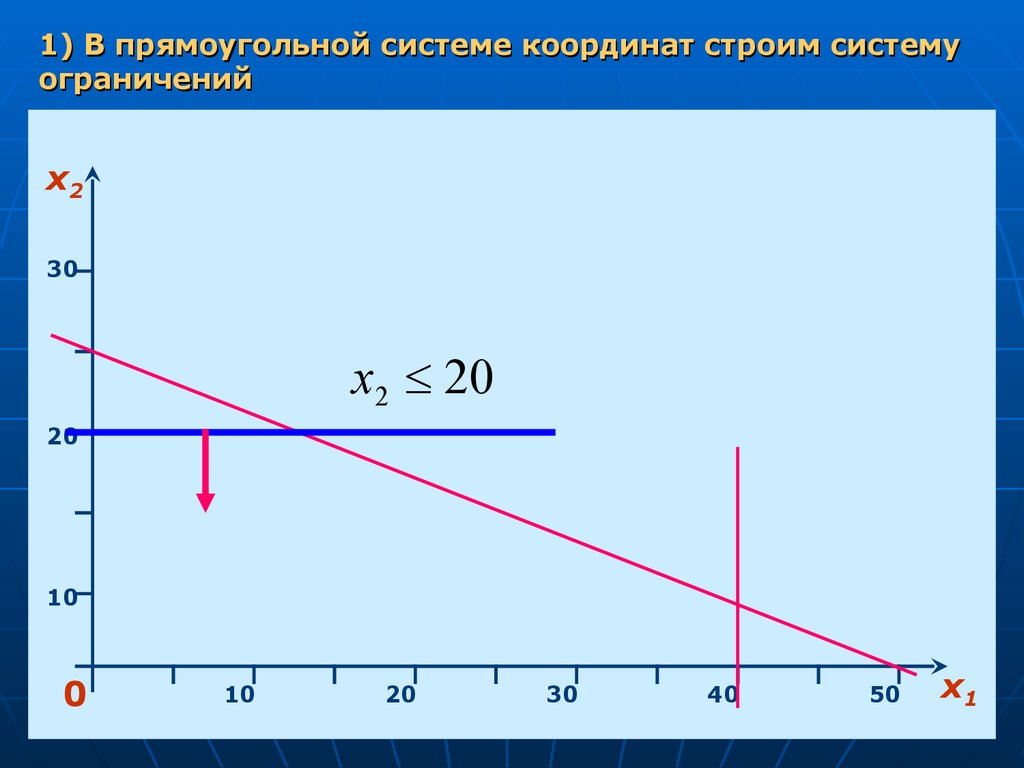
1) В прямоугольной системе координат строим системуограничений
х2
30
x2 20
20
10
0
10
20
30
40
50
х1
7.
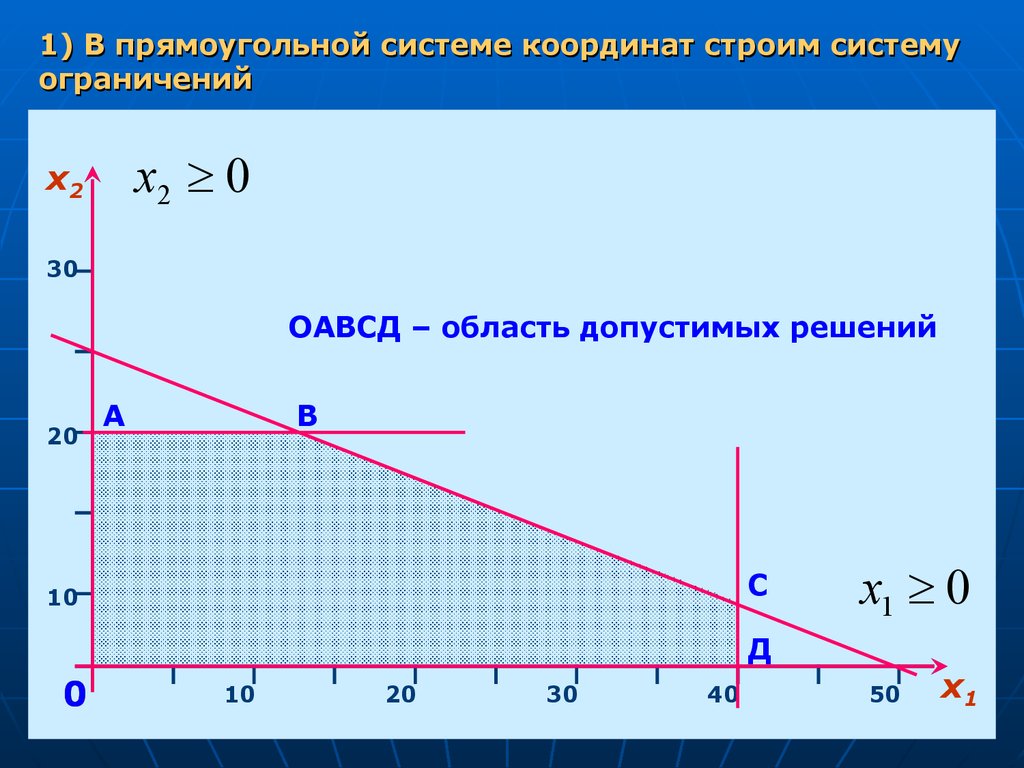
1) В прямоугольной системе координат строим системуограничений
x2 0
х2
30
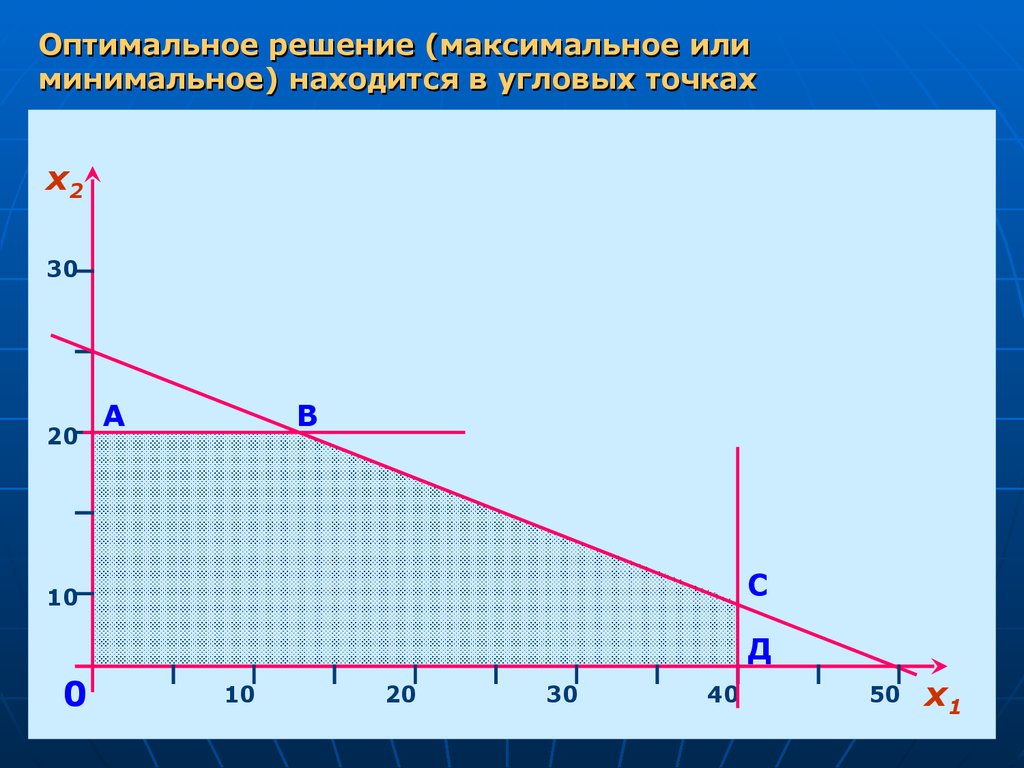
ОАВСД – область допустимых решений
20
А
В
С
10
x1 0
Д
0
10
20
30
40
50
х1
8.
Оптимальное решение (максимальное илиминимальное) находится в угловых точках
х2
30
20
А
В
С
10
Д
0
10
20
30
40
50
х1
9.
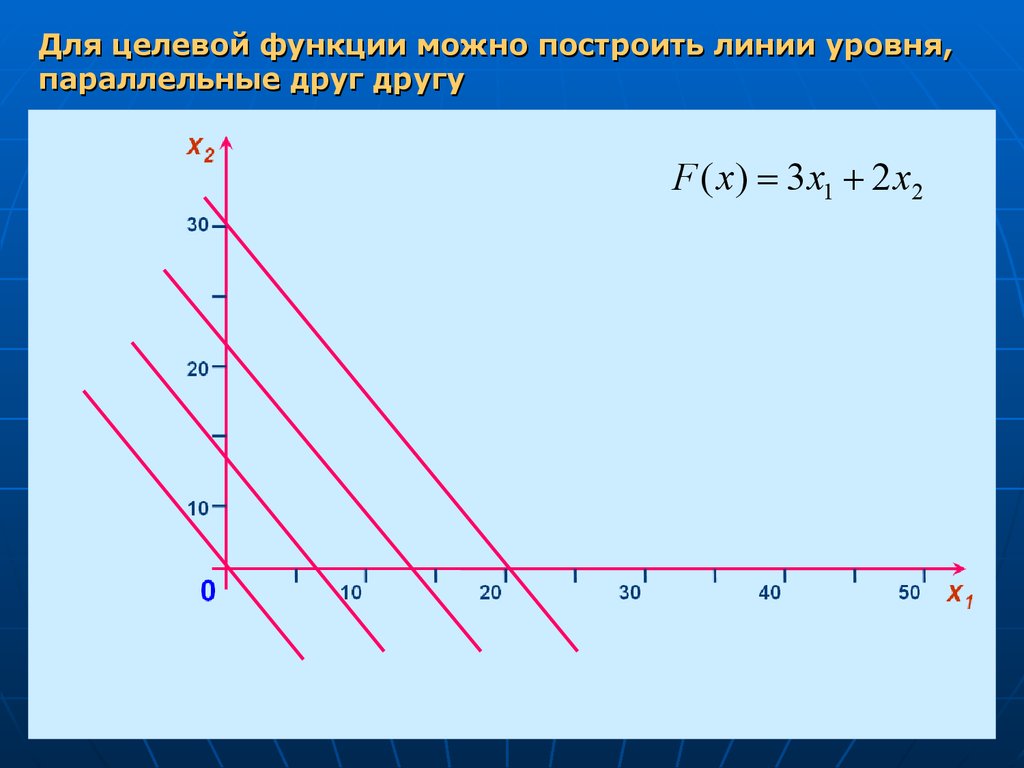
Для целевой функции можно построить линии уровня,параллельные друг другу
F ( x) 3 x1 2 x2
10.
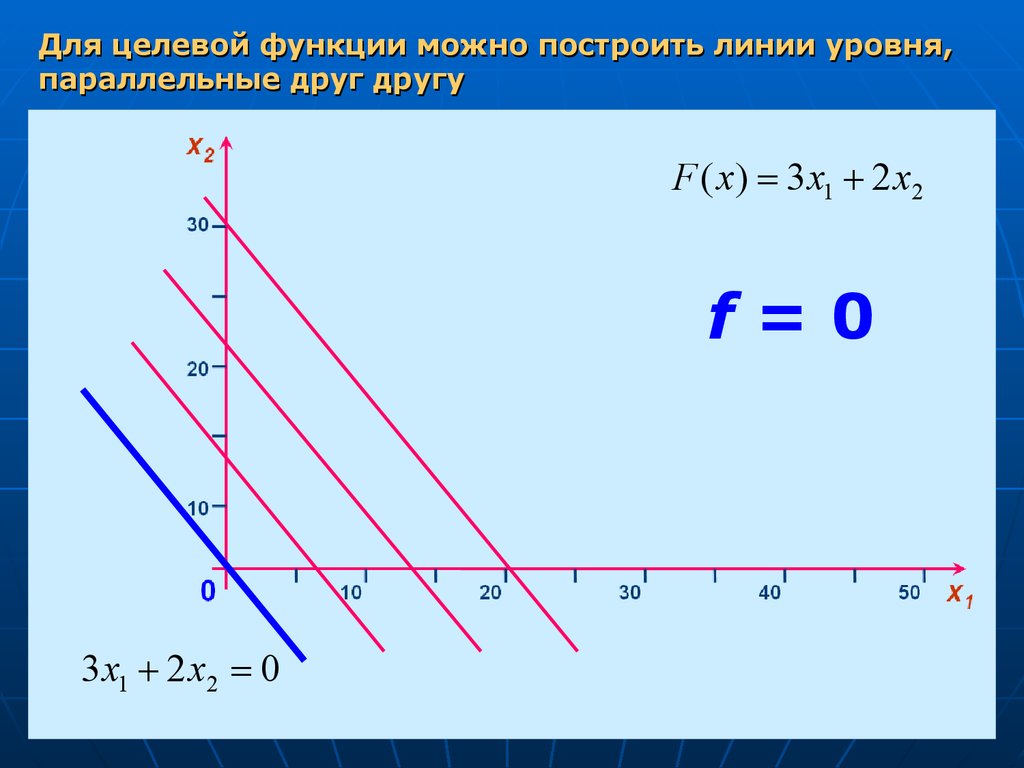
Для целевой функции можно построить линии уровня,параллельные друг другу
F ( x) 3 x1 2 x2
f=0
3 x1 2 x2 0
11.
Для целевой функции можно построить линии уровня,параллельные друг другу
F ( x) 3 x1 2 x2
f = 28
3 x1 2 x2 28
12.
Для целевой функции можно построить линии уровня,параллельные друг другу
F ( x) 3 x1 2 x2
f = 44
3 x1 2 x2 44
13.
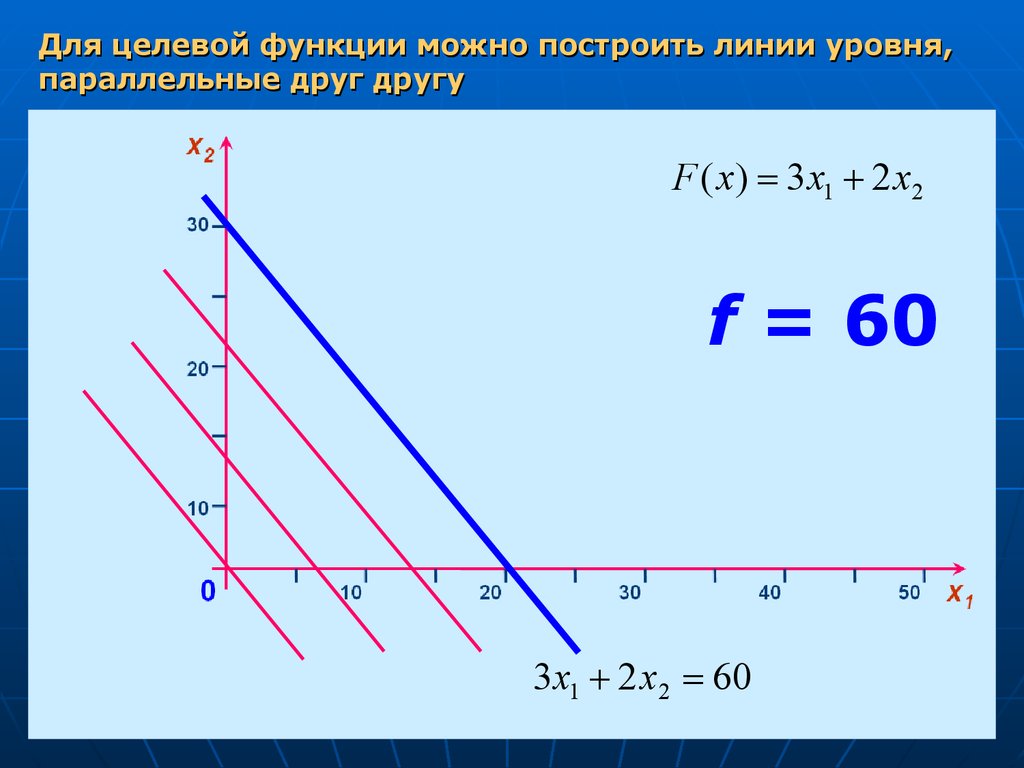
Для целевой функции можно построить линии уровня,параллельные друг другу
F ( x) 3 x1 2 x2
f = 60
3 x1 2 x2 60
14.
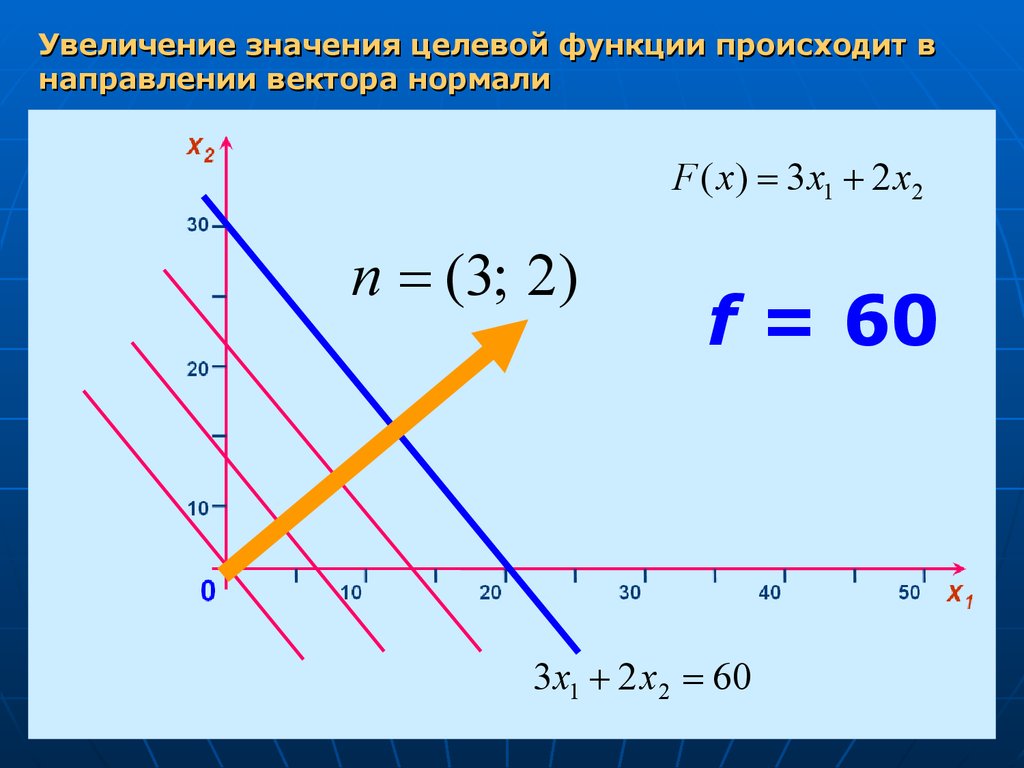
Увеличение значения целевой функции происходит внаправлении вектора нормали
F ( x) 3 x1 2 x2
n (3; 2)
f = 60
3 x1 2 x2 60
15.
Опорную прямую двигаем в направлении векторанормали
х2
30
20
А
3 x1 2 x2 0
В
С
10
Д
0
10
20
30
40
50
х1
16.
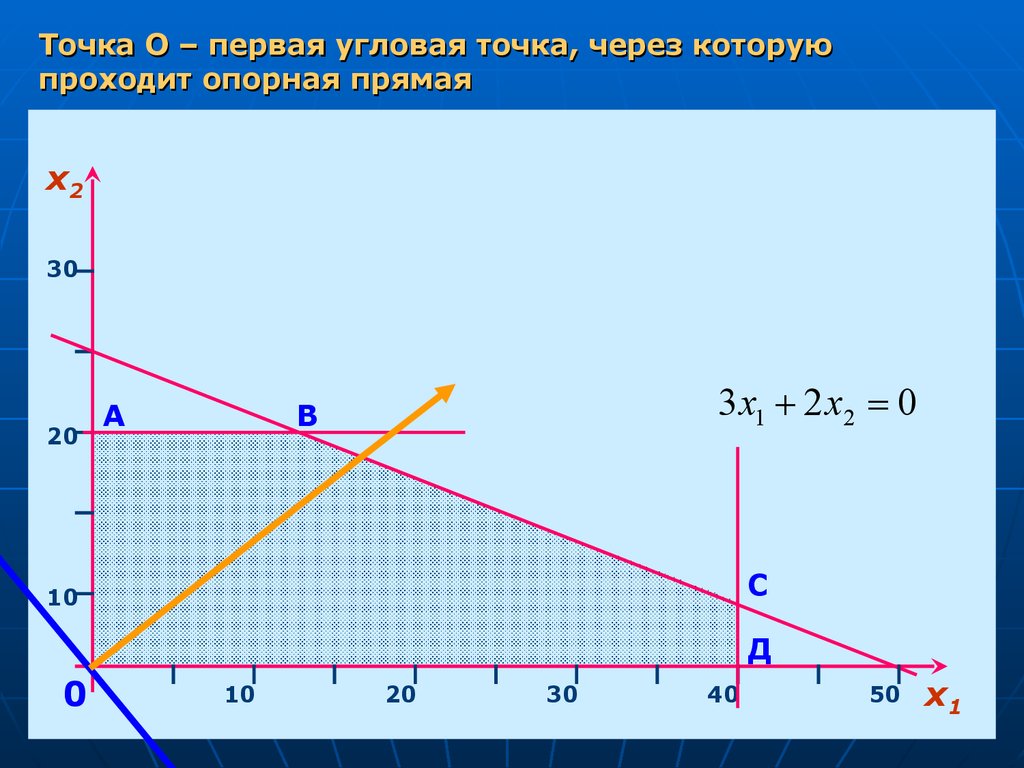
Точка О – первая угловая точка, через которуюпроходит опорная прямая
х2
30
20
А
3 x1 2 x2 0
В
С
10
Д
0
10
20
30
40
50
х1
17.
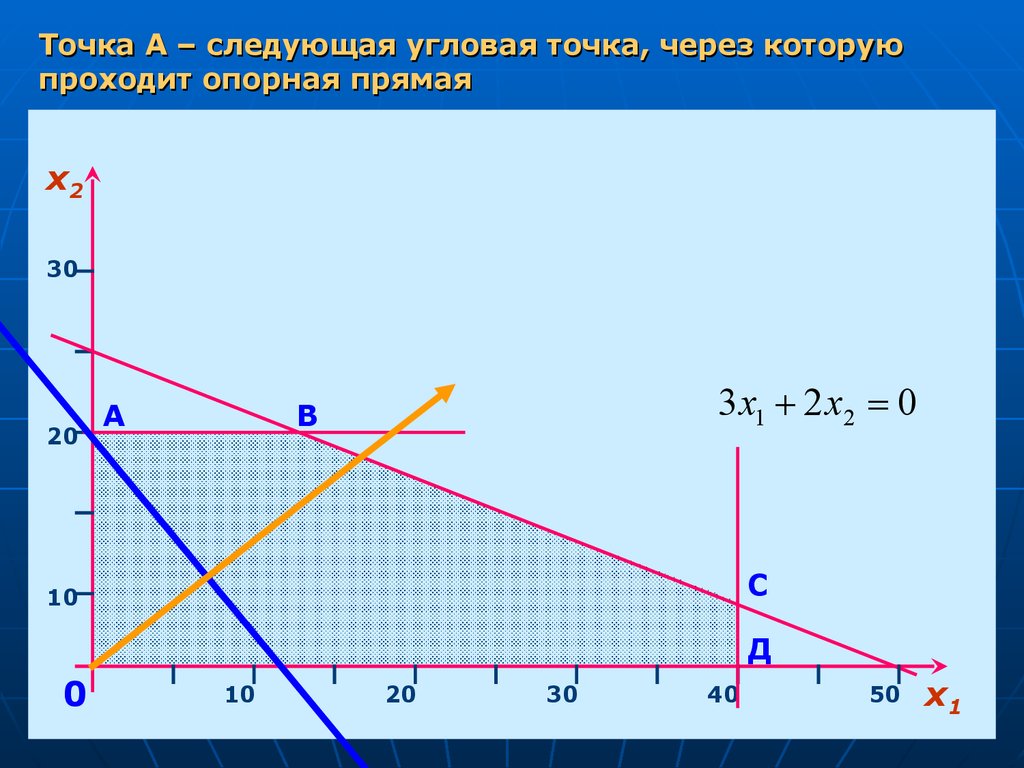
Точка А – следующая угловая точка, через которуюпроходит опорная прямая
х2
30
20
А
3 x1 2 x2 0
В
С
10
Д
0
10
20
30
40
50
х1
18.
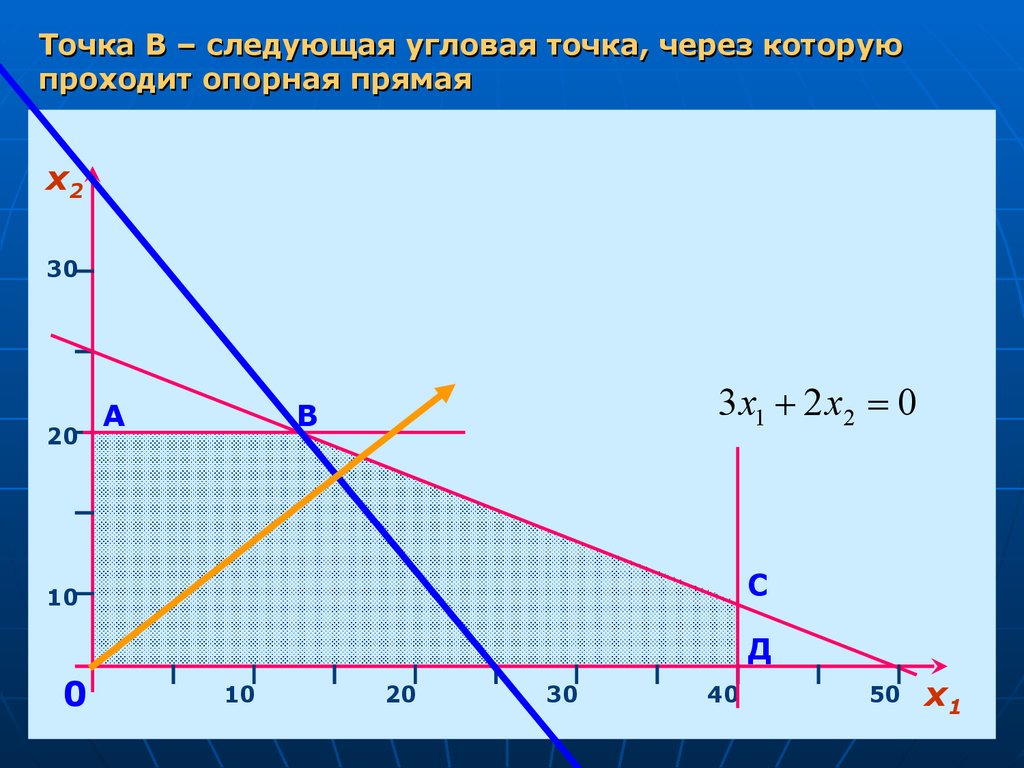
Точка В – следующая угловая точка, через которуюпроходит опорная прямая
х2
30
20
А
3 x1 2 x2 0
В
С
10
Д
0
10
20
30
40
50
х1
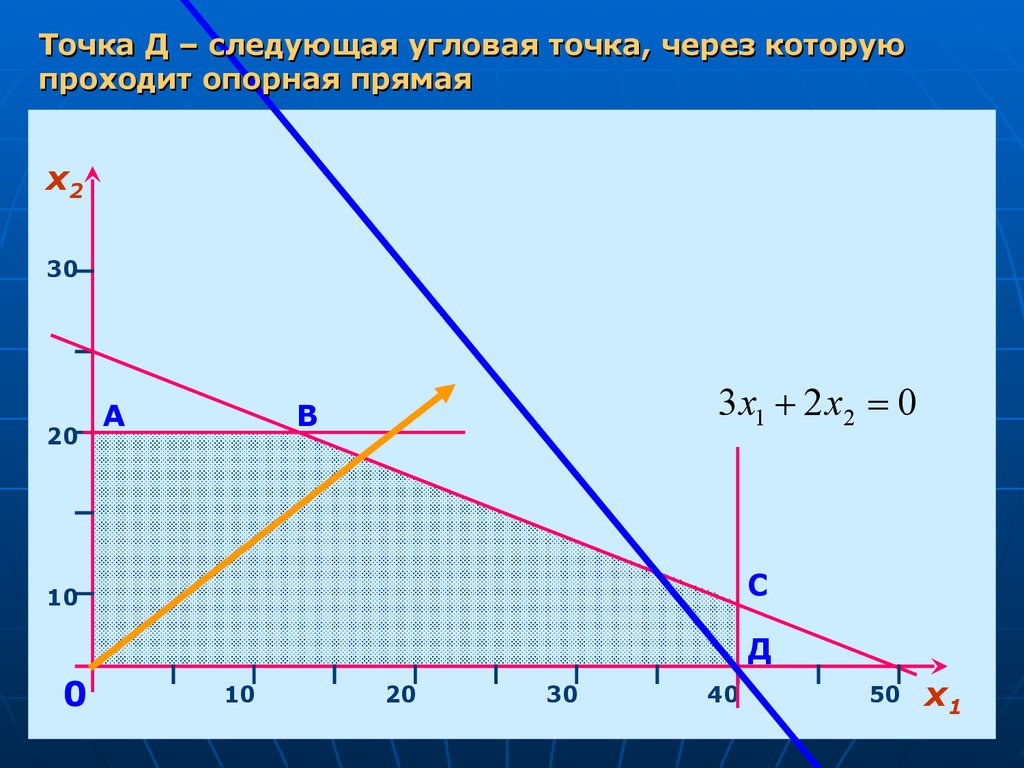
19.
Точка Д – следующая угловая точка, через которуюпроходит опорная прямая
х2
30
20
А
3 x1 2 x2 0
В
С
10
Д
0
10
20
30
40
50
х1
20.
Точка С – последняя угловая точка, через которуюпроходит опорная прямая
х2
30
20
А
3 x1 2 x2 0
В
С
10
Д
0
10
20
30
40
50
х1
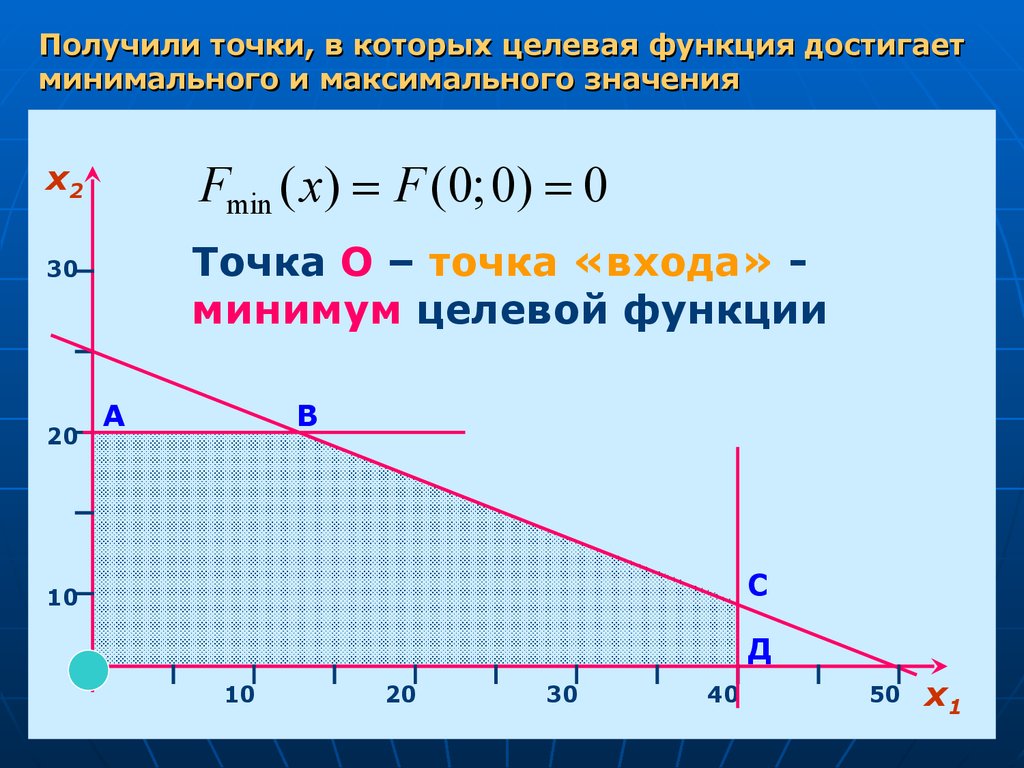
21.
Получили точки, в которых целевая функция достигаетминимального и максимального значения
Fmin ( x) F (0; 0) 0
х2
Точка О – точка «входа» минимум целевой функции
30
20
А
В
С
10
Д
10
20
30
40
50
х1
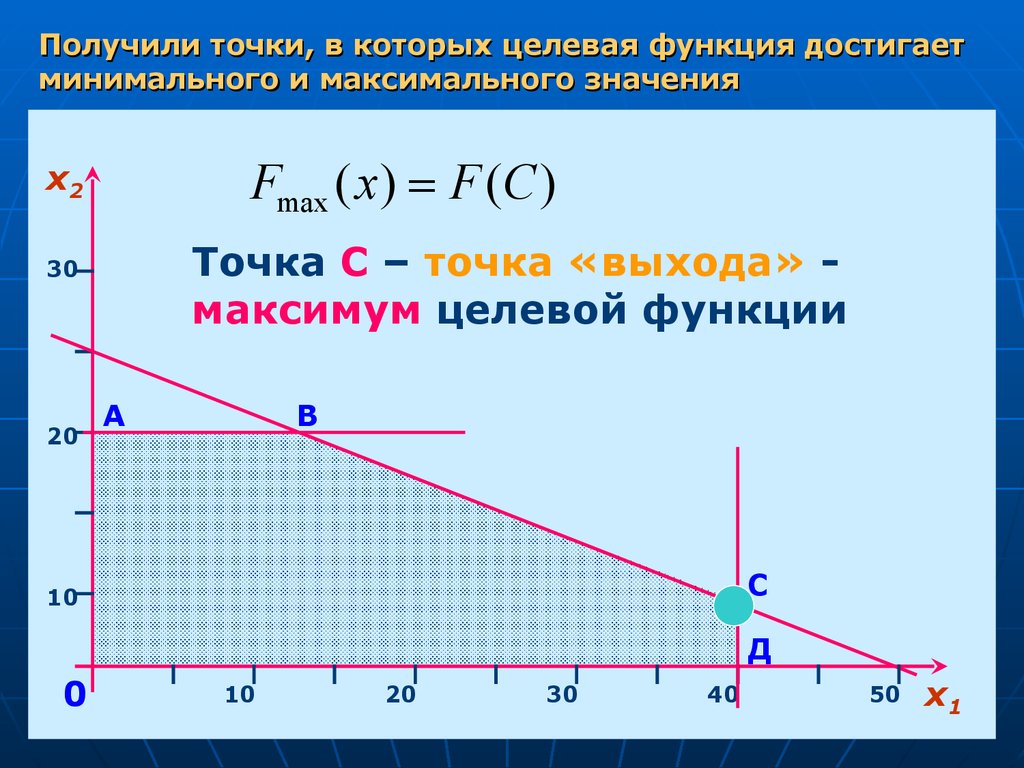
22.
Получили точки, в которых целевая функция достигаетминимального и максимального значения
Fmax ( x) F (C )
х2
Точка С – точка «выхода» максимум целевой функции
30
20
А
В
С
10
Д
0
10
20
30
40
50
х1
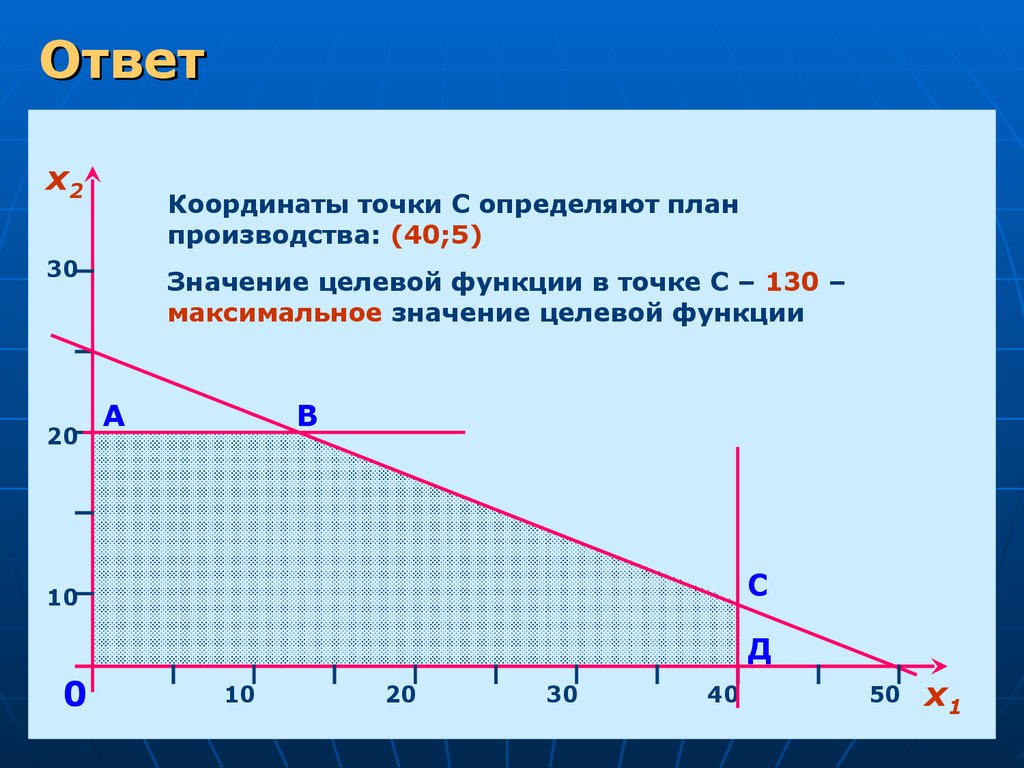
23.
Ответх2
Координаты точки С определяют план
производства: (40;5)
30
20
Значение целевой функции в точке С – 130 –
максимальное значение целевой функции
А
В
С
10
Д
0
10
20
30
40
50
х1







 Математика
Математика








