Похожие презентации:
Излучение возбуждённых поверхностей. Антенно-фидерные устройства и распространение радиоволн
1.
Антенно-фидерные устройства ираспространение радиоволн
ОСНОВЫ ТЕОРИИ АНТЕНН
ЛЕКЦИЯ № 5
ИЗЛУЧЕНИЕ ВОЗБУЖДЁННЫХ
ПОВЕРХНОСТЕЙ
2.
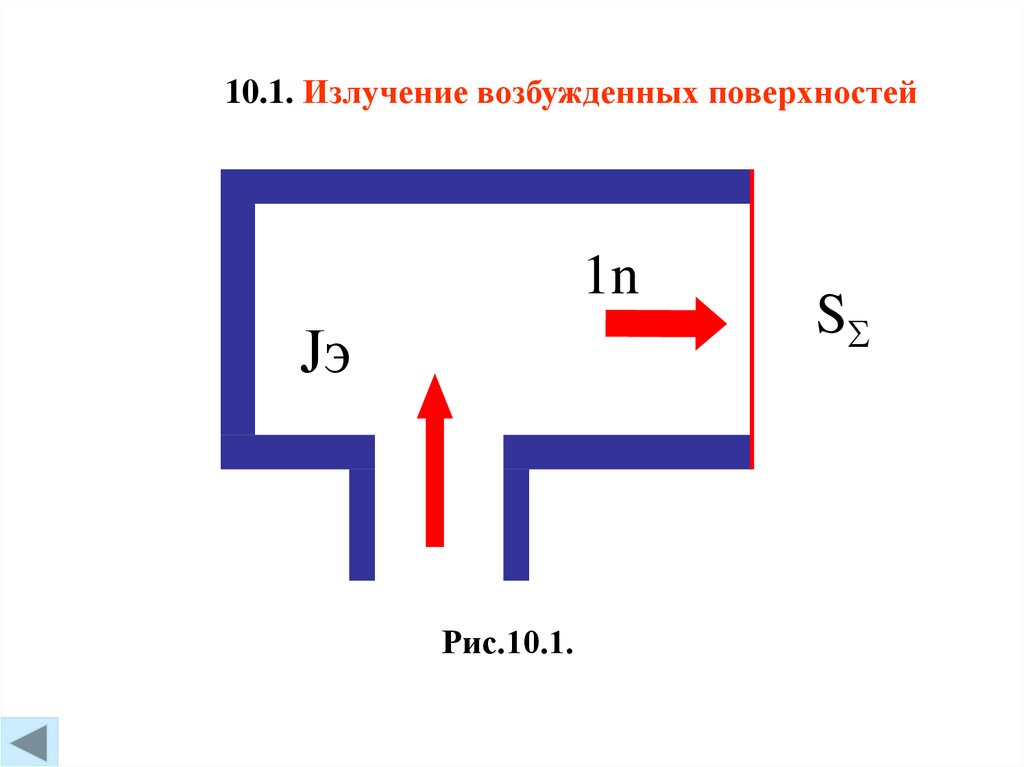
10.1. Излучение возбужденных поверхностей1n
Jэ
Рис.10.1.
S
3.
1) Излучение открытого конца волновода.2) Излучение рупорных антенн.
3) Излучение линзовых антенн.
4) Излучение зеркальных антенн.
Плотность поверхностного электрического тока:
э
J =[1n,H]
Плотность поверхностного магнитного тока:
М
J =-[1n,E]
4.
Поле, создаваемое элементом Гюйгенсадальней зоне (часть плоского волнового фронта):
dE i
E y dxdy
2rO
1 Cos e
ikr
в
(10.1)
Поле на возбуждённой поверхности зададим:
E=ESOf(x,y)ei (x,y)=ESei (x,y)
(10.2)
ES - комплексная амплитуда возбуждающего
поля; ESO - амплитуда возбуждающего поля в центре
раскрыва; f(x,y) - функция, характеризующая
зависимость
амплитуды
поля
от
координат
(амплитудное распределение); (x,y) - фазовое
распределение.
5.
Амплитудное распределение:f(x,y)=f(x)f(y)
Поле, создаваемое элементом Гюйгенса,
расположенного в произвольной точке поверхности:
ESO
i ( x , y )
dE i
f ( x ) f ( y )e
*
2 r
ik r ikr
e
* (1 Cos ) dxdye
6.
Mz
r
P
Ey
а
Hx
Q(x,y)
o
y
b
x
Рис. 10.2
7.
1RO = 1XO Cos Sin + 1YO Sin Sin + 1ZO CosРасстояние из начала координат в точку излучения:
OQ = 1XOx + 1Yoy
Разность хода:
r = xCos Sin + ySin Sin (10.4)
8.
Тогда:*
ESO
i ( x , y )
dE i
f ( x ) f ( y )e
*
2 r
* (1 Cos )dxdy *
ik
(
xCos
Sin
ySin
Sin
)
ikr
e
e
(10.5)
9.
Суммарное поле, создаваемое поверхностью:a/2 b/2
ESO
ikr
i ( x , y )
E i
(1 Cos )e f ( x) f ( y )e
*
2 r
a / 2 b / 2
*
e
ik ( xCos Sin ySin Sin )
dxdy
(10.6)
Для вычисления интеграла рассмотрим частный случай:
Синфазное
равноамплитудное
возбуждение
поверхности (т. е. идеальная плоская антенна):
f(x) = f(y) = 1, (x,y) = 0
10.
Ea
i
ES0
2 r
( 1 Cos ( ) ) e
i k r
b
2
a
2
2
i k r x Cos Cos y Sin Sin
e
dx dy
b
2
ESO ab
E i
(1 Cos )
2 r
ka
kb
Sin
Sin Cos Sin Sin Sin
2
2
e ikr
(10.8)
ka
kb
Sin
Cos
Sin
Sin
2
2
11.
Введём обозначение:u = (kaSin Cos )/2
v = (kbSin Sin )/2
Emax
ab
Eso
r
12.
Нормированная диаграмма направленности:1 Cos Sinu Sinv
F ( , )
2
u
v
(10.9)
ДН поверхности определяется в основном
множителями Sin(u)/u, Sin(v)/v. Они максимальны когда
u = 0, v = 0 т. е. когда = 0. Направление максимумов
множителей системы и диаграммы направленности
элемента Гюйгенса совпадают, поэтому данная
поверхность излучает с максимальной интенсивностью
в направлении нормали.
13.
(1 + Сos( )) - определяет однонаправленные свойстваизлучающей поверхности.
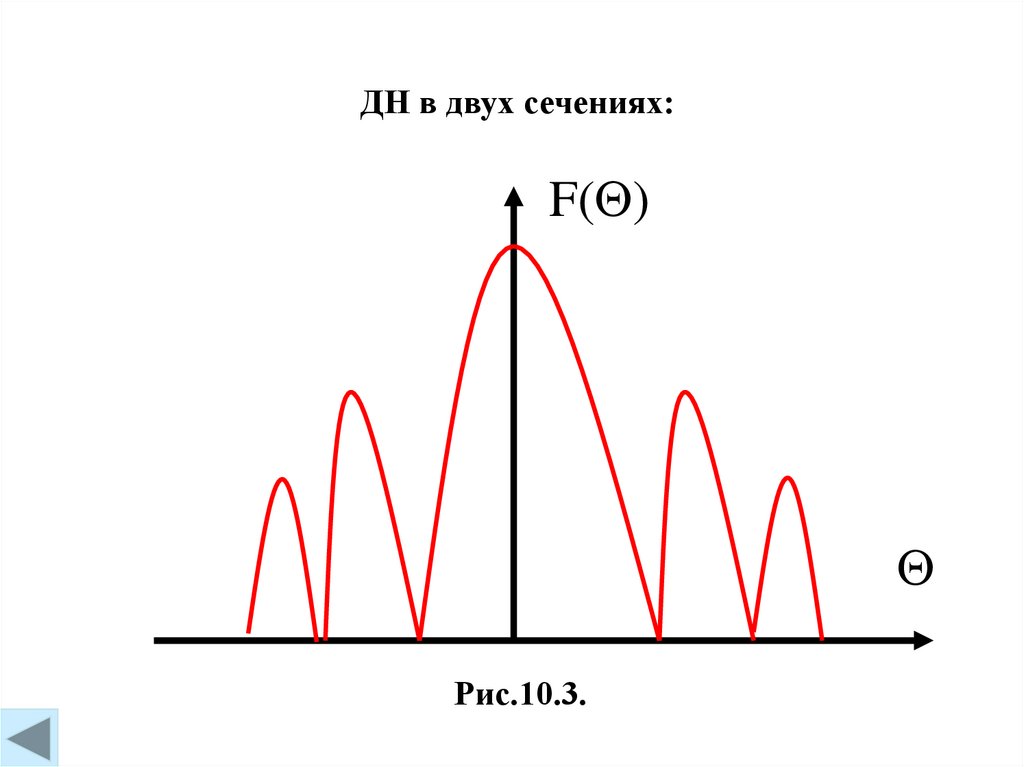
Рассмотрим ДН в двух главных плоскостях:
1) = 0 - плоскость XZ - (плоскость вектора H).
2) = /2 - плоскость YZ - (плоскость вектора E).
14.
ДН в двух сечениях:F( )
Рис.10.3.
15.
Направления нулевого излучения в плоскостях E и H:E
kbSin O =
2N ,
N=1, 2, 3, ...
H
kaSin O = 2N .
Направления первого нуля в плоскостях E и H:
E
Sin 01= /b,
H
Sin 01= /a
16.
Ширина ДН по половинной мощности:E
0
2 0.5=51 /b,
H
2
0.5
0
=51 /a.
17.
1) Т. о. ДН в данной плоскости тем уже, чем большеразмер антенны в этой плоскости.
2) Ширина ДН в данной плоскости не зависит от
размера антенны в ортогональной плоскости.
Уровень первого бокового лепестка:
1
13.3( дБ)
18.
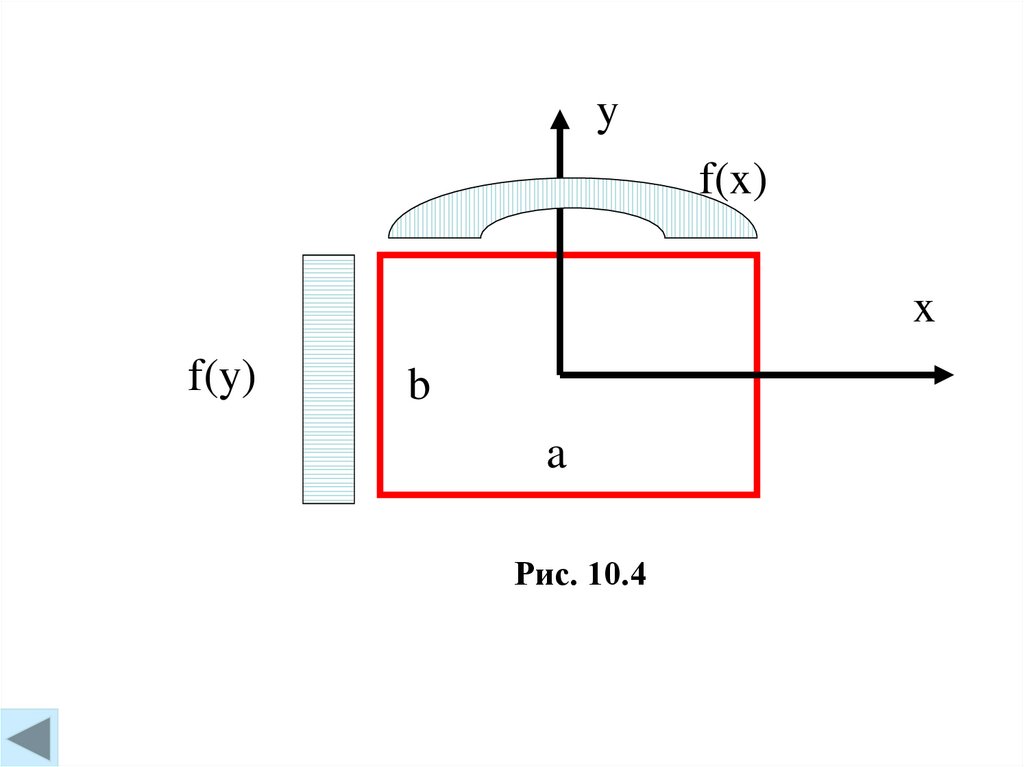
Неравноамплитудное возбуждение поверхности.f(x) = ESOCos( x/a),
= 0 (плоскость Н),
f(y) = 1, (x,y) = 0
19.
yf(x)
x
f(y)
b
a
Рис. 10.4
20.
Тогда, поле излучения в плоскости = 0 :ESO
H
ikr
E i
(1 Cos )e *
2 r
a/2 b/2
x ikxSin H
Cos
(
)
e
dxdy
*
a
a / 2 b / 2
(10.10)
21.
Т. о.:ESO ab
H
E i
(1 Cos ) *
4 r
ka
H
Cos Sin
2
e ikr
*
2
2
ka
H
Sin
2 2
(10.11)
22.
H=0;Emax=2ESOab/( r ).
Нормированная диаграмма направленности:
F ( )
H
*
2
(1 Cos ) *
H
2
ka
H
Cos Sin
2
ka
H
Sin
2 2
2
2
(10.12)
23.
Первый боковой минимум:E
kaSin O/2
= /2
Второй минимум:
E
kaSin O/2
= 3 /2
Первое направление нулевого излучения:
H
Sin
=
3 /a
O
24.
10.2. КНД излучающей поверхности:2
2
max
r E
60 P
Dmax
(10.13)
Вектор Пойнтинга:
Es
П
2
2Wc
E
2
SO
f ( x) f ( y )
2
2Wc
(10.14)
25.
Мощность излучения:2
ESO
P
2WC
2
2
f ( x) f ( y) dS
S
Максимальная напряжённость поля в дальней зоне:
2
Emax
2
ESO
2
(r )
f ( x ) f ( y )e
S
i ( x , y )
dS
2
(10.15)
26.
КНД:2
D
4
2
f ( x ) f ( y )e
i ( x , y )
dS
s
S
2
2
f ( x) f ( y ) dS
27.
Рассмотрим частный случай:4 S Д
1)
D
2
(x,y)=0
f(x)=f(y)=1
Do
4 S
2
4 ab
2
28.
2)f(x)=Cos( x/a),
a/2 b/2
D
4
2
Cos
Cos
a / 2 b / 2
2
x
dxdy
a
a / 2 b / 2
a/2 b/2
2
f(y)=1, (x,y)=0
x
a
0.81
dxdy
4
2
S 0.81DO
Коэффициент использования поверхности:
SД
S
0.81



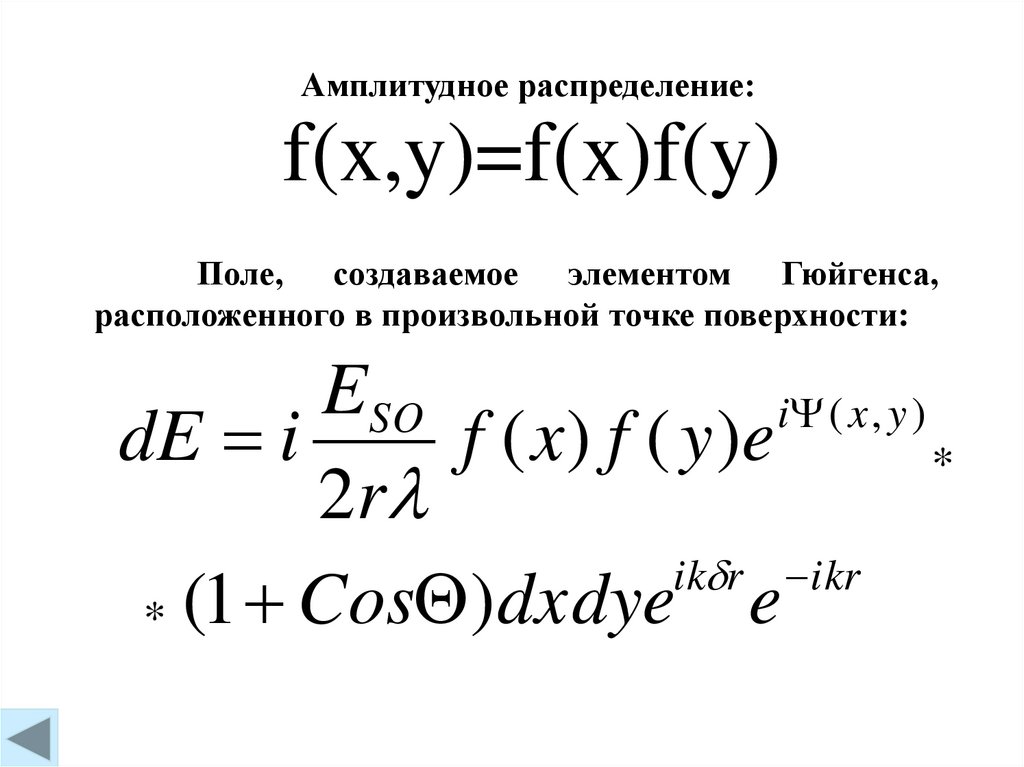

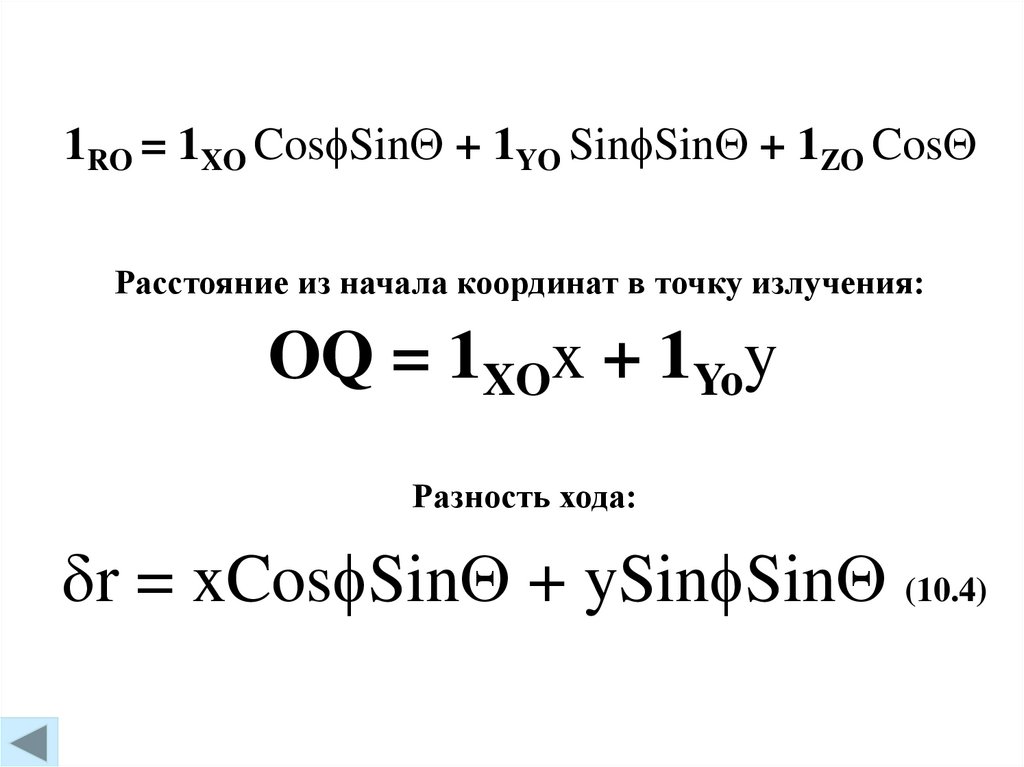


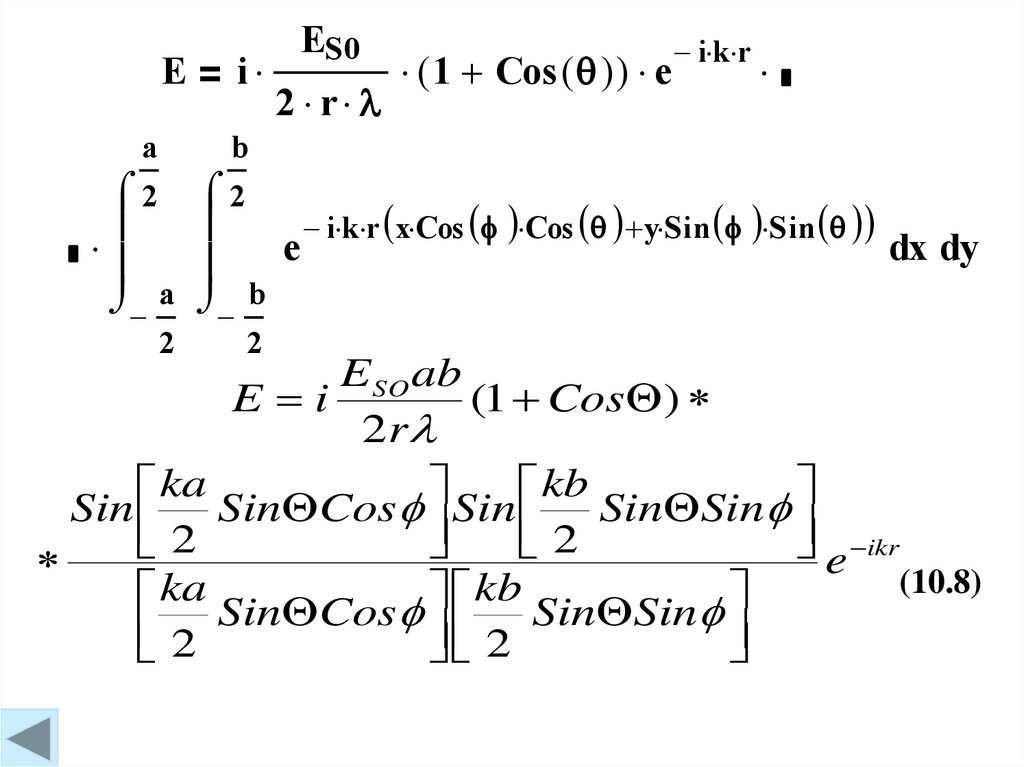







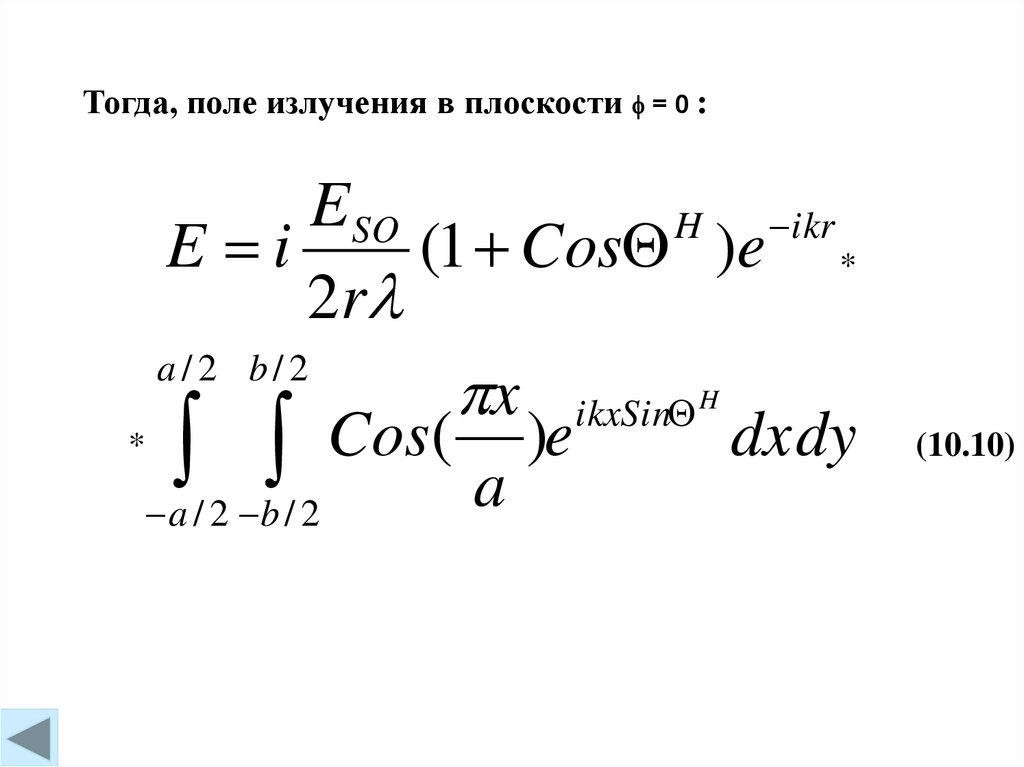
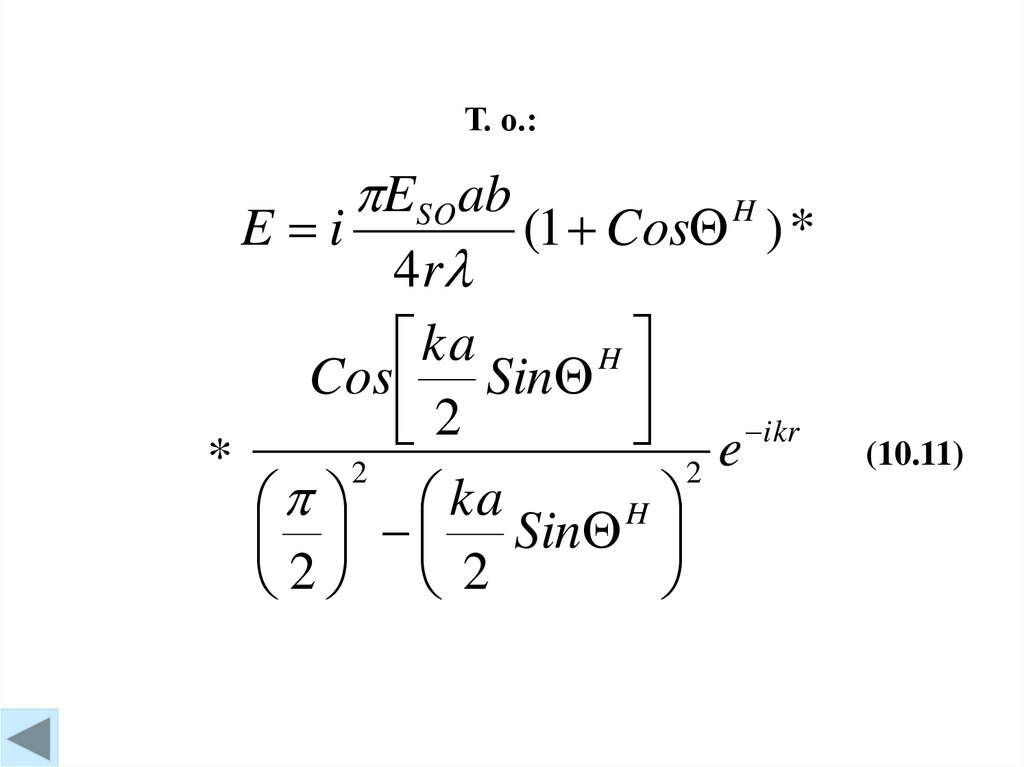




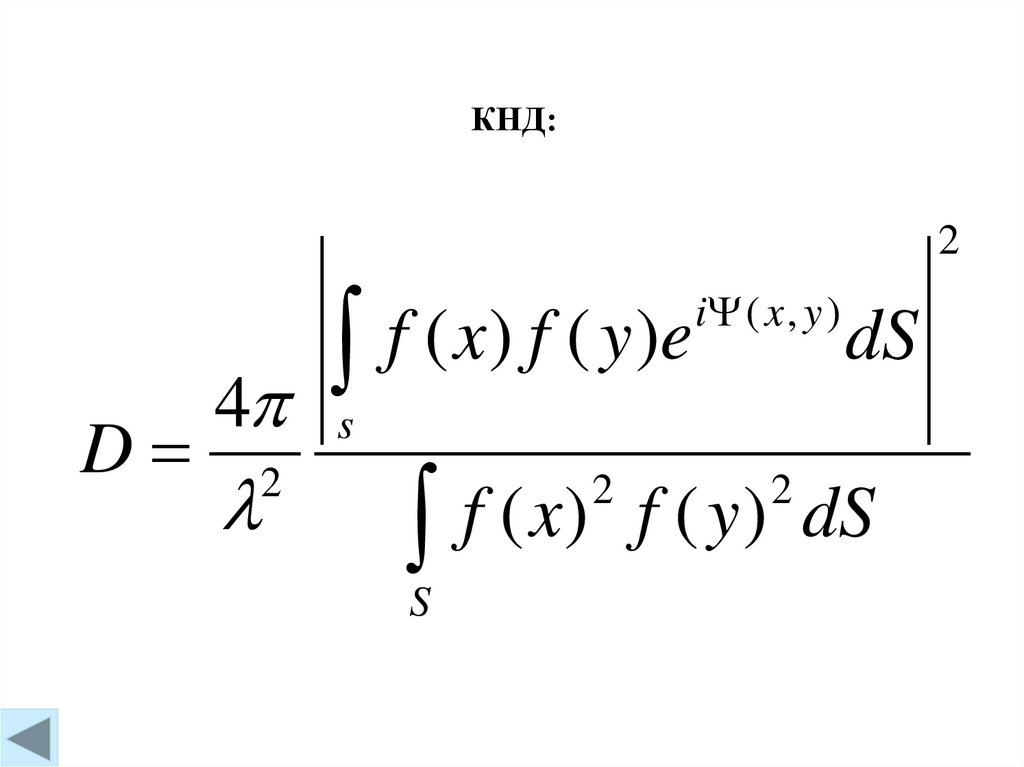


 Физика
Физика








