Похожие презентации:
Моделирование конфликтных ситуаций с применением математической теории игр
1.
Моделирование конфликтныхситуаций с применением
математической теории игр
2. Теория игр
1. Основные понятия теории игр.Теория игр Конфликтная ситуация
Черты конфликтной ситуации:
Игра Игроки Стратегии игроков –
Правила –
• Выигрыш или платеж игры • Платежная матрица
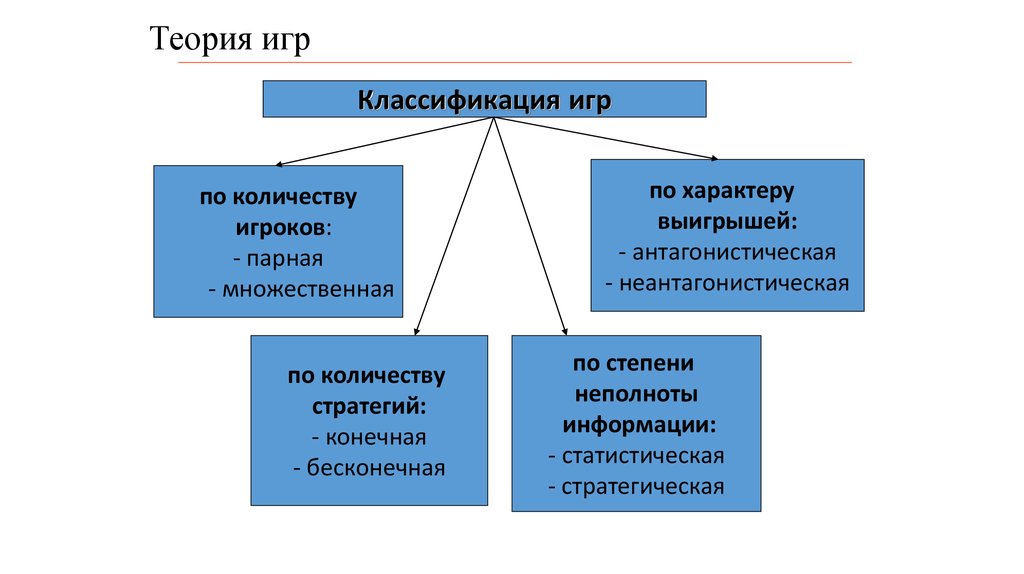
3. Теория игр
Классификация игрпо количеству
игроков:
- парная
- множественная
по количеству
стратегий:
- конечная
- бесконечная
по характеру
выигрышей:
- антагонистическая
- неантагонистическая
по степени
неполноты
информации:
- статистическая
- стратегическая
4. Теория игр
2. Постановка парнойантагонистической игры.
Дано:
A1,A2,…,Am - стратегии игрока А (чистые
стратегии игрока А);
B1,B2,…,Bn- стратегии игрока В (чистые
стратегии игрока А).
aij (i= 1, m ; j= 1, n ) – платеж игрока В, при
выборе им j – ой стратегии, игроку А, если
последний выбирает свою i – ю стратегию.
Найти решение игры
5. Теория игр
• Платежная матрица:a11
a 21
...
Р
ai1
...
a
m1
a12
... a1 j
a 22
... a 2 j
...
...
...
ai 2
...
aij
...
...
...
am2
... a mj
... a1n
... a 2 n
... ...
... ain
... ...
... a mn
6. Теория игр
• Цель теории игр –• Решить игру –
• Оптимальными
Цель игрока А – получить максимальный
гарантированный выигрыш при наихудших
условиях.
Цель игрока В – уменьшить выигрыш игрока А.
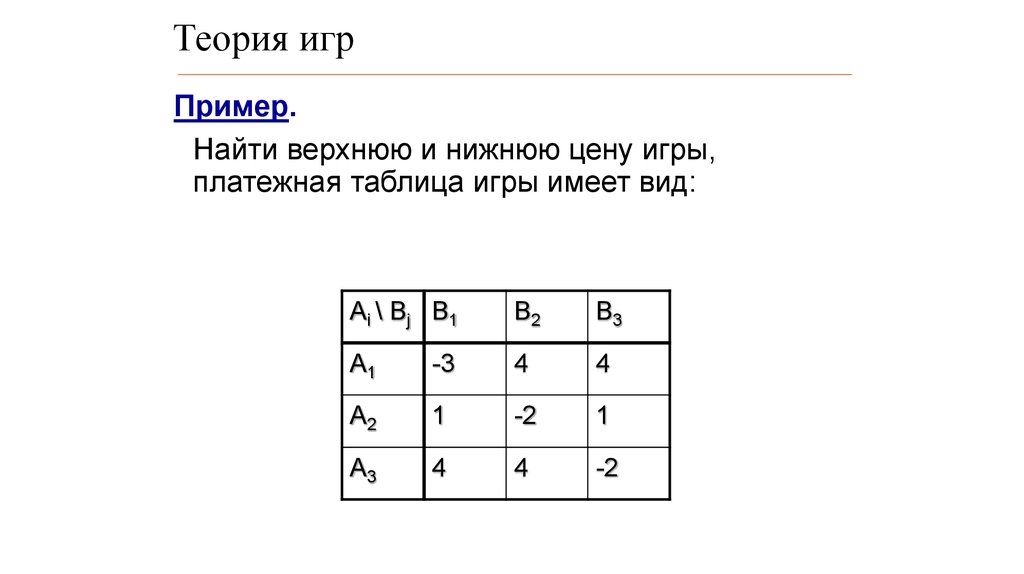
7. Теория игр
Пример.Найти верхнюю и нижнюю цену игры,
платежная таблица игры имеет вид:
Ai \ Bj B1
B2
B3
A1
-3
4
4
A2
1
-2
1
A3
4
4
-2
8. Теория игр
4. Принцип доминирования.Цель - уменьшить размерность задачи
(редуцировать платежную матрицу).
Принцип доминирования – один из приемов
редуцирования платежной матрицы.
Идея принципа – исключить из рассмотрения те
стратегии игроков, которые являются очевидно не
выгодными для игроков.
9. Теория игр
5. Решение игры в чистых стратегиях.Если α = β, то игра имеет седловую точку (или
седловые точки).
Решение игры сводится к нахождению седловой
точки.
Цена игры с седловой точкой равна: υ =α = β.
Пример. Проверить имеет ли игра седловую точку:
0,7 0,5 0,3
Р
0,6 0,9 0,4
10. Моделирование конфликтных ситуаций в экономике
Матричные игры и задачи линейногопрограммирования.
Между матричными играми и линейным
программированием существует взаимосвязь, которая
состоит в том, что решение любой матричной игры
можно свести к решению пары двойственных задач
линейного программирования специального вида и,
наоборот, любая задача линейного программирования,
которая имеет решение, может быть сведена к
матричной игре специального вида.
11. Моделирование конфликтных ситуаций в экономике
Вводя переменные x1=p1/v, x2=p2/v,… и, учитывая, что игрок А стремитсяполучить максимальный выигрыш (V=>max или 1/v=>min), получим
задачу линейного программирования для игрока А: (Аналогичные
рассуждения приводят к двойственной задачи для игрока В)
Z=x1+x2+x3+…+xm=>min
a11x1+a21x2+…+am1xm ≥ 1
a12x1+a22x2+…+am2xm ≥ 1
F=y1+y2+y3+…+yn=>max
a11y1+a12y2+…+a1nyn ≤ 1
a21y1+a22y2+…+a2nyn ≤ 1
a1nx1+a2nx2+…+amnxm ≥ 1
am1y1+am2y2+…+amnyn ≤ 1
Решения этих задач позволяет найти оптимальные смешанные
стратегии игроков А и В.
12. Моделирование конфликтных ситуаций в экономике
Пример. Пусть исходная матрица игры имеет вид.А\В
В1
В2
В3
αi
А\В
В1
В2
В3
αi
А1
-3
4
4
-3
А1
1
8
8
1
А2
1
-2
1
-2
А2
5
2
5
2
А3
4
4
-2
-2
А3
8
8
2
2
βj
4
4
4
4\-2
βj
8
8
8
8\2
Задачи линейного программирования для игроков А и В имеют вид:
Z= Х1+х2+х3 => min F=y1+y2+y3=>max
Решение есть:
1x1+5x2+8x3 ≥ 1 1y1+8y2+8y3≤ 1
Z=0.2045; V1=1/z=4.89; V=V1-4=0.89
8x1+2x2+8x3 ≥ 1 5y1+2y2+5y3≤ 1
x1=0.045; x2=0.106; x3=0.053;
8x1+5x2+2x3 ≥ 1 8y1+8y2+2y3≤ 1
p1=0.222; p2=0.519; p3=0.259;
q1=0.444; q2=0.037; q3=0.519










 Математика
Математика








